改進的LeNet-5模型在花卉識別中的應用

吳麗娜，王林山

(中國海洋大學 數學科學學院，山東 青島 266100)

0 引 言

卷積神經網絡模型是一種具有高學習效率，非線性映射能力以及較強的魯棒性和容錯性的深度學習模型[1,2]，因此該網絡被廣泛關注，它的理論和應用研究是人工神經網絡領域的熱點之一。

卷積神經網絡有多種形式，如，在海量圖像分類領域取得突破性成果的Alex Net模型[3]；適用于目標檢測的R-CNN(regions with CNN)[4]模型；能夠實現端到端的圖像語義分割的全卷積網絡(fully convolution networks，FCN)模型[5]，應用于圖像的摘要生成和圖像內容問答的RNN[6,7]模型。尤其是應用于手寫字符識別、圖像分類的LeNet-5卷積神經網絡模型，是由LeCun提出的一種典型的用來識別手寫數字的卷積神經網絡模型[8]，在計算機視覺領域有廣泛的應用和改進：如，李勇等[9]用了跨連接的思想, 提出一種新的LeNet-5卷積神經網絡模型，將其用于面部表情識別，并在JAFFE表情公開庫和CK+數據庫取得了較好的識別效果；馬苗等[10]去掉基本LeNet-5中的第3卷積層,并用SVM分類器代替輸出層中的Softmax分類器，在國際公開的SVHN數據集的實驗結果表明，改進的LeNet-5對街景門牌號碼的識別效果較好，并達到了較高的識別率；特別是劉德建等[11]成功地應用經典LeNet-5卷積神經網絡成功地研究花卉識別問題，存在著進一步提高花卉圖像識別率的問題。本文在文獻[11]的基礎上，試圖對LeNet-5卷積神經網絡進行改進，并對Oxford-17(17 category flower datasets)花卉數據集進行測試，實驗結果表明，改進的LeNet-5卷積神經網絡對花卉圖像的識別率達到96.5%，比未改進的LeNet-5卷積網絡提高了6.5%。

1 LeNet-5卷積網絡模型

LeNet-5卷積網絡模型(如圖1所示)不包括輸入層，總共有7層，包括：C1卷積層，S2池化層，C3卷積層，S4池化層，C5卷積層，F6全連接層，Output輸出層。輸入的圖像是32×32像素的圖像。C1卷積層有6張特征圖，其運算方式是每個特征圖中的每個單位都與輸入圖中的 5×5 像素的區域相連，且每個特征圖都通過6個5×5像素大小的卷積核進行卷積操作，從而得到6個28×28像素大小的特征圖。S2池化層包括6張特征圖，與C1卷積層中的特征圖數目相等，該層每張特征圖的大小為14×14像素,其運算方式是每個特征圖的單元都與C1卷積層中的每個特征圖的2×2像素的區域相連。C3卷積層有16張特征圖，其運算方式是每個特征圖都通過5×5像素的卷積核與S2池化層中的某幾個或全部特征圖進行卷積操作得到，見表1。S4池化層共有16個5×5像素大小的特征圖，其運算方式是該層特征圖的每個單元都與C3層每個特征圖的 2×2 像素區域相連。C5卷積層共有120個特征圖，每個特征圖單元都與S4層所有特征圖5×5像素的區域相連，該層的特征圖都通過5×5像素的卷積核與S4層的所有特征圖進行卷積操作得到，所以該層特征圖的大小為1×1像素。F6全連接層共有84個單元, 并且F6層與C5層是全連接的。Output輸出層采用的是歐式徑向基函數(RBF)。

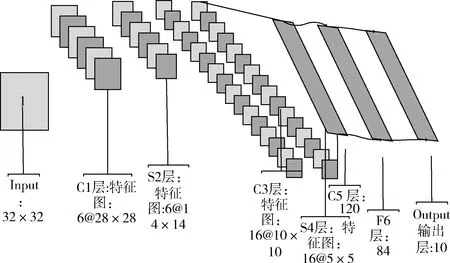
圖1 LeNet-5網絡結構

表1 S2與C3的連接方式

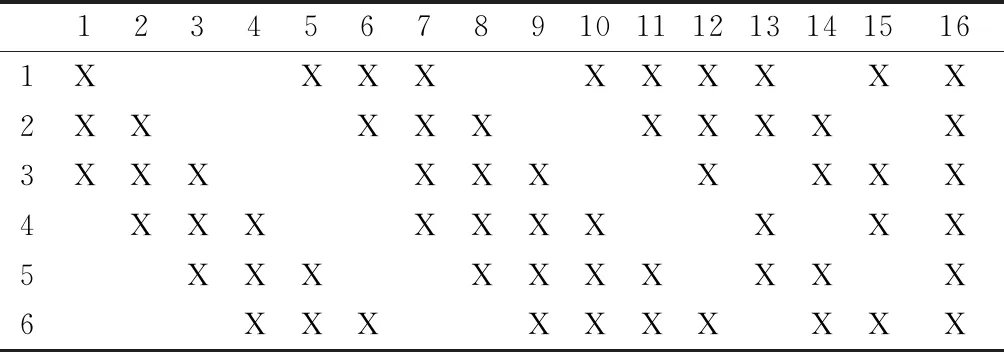
123456789101112131415161XXXXXXXXXX2XXXXXXXXXX3XXXXXXXXXX4XXXXXXXXXX5XXXXXXXXXX6XXXXXXXXXX

2 LeNet-5卷積網絡模型的改進

LeNet-5卷積神經網絡模型最初是通過卷積核自動提取特征，將原始數據通過一系列的非線性變換轉化為高維特征，從而對高維特征進行分類。但是這種分類方法沒有考慮到低維的細節特征，且隨著深度的增加，易出現梯度消失或爆炸問題[12]。為了解決此類問題，使得低維細節特征均勻地傳遞給下一層，并將高維的突出特征全部傳遞給輸出層，本文主要從池化操作方式以及S4層與C5層的連接方式入手，并針對花卉以及花瓣與手寫數字字符存在形態上的差異，在不考慮同一類別的花卉有很大的差異性以及圖像背景復雜的前提下[13]，對原LeNet-5卷積神經網絡模型進行如下改進和與文獻[11]不同的參數設置，以此為基礎給出新的訓練算法：

(1)關于池化操作的改進：S2層的池化操作設置為均值池化(Avg-pooling)，且S4層的池化操作設置為最大池化(Max-pooling)；

(2)關于連接方式的改進：將C5層設置為全連接層，即將S4層與C5層之間的5×5卷積核去掉，使兩層的特征圖以全連接的方式相連。

(1)

其中，f為激活函數，bj為偏置向量(bias)，n表示S4層神經元的個數。k表示C5層神經元的個數。圖2為LeNet-5網絡拓撲圖。

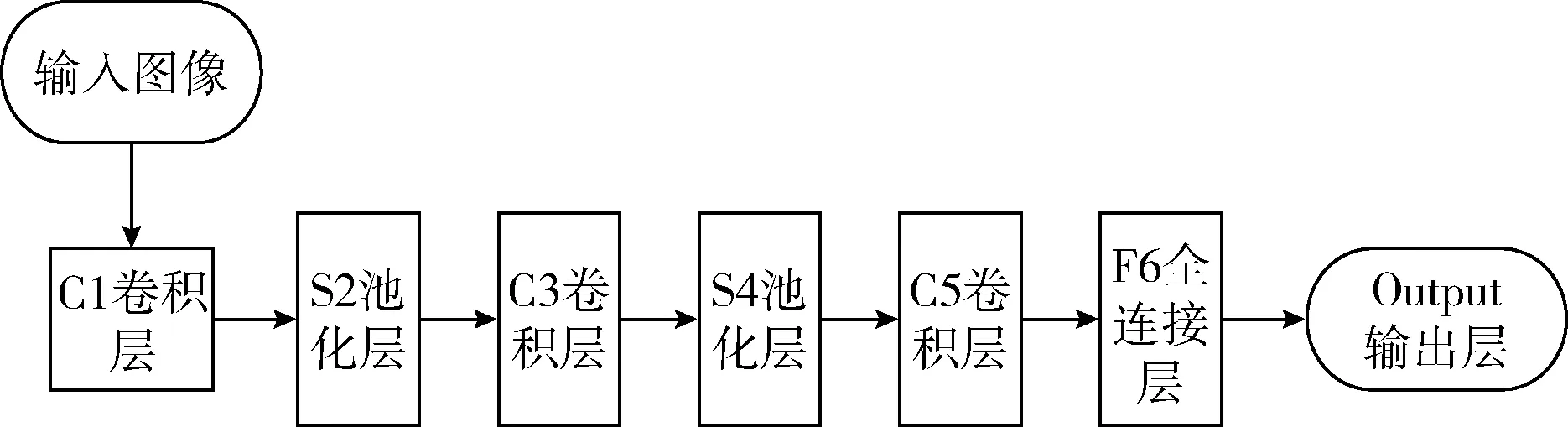
圖2 LeNet-5網絡拓撲

2.1 參數設置

(1)在F6層之后、輸出層之前使用Dropout正則化方法。

(2)將激活函數設置為ReLU激活函數

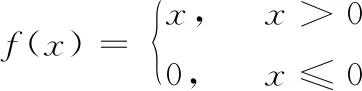
(2)

(3)算法：使用隨機梯度下降算法SGD(stochastic gradient descent)[14]更新權值參數。SGD算法原理公式

(3)

(4)

(5)

其中，h(α) 表示擬合函數，J(α) 表示損失函數，α=(α1,α2,…,αn) 表示網絡參數權值，yi表示第i個樣本的樣本值，m表示的是整個迭代進行的總次數,j表示網絡中參數的總數目，α′j表示更新后的網絡參數。

(4)分類器的確定：選用Softmax分類器。對于Output層,輸入x， 則有

(6)

其中，ω=(ω1,ω2,…,ωm)T表示權值，P計算的是輸入為j類別時的概率，設置輸出類別為17。

2.2 參數設置理由

(1)S2層的均值池化操作，能夠使得上一層中的低層次細節特征可以充分或均勻地出現在下一層的特征圖中。S4層的最大值池化，可以保證C3層中更為突出的高層次特征傳遞給下一層(S4層)。

(2)將C5層設置為全連接層以后，圖像的高維特征通過全連接的方式傳遞給下一層，取得的識別效果更好。

(3)Dropout方法是卷積神經網絡中經典的正則化方法，實驗中數據集并不是非常大，使用Dropout方法能有效減少過擬合現象。

(4)將激活函數替換為ReLU激活函數。使用傳統的Sigmoid激活函數，需要預訓練，否則會出現梯度消失無法收斂的問題。將激活函數替換為ReLU激活函數會使收斂速度更快[15]。

(5)隨機梯度下降算法SGD每次只隨機選擇一個樣本來更新模型參數，因此每次的學習是非常快速的。

(6)由于本次實驗輸出類別數為17，所以選擇Softmax多分類器。

改進后的網絡結構設置見表2，新網絡結構如圖3所示。學習率設置：本文分別考察了學習率為0.001和0.01對識別率的影響，實驗結果表明，在相同條件下，學習率設置為0.001時，識別率更高。因此學習率設置為0.001。

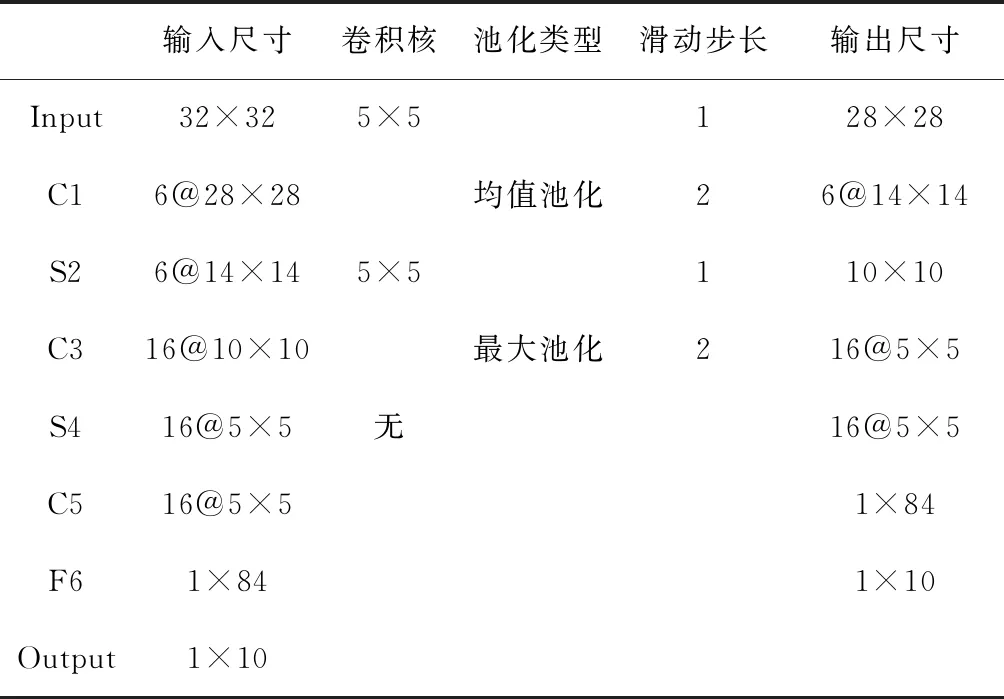
表2 新的LeNet-5網絡結構

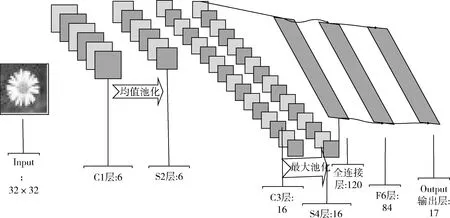
圖3 新的LeNet-5網絡結構

3 基于改進LeNet-5模型的花卉分類問題研究

3.1 數據集的選擇

數據集是包含17個類別的牛津花卉(Oxford-17 flo-wer)數據集，該數據集是由牛津大學Visual Geometry Group創建的。每個類有80幅圖像，總共有1360張圖像，本文選取其中1000張圖像作為訓練樣本，200張作為測試樣本集。圖4是實驗中部分花卉圖像。

圖4 部分彩色花卉圖像

3.2 圖像預先處理

圖像預處理一般是指對輸入的數字圖像進行顏色空間轉換，高斯濾波等[16]。顏色是花卉圖像最顯著的特征之一，具有形狀和方向無關性，適合作為花卉種類識別的依據[17]。但是顏色會對花卉種類的識別造成一定的干擾，每類花的顏色，拍照時圖像的亮度都對花卉種類的識別產生較大的影響，彩色圖像存儲量大，處理不方便，需要將彩色圖像轉化為包含同樣信息量且處理過程更加簡單快速的灰度圖像[18,19]。

使用matlabR2016將收集到的圖像進行預處理：先將所有圖像統一轉化為單通道的灰度圖像, 灰度級設置為8，并對數據集進行批量人工標號。其次，將圖像的分辨率統一轉化為28×28大小的分辨率，最后使用VS2013和Opencv3.1將圖像轉化為相應的二進制格式文件。圖5～圖7 表示部分灰度圖像、向日葵放大灰度圖像和識別錯誤圖像。

圖5 一些灰度圖像

圖6 向日葵的放大灰度

圖7 識別錯誤的圖片

3.3 實驗環境的介紹

硬件環境：

本次實驗是在牛津花卉數據庫上進行的實驗，考慮到數據量不是很高，以及網絡深度并沒有很大，所以實驗數據放在單CPU上進行處理，實驗硬件環境見表3。

軟件安裝及配置：

實驗中所用的深度學習框架是tensorFlow[20]，編程語言是Python3.5.4，輔助軟件工具是matlabR2016，Opencv3.1和VS2013。

tensorFlow是一個非常強大的用來做大規模數值計算

表3 硬件環境

的庫。其所擅長的任務就是實現以及訓練深度神經網絡。它已經在大量移動設備上或者大規模分布式集群中使用，已經經過了實踐檢驗。其分布式實現是基于圖計算，它將圖分割成多個子圖，每個計算實體作為圖中的一個計算節點[21]。本文最終得到的圖表則是應用了tensorboard這一可視化工具。

3.4 實驗步驟

(1)初始化卷積核，偏置向量(bias)。

(2)設置訓練參數，將學習率設置為0.001，批訓練樣本數量batch設置為100，迭代次數epochs=2000，每次訓練batch個樣本數量。每100次迭代輸出一次結果，最后輸出總識別率。

(3)輸入樣本，正向傳播和誤差反向傳播，用SGD更新權值參數。

(4)啟動tensorboard，借助谷歌瀏覽器打開相關網址，將訓練過程可視化。

為了驗證改進后的新模型的可行性，從總樣本中不同種類的花瓣集選取了共100張圖片進行檢驗(即設置validation_size=100)。整個實驗，沒有使用GPU及CUDA加速，在單CPU上的訓練時間是3.5小時左右。

3.5 實驗結果與評價

改進LeNet-5網絡模型部分實驗輸出結果展示：

test Accuracy at step 0:0.16

test Accuracy at step 500:0.64

test Accuracy at step 1000:0.88

test Accuracy at step 1500:0.94

test accuracy 0.965

實驗中，在原LeNet-5網絡模型上進行訓練，訓練到第1000步的時候，識別正確率達到0.88，在迭代到1500步的時候，識別結果達到0.94，總體識別率為0.965，圖8為交叉熵(cross_entropy)變化曲線圖，識別正確率(accuracy_1)變化曲線如圖9所示。

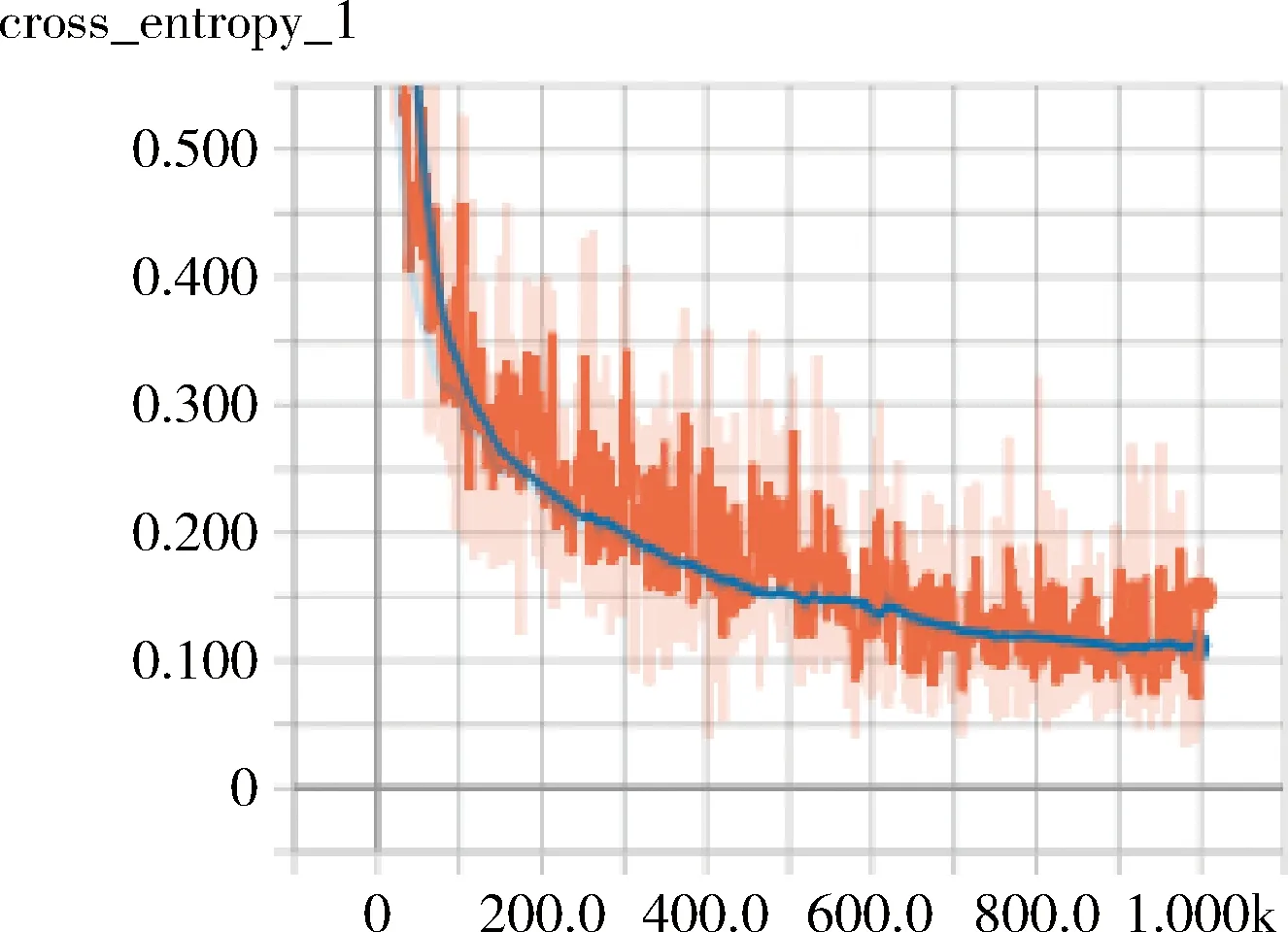
圖8 改進的LeNet-5神經網絡模型交叉熵變化曲線

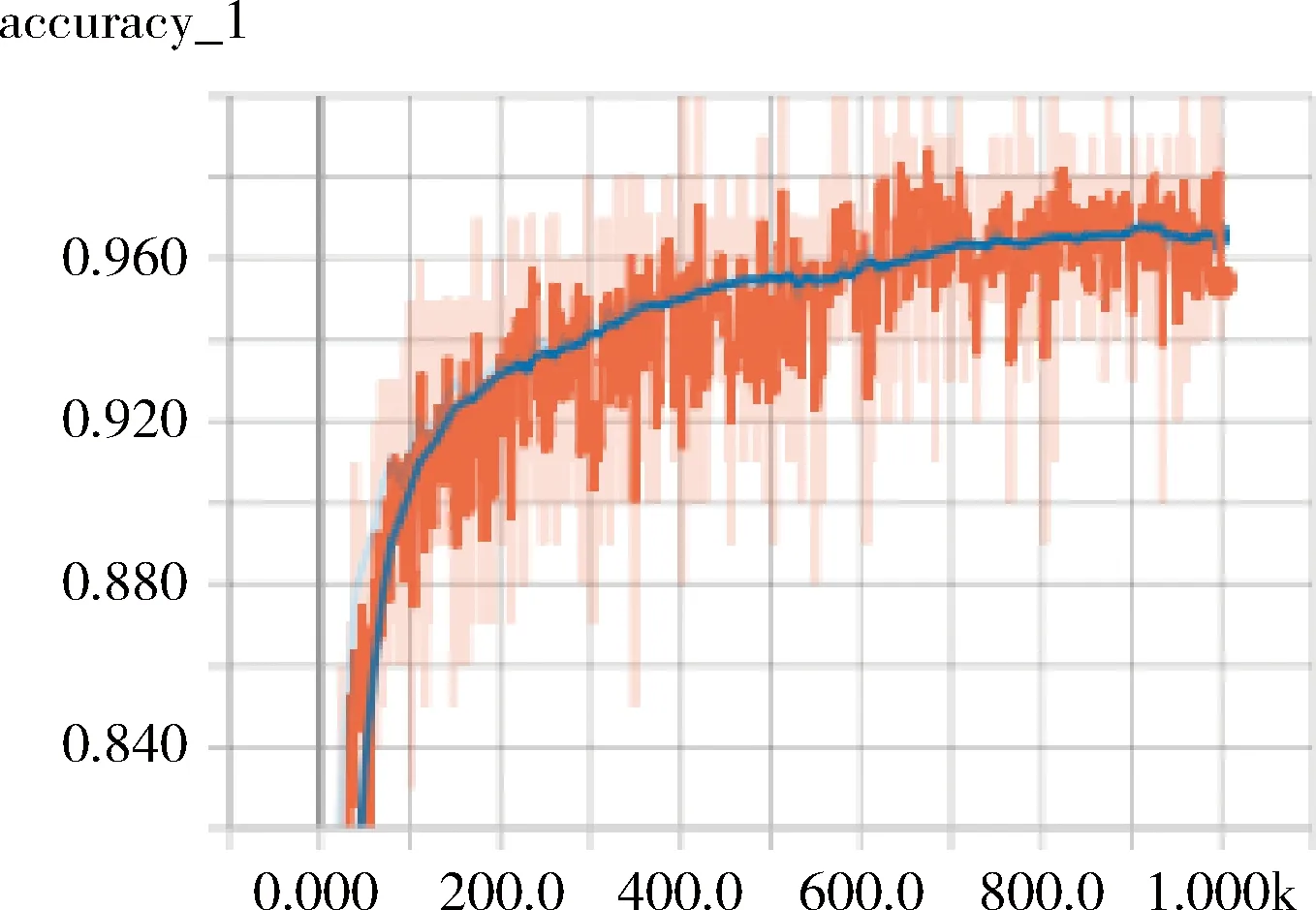
圖9 改進的LeNet-5神經網絡模型 識別正確率變化曲線

對于相同的樣本數據集，每個模型每100步記錄一次結果,總共記錄10次，對比結果如圖10所示,圖10中，橫軸step為迭代步數，縱軸Accuracy為識別正確率。由此結果對比可以得出，改進的LeNet-5卷積神經網絡比BP神經網絡和原LeNet-5卷積神經網絡具有更高的識別精度。

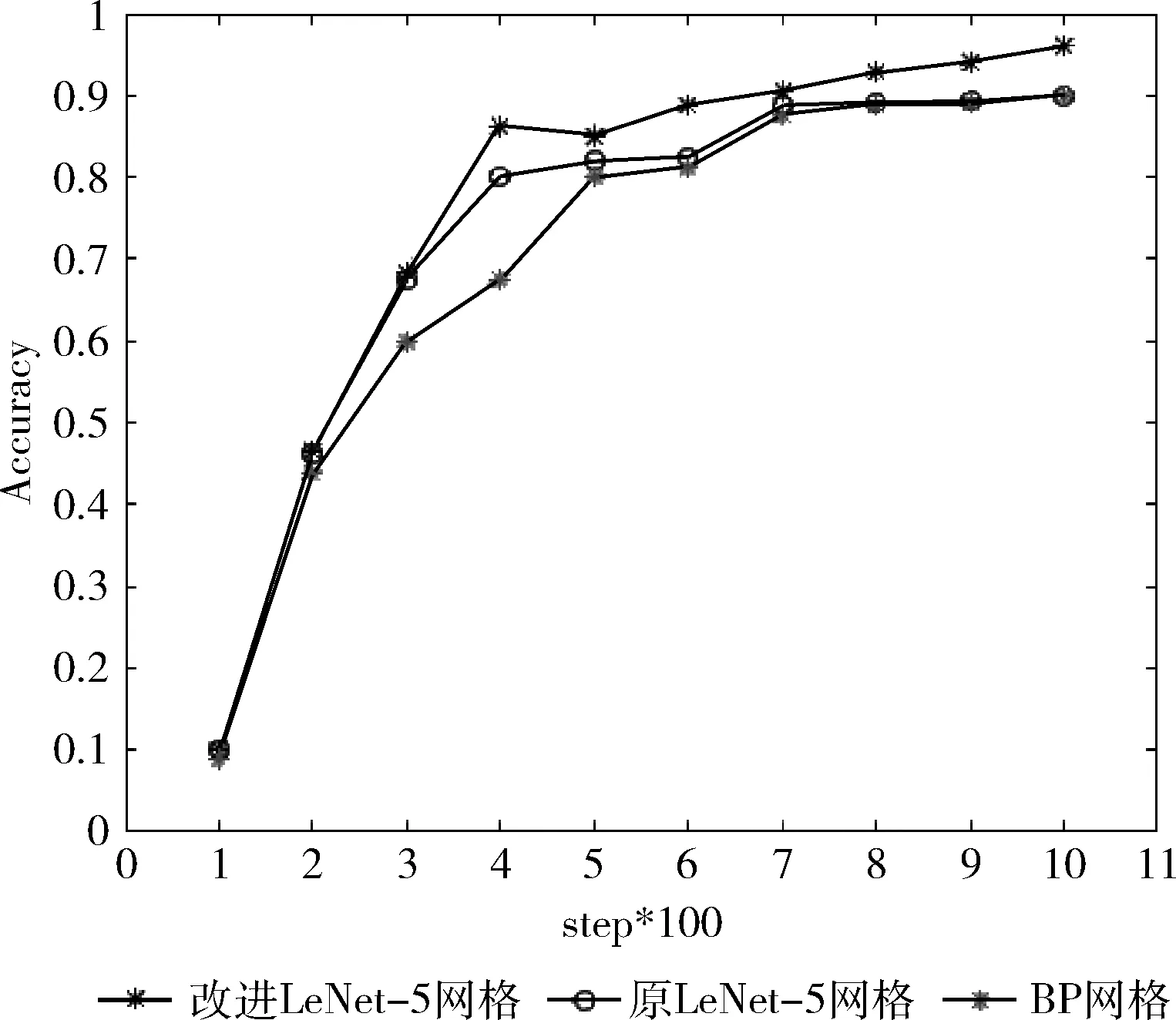
圖10 3種網絡模型對比結果

表4為在新的LeNet-5網絡中，設置不同學習率得到不同的識別率，由此結果可以看出，控制其它參數條件不變，調節學習率這項參數，發現，當學習率設置為0.001時，識別率更高。表5為在新的LeNet-5網絡中其它參數設置不變的情況下，不同激活函數對識別率的影響。表6為在新的LeNet-5網絡中，使用Dropout正則化方法對識別率的影響，顯然，在其它參數設置不變的情況下，有無Dropout對識別正確率的影響比較大。表7為實驗數據放在3種不同的網絡模型中得到的識別精度，顯然，改進的LeNet-5網絡比其它兩種網絡模型對實驗數據有更好的識別效果。

表4 不同學習率對應識別率結果

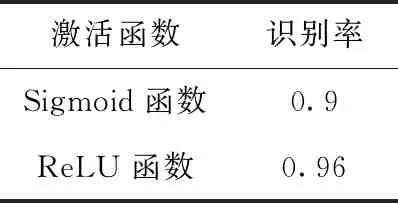
表5 不同激活函數對應識別率結果

表6 有無Dropout對識別率的影響

表7 3種網絡模型結果對比

4 結束語

本文在經典的LeNet-5卷積神經網絡模型的基礎上，將S2層的池化操作設置為均值池化，且S4層的池化操作設置為最大池化，S4層與C5層的連接方式設置為全連接，得到一類新的LeNet-5卷積神經網絡模型，并將其應用于花卉種類識別。實驗結果表明，改進的LeNet-5卷積神經網絡模型可以達到提高花卉分類識別率的目的。但同時存在如下需要進一步改進的問題：

(1)本文對圖像做了灰度化處理，沒有考慮顏色對識別精度的影響，顏色對于測試結果有何影響還尚未給出討論；

(2)是否還有更好的改進方法或者模型，適合研究花卉種類識別的工作，使得識別效果更好，在下一步的工作中將繼續研究。