高樁碼頭樁基沉降研究
周子樂,何明偉
(中交第一航務工程勘察設計院有限公司,天津 300222)
引 言
樁基沉降會對碼頭的安全性和使用性產生一定影響。由于高樁碼頭結構自重小,碼頭整體沉降量不大,因此在國內高樁碼頭設計中通常不對碼頭沉降進行驗算。但是高樁碼頭一般建在軟弱地基上,且外力作用下的各樁的軸力差異較大,因此各樁會產生一定量的不均勻沉降。高樁碼頭上部結構為超靜定結構,微小的不均勻沉降就會對上部結構內力產生影響[1]。正在進行的印尼某高樁碼頭項目中,業主要求對樁基沉降進行計算。本文結合該項目對高樁碼頭樁基沉降展開研究,通過理論計算和數值模擬兩種方法對高樁碼頭樁基沉降量進行了計算,得出了樁基的均勻沉降和差異沉降量,并通過對比驗證確定合理的樁基沉降計算方法,為以后樁基沉降計算提供經驗借鑒。
1 計算方法
由于國內高樁碼頭設計中通常不考慮樁基沉降,故在《高樁碼頭設計與施工規范》[2]中沒有關于樁基沉降的計算方法。本文采用采用《建筑樁基技術規范》[3]中樁基沉降計算方法進行理論計算,并采用ALGOR有限元分析軟件進行數值模擬,通過對兩種計算方法結果的對比,驗證計算方法的正確性與合理性。
高樁碼頭的基本單元是橫向排架,故為了簡化計算,將高樁碼頭結構簡化成橫向排架對樁基的整體沉降和不均勻沉降進行計算。
1.1 理論計算
《建筑樁基技術規范》[3]中規定,地基中由樁基引起的附加應力根據考慮樁徑影響的明德林解按公式(1)進行計算。地基中附加應力主要由樁端阻力和樁側阻力引起,第j樁地基的附加應力不僅考慮了j樁自身對地基的產生的附加應力,也考慮了j樁以外其他幾根樁對j樁周圍地基產生的附加應力。
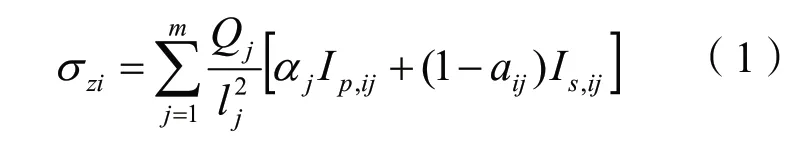
式中:
σzi為水平面影響范圍內各基樁對應力計算點樁端平面以下第i層土1/2厚度處產生的附加豎向應力之和;
m為以沉降計算點為圓心,0.6倍樁長為半徑的水平面影響范圍的基樁數;
Qj為第j樁在荷載效應準永久組合作用下,樁頂的附加荷載(kN);
lj為第j樁樁長(m);
αj為第j樁總樁端阻力與樁頂荷載之比,近似取極限總端阻力與單樁極限承載力之比;
Ip,ij,Is,ij分別為第j樁的樁端阻力和樁側阻力對計算軸線第i計算土層1/2厚度處的應力影響系數,根據樁徑、樁長、樁距和土層深度查表確定。
采用單向壓縮分層總和法計算土層沉降,并計入樁身壓縮se,樁基最終沉降量按下式計算:
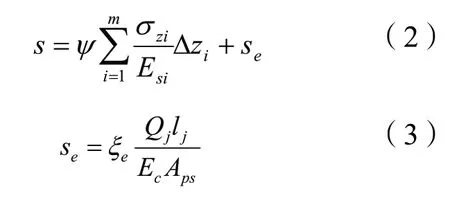
式中:
Ψ為沉降計算經驗系數,無當地經驗時,可取1.0;
Esi為第i計算土層的壓縮模量(MPa);
Δzi為第i計算土層厚度(m);
se為計算樁身壓縮;
ξe為樁身壓縮系數,端承型樁,取ξe=1.0,摩擦型樁,當l/d≤30時,取ξe=2/3,l/d≥50時,取ξe=1/2,介于兩者之間可線性插值;
Ec為樁身材料的彈性模量;
Aps為樁身截面面積。
1.2 數值模擬
在有限元分析軟件ALGOR中建立碼頭橫向排架幾何模型,樁與土之間的相互作用采用與土層參數相關的彈簧來模擬,施加相應的荷載與邊界條件,通過計算可以得出樁的軸力和豎向位移。用有限元數值模擬的方法計算樁基沉降的關鍵是正確選取彈簧參數,國內外學者在這方面已經做了大量的工作,得出了模擬樁側和樁端土的彈簧剛度系數[4-6]。本文根據美國地基設計經典著作《Foundation Analysis and Design》[7]中的推薦理論公式對模型中模擬土作用在樁軸向的彈簧剛度系數進行計算,Lysmer等根據彈性半空間理論得出模擬樁端土作用的彈簧剛度系數見公式(4),Rausche[8]在彈性動力學理論基礎上推導出模擬樁側土作用的彈簧剛度系數見公式(5):

式中:
Kb為樁端土的彈簧系數(kN/m);
Gb為樁端土的剪切模量(MPa);
r0為樁的半徑(m);
ν為土的泊松比;
Ks為樁側土彈簧剛度系數(kN/m2);
Gs為樁側土的剪切模量(MPa)。
2 工程實例
印度尼西亞某散貨碼頭采用高樁梁板式結構,碼頭全長220 m,分為3個結構段,排架間距7.35 m。每個橫向排架由7根直徑1 m的鋼管樁組成,從左至右依次編號為1~7號。樁長為60 m,樁頂高程6.5 m,泥面高程-13.5 m,樁底高程-53.5 m。碼頭斷面如圖1。
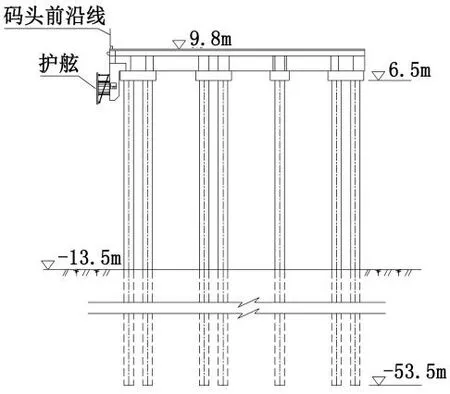
圖1 碼頭斷面示意
根據該項目的地質勘查資料,場地土層分布見表1。
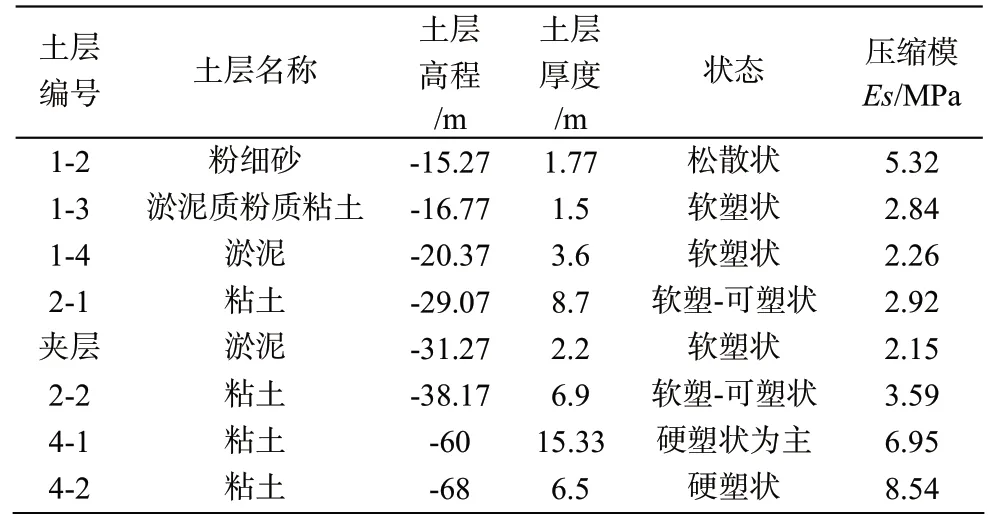
表1 場地土層分布
碼頭承受的主要荷載為自重、門機荷載、系纜力和碼頭面均載,在有限元軟件ALGOR中用m法對排架進行計算,得出準永久組合作用下樁的軸向力見表2。
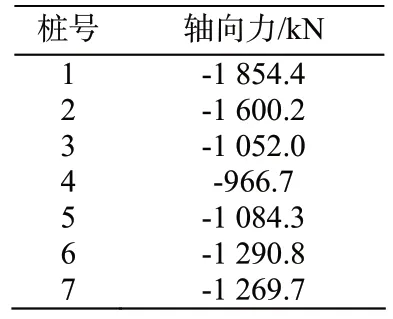
表2 樁基軸向力
3 計算結果
3.1 理論計算
根據《建筑樁基技術規范》(JGJ 94-2008)[3],由樁徑、樁長、計算樁與其他樁之間的距離查表得到α、Ip和Is,取各樁軸向力分別作為相應樁頂附加荷載Q,根據公式(1)計算得到1~7號樁不同土層的附加應力,代入公式(2)可以得到各土層的壓縮量,根據公式(3)計算得到樁自身的壓縮量,土層壓縮量和樁自身壓縮量之和為樁基沉降量,計算結果見表3。
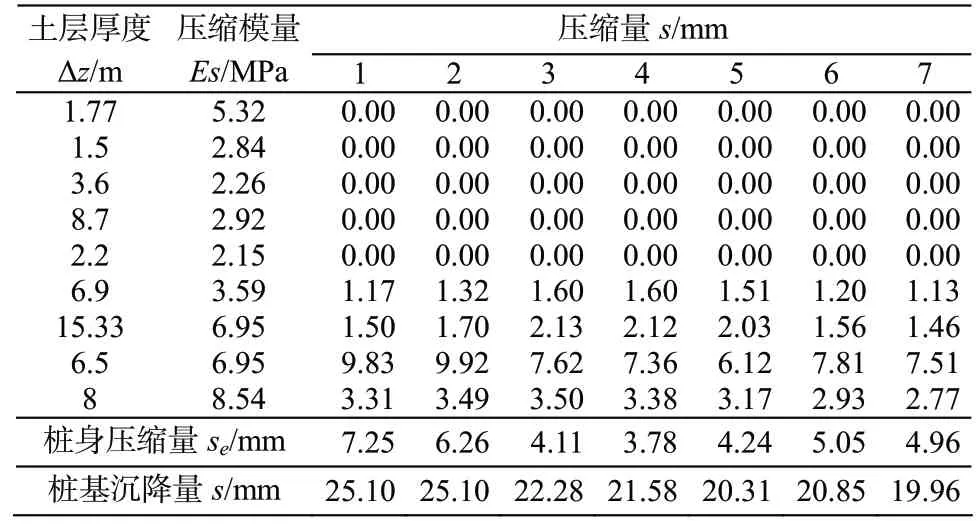
表3 樁基沉降量計算
3.2 數值模擬
在有限元分析軟件ALGOR中,樁與土之間的相互作用可以分為水平方向和豎直方向,分別用水平方向和軸向的彈簧來模擬。水平方向彈簧的彈性系數通過《高樁碼頭設計與施工規范》(JTS 167-1-2010)[2]中的m法來計算。軸向模擬樁端和樁側土作用的彈簧分別用公式(4)和公式(5)來計算,根據土層物理力學指標計算得到樁端和樁側各土層等效豎向彈簧的彈性系數如表4。
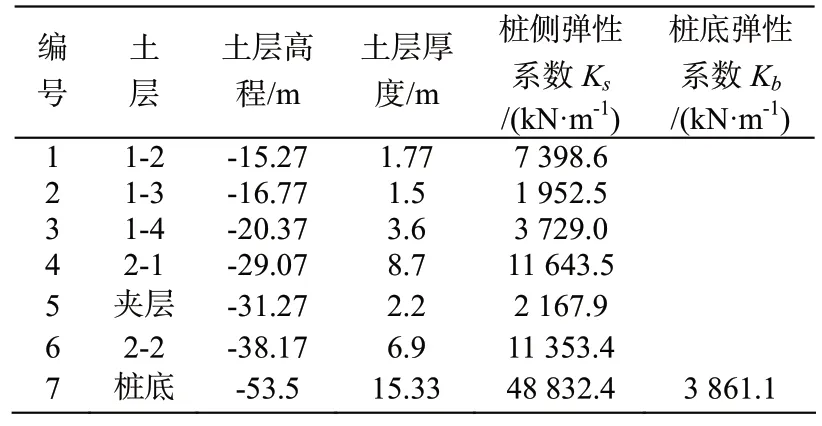
表4 軸向彈簧彈性系數
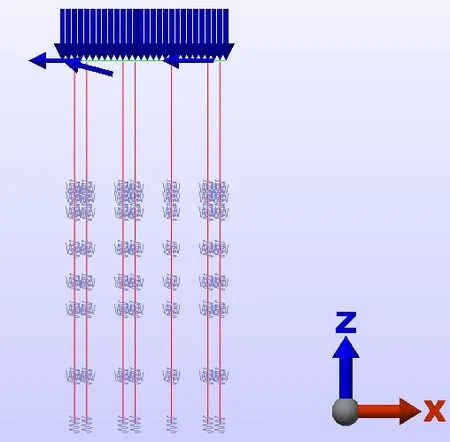
圖2 有限元計算模型
將樁側彈簧作用在樁側各土層的中間位置,樁端彈簧作用在樁底,施加相應的設計荷載,計算模型如圖2。
對模型進行計算,得到正常使用極限狀態準永久組合下的各樁端的豎向位移如表5。
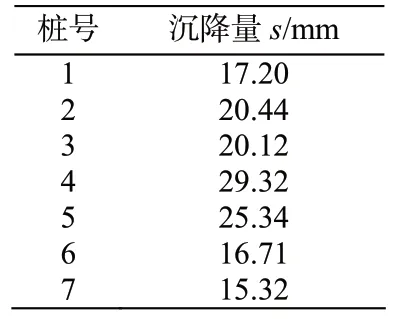
表5 有限元計算樁端沉降
3.3 計算結果對比
對理論計算和有限元數值模擬兩種方法計算得到的沉降量進行對比,結果如圖3。
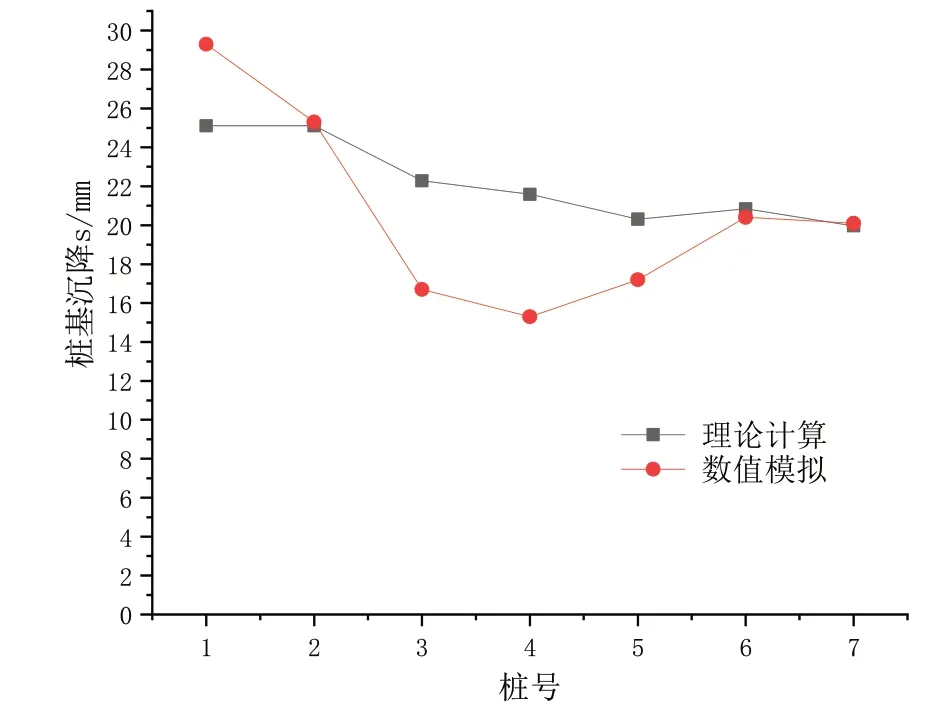
圖3 兩種計算方法結果對比
由圖3可見,兩種方法計算得到的樁基沉降量比較接近,說明計算結果是可靠的。但是理論計算結果比數值模擬結果各樁之間的不均勻沉降更小,究其原因是因為理論計算考慮了另外幾根樁的樁頂荷載對計算樁周圍土體產生的附加應力,所以各樁之間的不均勻沉降更小。而有限元計算只是一根樁在彈簧的約束下的位移,沒有考慮各樁之間的相互影響。所以理論計算更加貼合實際情況。
4 結 語
本文用理論計算和數值模擬兩種方法對高樁碼頭橫向排架的樁基沉降進行了計算,并對兩種計算結果進行了對比分析,可以得出以下結論:
1)高樁碼頭會有幾十毫米級別的整體沉降量,地質條件差或者對沉降要求高的高樁碼頭需要進行樁基整體沉降計算;
2)高樁碼頭橫向排架會有幾毫米的不均勻沉降,橫向排架各樁之間軸力差異較大時需要對各樁之間的不均勻沉降進行計算;
3)理論計算考慮了樁之間的相互作用,計算結果更貼近實際情況,因此《建筑樁基技術規范》(JGJ 94-2008)[3]中單向壓縮分層總和法可以作為一種樁基沉降計算的有效手段。

