衛星定位軌跡最小二乘擬合適應性分析

陳志強，鮑鵬宇，寧云轉

(北京全路通信信號研究設計院集團有限公司，北京 100070)

北斗衛星導航系統是中國自行研制的全球衛星導航系統，可實現與其他國家的衛星定位系統兼容共用，為用戶進行全天候、全天時的定位服務。隨著北斗三號基本系統的建設完成，北斗系統的服務范圍從區域擴展到了全球。近年來衛星定位系統快速發展，世界各國先后開展了基于衛星定位技術的列控系統研發工作，美國通用電氣研發的增強型列車控制系統（Incremental Train Control System，ITCS）已經在我國青藏鐵路穩定運營十余年[1-5]。軌道的地理坐標信息是基于衛星定位列控系統的基礎數據，目前常用的獲取軌道位置的方法包括人工定點采集和曲線擬合兩種方法[6-7]。由于定點采集具有效率低下和容易出現采集錯誤的問題，因此本文對基于最小二乘方法的軌道衛星定位軌跡擬合方法展開研究和討論。

1 最小二乘軌道擬合方法

如圖1 所示，裝有衛星接收裝置的列車從A 點運行到B 點，途中實時接收列車的衛星信息。經過多次往返，采集到軌道的定位數據，通過最小二乘擬合的方式實現軌道定位信息的采集，此方法具有方便快捷，實施簡單的特點。

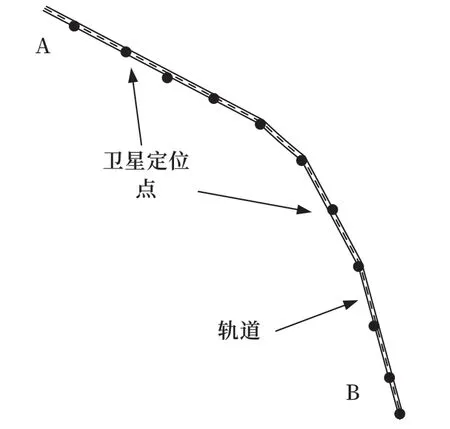
圖1 衛星定位軌跡擬合示意圖Fig.1 Schematic diagram of satellite positioning trajectory fitting

2 最小二乘擬合算法

最小二乘擬合是一種數學優化技術。它通過最小化誤差的平方和尋找數據的最佳函數匹配。利用最小二乘法可以簡便地求得未知的數據，并使得這些求得的數據與實際數據之間誤差的平方和為最小[8]。

待擬合點為 (xi,yi)，其中。欲對這些點進行最小二乘擬合，可以建立方程如公式（1）所示[9]。

顯然，該方程組一般而言沒有解，為獲取最優解，引入最小二乘問題的矩陣形式：

最小化f(a) ：

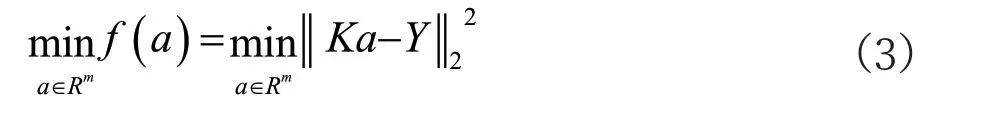
可得到最小二乘問題的最優解：

由于列車軌道具有轉彎半徑大，大多數軌道平直的特點，可對公式（1）進行簡化，令公式（1）的參數m 為2，獲得待擬合點的線性擬合數據。

3 經緯度最小二乘擬合問題分析

經緯度坐標是基于地理坐標系描述的衛星定位原始數據。基于此描述的各點處于球面上，其進行最小二乘擬合時存在2 個問題。

1)球面兩點之間的距離不能使用經緯度差的2范數直接進行描述。公式（2）～（4）所描述的最小二乘方法的優化結果并非最優解。

2)經緯度坐標與平面坐標系是非線性映射的，地理坐標系的線性最小二乘的直線映射到平面坐標系后會變為曲線。

針對上面兩個問題，需要對最小二乘擬合在地理坐標系中使用的適應性進行分析。

3.1 經緯度坐標距離分析

如圖2 所示，A、B、C、D 為地球表面上的點，線段AD 和BC 上所有的點分別有相同的經度，線段AC 和BD 上的點分別有相同的緯度。A、B 兩點的經緯度坐標分別為(a1, β1)和 (a2, β2)。

圖2 經緯度坐標與平面直角坐標映射圖Fig.2 Map of latitude and longitude coordinates and plane rectangular coordinates

為分析最小二乘的適應性問題，不失一般性，可簡化坐標系映射關系。設地理坐標系原點為東經0 度，北緯0 度，則存在某點的坐標為 (a, β)（單位：度），則該點映射到平面坐標系的坐標為(x, y)，其映射關系為：

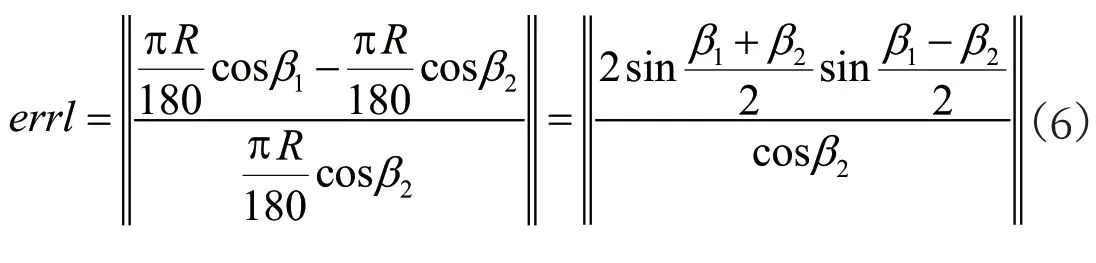
假設1：A、B 兩點距離很近，公式（6）可化簡為：

根據公式（7）可知，線性誤差受到兩個因素的影響：

2)兩坐標點緯度的正切值tanβ2。

根據上述兩個因素可知，若控制errl 小于e，則需要滿足假設2。

引理1：兩坐標點2 范數距離誤差小于其中一個坐標變量之差的誤差。

證明：

設兩坐標點為(x1, y1)和 (x2, y2)，其2 范數距離為，其中a=x1-x2，b=y1-y2。

根據誤差傳遞公式， a 的誤差對l 影響為

因此，有Δl≤ Δa。

同理，有 Δl≤ Δb。

證畢。

綜上，根據引理1，在滿足假設1 和假設2的情況下，可確保兩坐標點的距離誤差小于e，從而最小二乘的解為其在誤差e 控制范圍內的近似最優解。

3.2 經緯度坐標擬合線性分析

待擬合衛星定位點為(αi, βi)，其中。應用公式（1），并取公式（1）的m 為2，對待擬合點進行最小二乘擬合，可以建立方程如公式（12）所示。

其最小二乘最優解為：

為分析地理坐標系與平面坐標系的線性對應關系，需將使用公式（5）代入到公式（1）的參數K和Y 中。

將公式（5）代入最小二乘方法公式（1）的系數K 中，并取公式（1）的m 為2，可得到：

對公式（11）進行簡化，有：

將公式（5）代入最小二乘方法公式（1）的Y中，可得到：

對公式（13）進行簡化，有：

將公式（12）和（14）代入到最小二乘最優解公式（4）中，得到經緯度坐標點對應平面坐標系下的最小二乘最優解：

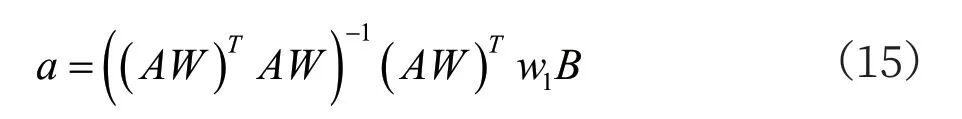
經化簡可得到：

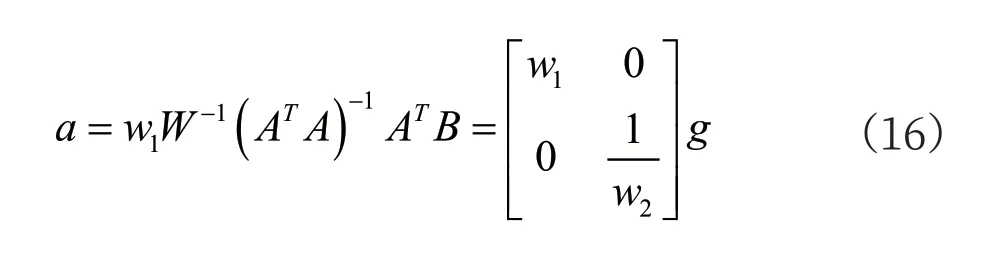
其中，a 和g 分別為平面坐標系和地理坐標系的最小二乘線性擬合最優解。

由此可見，地理坐標系的最優解g=[g0, g1]和平面坐標系的最優解a=[a0, a1]存在一一對應關系。

假設3：假設待擬合點距離很近，其最大與最小經度的余弦值之差小于errβ。

在滿足假設3 的情況下，系數w1和w2均為恒定值，待擬合衛星定位點的最小二乘線性擬合結果 β=g0+g1α 與其在平面坐標系上的映射均為直線，且可經過旋轉和平移得到。

4 結論

本文針對人工采集軌道衛星定位數據存在的問題，提出一種軌道數據最小二乘擬合方法。并針對地理坐標系和平面坐標系的特點，對最小二乘的應用條件進行了分析，提出3 個假設。在滿足3 個假設的情況下，可直接使用最小二乘方法對經緯度坐標進行線性擬合，擬合結果與其在平面坐標系上的映射具有一一對應的線性關系。使用該擬合結果可得到軌道地理信息的近似最優解。本文提出的最小二乘擬合方法可實現軌道的實時運算，提高了擬合效率和軌道數據的可靠性，為軌道信息的采集提供了一種切實可行的方法和理論依據。