電子裝備測試性融合評估方法

尹園威，馬俊濤，姚智剛，解 輝,史 林，呂 萌

(陸軍工程大學石家莊校區 電子與光學工程系，石家莊 050003)

0 引言

測試性是裝備通用質量特性之一，在GJB 2547A-2012中的定義為：“產品能及時、準確地確定其狀態(可工作、不可工作或性能下降程度)，并隔離其內部故障的一種設計特性”[1]。測試性作為裝備的通用質量特性之一，在大型復雜裝備的全壽命周期過程中起了重要作用[2-4]。測試性參數主要包括故障檢測率(FDR)、故障隔離率(FIR)、故障虛警率(FAR)等。

測試性評估，是指采用相應的理論與方法來評價裝備測試性參數達到什么樣水平的過程。如：裝備設計特性的測試性定量評價、測試性建模分析與評估、研制階段的仿真試驗評估與樣機試驗評估、定型階段裝備實物試驗的測試性評估和綜合分析評價等，均是測試性試驗與評估的內容。測試性評估的目的主要有3個：1)對本階段裝備的測試性水平進行評估，為是否轉入下一階段提供依據；2)是測試性驗證試驗，為裝備定型提供依據；3)裝備使用后的測試性信息收集與評價，為研發新型裝備和性能改進提供參考。

實裝測試性試驗存在幾個問題：1)在研和新列裝的電子裝備數量少，使用大數定律的統計方法進行測試性試驗，缺乏足夠的時間和樣本量，而且裝備高可靠性的設計使得自然發生的故障數量少；2)新型復雜裝備集成度高、結構復雜，測試難度大，費用高；3)實物故障注入會對裝備造成損壞，影響裝備的列裝使用，風險大。隨著建模仿真技術的發展，裝備測試性仿真試驗成為測試性評估工作的重要發展方向，具有實裝試驗所不具備的優點：1)降低了可訪問性的限制，可將故障注入到任何位置；2)較少依賴輔助設備及系統接口，也避免了硬件的損壞；3)易改動、可重復、費用低，可獲取大量試驗數據。

因此，用于測試性評估的裝備實裝試驗數據屬于“小子樣”數據，需要綜合使用其他信息來彌補小子樣實物試驗數據的不足，本文采用貝葉斯數據融合的方法融合仿真數據與實裝試驗數據，以提高測試性評估的客觀性與可信度。

1 測試性仿真數據獲取

測試性仿真數據的獲取主要依靠裝備的仿真試驗，是用于獲取測試性仿真試驗數據的主要途徑，主要包含兩項技術：1)裝備仿真模型與故障模型的建立；2)故障模型的建立；3)故障模式選擇與仿真故障注入。

1.1 裝備仿真模型

對于大型復雜電子裝備仿真模型的建立，可采用模塊化、層次化的思想，使用宏建模技術，對某個分系統或部組件進行建模,將其分解為若干塊子電路，之后再組合完成系統的仿真模型。

模塊化設計的實現步驟是：將裝備整體電路依其結構與功能分割成合適的子電路，對各子電路進行分別繪制，完成所有子電路的建模，最后通過連接屬性將它們組合起來，形成整體電路。各子電路都需要經過完整的設計，因此每個子電路用“塊”表示，可在不同的地方重復使用，這就是模塊化的含義。

層次化結構是將電路在垂直方向進行“分割”，每個模塊可以由幾個內部模塊所組成，一直“分割”到最底層模塊，形成層次化結構。在仿真軟件中，是通過層間的輸入/輸出端口、層次方塊和層次管腳實現邏輯上的互聯互通。

1.2 裝備故障模型

通過裝備可靠性資料、設計資料、專家經驗等信息分析裝備的故障模式和故障位置等，并在仿真環境下建立故障模型[5-6]。建立故障仿真模型需要解決以下這幾個問題：

1)元器件級的故障建模。仿真模型應該能夠準確地表達各元器件故障模式的功能行為，達到表現該故障模式的效果，實現途徑有重組法和替換法。

2)故障宏模型。可以把系統中較為復雜的故障模式使用等效替代的方法將其簡化，只考慮輸入/輸出特性的近似建模方法，降低了故障建模的復雜度。對于大型復雜電路或者無法了解其內部結構的電路，需要使用故障宏模型的方法解決“黑匣”問題。

3)層次故障的建模。測試性試驗需要確定裝備的故障層次，依據裝備物理特性與故障特性，采用由下而上的故障建模策略，從底層元器件故障向上到分系統故障來建立層次故障[7-8]。

1.3 仿真故障注入

通過試驗方案確定注入的故障模式、數量、故障位置等，使用故障模型代替原有的正常模型，施加相應激勵即可完成故障的注入。故障仿真注入方法的顯著優點是：可以盡早建立裝備電路的故障仿真模型并進行故障注入，降低了試驗成本，并且加快了測試性工作的進程。

在相應的測試資源條件下對故障進行檢測/隔離，并與故障注入信息進行對比分析，經過統計得到FDR/FIR等測試性參數，獲取裝備測試性仿真試驗數據。

2 測試性數據融合評估方法

測試性數據融合是一種關于測試性數據處理的研究，綜合利用多種數據，對裝備測試性進行全面多維的分析，其實質是利用數學方法的技術手段將不同來源的數據進行綜合，得到更全面客觀的結論。本文中測試性數據主要包括兩部分：測試性仿真試驗數據和測試性實裝試驗數據，因此主要研究這兩類試驗數據的融合處理方法。

2.1 貝葉斯數據融合

由于裝備實裝試驗數據較少導致裝備故障信息的缺失，可以看作是“小子樣”數據，因此我們考慮采用貝葉斯理論將測試性仿真試驗信息作為驗前信息使用起來，以指導現場試驗或者作為現場試驗的補充。

把未知參數θ看成隨機變量，則驗后分布為給定樣本之后的條件分布密度這種方法是與樣本相關的，可以充分地利用驗前信息，解決小子樣試驗情況下的統計分析問題。

貝葉斯數據融合公式為：

(1)

其中:θ代表需要進行評價的參數；x為樣本觀測值；f(θ|x)為樣本的密度函數；π(θ)為驗前分布密度函數；Θ為θ的取值范圍。

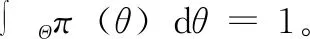
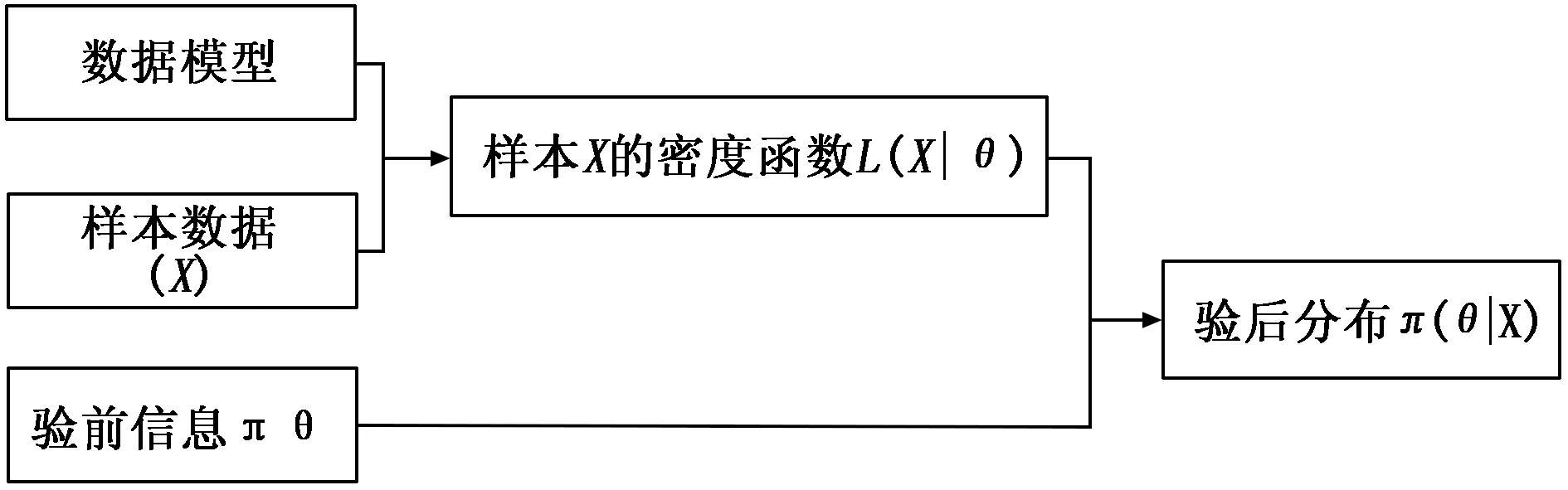
圖1 Bayes數據融合原理

2.2 驗前分布的確定

測試性驗前信息是利用 Bayes 分析方法進行測試性評估和驗證的基礎，大量可信的驗前信息是進行測試性有效評估的前提。測試性驗前信息的來源多種多樣，主要有這幾類[12]：1)測試性設計分析專家在裝備研制過程中，得到的大量測試性經驗知識；2)在設計研制階段，歷次子系統/部組件試驗得到的測試性信息；3)通過建立裝備虛擬樣機、仿真模型等技術進行故障注入，得到的測試性試驗數據；4)裝備新型號的研制，一般與原型號有著一定的技術繼承，因此可以間接利用原有的測試性信息。

如果使用仿真試驗數據作為驗前信息進行數據融合，需要確定使用的驗前信息與現場試驗信息服從同一分布，兩者是相容的、一致的，試驗產品具有技術狀態的一致性。之后使用驗前信息來確定參數的驗前分布，再利用試驗數據確定參數的驗后分布。

對于試驗數據驗前分布的確定，通常有這幾種方法：1)Bootstrap 方法；2)隨機加權法；3)最大熵法；4)經驗Bayes方法；5)共軛分布法。工程上經常用共軛分布法進行運算。

共軛分布的定義為：設θ是總體分布中的參數，π(θ)是θ的驗前分布，如果后驗分布π(θ|x)與驗前分布π(θ)具有相同的函數形式，則稱π(θ)是θ的共軛驗前分布，即驗前、驗后的分布具有相同的形式。

在FDR/FIR的測試性評估試驗中，結果只有兩種情況：檢測成功和檢測失敗。其總體分布為二項分布，采用的共軛分布為貝塔分布，貝塔分布是解決FDR/FIR驗證評價的關鍵，其主要性質包括：貝塔分布曲線與分布參數的關系、先驗分布的期望與方差、后驗分布一階矩(期望)與二階矩。

對于成敗型數據X=(n,f)，FDR/FIR的估計值q可認為是成功次數s(s=n-f)出現的概率，其數學模型為：

(2)

對于貝塔分布，其密度函數為：

(3)

作為先驗分布，貝塔分布的期望E[q]和方差D[q]的表達式：

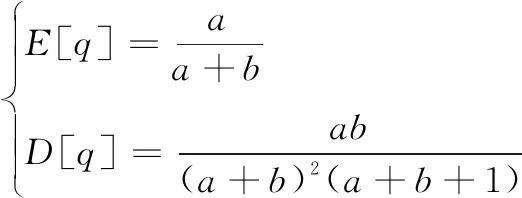
(4)

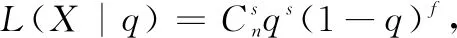
(5)

在平方損失下，FDR/FIR的Bayes估計為其后驗期望值(一階驗后矩)：

(6)

經推導計算可得：

(7)

2.3 驗前信息的處理

當獲得了大量仿真的先驗信息之后，需要對其進行處理，一般是對驗前分布或者驗前參數進行綜合，得到可以使用的驗前信息。這里給出兩種先驗信息的處理方法：等效法與擬合法，具體如下：

假設使用測試性仿真試驗得到m批次的試驗數據，記作：(n1,s1)，(n2,s2)，…，(nm,sm)，其中ni(i=1,2,…,m)是第i次試驗中的故障總數，si(i=1,2,…,m)是第i次試驗中的可以檢測到的故障數，與貝塔分布中參數的關系是ai=si，bi=fi，fi=ni-si。

2.3.1 等效法

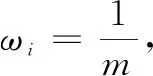
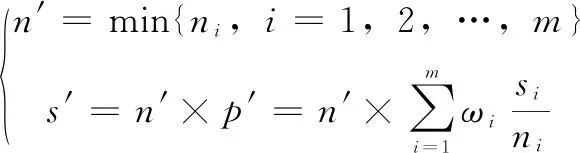
(8)

其中:n′為驗前信息等效的總試驗次數，s′為等效的試驗成功次數。那么驗前分布的超參數a、b分別為：a=s′和b=n′-s′。

2.3.2 擬合法

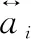
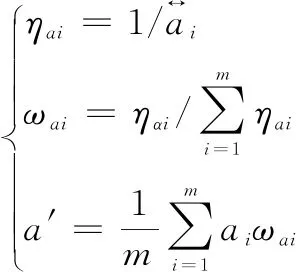
(9)

使用兩種方法得到先驗分布的參數估計值之后，使用貝葉斯融合的方法與實物試驗數據相融合，可得到驗后分布參數，即可得到測試性融合評估的結果。

表1 仿真試驗數據的處理

表2 貝葉斯方法的數據融合評估結果

3 實例分析

對某型裝備建立仿真模型之后進行測試性仿真驗證試驗，以FDR參數為例進行分析，得到五組(n,f)數據，分別為：(63,2)、(61,2)、(58,1)、(68,3)、(58,2)，在裝備實物上展開測試性試驗，得到一組數據為(6,1)。

分別采用上敘的兩種方法進行計算，得到先驗分布超參數。將仿真數據作為先驗信息，使用等效法和擬合法對先驗分布的參數進行估計，得到的驗前信息數據的處理結果如表1所示。使用貝葉斯融合方法對仿真數據和實物數據進行融合，由貝塔分布的性質得到測試性參數的驗后分布參數與點估計值，并運用相應置信度下區間估計的公式得到數據融合評估結果如表2所示。

該裝備測試性設計的目標值為0.9，最低要求值為0.8。在只有現場試驗數據(6,1)的情況下，當置信度為0.9時，查表可得其單側置信下限值為0.4897，這個數據實在太低，令人難以接受。當采用貝葉斯數據融合的測試性評估方法時，融合仿真試驗的測試性先驗信息，使得在相同的實裝試驗數據下，置信下限值達到0.9以上，能夠得出測試性水平合格的結論。同時也可以看出，文中給出的兩種驗前信息處理方法效果基本相同，得到的評估結果相差非常小，均可以應用于測試性評估工作中。

4 結束語

本文基于測試性仿真試驗的貝葉斯數據融合方法，通過獲取測試性仿真試驗數據彌補現場實裝試驗數據量的不足，將仿真試驗數據看作先驗信息，與實裝試驗數據相融合得到測試性評估結果。當融合了先驗信息后，在相同置信度的情況下能夠在對實裝“小子樣”測試性試驗數據進行正確的處理，得到更加合理可信的綜合評估結果。