量子點-Su-Schrieffer-Heeger原子鏈系統的電子輸運特性*

張藍云 薛海斌? 陳彬 陳建賓 邢麗麗

1) (太原理工大學新材料界面科學與工程教育部重點實驗室, 太原 030024)

2) (太原理工大學物理與光電工程學院, 太原 030024)

Su-Schrieffer-Heeger(SSH)原子鏈是典型的具有拓撲邊緣態的一維系統, 并且已在光子和冷原子系統中實驗實現.本文在緊束縛近似下, 利用傳輸矩陣方法研究了量子點-SSH原子鏈系統的電子輸運特性, 這里,量子點的作用是調節SSH原子鏈與電極的隧穿耦合強度.當量子點與SSH原子鏈弱耦合時, 量子點-SSH原子鏈系統的四重簡并邊緣態對應SSH原子鏈存在邊緣態的情形, 而其二重簡并邊緣態對應SSH原子鏈不存在邊緣態的情形; 當量子點與SSH原子鏈強耦合時, 其邊緣態僅在胞內跳躍振幅大于胞間跳躍振幅情形下存在, 此時, SSH原子鏈不存在邊緣態.尤其是, 當量子點-SSH原子鏈系統與外加電極之間為強隧穿耦合時, 其邊緣態的電子共振透射峰的個數將減少2, 例如: 對于四重簡并的邊緣態, 即SSH原子鏈存在邊緣態的情形,其電子共振透射峰的個數將變為2; 而對于二重簡并的邊緣態, 即SSH原子鏈不存在邊緣態的情形, 其電子的共振透射峰將消失.因而, 可以通過調節量子點與SSH原子鏈、外加電極之間的隧穿耦合強度, 觀察邊緣態電子共振透射峰的個數變化情況來判斷SSH原子鏈是否處于非平庸拓撲態.

1 引 言

Su-Schrieffer-Heeger (SSH)原子鏈是具有拓撲特性的最簡單系統[1,2], 且在實驗上已經利用光子[3,4]和冷原子[5]系統實現.尤其是, 在SSH原子鏈系統中, 其受拓撲保護的邊緣態[6]對局部缺陷和系統的無序具有很強的魯棒性, 因而在自旋電子器件和低功耗器件中具有潛在的應用價值[7].因此,如何從理論[8?18]和實驗上[19?22]確定SSH原子鏈拓撲邊緣態的存在成為凝聚態物理中的重要課題之一.其中, 通過研究SSH原子鏈的電子輸運特性對其邊緣態的依賴關系, 從而確定邊緣態存在的電子輸運特性成為一個重要研究課題.例如, SSH原子鏈的電子透射率、電流散粒噪聲和電導表現出新奇的奇偶性[23].在直流偏置電壓下, SSH原子鏈能量分辨地傳輸、電流和散粒噪聲可以用來探測其非平庸拓撲態[24]; 而在交流電場驅動下, 電流的散粒噪聲可以用來測量其拓撲相圖[25].但是, SSH原子鏈與電極之間的隧穿耦合強度對其邊緣態電子輸運特性的影響, 特別是, SSH原子鏈與電極處于強隧穿耦合區域時, 邊緣態與其電子輸運特性的關系, 尚未被揭示.

在本文中, 利用緊束縛近似和傳輸矩陣方法[26]研究了量子點-SSH原子鏈系統的電子輸運性質,并確定其輸運性質與SSH原子鏈邊緣態之間的關系.與SSH原子鏈直接與兩個電極耦合的情形相比, 將SSH原子鏈的左、右端與兩個量子點耦合,可以通過SSH原子鏈與兩個量子點之間的隧穿耦合強度和兩個量子點與外加電極之間的隧穿耦合強度兩個參數, 調節SSH原子鏈與兩個電極的隧穿耦合強度, 為研究SSH原子鏈邊緣態的魯棒性,尤其是, 基于電子輸運特性如何確定SSH原子鏈邊緣態的存在提供一個可選擇的方案.在量子點-SSH原子鏈系統中, 當量子點與SSH原子鏈弱耦合時, 在SSH原子鏈存在邊緣態的情形下, 量子點-SSH原子鏈系統的邊緣態為四重簡并, 而在SSH原子鏈不存在邊緣態的情形下, 其邊緣態為二重簡并.當量子點與SSH原子鏈強耦合時, 量子點-SSH原子鏈系統的邊緣態僅在胞內跳躍振幅大于胞間跳躍振幅情形下存在且為二重簡并, 但是,此時SSH原子鏈不存在邊緣態.研究結果表明, 量子點與SSH原子鏈、兩個電極之間的隧穿耦合強度對其邊緣態電子共振透射峰的個數起決定性作用, 此特性可以用來判斷SSH原子鏈是否處于非平庸拓撲態.

2 物理模型與研究方法

2.1 物理模型

本文考慮的物理模型為量子點-SSH原子鏈系統和兩個外加電極耦合, 如圖1所示, 整個系統的哈密頓量可以表示為

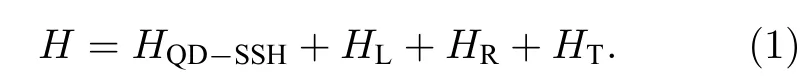
(1)式中右邊第一項為量子點-SSH原子鏈的哈密頓量

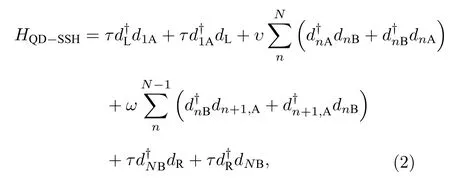
(1)式中右邊第二項和第三項分別表示左電極(源極)和右電極(漏極)的哈密頓量:

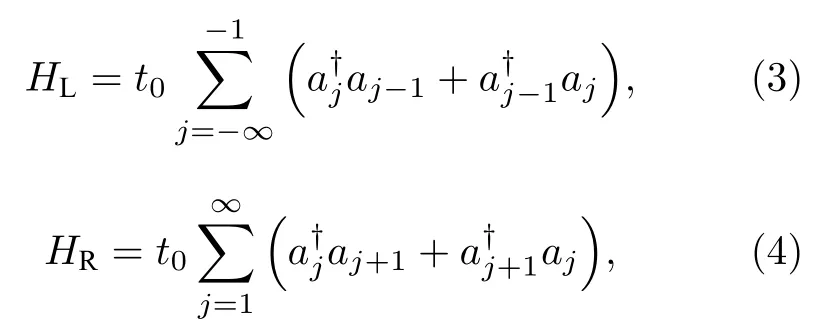
(1)式中第四項表示左右電極與量子點-SSH原子鏈系統之間的隧穿耦合哈密頓量:

其中, tL和 tR分別是左、右導線與量子點-SSH 原子鏈系統之間的隧穿耦合強度.

2.2 研究方法

下面采用傳輸矩陣方法計算電子通過量子點-SSH原子鏈系統的透射率.首先, 將整個系統的波函數 ψ 按照每個“格點”的瓦尼爾態函數展開, 可得:

圖1 量子點-SSH原子鏈系統的示意圖.其中, 空心圓為電極上的原子, 陰影圓表示量子點, 紅色圓表示A原子, 藍色圓表示B原子.t0 是電極上最近鄰兩個原子之間的跳躍振幅, tη(η =L,R) 表示導線與量子點之間的隧穿耦合強度, τ 為量子點與SSH原子鏈之間的隧穿耦合強度, υ 為胞內的跳躍振幅, ω 為胞間的跳躍振幅, N為原胞數目Fig.1.Schematic of the considered quantum dot-SSH chain hybrid system.The hollow circles denote atoms on the leads, the shadow circles are the quantum dots, red circles are the A atoms, the blue circles represent the B atoms.t0 is the hopping amplitude between the two nearest-neighbor atoms on the leads.tη (η =L,R) describes the strength of tunneling coupling between the lead-h and quantum dot-h, τ is the strength of tunneling coupling between quantum dot and SSH chain, υ and ω denote the intra-cell and inter-cell hopping amplitudes, respectively.N is the number of unit cells.

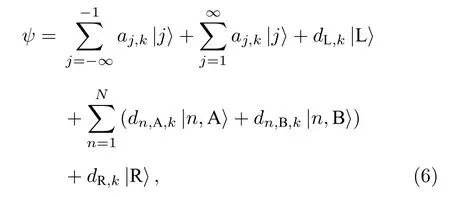
其中: aj,k(j??1) 、 dn,α,k、 aj,k(j?1) 分別是左電極、SSH原子鏈、右電極原子瓦尼爾態函數的幾率幅; dL,k和 dR,k分別是左、右兩個量子點瓦尼爾態函數的幾率幅.這里, k 為入射電子的波矢, 入射電子的能量 E =2t0coska , 其中, 電極上原子的位置能 ε0已選取為0, 電極上最近鄰兩個原子之間的跳躍振幅振幅 t0選取為1, 晶格常數a為1.

為方便計算, 將左、右電極上第j個原子的幾率幅寫成如下平面波的形式:

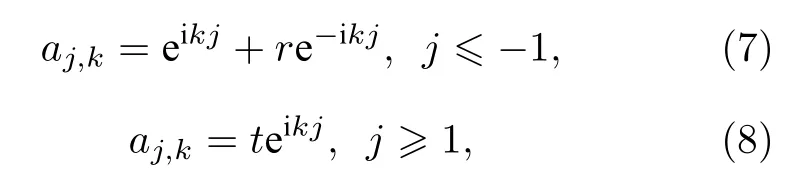
其中, r和t分別是反射和透射的幾率幅.將系統的哈密頓量(1)式和波函數(6)式代入薛定諤方程H|ψ?=E|ψ?, 令方程兩邊相同瓦尼爾態函數的系數相等, 可以得到下面一系列的方程組:

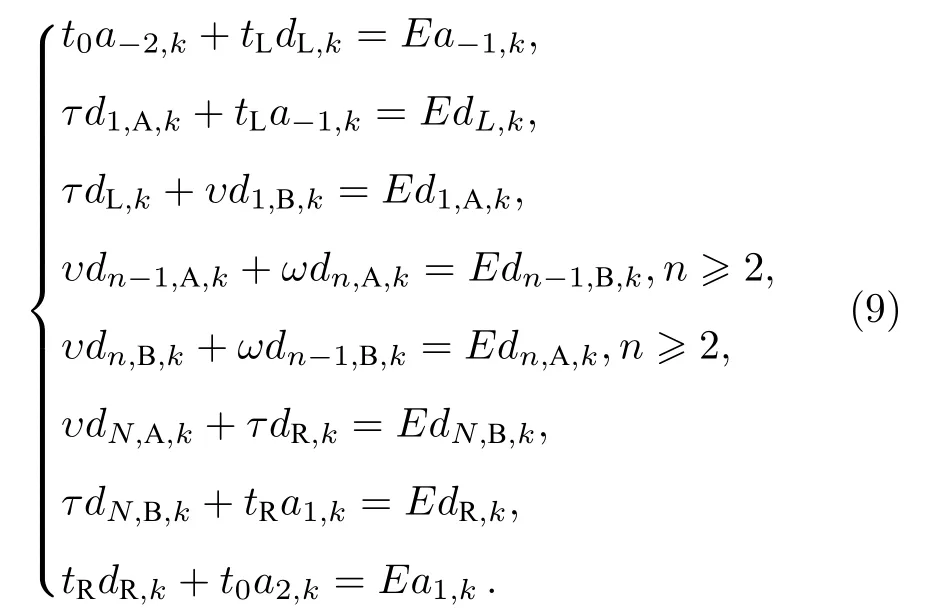
利用傳輸矩陣方法, 可將(9)式寫成如下形式:

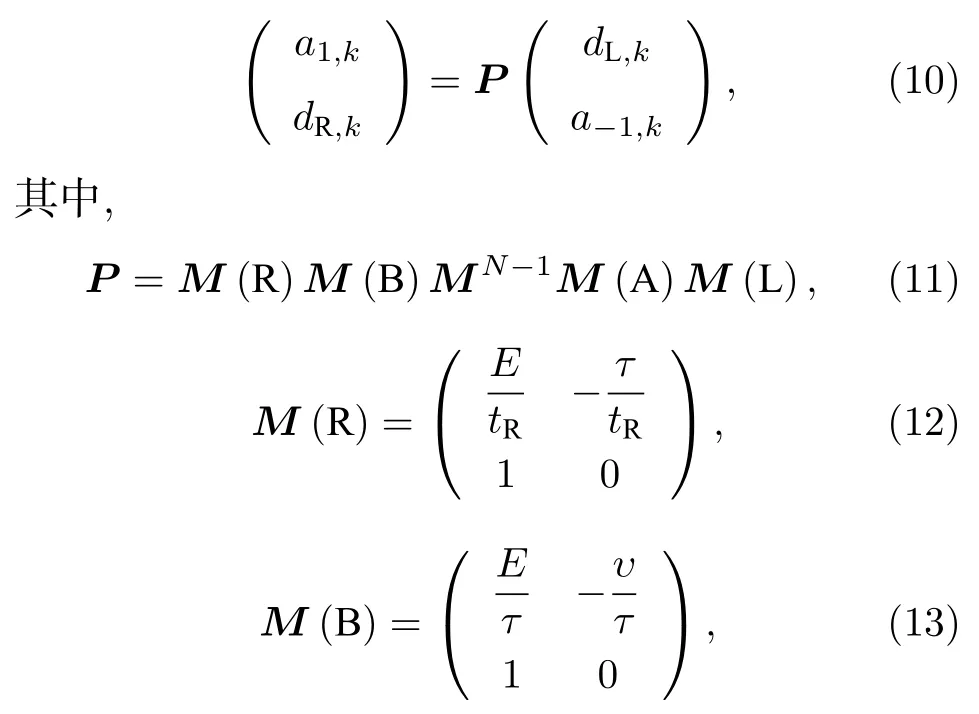
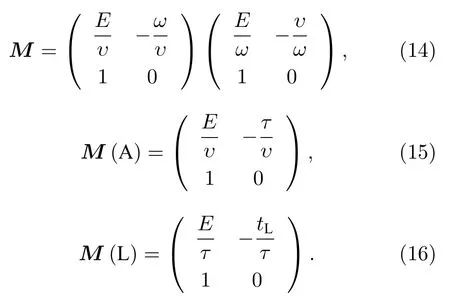
因而, (9)式可進一步簡化為如下形式:

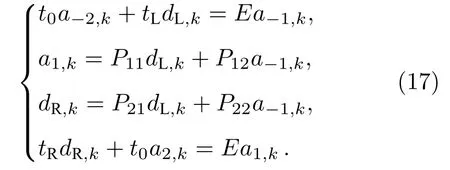
另外, 由(7)式和(8)式可得

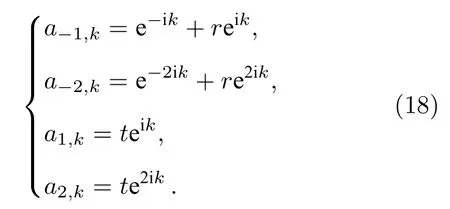
將方程(18)代入方程(17), 可求出量子點-SSH原子鏈系統的透射率

3 數值結果與討論

3.1 量子點-SSH原子鏈系統的能譜圖

對于SSH原子鏈, 其邊緣態在胞內跳躍振幅υ小于胞間跳躍振幅 ω 情形下, 即 υ <ω 情形下存在,如圖2(a)所示.在量子點-SSH原子鏈系統中, 其邊緣態性質依賴于量子點與SSH原子鏈的隧穿耦合強度.當量子點與SSH原子鏈處于弱隧穿耦合區域時, 例如, τ =0.01 , 邊緣態在不同區域具有不同的簡并度, 如圖2(b)所示.當量子點與SSH原子鏈處于強隧穿耦合區域時, 例如, τ =1.00 , 邊緣態僅在 υ >ω 情形下存在, 如圖2(c) 所示.為了確定邊緣態及其簡并度, 圖3給出了SSH原子鏈和量子點-SSH原子鏈系統的邊緣態, 即零能本征值對應的波函數在每個格點位置上的幾率分布, 這里, 零能本征態記為 φμ, 其中 μ 為邊緣態的態指標.

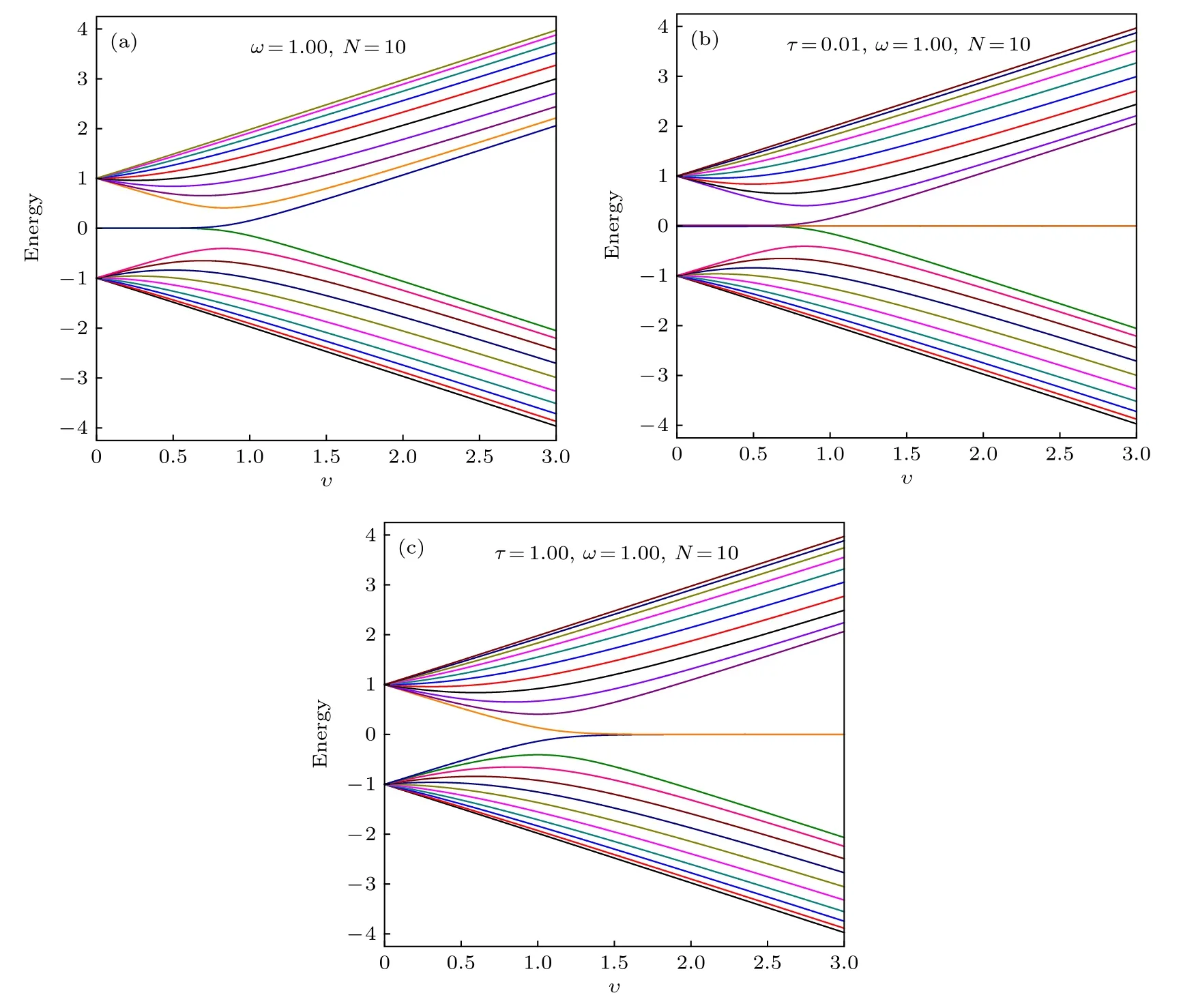
圖2 (a) SSH 原子鏈的能譜圖; (b) 和 (c) 量子點-SSH 原子鏈系統的能譜圖, 其中, (b) τ =0.01 , (c) τ =1.00.胞間跳躍振幅ω=1.00, 原胞數目N=10Fig.2.(a) Energy spectrum of the SSH chain; (b) and (c) Energy spectrum of the quantum dot-SSH chain hybrid system, where(b) τ =0.01 and (c) τ =1.00.Here, ω =1.00 and N =10.

當量子點與SSH原子鏈弱耦合時, 即 τ =0.01 ,在 υ <ω 情形下, 例如, υ =0.50 , 其零能本征態為φ1, φ2, φ3和 φ4, 相應地, 其邊緣態的簡并度為 4.此時, 零能本征態的幾率分布在與SSH原子鏈耦合的兩個量子點上的占據幾率最大, 在SSH原子鏈左、右兩端原子上的占據幾率則次之.因此, 量子點-SSH原子鏈系統的四重簡并邊緣態對應于SSH原子鏈存在邊緣態的情形, 如圖3(a)和圖3(b)所示.在 υ >ω 情形下, 例如, υ =1.50 , 其邊緣態的簡并度為 2, 相應地, 零能本征態為 φ1和 φ2, 雖然其幾率在與SSH原子鏈耦合的兩個量子點上的占據幾率最大, 但是, SSH原子鏈左、右兩端原子的占據幾率并沒有明顯大于其他原子, 因而, 量子點-SSH原子鏈系統的二重簡并邊緣態對應于SSH原子鏈不存在邊緣態的情形, 如圖3(a)和圖3(c)所示.當量子點與 SSH原子鏈強耦合時, 即τ=1.00, 僅在 υ >ω 情形下, 例如, υ =2.00 , 存在二重簡并的邊緣態, 其零能本征態為 φ1和 φ2.此時, 其幾率僅在與SSH原子鏈耦合的兩個量子點上的占據幾率最大, 尤其是, SSH原子鏈左、右兩端原子的占據幾率甚至小于其他原子如圖3(d)所示.因此, 量子點-SSH原子鏈系統二重簡并的邊緣態都對應于SSH原子鏈不存在邊緣態的情形.

3.2 量子點-SSH原子鏈系統的電子輸運特性

3.2.1 量子點與SSH原子鏈弱耦合的情形

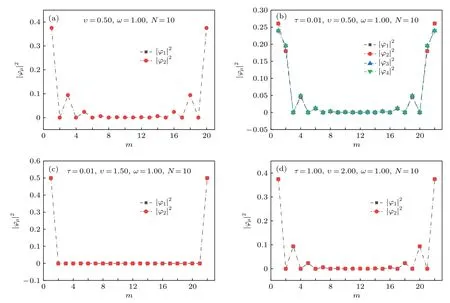
圖3 (a) SSH 原子鏈的零能模波函數在每個格點位置上的幾率分布, 其中, υ =0.50 ; (b)?(d) 量子點-SSH 原子鏈系統的零能模波函數在每個格點位置上的幾率分布, 其中: (b) τ =0.01 , υ =0.50 ; (c) τ =0.01 , υ =1.50 ; (d) τ=1.00υ=2.00Fig.3.(a) The probability distributions of wave functions of the zero-energy modes at each sites in the SSH chain with υ =0.50 ;(b)?(d) The probability distributions of wave functions of the zero-energy modes at each sites in the quantum dot-SSH chain hybrid system, where (b) τ =0.01 , υ =0.50 , (c) τ =0.01 , υ =1.50 , (d) τ =1.00 υ =2.00.

首先, 分析量子點-SSH原子鏈系統四重簡并邊緣態的電子透射率特性, 即圖2(b)中 υ 小于0.8的情形.當量子點-SSH原子鏈系統與外加電極耦合時, 量子點-SSH原子鏈系統與左、右電極的耦合強度 tL和 tR, 將影響量子點-SSH原子鏈系統的電子結構.因而, tL和 tR的數值將影響其電子輸運特性, 尤其是邊緣態的電子輸運特性.為方便討論,這里選取 tL=tR.當量子點-SSH原子鏈系統與電極之間處于弱耦合區域時, 外加電極對量子點-SSH原子鏈系統的電子結構影響很小.對于有限長的SSH原子鏈, 量子點-SSH原子鏈系統的邊緣態, 實際上是由四個能量不相等, 但其數值都接近于零的本征態組成, 如圖4(a)所示.此時, 入射電子將在 Ein=0 附近, 出現四個共振透射峰, 例如,當 υ =0.60 時, 在 tL=tR=0.010 的情形下, 入射電子 能 量 在 Ein=±0.006 和 Ein=±0.010 附近, 出現了四個共振透射峰, 其峰值對應的入射電子能量與圖4(a)的能量本征值定性一致, 如圖5(a)中的實線所示.

但是, 當量子點-SSH原子鏈系統與電極之間處于強耦合區域時, 外加電極將對量子點-SSH原子鏈系統的電子結構產生決定性的影響.相應地,tL和 tR的數值將對入射電子在 Ein=0 附近的電子輸運特性起決定作用.因而, 隨著 tL和 tR的數值逐漸增大, 四個共振透射峰之間谷底的數值將逐漸增大, 如圖5(a)所示, 并逐漸轉變為兩個較寬的透射峰, 如圖5(b)中的虛線和點線所示.之后, 這兩個較寬的透射峰將隨著 tL和 tR數值的繼續增大而形成一個更寬的透射峰, 如圖5(b)中的雙點劃線和5(c)中的實線所示.若繼續增大 tL和 tR的數值, 這個很寬的透射峰將劈裂為兩個透射峰, 最后,在 Ein= ± 0.004 附近形成兩個共振透射峰, 如圖5(c)所示.

為了解釋此現象的物理機制, 在圖4(b)中, 給出了量子點-SSH原子鏈系統與左、右電極第 –1個和第1個原子耦合的系統在零能級附近的能譜圖,這里, 選取 tL=tR=1.000.由圖4(b)可知, 量子點-SSH原子鏈系統與左、右電極第 –1個和第1個原子耦合系統在 υ =0.60 時的能量本征值與這兩個共振透射峰的位置 Ein=±0.004 定性一致.需要說明的是, 量子點-SSH原子鏈系統的零能本征態φ1和 φ2的幾率在SSH原子鏈最左邊和最右邊的兩個原子上占據幾率最大, 如圖6所示.因此, 當量子點-SSH原子鏈系統與電極之間的隧穿耦合強度從弱耦合區域變化到強耦合區域時, 在Ein=0附近, 電子的共振透射峰將從四個減少為兩個.此特性可以用來判斷SSH原子鏈是否處于非平庸拓撲態.

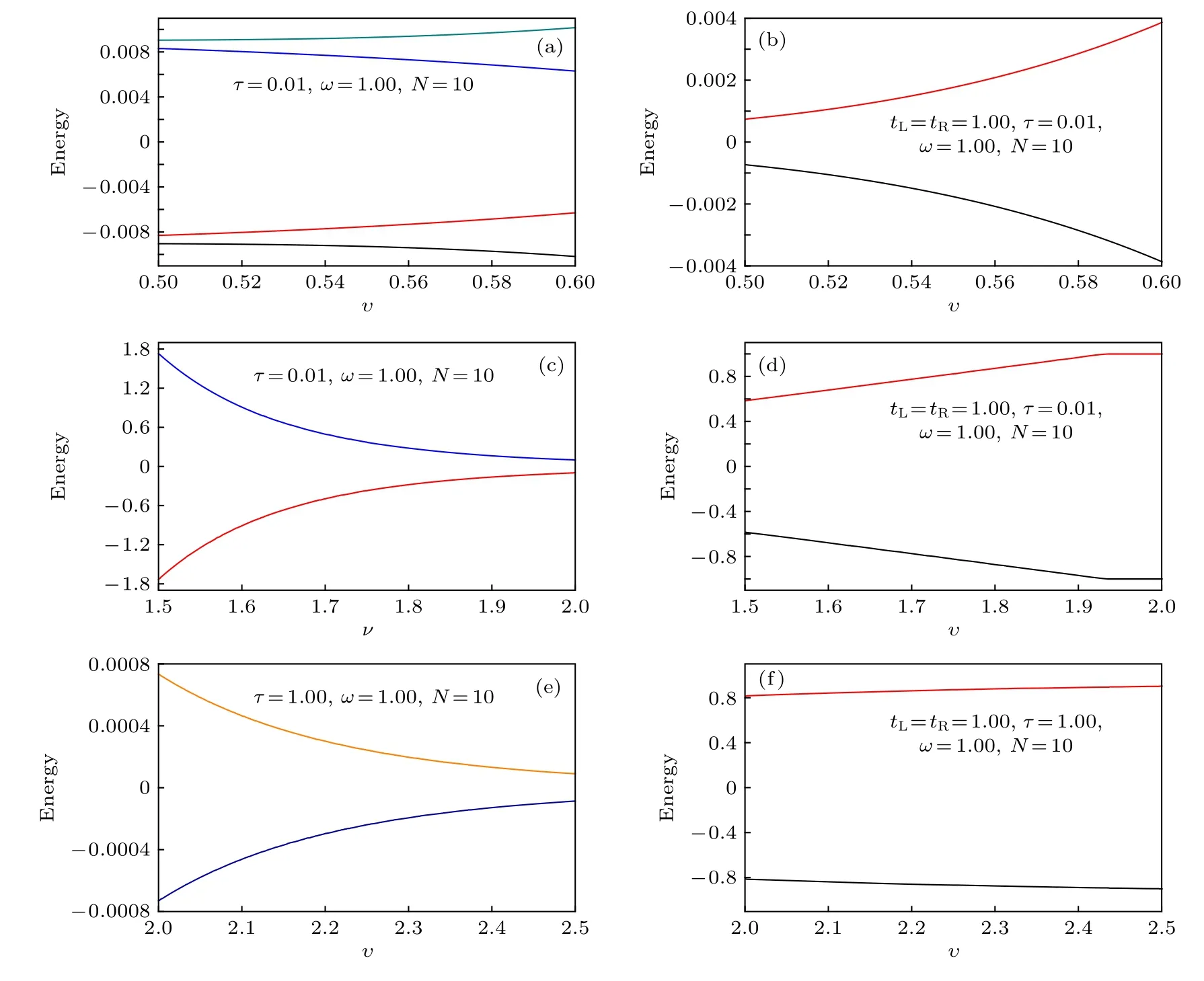
圖4 (a), (c)和 (e)量子點-SSH 原子鏈系統在零能級附近的能譜圖; (b), (d)和 (f)量子點-SSH 原子鏈系統與左、右電極第–1 個和第1個原子耦合的系統在零能級附近的能譜圖, 其中, tL=tR=1.00Fig.4.(a), (c) and (e)Energy spectrum of the quantum dot-SSH chain hybrid system in the vicinity of the zero energy; (b), (d) and(f) Energy spectrum of the quantum dot-SSH chain hybrid system coupled to the first atom (–1) of the left lead and the first atom(1) of the right one in the vicinity of the zero energy at tL=tR=1.00.

其次, 分析量子點-SSH原子鏈系統的二重簡并邊緣態的電子透射率特性, 即圖2(b)中 υ 大于0.8的情形.當量子點-SSH原子鏈系統與電極之間處于弱耦合區域時, 外加電極對量子點-SSH原子鏈系統的電子結構影響很小.對于有限長的SSH原子鏈, 量子點-SSH原子鏈系統的邊緣態,實際上是由兩個能量不相等, 但其數值都接近于零的本征態組成, 如圖4(c) 所示.此時, 入射電子將在 Ein=0 附近, 出現兩個共振透射峰, 例如, 對于υ=1.50的情形, 當 tL=tR=0.0001 時, 入射電子能量在 Ein= ±1.8×10?6附近, 出現了兩個共振透射峰, 其峰值對應的入射電子能量與圖4(c)的能量本征值定性一致, 如圖7(a1)中的實線所示.

但是, 當量子點-SSH原子鏈系統與電極之間處于強耦合區域時, 外加電極將對量子點-SSH原子鏈系統的電子結構產生決定性的影響.相應地,tL和 tR的數值將對入射電子在 Ein=0 附近的電子輸運特性起決定作用.例如, 隨著 tL和 tR數值的增大, 在 Ein= ±1.8×10?6附近的兩個共振透射峰,將逐漸展寬, 并且兩個共振透射峰之間谷底的數值將逐步上升, 如圖7(a1)所示.若繼續增大 tL和tR的數值, 兩個共振透射峰將變成一個較寬的共振峰, 如圖7(a2) 中的虛線和點線所示.當 tL和 tR大于某一數值時, 例如, 當 tL=tR=0.0029 時, 較寬的共振透射峰將消失, 入射電子的透射率將趨于零.此現象同樣可以用量子點-SSH原子鏈系統與左、右電極第? 1 個和第 1 個原子耦合的系統在零能級附近的能譜圖定性解釋, 這里, 選取tL=tR=1.000.由圖4(d)可知, 當量子點-SSH 原子鏈系統與電極之間處于強耦合區域時, 外加電極與量子點-SSH原子鏈系統之間強的隧穿耦合相互作用, 將導致量子點-SSH原子鏈系統的邊緣態消失, 因而, 入射電子在 Ein=0 附近的電子透射率將趨于零.

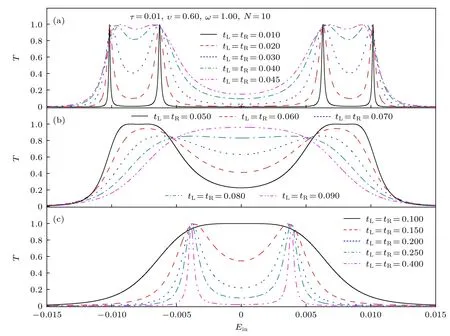
圖5 對于不同的隧穿耦合強度, 量子點-SSH 原子鏈系統的電子透射率隨入射電子能量的變化.其中, τ =0.01 , υ =0.60 ,ω=1.00, N=10Fig.5.The transmission probability versus the energy of incident electron for different strengths of tunneling coupling at τ =0.01 ,υ=0.60, ω =1.00 and N =10.

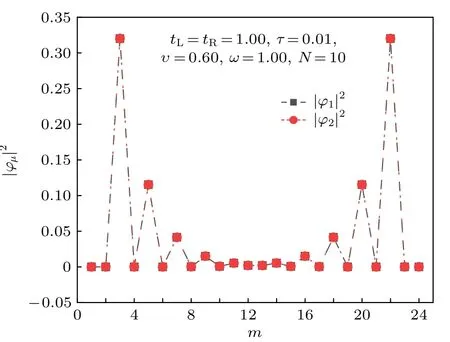
圖6 量子點-SSH 原子鏈系統與左、右電極第–1 個和第1個原子耦合系統的零能模波函數在每個格點位置上的幾率分布.其他參數與圖5相同.Fig.6.The probability distributions of wave functions of the zero-energy modes at each sites in the quantum dot-SSH chain hybrid system coupled to the first atom (–1) of the left lead and the first atom (1) of the right one.The other parameters are the same as in Fig.5.

當胞內跳躍振幅 υ 增大時, 例如, υ =2.00 , 此時, 入射電子在 Ein= ±1.0×10?7附近出現兩個共振透射峰, 如圖7(b1) 所示.與 υ =1.50 的情形相比, 其峰值對應的入射電子能量變小, 但是, 隨著tL和 tR數值的逐漸增大, 其在 Ein=0 附近的電子輸運特性與 υ =1.50 情形相同.這里, 需要說明的是,對于 υ =2.00 的情形, 當 tL和 tR在一個較小的數值時, 例如, tL=tR=0.0007 , 入射電子在兩個共振透射峰位置的透射率就變為零, 如圖7(b2)所示.因此, 可以通過將 tL和 tR的數值從小到大逐漸變化, 然后, 觀察入射電子在 Ein=0 附近共振透射峰的個數變化情況來判斷SSH原子鏈是否處于非平庸拓撲態.

3.2.2 量子點與SSH原子鏈強耦合的情形

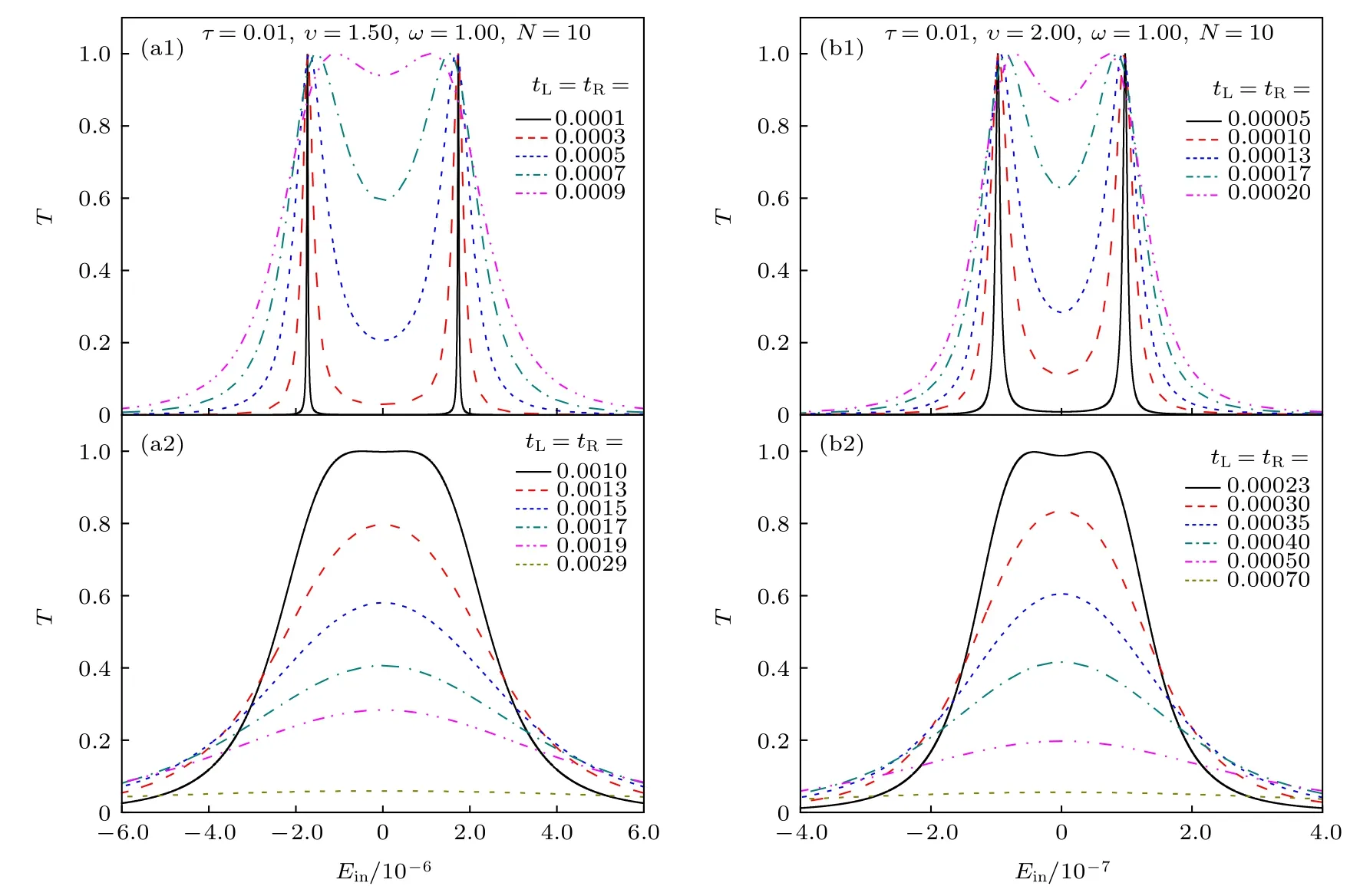
圖7 對于不同的隧穿耦合強度, 量子點-SSH 原子鏈系統的電子透射率隨入射電子能量的變化.其中, τ =0.01 , ω =1.00 ,N=10.(a1)和 (a2) υ =1.50 ; (b1)和 (b2) υ=2.00Fig.7.The transmission probability versus the energy of incident electron for different strengths of tunneling coupling at τ =0.01 ,ω=1.00 and N =10.(a1) and (a2) υ =1.50 ; (b1) and (b2) υ =2.00.

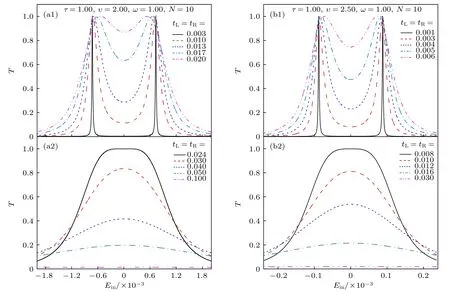
圖8 對于不同的隧穿耦合強度, 量子點-SSH 原子鏈系統的電子透射率隨入射電子能量的變化.其中, τ =1.00 , ω =1.00 ,N=10.(a1)和 (a2) υ =2.00 ; (b1)和 (b2) υ=2.50Fig.8.The transmission probability versus the energy of incident electron for different strengths of tunneling coupling at τ =1.00 ,ω=1.00 and N =10.(a1) and (a2) υ =2.00 ; (b1) and (b2) υ =2.50.

對于量子點與SSH原子鏈之間強耦合的情形,即在 τ =1.00 情形下, 當 υ 大于 1.50 時, 量子點-SSH原子鏈系統具有二重簡并的邊緣態, 如圖3(d)所示.此時, 入射電子在 Ein=0 附近的邊緣態電子輸運特性與量子點-SSH原子鏈弱耦合時二重簡并的邊緣態情形相同, 即, 當量子點-SSH原子鏈系統與電極之間的隧穿耦合強度從弱耦合區域變化到強耦合區域時, 在 Ein=0 附近, 電子的兩個共振透射峰將逐漸消失, 如圖8所示.此特性同樣可以用來判斷SSH原子鏈系統是否處于非平庸拓撲態.但是, 這里共振透射峰對應的電子入射能量相對大一些, 例如, 對于 υ =2.00 的情形, 入射電子能量為Ein=±0.0007, 如圖8(a1) 所示, 其峰值對應的入射電子能量與圖4(e)的能量本征值定性一致, 并且電子共振透射峰的變化過程可以用量子點-SSH原子鏈系統與左、右電極第 –1個和第1個原子耦合系統在零能級附近的能譜圖定性解釋.

當胞內跳躍振幅 υ 增大時, 在 Ein=0 附近, 電子共振透射峰的峰值對應的入射電子能量將變小,例如, 當 υ =2.50 時, 其入射電子在Ein=±0.0001附近出現兩個共振透射峰, 如圖8(b1)所示; 并且當 tL和 tR取一個較小的數值時, 例如, tL=tR=0.030, 入射電子在兩個共振透射峰位置的透射率就變為零, 如圖8(b2)所示.因而, 同樣可以通過調節 tL和 tR的數值, 觀察入射電子在 Ein=0 附近共振透射峰的個數變化情況來判斷SSH原子鏈是否處于非平庸拓撲態.

4 結 論

本文研究了量子點-SSH原子鏈系統的電子輸運特性, 發現量子點-SSH原子鏈系統四重簡并的邊緣態對應于SSH原子鏈存在邊緣態的情形, 而其二重簡并邊緣態對應于SSH原子鏈不存在邊緣態的情形.當量子點-SSH原子鏈系統與外加電極耦合時, 電子在 Ein=0 附近共振透射峰的個數, 將隨著量子點-SSH原子鏈系統與左、右電極耦合強度 tL和 tR的數值從小到大, 減少兩個.例如, 對于四重簡并邊緣態的情形, 其共振透射峰的個數將變兩個, 而對于二重簡并邊緣態的情形, 其共振透射峰將消失.因此, 可以通過將量子點-SSH原子鏈系統與外加電極之間的隧穿耦合強度從弱到強, 觀察電子在 Ein=0 附近共振透射峰的個數變化情況來判斷SSH原子鏈是否處于非平庸拓撲態.