利用非穩態泊松模型對云南地區地震危險性進行概率預測*
錢曉東,彭關靈,賀素歌
(云南省地震局,云南 昆明 650224)
0 引言
在地震發生隨時間變化的統計模型中,穩態泊松過程在中長期地震預測和地震危險性分析中得到廣泛應用(Cornell,1968;Der,Ang,1977;張永慶等,2007;蘇有錦,李忠華,2011)。在穩態的泊松過程中,地震事件的平均發生率λ是一個常數,實際上地震的發生在時間分布上極不均勻,往往表現出間歇-成簇狀發生,具有平靜-活躍特征,λ會出現較大的變化。有的學者提出雙泊松模型(Bender,1984),分別計算地震平靜期和活躍期平均發生率λ來模擬地震發生過程,這種方法仍然未能解決地震發生率λ是一個隨時間而變化的量的事實,因為地震的發生具有自相似性,即使在活躍期或平靜期中,地震的發生仍然具有與整個序列相似的平靜-活躍特征。
為了更加真實地描述區域地震活動,Hong和Guo(1995)提出一種非穩態泊松過程,當地震事件以非穩態泊松過程發生時,事件的發生率是一個隨時間而變化的函數λ(t),他們采用U形函數的發生率來模擬強震或強震群后的地震活動減弱—平靜—增強過程。國內一些學者也采用指數函數的發生率來模擬強震活動過程(傅征祥等,1998;劉杰等,1998;李冬梅,2000;劉英等,2003),由于不同區域強震活動不同,他們使用的指數函數具體形式存在差異,如單指數、雙指數形式等。在目前地震預測預報從經驗向定量化發展的過程中,用定量的方法衡量一個地區地震活動的強弱已越來越引起廣大學者的重視,本文對比穩態與非穩態泊松模型的差異,尋找并建立適合云南地區強震活動的地震發生率函數λ(t),并對云南不同地震帶進行定量化強震概率預測。
1 穩態和非穩態泊松過程
在隨機過程理論中將隨機過程劃分為平穩(穩態)隨機過程和非平穩(非穩態)隨機過程,如果過程的統計特性(均值、方差等)不隨時間的推移而變化,則為平穩隨機過程,平穩過程的所有樣本曲線都會圍繞一條水平直線上下波動,而非平穩隨機過程的統計特性則隨著時間的推移而變化(數學手冊編寫組,1979)。在地震領域中,地震概率預測模型中比較常用的概率密度函數有泊松分布模型、對數正態分布模型、韋伯爾分布模型、布朗流逝時間分布模型、伽瑪分布模型等,其中泊松分布模型在實際工作中應用最廣泛(Kagan,Jackcon,1999;Matthewsetal,2002)。
泊松過程模型分為穩態和非穩態模型。非穩態泊松過程是一個獨立增量假定的計數過程,在時間間隔[t1,t2]內,泊松事件發生的數目是n=N(t2)-N(t1)的概率為(Hong,Guo,1995):
(1)
式中:n=0,1,2,…;v(τ)是瞬時平均發生率;τ是距離最后一次地震的逝去(經歷)時間。當事件以非穩態泊松過程發生時,事件重復發生的時間(復發時間)T也是一個隨機變量,與該隨機變量有關的概率,可由累積分布函數描述,非穩態泊松過程復發時間T的累積分布函數為(Hong,Guo,1995):
(2)
當瞬時平均發生率為常數,即v(τ)=v時,稱為穩態泊松過程,從式(1)可得穩態泊松過程在時間t內發生n次地震的概率為:
(3)
從式(2)可得穩態泊松過程累積分布函數為:
FT(t)=1-exp(-vt)
(4)
式(4)也可理解為在時間t內至少發生一次地震的概率。對于穩態泊松過程恒定平均發生率vc,可由下式求出:
(5)
式中:T為研究時間段的長度;N為在T內的地震總數。
2 穩態和非穩態的平均發生率
2.1 模型選擇
許多學者利用不同模型對強震的平均發生率進行了有益的研究和探索,研究主要集中在強震的累積地震次數隨時間變化模型的探討上,張國民和傅征祥(1985)通過對華北強震時間分布特征研究,認為大地震的累積頻度曲線隨時間的變化呈指數函數形式;秦嘉政等(2009)對云南強震活動時間間隔研究認為,地震的累積頻次隨發震時間呈冪函數變化;傅征祥等(1998)和劉杰等(1998)利用一個假想的泊松分布時間序列,分別采用雙指數和指數模型對強震發生率進行了研究,本文將采用相同的時間序列系統地對事件累積次數隨時間的變化規律進行研究。
假設地震事件序列相鄰地震間隔時間為:1,3,4,5,10,30,40,50。考慮3種典型排列方式:時間間隔遞減、時間間隔遞增和時間間隔不規則,分別表示地震活動的加速、減速和線性變化。采用Matlab語言非線性回歸模型方法進行參數估計(陳桂明等,2002),對3種排列方式下冪函數、指數函數和雙指數函數模型進行非線性擬合參數計算,結果表明冪函數方法直接擬合效果最佳。圖1作為例子給出冪函數模型非線性擬合曲線,可以看到,累積曲線的變化趨勢與實際累積頻次符合程度較好。
2.2 地震發生率
假設地震事件為泊松過程,地震累積頻度N(t)是一種呈冪指數的增長過程:
N(t)=atb+c
(6)
式中:a,b和c是常數,根據非線性回歸模型方法可對參數進行估計。
對于穩態泊松過程,地震事件的平均發生率vc為常數,由式(5)計算得到vc=0.06次/年。而對于非穩態泊松過程,地震事件的瞬時發生率v(t)為:
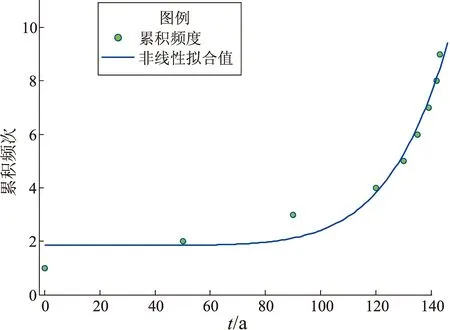
(a)時間間隔Δt遞減
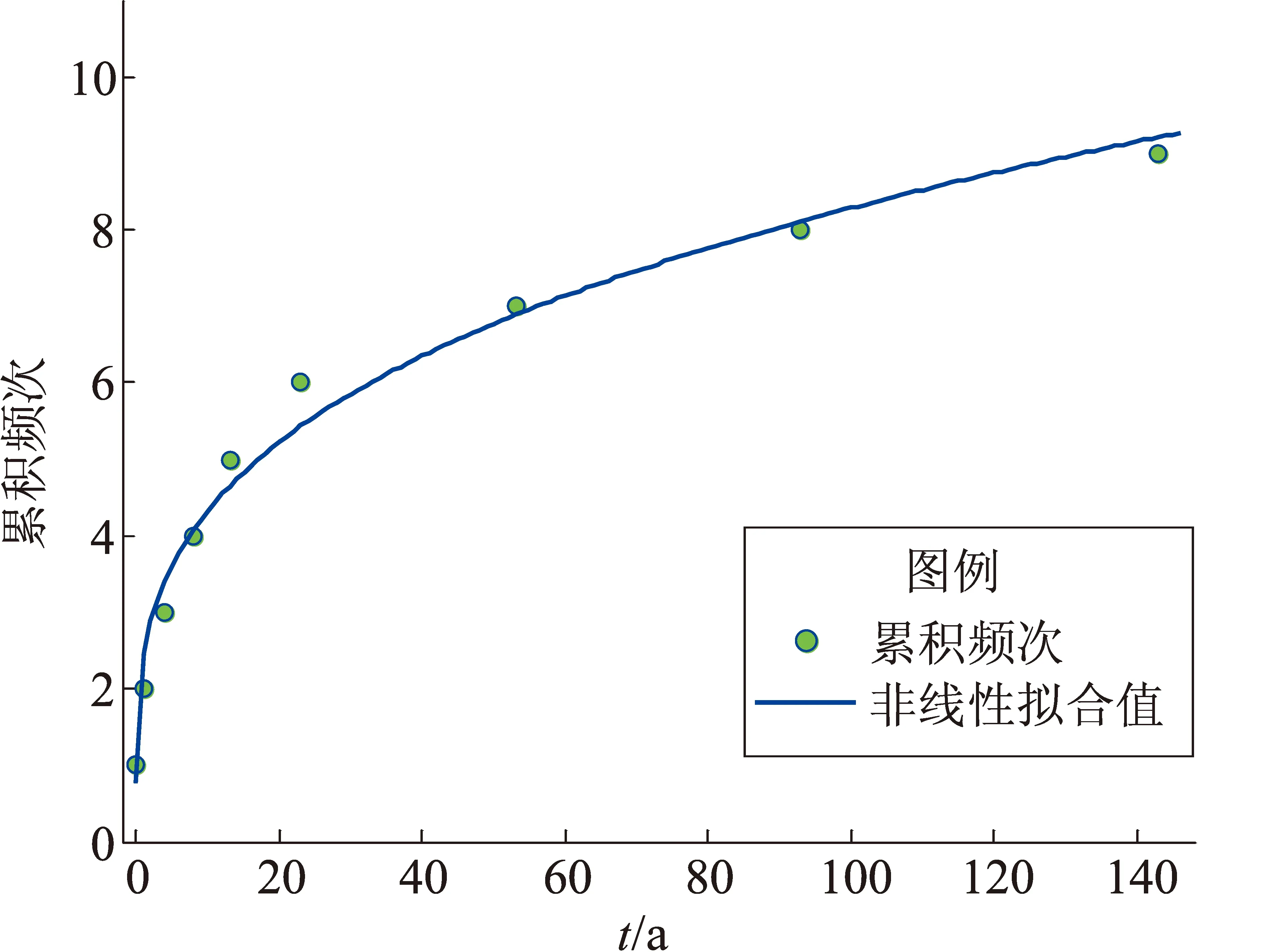
(b)時間間隔Δt遞增
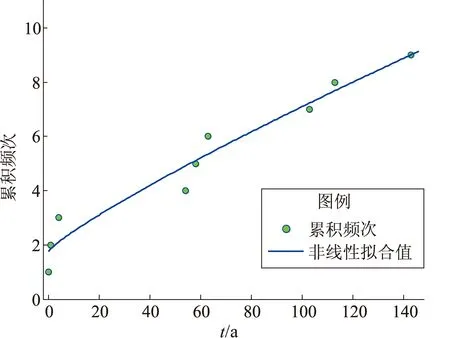
(c)時間間隔Δt不規則
(7)
式中:v(t)為包含a,b 2個參數的t時刻的瞬時發生率。圖2作為例子給出假想地震事件時間間隔逐漸減小情況下累積頻度和發生率。由圖2a可見,對于穩態泊松過程,累積頻度N隨時間t呈線性增長,發生率vc為直線的斜率。對于非穩態泊松過程,累積頻度N隨時間t呈非線性增長,隨著時間的增長單位時間發生的地震越多。圖2b顯示,對于穩態泊松過程,發生率vc為水平直線,在整個過程中恒定不變。對于非穩態泊松過程,根據式(7)計算的各個時刻的瞬時發生率v(t)呈非線性變化。
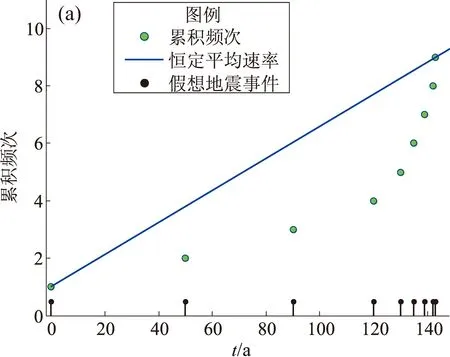
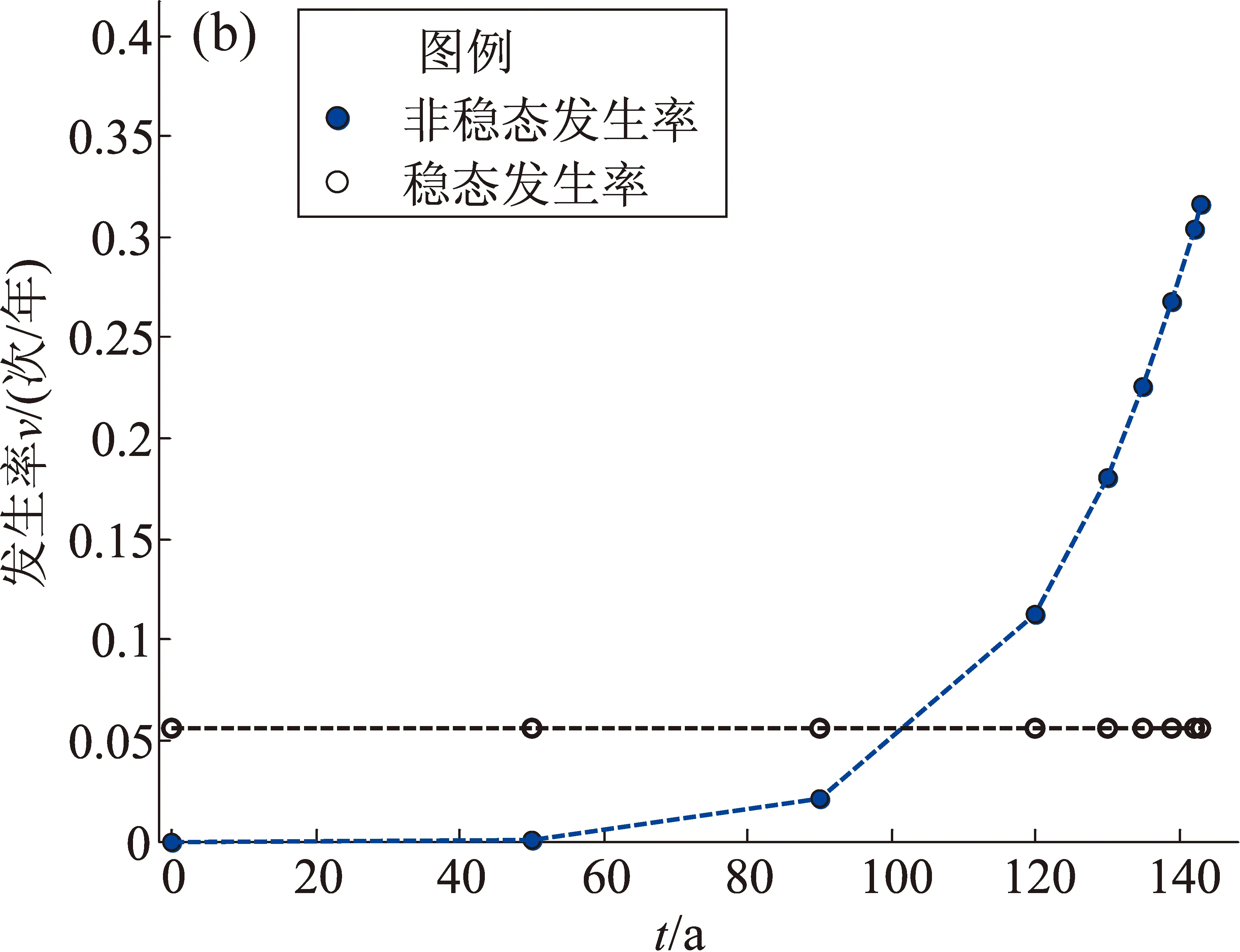
圖2 地震事件時間間隔逐漸減小情況下累積頻次(a)和地震發生率(b)Fig.2 Cumulative frequency and earthquake occurrence rate with decreasing time interval of earthquake events
2.3 地震發生概率
對于穩態泊松過程,根據式(4)和(5)可得(未來)時間t內至少發生一次地震的概率為:
(8)
式中:T為研究時間段的長度;N為在T內的地震總數。
對于非穩態泊松過程,根據式(2)和(7),假定t0時刻發生一次地震,則在[t0,t0+t]時段內至少發生一次地震的概率為:
(9)
圖3給出假想地震序列時間間隔逐漸減小情況下累積頻度擬合預測及概率,在圖3a中,空心圓表示根據非線性擬合曲線給出的當最后一次地震后t=10 a時刻的預測值。在圖3b中,水平虛線表示不論事件發生在什么時間,其后t=10 a的事件發生的概率都是相同的,為P=0.43。在非穩態泊松過程中,地震發生呈非線性加速增加,間隔時間越來越短,越到后面越容易發生地震,如圖3b所示,在最初的時間間隔Δt較長的3個點發震概率P較低,低于水平直線穩態泊松過程,從第四個點開始發震概率P激劇增加。
穩態泊松過程模型表示的是地震序列整體的平均狀態,不考慮序列地震的活躍、平靜過程,得到的發震概率P在整個研究時間段內都是相同的。而在非穩態泊松過程模型中,隨著地震的活躍、平靜狀態不同,模型得到的發震概率P也不相同,更能真實地反映不同時間段發生地震的危險程度。
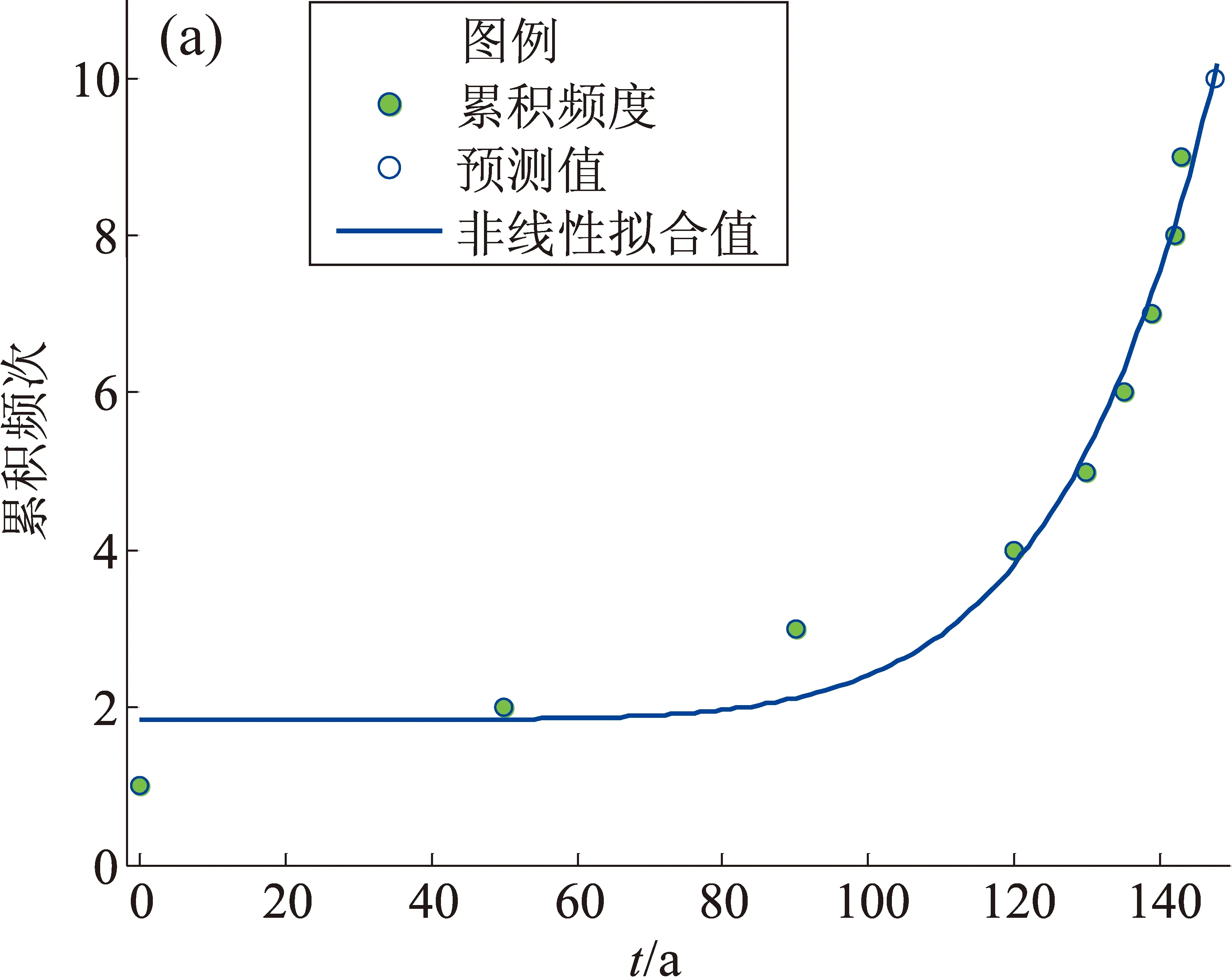
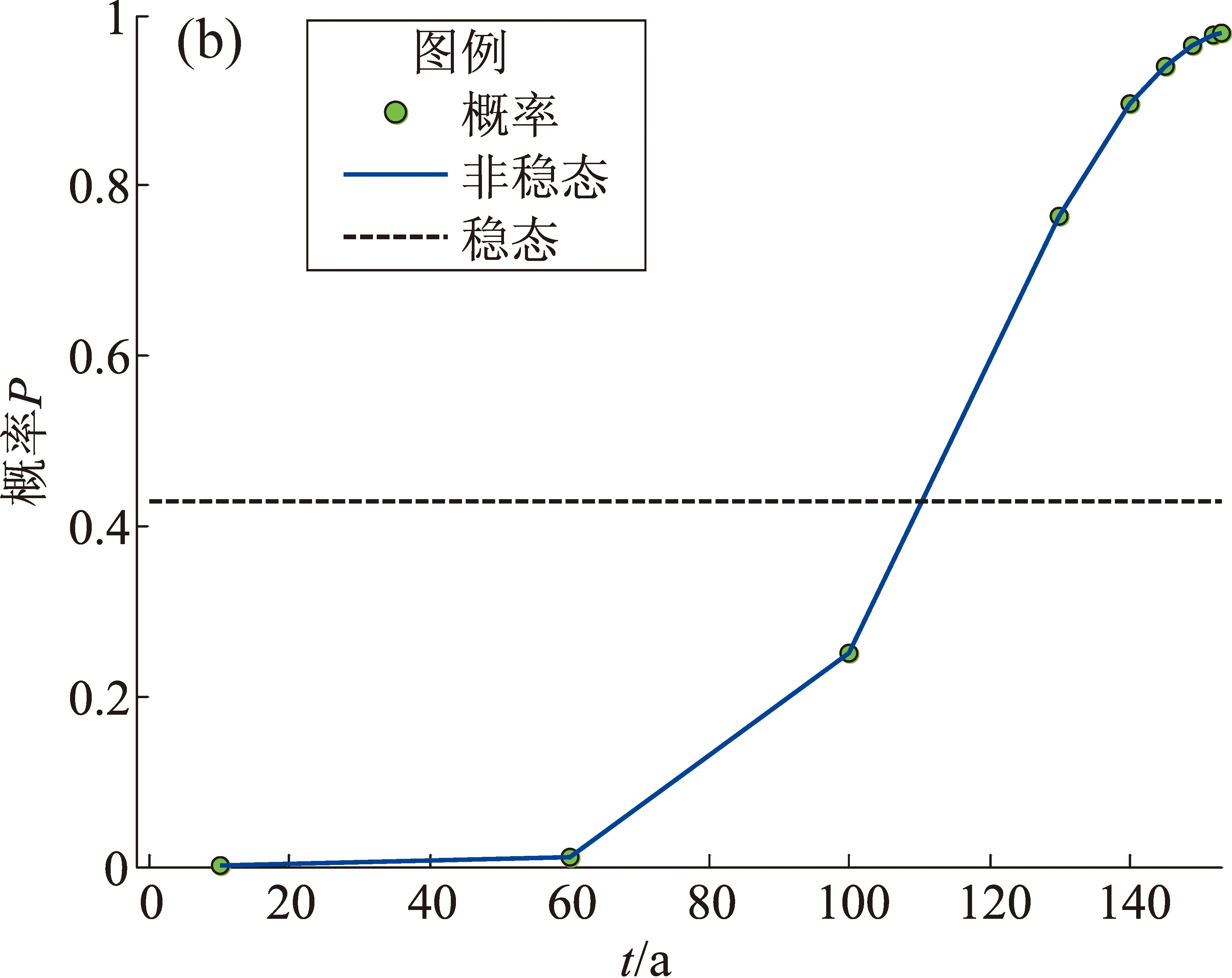
圖3 地震事件時間間隔逐漸減小情況下累積頻次(a)和概率(b)Fig.3 Cumulative frequency and probability with decreasing time interval of earthquake events
3 云南地區地震發生概率
3.1 研究資料
云南地區(20.5°~29.3°N,97.2°~106°E)M≥6.0地震在空間分布上極不均勻,主要沿活動斷裂展布,尤其是沿有較強活動水平的深大斷裂分布。根據云南地區M≥6.0地震的地震活動重復性、地震類型特征與地質構造關系,皇甫崗等(2010)將M≥6.0地震劃分為9個主要地震帶(區),如圖4所示。1900—2019年,云南地區共發生M≥6.0地震95次,9個地震帶內有地震78次,占82%。若按云南省界統計,云南省內共有地震61次,僅有4次地震位于地震帶外,即云南省內93%的M≥6.0地震均處于這9個地震帶內。
3.2 地震帶地震危險性初判
取各個地震帶M≥6.0地震,若地震帶內地震活動相對較弱,可適當降低起始震級,如寧蒗—鹽源地震帶。根據式(6),對各地震帶地震序列進行非線性擬合,從擬合方程可以計算下一次地震應該發生時間t,如果t小于目前時間,表明理論計算的地震在過去就應該發生,但實際上卻未發生,表明地震發生的危險性較大。反之,如果計算得到的t值大于目前時間,表明理論計算的地震應該在將來發生,意味著地震發生的危險性相對較小。因此,通過計算一次地震的發震時間可以對地震危險性進行初步判斷。
表1給出云南9個地震帶參數及危險性概率結果,圖5給出云南各地震帶歷史地震M-t圖和累計頻度N-t圖及其非線性擬合曲線。假設截止時間一律為2019年12月31日,在圖5的M-t圖中用紅色虛豎線表示,在N-t圖中,分別給出了穩態和非穩態計算結果,紅色空心圓表示按非線性擬合得到的方程計算的下一次地震應該發生的時間,表1給出了具體計算參數。
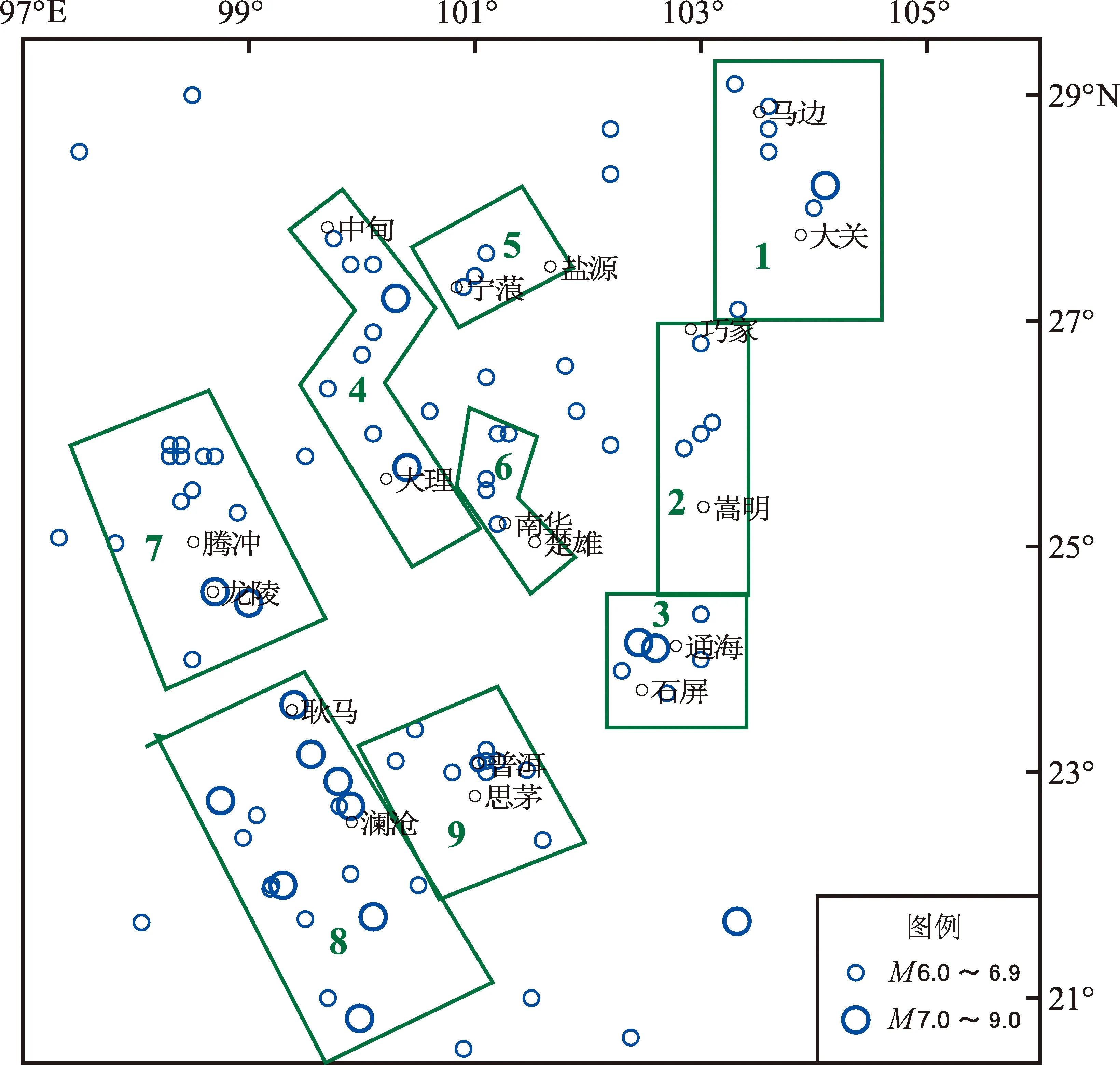
地震帶:1.馬邊—大關;2.小江;3.通海—石屏;4.中甸—大理; 5.寧蒗—鹽源;6.南華—楚雄;7.騰沖—龍陵; 8.瀾滄—耿馬;9.思茅—普洱
馬邊—大關地震帶發生M≥6.0地震7次,最后一次地震是2014年8月3日魯甸M6.5地震,預測的下一次地震應該發生在2039年,目前時間遠遠未到理論應發震時間,初步判斷該地震帶目前發生地震的危險性較小。
小江地震帶發生M≥6.0地震5次,最后一次地震是1985年4月18日祿勸M6.2地震,預測的下一次地震應該發生在2000年,目前時間遠遠超過理論應發震時間,初步判斷該地震帶目前發生地震的危險性較大。
通海—石屏地震帶發生M≥6.0地震7次,最后一次地震是1970年1月5日通海M7.8地震,預測的下一次地震應該發生在1988年,目前時間遠遠超過理論應發震時間,初步判斷該地震帶目前發生地震的危險性較大。
中甸—大理地震帶發生M≥6.0地震9次,最后一次地震是1996年2月3日麗江M7.0地震,預測的下一次地震應該發生在2008年,目前時間超過理論應發震時間,初步判斷該地震帶目前發生地震的危險性較大。
寧蒗—鹽源地震帶發生M≥5.5地震8次,其中6.0~6.9級地震3次,由于該地震帶6級以上地震較少,因此將該地震帶起始震級適當下降為5.5級,該地震帶最后一次地震是2012年6月24日寧蒗M5.7地震,預測的下一次地震應該發生在2032年,目前時間遠遠未到理論應發震時間,初步判斷該地震帶目前發生地震的危險性較小。
楚雄—南華地震帶發生M≥6.0地震5次,最后一次地震是2009年7月9日姚安M6.0地震,預測的下一次地震應該發生在2014年,目前時間超過理論應發震時間,初步判斷該地震帶目前發生地震的危險性較大。
騰沖—龍陵地震帶發生M≥6.0地震14次,最后一次地震是2014年5月30日盈江M6.1地震,預測的下一次地震應該發生在2028年,目前時間未到理論應發震時間,初步判斷該地震帶目前發生地震的危險性較小。
瀾滄—耿馬地震帶發生M≥6.0地震17次,其中7級以上地震多達8次,是云南地區7級以上大地震最容易發生的地震帶,該地震帶最后一次地震是2011年3月24日中緬交界M7.2地震,預測的下一次地震應該發生在2018年,目前時間略超過理論應發震時間,初步判斷該地震帶目前存在發生地震的危險性。
思茅—普洱地震帶發生M≥6.0地震11次,無7級以上地震,該地震帶是云南地區6級地震最集中的地震帶,最后一次地震是2014年10月7日景谷M6.6地震,預測下一次地震應該發生在2022年,目前時間未達到理論應發震時間,初步判斷該地震帶目前發生地震的危險性小。
從以上分析可以得知,假定未來地震的發展趨勢遵循歷史演化規律,則可以用計算的下一次地震發生時間的方法對未來地震進行定性判定,但無法進行定量描述,只能對地震危險性進行初步判斷。從表1還可以看到,計算的下一次地震發生時間的誤差還是較大的,誤差最大達26年,大多數誤差在8年以內,誤差偏大的主要原因是樣本的時間跨度長而樣本數又不多。如果簡單按照計算得到的下次地震理論計算時間從小到大排序,可初步將云南地震帶地震危險性的危險程度從高到低排列如下:通海—石屏地震帶、小江地震帶、中甸—大理地震帶、楚雄—南華地震帶、瀾滄—耿馬地震帶、寧蒗—鹽源地震帶、思茅—普洱地震帶、馬邊—大關地震帶。
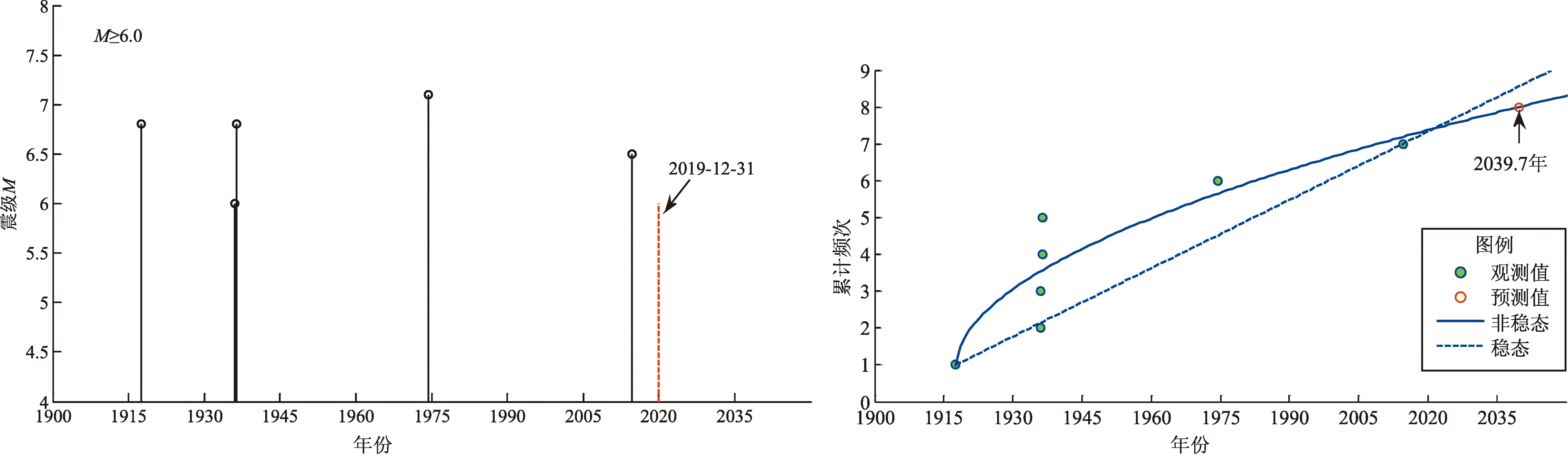
(a)馬邊—大關地震帶
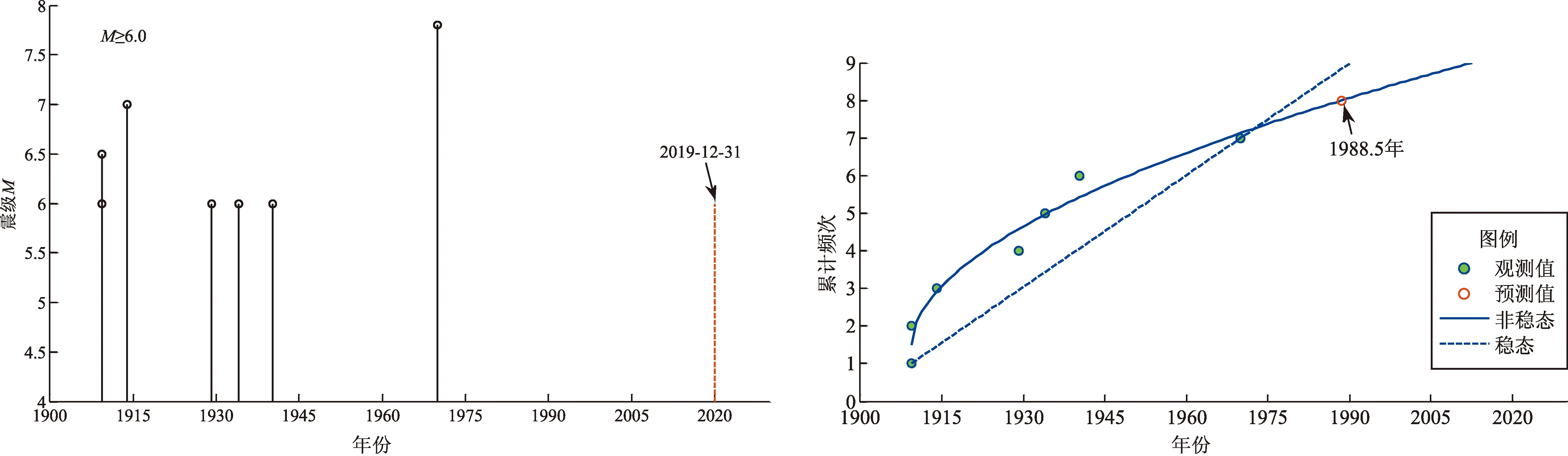
(c)通海—石屏地震帶
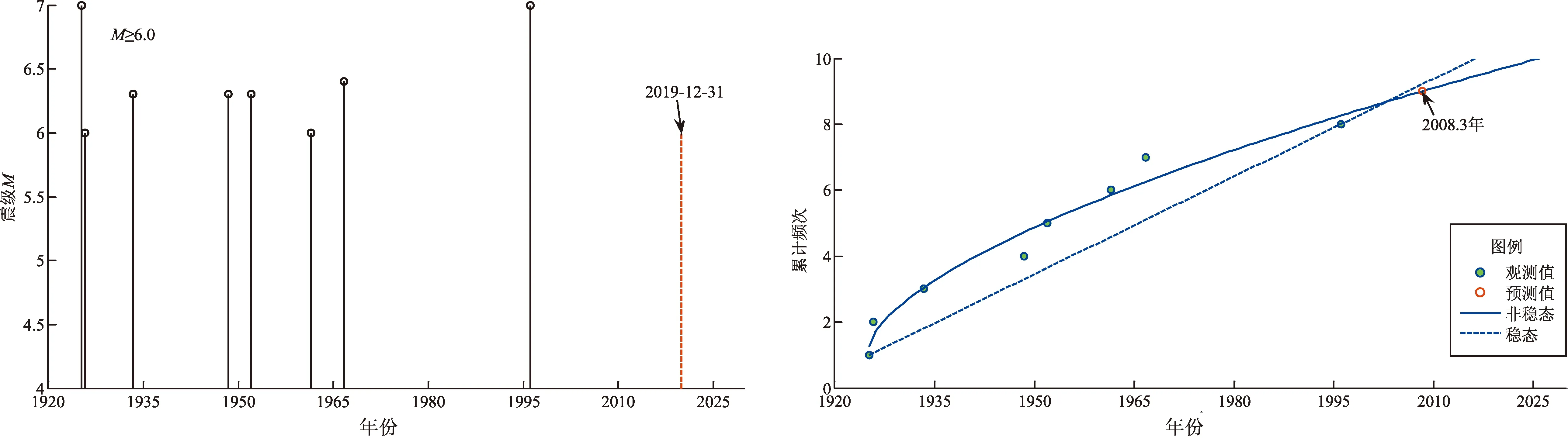
(d)中甸—大理地震帶

(e)寧蒗—鹽源地震帶
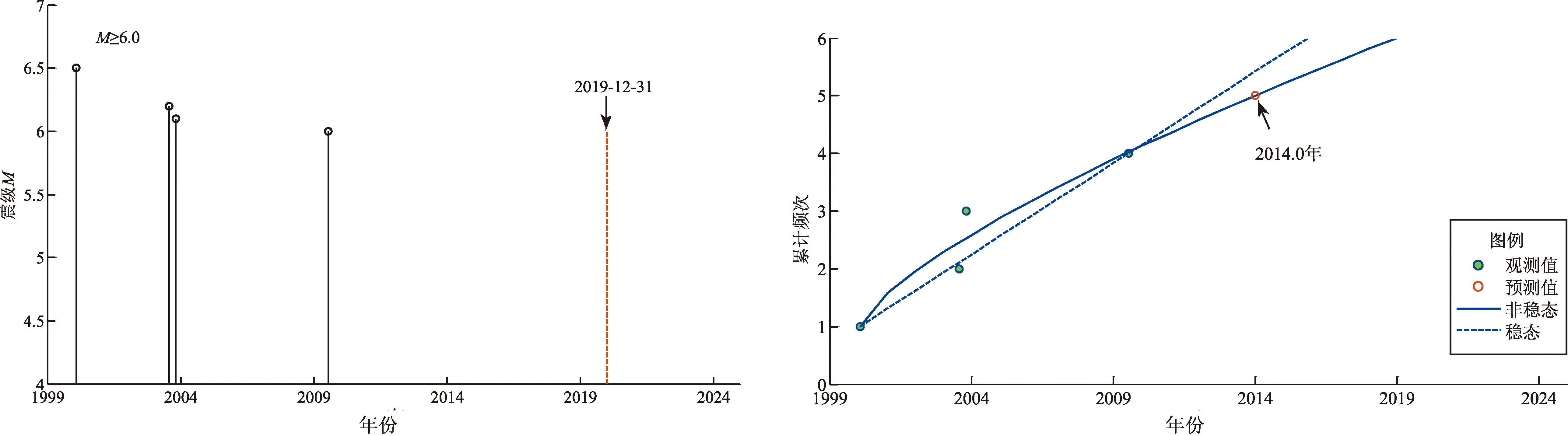
(f)楚雄—南華地震帶
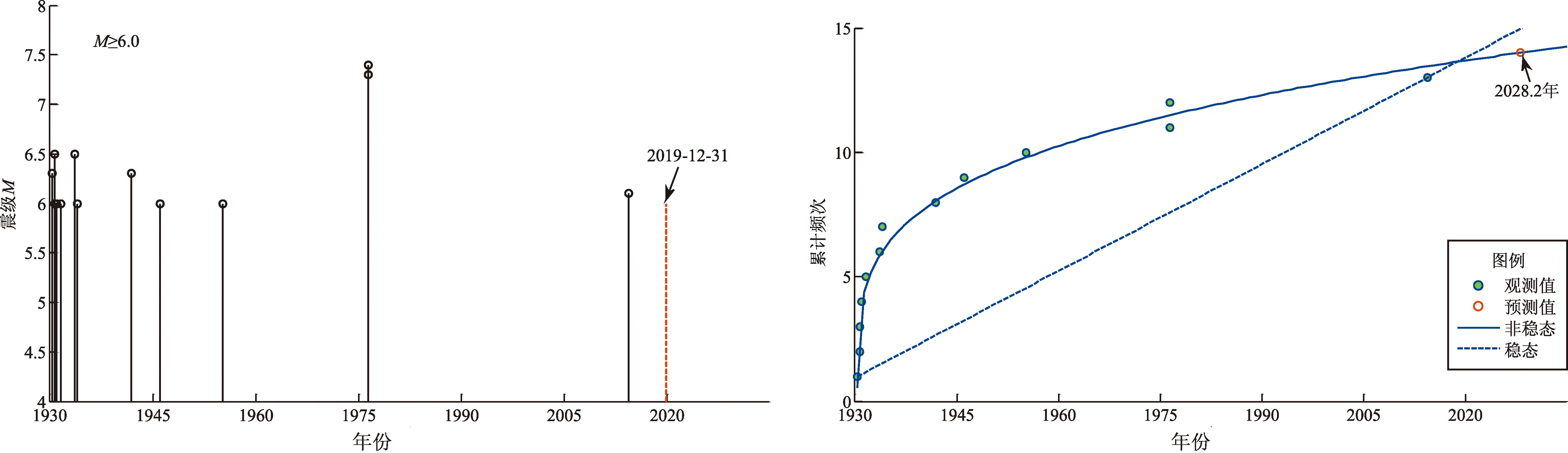
(g)騰沖—龍陵地震帶
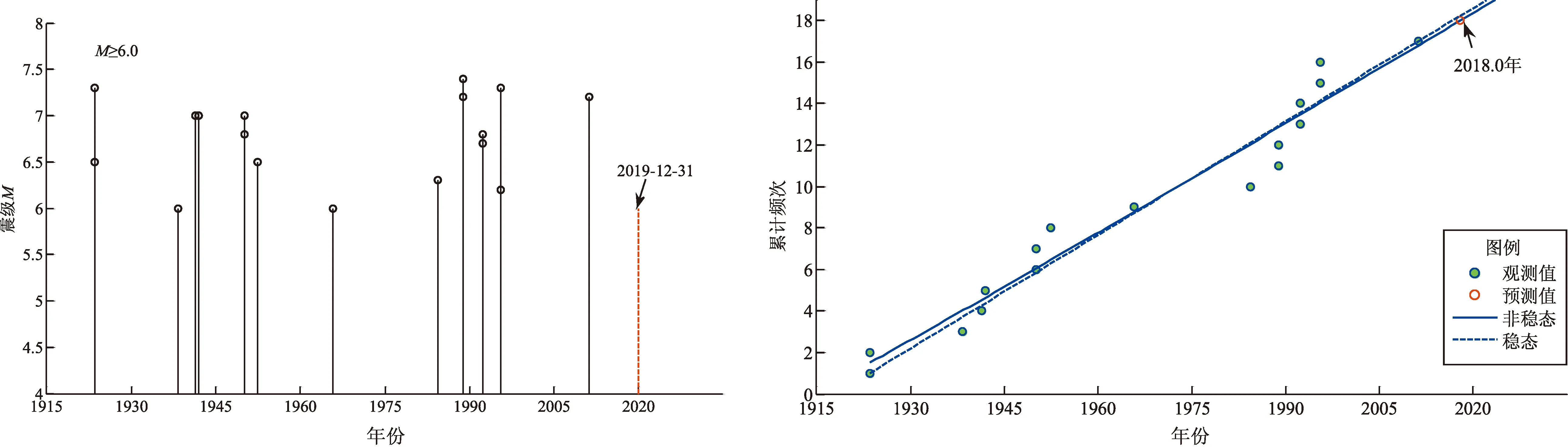
(h)瀾滄—耿馬地震帶
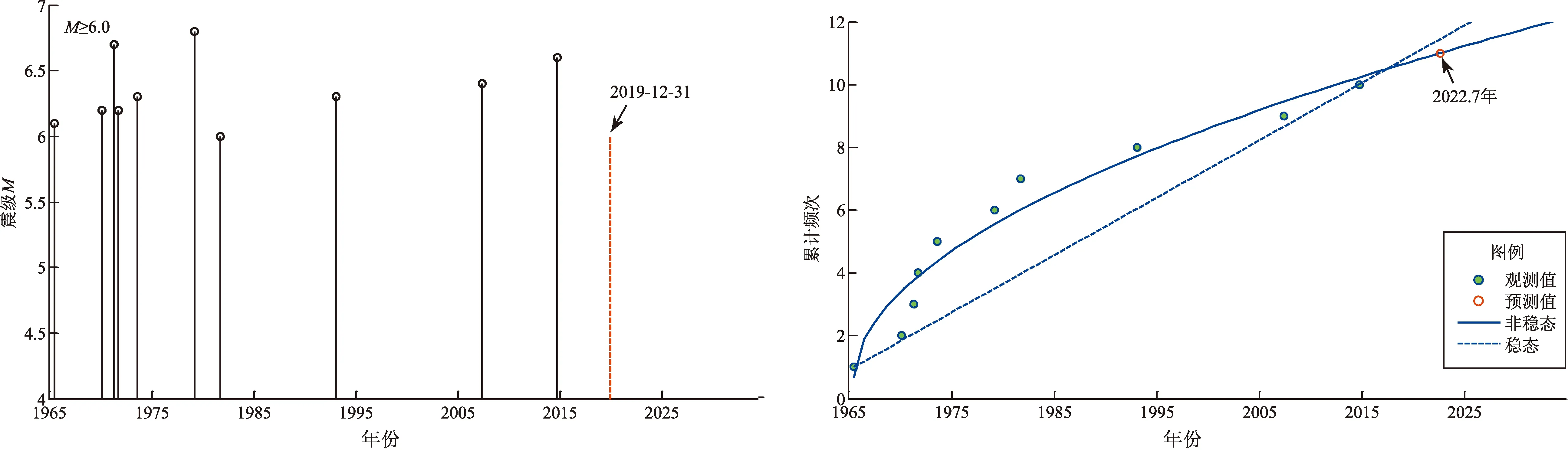
(i)思茅—普洱地震帶
3.3 地震帶理論概率
利用基于非穩態泊松分布的概率模型來對地震帶地震危險性進行定量判定。假定t0時刻發生一次地震,則在[t0,t0+t]時段內至少發生一次地震的概率可以用式(9)計算,在本文的研究中,統一取2019年12月31日為截止時間,以式(9)計算2019年12月31日以后tp=1年各地震帶至少發生1次地震的概率,tp為預測時間,因此,式(9)中時間t為最后一次地震到2019年12月31日的時間與預測時間tp之和,引入截止時間能使要計算的地震的時間概念清楚。對各個地震帶的預測統一為相同時間tp=1年,否則若以t0為基準,由于各地震帶有不同t0,計算的未來地震發生的時間就不相同。
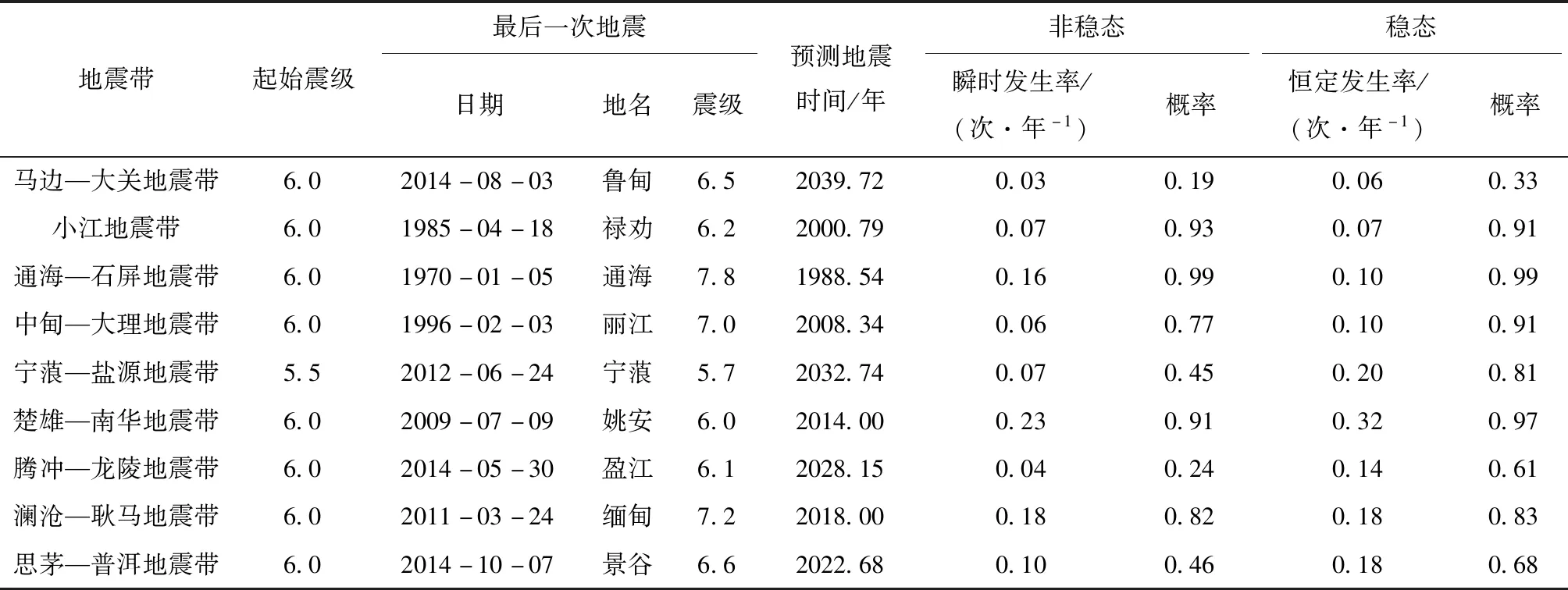
表1 云南地震帶地震發生的理論概率Tab.1 Theoretical probability of earthquake occurrence in Yunnan seismic belt
根據上述規定,從表1及圖5可見,云南各個地震帶的強震序列,以時間間隔逐漸增長和時間間隔無規律2種過程居多,未發現序列時間間隔逐漸減小過程,小江地震帶累積頻度隨時間呈非線性增長,但增長幅度不大(圖5b),在這種情況下非穩態概率大于穩態概率;瀾滄—耿馬地震帶累積頻度隨時間呈線性增長(圖5h),非穩態概率與穩態概率大致相同;大部分地震帶累積頻度隨時間呈非線性減小,非穩態概率小于穩態概率。從圖5還可以看到,曲線向下彎曲越多非穩態概率和穩態概率相差越大,如寧蒗—鹽源、騰沖—龍陵、思茅—普洱地震帶。
圖6a給出云南各地震帶非穩態泊松分布的概率模型預測未來tp=1年地震發生理論概率,從圖中可以看到,理論概率最高的地震帶為通海—石屏地震帶、小江地震帶和楚雄—南華地震帶,中甸—大理地震帶和瀾滄—耿馬地震帶次之,其它地震帶理論概率較小,這個結果與本文根據計算下次地震發震時間做出的初步危險性判定結果一致。
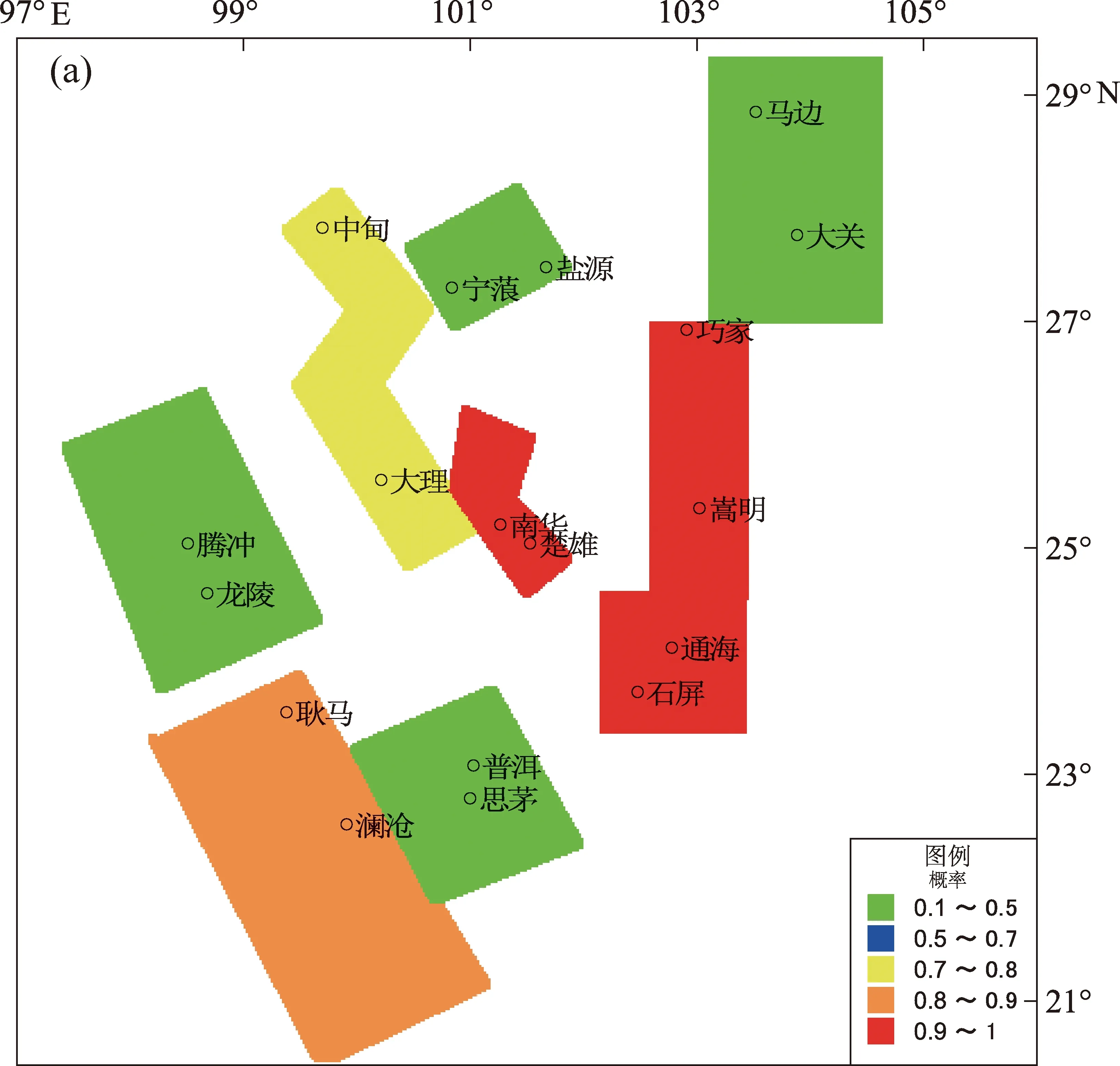
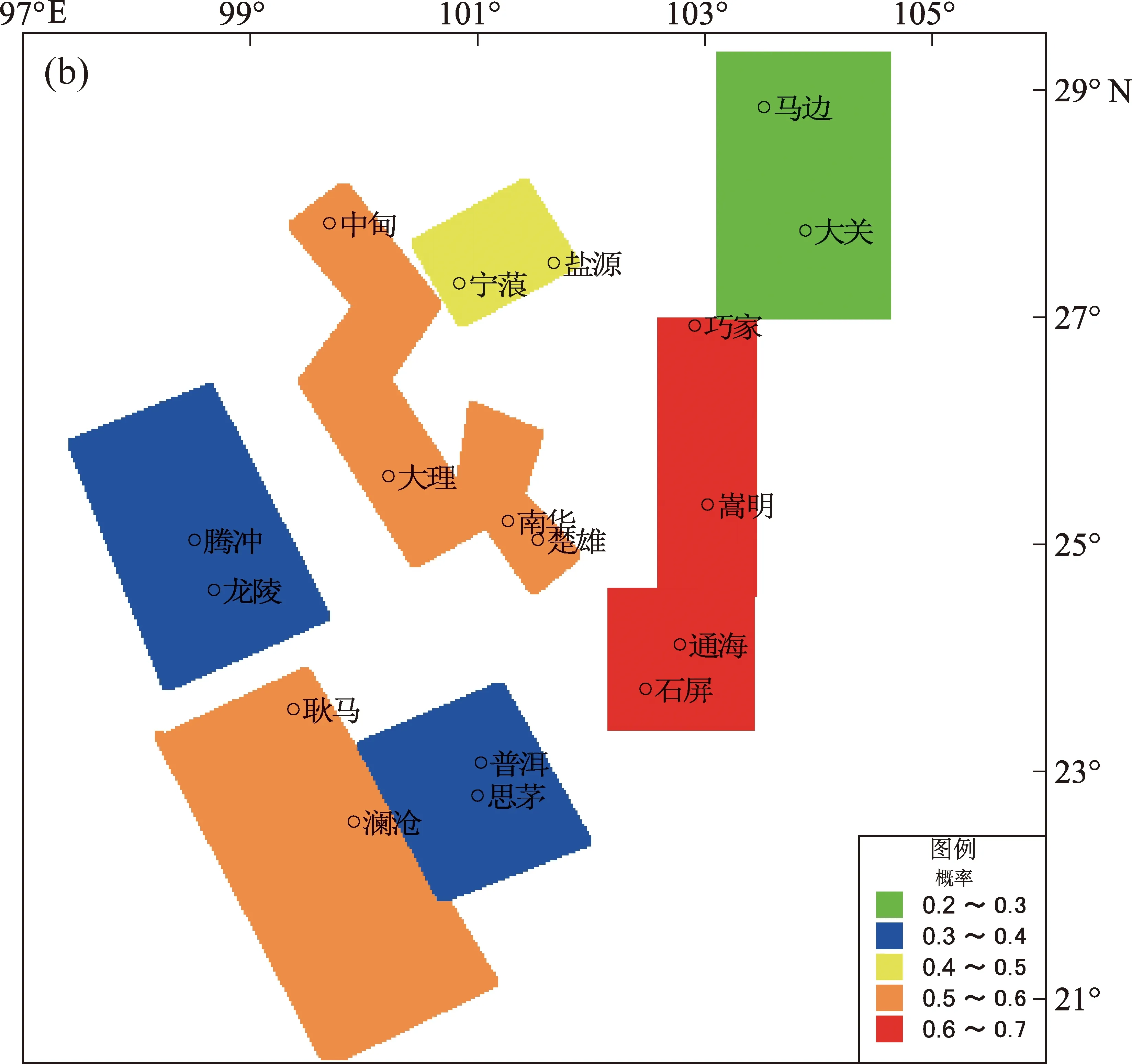
圖6 云南地震帶理論概率(a)和綜合概率(b)Fig.6 Theoretical probability and synthetical probability of Yunnan seismic belt
3.4 地震帶綜合概率
表1僅給出根據非穩態泊松分布的概率模型計算的理論概率值,一些因素對預測結果存在影響,需要在理論計算的基礎上進行綜合考慮。從表1可以看出,一些地震帶地震的預測時間比目前時間早,即按理論計算地震應該已經發生,但實際上還未發生,表2給出目前至預測地震的時間間隔(Y3)參數,當Y3為正數時表示預測時間提前,這種情況涉及到小江地震帶、通海—石屏地震帶、中甸—大理地震帶、楚雄—南華地震帶和瀾滄—耿馬地震帶,其中小江地震帶、通海—石屏地震帶和中甸—大理地震帶預測提前的時間較多。整體來看,以下一些因素可能對地震預測造成影響:
(1)時間間隔。這是單純利用平靜時間來預測地震的危險程度,平靜時間越長發震的可能性就越大,表2給出目前至預測地震的時間間隔(Y3)參數,Y3越大平靜時間越長,在綜合考慮預測結果時,對時間間隔這一因素,認為Y3越大,對綜合概率P的貢獻越大。
(2)預測精度。從圖5看到,實際值與理論預測值的誤差越小,預測的信度越高,使用平均絕對百分比誤差MAPE來衡量預測精度:
(10)
式中:yi,i分別為預測對象的實際值和預測值。表2中給出了各地震帶的MAPE值(Y2),絕大多數在15%以內,馬邊—大關地震帶、小江地震帶和思茅—普洱地震帶誤差偏大。因此,在綜合考慮預測結果時,對預測精度這一因素,認為MAPE值越小,對綜合概率P的貢獻越大。
(3)最后地震的震級。某地區發生較大地震后再次發生地震的時間一般比相對較小地震后平靜的時間要長,即大地震后能量釋放較為徹底,需要更長的時間來進行能量積累。上文提到一些地震帶理論計算的地震早應該發生,但實際卻沒有發生,從這些地震帶的最后地震震級來看,目前至預測地震的時間間隔(Y3)較長的地震帶為小江地震帶、通海—石屏地震帶和中甸—大理地震帶,后2個地震帶最后地震震級均大于等于7級,地震后實際平靜時間超出理論值可以用能量積累需要更長時間來解釋。表2給出各地震帶最后地震震級(Y4),在綜合考慮預測結果時,對最后地震震級這一因素,認為震級M越小,對綜合概率P的貢獻越大。
(4)資料長度。從圖5可以看到,由于各地震帶地震活動水平和歷史地震記錄完整性不同,資料的使用時間長度是不同的,資料的時間越長越能較全面反映該地區地震活動狀態,預測信度也越高,表2給出各地震帶資料長度(Y5),在綜合考慮預測結果時,對資料長度這一因素,認為資料越長,對綜合概率P的貢獻越大。
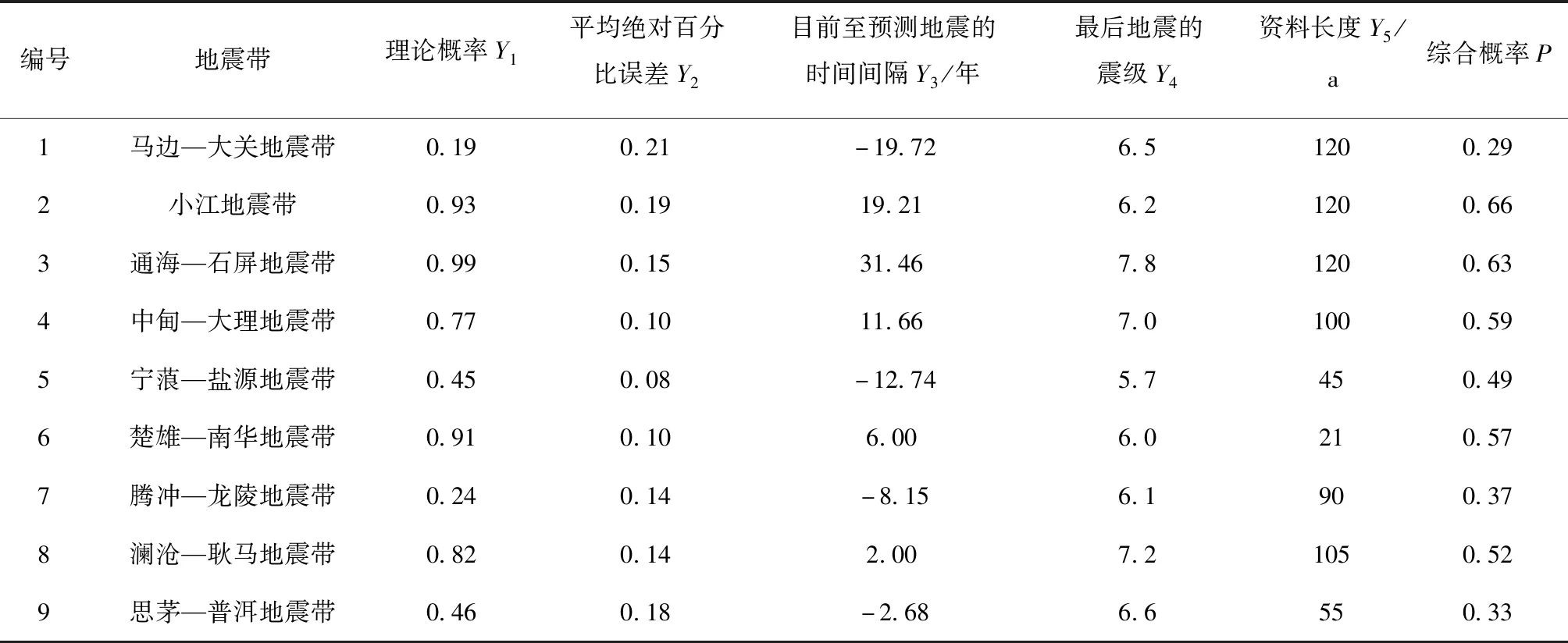
表2 云南地震帶綜合概率Tab.2 Synthetical probability of earthquake occurrence in Yunnan seismic belt
由于目標是考慮諸多因素對理論計算概率值的影響,假設各個因素(或單項)對綜合概率P的總貢獻(或權重ω)為1,則理論概率(Y1)的權重ω1應大于Y2~Y5各單項權重,Y2~Y5各項取等權重。因此,各權重可取為:
ωi=(ω1,ω2,ω3,ω4,ω5)=(0.3,0.15,0.15,0.15,0.15)
(11)
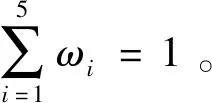
對表2中Y1~Y5各列進行歸一化處理(其中Y2,Y4先取倒數),利用權重集成法計算綜合概率P(陳立德,1993):
(12)
從表2的理論概率與綜合概率的變化可以看到,小江地震帶、通海—石屏地震帶和楚雄—南華地震帶理論概率較高,計算后綜合概率均出現一定減小,小江地震帶是由于誤差(MAPE)較大,通海—石屏地震帶是由于最后地震震級達7.8級,楚雄—南華地震帶是由于資料時間較短。馬邊—大關地震帶綜合概率出現一定增大,是由于Y3,Y5貢獻較多。從圖6b可以看到,小江地震帶和通海—石屏地震帶綜合概率相對較高,范圍為0.60~0.69,中甸—大理地震帶、楚雄—南華地震帶和瀾滄—耿馬地震帶綜合概率次之,范圍為0.50~0.59,其它地震帶綜合概率相對較小。
4 結論和討論
針對強震危險性概率預測問題,提出基于非穩態泊松過程的概率計算方法,通過穩態與非穩態模型對比研究發現,非穩態泊松模型隨時間而變化的地震發生率能更好地描述強震發生規律,利用非穩態泊松模型計算了地震發生的理論概率,發現理論概率受到預測精度、平靜時間、最近地震大小等諸多因素影響,利用權重集成法計算了強震發生的綜合概率。結果表明:①地震發生的累積頻度隨時間的非線性變化能用冪指數函數模型來描述;②基于非穩態泊松模型的地震發生率隨時間而變化,與地震發生率恒定不變的穩態模型相比,前者對地震活躍-平靜韻律狀態更加敏感;③對云南地區9個地震帶強震發生的綜合概率計算結果顯示,若以2019年12月31日為截止時間,小江地震帶和通海—石屏地震帶綜合概率較高大于0.6,其次為中甸—大理地震帶、楚雄—南華地震帶和瀾滄—耿馬地震帶,綜合概率范圍為0.5~0.59,其它地震帶綜合概率均小于0.5。
(1)假設本輪回的地震活動可能重演上一輪回的活動,這是利用非穩態泊松模型進行預測的基礎。如果一次地震發生后,無法判定地震活動輪回是否結束,則認為地震活動將延續之前活動過程。如果一次地震發生后能確定是輪回的結束,新的一個輪回即將開始,則將上一次輪回過程結束的時間作為下一次輪回的開始,因此作為輪回開始和輪回進行中得到的概率是不同的,在計算概率之前需要先對輪回過程進行判定。
(2)當地震序列呈現加速增長時,非穩態泊松過程序列初期的地震發生率要低于整個全過程平均發生率(即穩態泊松過程發生率),之后非穩態發生率將隨時間增大,尤其是到后期增加較快。當地震序列隨時間呈現大幅減小時,地震活動加速增長。反之,當地震序列時間間隔逐漸增加時,初期發震率較高,越到后期發震率越小。當地震序列呈線性均勻增長時,序列各個時期的地震發生率與整個全過程平均發生率相當。
(3)本文認為地震事件累積頻度N隨時間t呈冪指數增長,這種冪指數增長模式大量存在于自然現象中,蔣海昆等(2009)進行巖石破裂聲發射實驗時,發現巖石材料在受壓破壞之前聲發射的強度隨時間呈冪指數增長(或減小)模式;秦嘉政和錢曉東(2004)研究了云南地區30次中強地震震前應變釋放現象,發現地震應變能隨時間呈冪指數增長(或減小)模式變化;蔣長勝和吳忠良(2009)對中國大陸109例M≥5.7地震進行地震矩研究,也發現地震矩釋放隨時間呈冪指數增長(或減小)變化;本文得到的地震事件累積頻次隨時間呈冪指數增長現象,可能反映了地震現象的某種規律。
(4)式(6)中常數b是重要參數,它是地震發生快慢程度的反映,當b>1時,累積頻度隨時間曲線為加速形態,表示事件時間間隔Δt遞減,隨時間的增長地震事件發生愈多,發生率增大,事件發生概率增大。當b>1時,曲線為減速形態,表示事件的時間間隔Δt遞增,隨時間的增長地震事件發生愈少,事件發生率減小,發生概率減小,上述2種情況為非穩態泊松分布,適用于大量地震活動具有非均勻分布的地區。當b=1時,曲線為直線形態,表示事件時間間隔Δt呈無規則分布,隨時間增長地震事件發生的數目不變,同時事件發生率和發震概率也不變,這種情況為穩態泊松分布,適用于一些地震活動相對均勻的地區。
(5)統計結果與樣本、區域、時段、方法密切相關,不同的統計對象會給出不同結果,尤其在做長時間歷史地震統計分析時,一定要考慮歷史地震可能存在的遺漏現象,尤其是7級以下地震,因此在具體分析預測中應注意到這些情況。

