基于神經網絡和知識庫的物料配送動態調度

周炳海 朱柘鑫

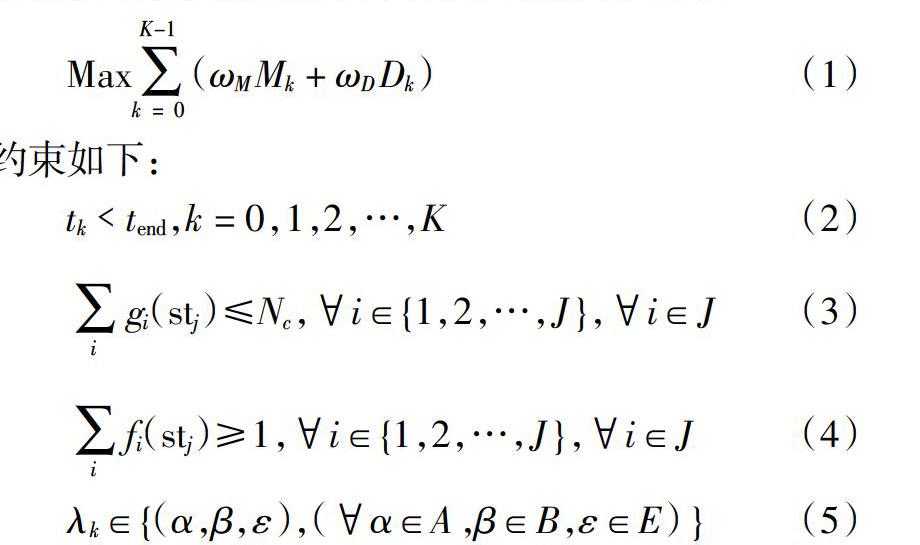
摘? ?要：為有效地解決汽車混流裝配線中多載量小車物料配送的動態調度問題，提出基于知識庫和神經網絡的調度方法. 首先，對汽車裝配線物料配送的動態調度問題進行描述，建立以裝配線產量和多載量小車的物料搬運距離作為衡量指標的目標函數. 然后通過Plant Simulation軟件生成針對汽車混流裝配線的仿真數據并對神經網絡模型進行離線訓練，在實時階段利用神經網絡模型和知識庫實現多載量小車最優調度規則的選取. 實驗結果表明：所提出的調度規則選取方法選擇的調度規則大多為最優調度規則，以較低的調度規則計算復雜性確保了調度的實時性能，能夠很好地應對動態環境的變化，從而有效提升了多載量小車的動態調度水平.

關鍵詞：汽車混流裝配線;動態調度;物料搬運;神經網絡;人工智能

中圖分類號：TP391? ? ? ? ? ? ? ? ? ?文獻標志碼：A

Abstract：In order to tackle the dynamic scheduling problem of tow trains in mixed-model assembly lines， a scheduling approach is proposed based on the knowledge base and neural network. Firstly， the dynamic scheduling problem of material delivery in the automotive assembly line is formally described. The throughput of the assembly line and the total delivery distances are selected as components of the objective function. After that，the sample data of mixed-model assembly lines are generated by the Plant Simulation software and are used to train the neural network model offline. Finally， the trained neural network model and the knowledge base are adopted in the real-time scheduling process to select the optimal scheduling rule for tow trains. The experimental results indicate that the scheduling rules selected by the selection method proposed in the paper are mostly the optimal ones. The lower computational complexity of scheduling rules ensures the real-time performance of scheduling. It can cope well with changes in the dynamic environment， thus effectively improving the dynamic scheduling of tow trains.

Key words：mixed-model assembly line;dynamic scheduling;material handling;neural network;artificial intelligence

隨著產品與客戶需求復雜化、市場多樣化等競爭壓力的不斷增加，汽車制造企業多采用多載量小車（tow train）進行物料配送[1]，提升多載量小車的動態調度水平，實現汽車混流裝配線的準時化物料配送，已成為降低汽車制造企業成本的有效措施之一.

制造系統中的物料配送調度問題通常分為靜態與動態兩個方面[2]. 靜態調度指假定在調度前已知所有物料搬運需求，通過運籌學等決策分析方法解決調度的最優化問題. 其中啟發式算法以其求解較大規模問題的時間優越性，近年來受到國內外學者的廣泛關注. Emde等[3]提出了開放式啟發算法及禁忌搜索算法來解決電動小車（Electric Vehicle，EV）廠內循環的物料準時配送問題;文獻[4-6]以最小化汽車裝配線線邊庫存和配送次數為目標，研究了物料配送中多載量小車的裝載和調度問題，分別提出了基于模擬退火的啟發式算法、基于蟻群優化的啟發式算法以及改進型粒子群算法.

雖然上述靜態調度方法在中大問題規模中能夠找到近似最優解，但因其對于制造系統較差的抗干擾性，致使該方法難以應用到實際物料搬運系統的調度中，因此動態調度得到越來越廣泛的關注[7]. 其中，機器學習（Machine Learning，ML）作為人工智能的重要分支被廣泛應用于動態調度中. 文獻[8]和文獻[9]均將遺傳算法與人工神經網絡（Artificial Neural Network，ANN）相結合來解決制造系統中的動態調度問題，并證明了混合算法的有效性與優越性. Zang等[10]開發出一種混合深度ANN調度器，利用其泛化能力處理車間中的調度問題. 文獻[2]提出了一種基于支持向量機的方法對多載量小車是否執行搬運任務做出決策.

上述文獻主要研究了制造系統中資源分配和派遣決策等問題，對于多載量小車在汽車裝配線中搬運任務的動態選擇與排序決策問題鮮有涉及. 因此，本文利用神經網絡出色的學習能力以及預測準確性[11-12]，結合知識庫，引入果蠅優化算法（Fruit Fly Optimization Algorithm，FOA）[13]與廣義回歸神經網絡（General Regression Neural Network，GRNN）[14]，以裝配線產量和多載量小車的物料搬運距離作為衡量指標建立數學模型，提出了針對多載量小車的最優調度規則動態選取方法，有效地解決了小車的發車決策、物料配送任務選擇決策與物料配送任務排序決策問題.

1? ?問題描述與模型建立

1.1? 問題描述

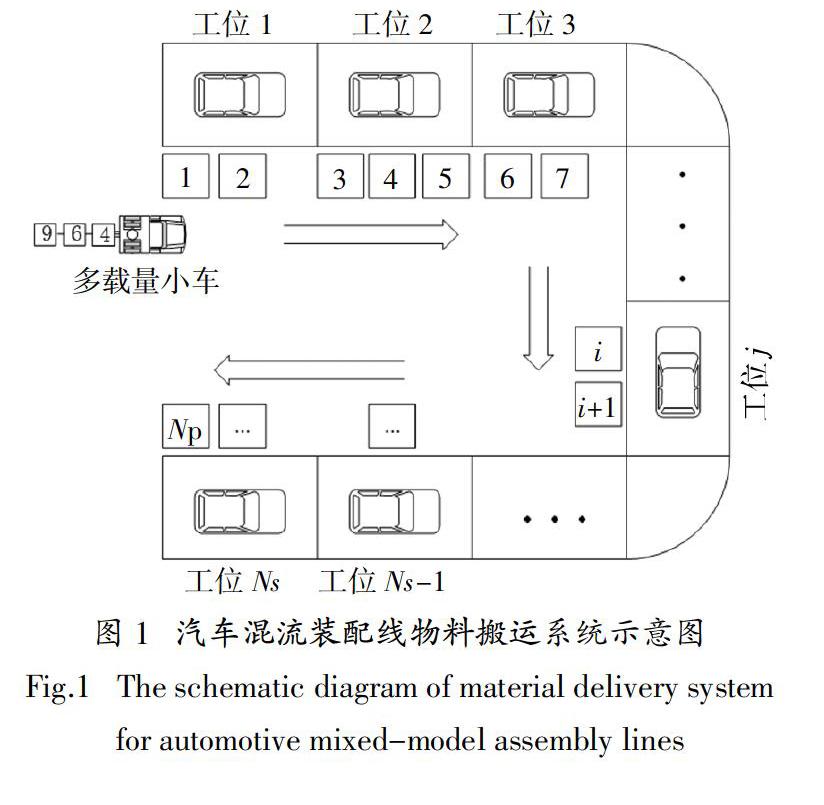
圖1展示了汽車混流裝配線的物料搬運系統，暫存于物料超市中的物料由一輛或多輛多載量小車多批次、小批量地送至臨近工位. 本文對于多載量小車的動態調度包含以下3方面的決策問題：

1）發車決策問題.當多載量小車位于零件庫存區處于“空閑”狀態時，調度系統需要決定多載量小車何時處理搬運任務，出發進行物料配送. 最小批量法（Minimum Batch Size rule，MBS-x）[12]為解決此類問題的一個經典規則，表示只有在當前需要執行的搬運任務數量超過最小批量x時，多載量小車才開始出發執行配送任務，否則一直在物料超市等候.

2）物料配送任務選擇決策問題.即調度系統做出讓多載量小車發車的決策后，如果配送任務的數量超出多載量小車的搬運能力Nc，那么調度系統就需要選擇搬運任務進行物料配送.

3）物料配送任務排序決策問題.若調度系統在物料配送任務選擇決策中選擇了多于一個配送任務，由于本文所述的多載量小車受LIFO約束，所以調度系統必須在搬運過程開始前確定所有零件的配送次序.

由于針對不同的決策問題可以采用相應的調度規則，因此在解決本文的多載量小車動態調度問題時，可在已有的針對各決策問題的調度規則中尋找合適的調度規則組合.

令λ = （α，β，ε），（?α∈A，β∈B，ε∈E）表示上述的調度規則組合，其中α、β、ε表示分別用于發車決策問題、物料配送任務選擇決策問題以及物料配送任務排序決策問題的調度規則，A、B、E分別為對應決策問題的調度規則集. λ = （MBS-2，FRFP，SDFD）表示如果搬運任務數量不少于2，那么多載量小車開始執行搬運任務;如果當前搬運任務數量超出多載量小車的搬運能力，它將使用先訂購先選擇規則（First Reorder First Picked，FRFP）選取搬運任務;最后，在選擇了多個搬運任務的情況下，它將使用（Shortest Distance First Delivered，SDFD）規則確定這些任務的搬運次序. 令Λ = {（α，β，ε），（?α∈A，β∈B，ε∈E）}表示存儲這種調度規則組合的調度規則集.

1.2? 數學模型

為簡化此類調度問題，做出如下基本假設：

1）多載量小車在搬運過程中行駛速度v恒定，且不考慮故障或阻塞問題;2）多載量小車由一輛牽引車頭和多輛送料車組成，一輛送料車一次只能裝載一種零件，且數量一定，記為SPQ（Supply Quantity），對于每種零件，多載量小車每次最多使用一輛送料車;3）空閑的多載量小車在裝配線由于缺少零件而停止裝配時，立即從物料超市出發執行配送任務;4）多載量小車的裝料時間LDT（Loading Time），卸料時間UDT（Unloading Time）（卸料時剩余零件的數量≤0.1SPQi）和UDT′（卸料時剩余零件的數量>0.1SPQi）都為定值，且UDT′ > UDT;5）搬運過程不可中斷;6）采用再訂購點法作為物料搬運任務生成的方法.

為深入分析問題并進行模型表述，對相關符號及變量定義如下：

裝配線可進行M1，M2，…，MH種型號的車輛裝配，產品配比m = （ρ1，ρ2，…，ρH），ρ1 + ρ2 +…+ ρH = 1;裝配過程需要的零件記為Pi（i = 1，2，…，I）;物料搬運的開始時間為t0;調度的終止時間為tend;調度系統在第k個決策點tk（k = 0，1，2，…，K）時刻，產品配比mk = （ρ1，ρ2，…，ρH）或調度目標權重ωk = （ωM，ωD）發生變化，調度策略需重新調整，其中ωM和ωD分別為裝配線產量M 和多載量小車的行駛距離即物料搬運距離 D的權重，且ωM>>ωD;bk = （Mk，Dk）為調度期間[tk，tk+1]中的調度性能，其中Mk、Dk分別為調度期間[tk，tk+1]中的裝配線產量和物料搬運距離;IL（i，t）為零件Pi在時刻t的線邊庫存;csi為零件Pi的平均消耗速度;Pi的再訂購點Ri =csi[（di + 2dmax）/v + Nc（LDT + UDT）]，其中di、dmax分別為搬運零件Pi的行駛距離及最遠行駛距離;在t時刻，若系統發出Pi的搬運需求，則fi（t） = 1，否則fi（t） = 0;在t時刻，若Pi被選中作為即將開始搬運的零件類型，則gi（t）=1，否則gi（t） = 0;stj為第j次搬運開始的時刻;J為多載量小車在[t0，tend]中所有的物料搬運過程.

由于本文選取裝配線產量和多載量小車的物料搬運距離這兩個有沖突的衡量指標建立目標函數，因此引入調度目標權重ωk=（ωM，ωD），產量的目標ωM 取正值表示產量越高，調度性能越好;物料搬運距離的目標權重ωD取負值表示距離越長，調度性能越差. 根據權重和的標量化方法，調度目標函數為：

式（1）為該調度模型的目標函數，表示最大化整個調度期間的產量和物料搬運距離的標量化權重和;式（2）表示調度系統的每個調度決策時刻都應早于調度期間的結束時刻;式（3）表示多載量小車每次搬運過程中裝載的料箱數不超過它的搬運能力;式（4）表示多載量小車在每次搬運任務執行前都收到不少于一個搬運任務;式（5）表示所有的調度規則組合都從備選調度規則集中選取.

2? ?動態調度方法

當產品配比和調度目標權重發生變化時，系統采取不同的調度規則會有不同的性能表現[13]，調度性能在所有條件下都最佳的調度規則并不存在. 因此，當動態環境中的產品配比或調度目標權重發生變化時，為了解決本文物料配送系統的動態調度問題，從給定的調度規則集中選擇一個使當前裝配線調度性能呈最優的調度規則是可行方案.

由于裝配線在整個調度期間的調度性能（產量和物料搬運距離）是由產品配比、調度規則及總生產時間決定的，與調度目標權重無關，因此假定總的生產時間以及相關因素不變，調度性能與產品配比和調度規則之間的關系可以表示為（mk←λ）→（M，D）. 對于給定的一條裝配線，若各調度期間的產品配比為mk，物料搬運調度系統采用的調度規則為λ，則該裝配線的裝配產量預計為M，物料搬運距離預計為D. 假定存在一知識庫，對所有可能的產品配比以及調度規則的組合存儲上述關系，那么對于任意給定的產品配比或調度目標權重，都可通過檢索知識庫的數據記錄，選取最合適的調度規則λ. 然而，產品配比的值域是連續的，知識庫中不可能存儲全部產品配比所對應的關系式，并且在相等的裝配時長中，兩個相似的產品配比采取同一調度規則時會得到相似的裝配線產量和物料搬運距離. 因此，對于任意未存儲在知識庫中的給定產品配比mk，可先在知識庫中找到與mk最相似的產品配比m，然后利用知識庫確定mk在調度目標權重ωk條件下的最優（即使目標函數最大）λ，作為mk在ωk條件下的最優調度規則λk.

為更好地實施上述方案，鑒于由輸入層、模式層、求和層和輸出層構成且執行Parzen非參數估計的GRNN具有良好的非線性逼近性能和訓練方便性，本文提出了一個基于知識庫和邏輯混沌初始化的果蠅優化算法（VSCFOA）改進型GRNN調度規則選取方法（VSCFOA-GRNN），如圖2所示，其中VSCFOA主要用來優化GRNN平滑因子. 主要包括離線VSCFOA-GRNN訓練和基于VSCFOA-GRNN實時決策兩個階段. 在離線訓練階段，調度系統通過仿真獲取調度性能指標（產量和物料搬運距離）與產品配比和調度規則之間的關系，構建一個存儲此關系的知識庫并訓練VSCFOA-GRNN神經網絡;在實時決策階段，調度系統通過神經網絡選取與當前給定的產品配比mk最相似且存儲于知識庫中的產品配比m′，檢索知識庫中記錄有關調度性能記錄數據，找出使得目標值最大的調度規則λ*，即為最優調度規則.

2.1? ?離線VSCFOA-GRNN神經網絡訓練

2.1.1? ?VSCFOA-GRNN的構建

在離線階段，由于相似的產品配比在使用同一調度規則時使得裝配線呈現相似的調度性能，所以可根據不同產品配比條件下的裝配線性能來定義產品配比之間的相似程度：

式中：mk為需要匹配的產品配比;mall為知識庫中存儲的所有產品配比的集合;為了提高匹配效率，可以將產品配比的搜索范圍縮小至mk的θ范圍;δ（mk，m）為mk與m的歐氏距離，即在歐氏空間中兩點的真實距離.

由式（6）和式（8）可知，為了計算兩個產品配比間的相似度從而進行相似性檢索，首先需要確定函數，但由于制造系統中產品配比和調度性能間的復雜關系，qλ（mk）的表達式很難準確地給出. 在這種情況下，鑒于廣義回歸神經網絡較強的非線性映射能力與果蠅優化算法的全局尋優能力，本文采用VSCFOA-GRNN對qλ（mk）函數進行逼近. VSCFOA算法通過混沌搜索找到初始最優值，利用步長找到最優味道濃度判定值Si，將Si作為GRNN的平滑因子Spread，通過對GRNN的訓練得到輸出值，計算輸出值與目標值之間的均方誤差MSE，MSE的值越小，說明預測模型描述實驗數據的性能越好. 通過迭代尋找最優味道濃度值代入GRNN進行函數擬合. 具體步驟如下：

2.1.2? ?知識庫的構建

為了得到相應產品配比與調度規則對應裝配線調度性能的關系式，通過Plant Simulation建立了針對裝配線物料搬運系統的仿真模型，如圖3所示.

該汽車裝配線共生產3種車型M1、M2、M3，仿真設19個裝配工作站S1 ～ S19，32種零件P1 ～ P32. 該裝配線上所有工作站的裝配周期為120 s，各工作站的平均失效間隔MTBF為56 min，平均修復時間MTTR為14 s. 多載量小車的數量為3，搬運能力Nc = 3，速度v = 1.48 m/s，LDT = 35.5 s，UDT = 46.6 s，UDT′ = 132.7 s. 將值域連續的產品配比m向量空間均勻離散化為s組不同的產品配比，每個產品配比 mi與不同的調度規則λj作為仿真模型的輸入獲得相應的裝配線產量Mij和物料搬運距離Dij作為仿真結果，并且將（mi λj Mij Dij）作為一組數據存入知識庫以備后續檢索.? ? 由于不同的λj會導致裝配線不同的性能表現，所以對VSCFOA-GRNN進行訓練時只可采用同一λj為調度規則的數據.

2.2? ?實時VSCFOA-GRNN神經網絡調度決策

在離線階段通過仿真構建知識庫和訓練VSCFOA-GRNN神經網絡后，可進入實時階段進行裝配線的物料搬運調度.

在每個調度決策點tk時刻，調度目標權重或裝配系統的產品配比發生改變，觸發物料搬運系統進行決策，假設此時的產品配比為mk，調度目標權重ωk =（ωM，ωD），那么調度系統可以通過VSCFOA-GRNN神經網絡找到與mk最相似的產品配比st（mk）∈mall. 檢索知識庫得到不同的調度規則在產品配比為st（mk）條件下得到的裝配線產量和多載量小車的物料搬運距離，根據式（1）得到目標函數值，選擇令目標函數值最大的調度規則λk，即：

3? ?算法性能仿真分析

3.1? ?仿真案例參數

參照文獻[2]和文獻[15]中的相關參數，ωM和ωD的取值分別服從區間[2，4]和[-0.004 5，-0.001 8]內的均勻分布. 產品配比的取值空間離散化為 66 個點，每類產品的生產比例間隔為0.1，即第一類產品的生產比例為ρ1 = 0，0.1，0.2，…，1;第二類產品的生產比例為ρ2 = 0，0.1，0.2，…，1 - ρ1;第三類產品的生產比例為ρ3 = 0，0.1，0.2，…，1 - ρ1 - ρ2. 設定仿真的實驗時間為72 h，包含8 h的預熱時間. 對各組產品配比和調度規則分別進行5次實驗.

3.2? ?備選調度規則之間的對比

為了進一步說明當產品配比發生改變時，不同的調度規則會對調度性能產生極大的影響，在比較VSCFOA-GRNN神經網絡和其他調度方法的性能之前，先對備選調度規則的調度性能進行分析比較. 將66個產品配比每隔兩點取出一個，形成22組產品配比，其使用各備選調度規則時的裝配線產量和物料搬運距離如圖4所示.

3.4? ?對比VSCFOA-GRNN神經網絡與其他神經

網絡

神經網絡方法可以用來預測不同調度方法的性能，并依此進行調度方法的選擇. 為了驗證VSCFOA-GRNN方法對不同調度規則性能預測的準確性，利用仿真實驗對比VSCFOA-GRNN和基于果蠅優化算法優化的廣義回歸神經網絡（FOA-GRNN）、標準的廣義回歸神經網絡（GRNN）與基礎神經網絡徑向基神經網絡（RBF），如表3所示. 改變決策點的個數，即通過增加產品配比和調度目標權重的組數來擴大問題規模，每兩個決策點之間的調度期間時長為72 h，每個決策點中的各個神經網絡進行10次實驗，目標函數取平均值.

對神經網絡在不同決策點的平均目標函數值進行對比，通過各神經網絡與VSCFOA-GRNN的百分比偏差（PD）來比較其有效性. 由表3可知，VSCFOA-GRNN的預測準確性明顯優于其他3種對比網絡. 隨著問題規模擴大，決策點個數增加，mk和ωk發生變化，此時調度系統利用神經網絡在知識庫中選取st（mk）. 由于預測偏差導致的st（mk）與實際選取的產品配比mk存在一定誤差，理論最優目標函數值與實際目標值則存在偏差，且隨著問題規模的擴大，累積偏差值逐漸增大. 由于各神經網絡預測性能不同，其對應目標函數值之間的PD隨著問題規模的擴大而不斷增加. 由此說明，隨著問題規模的擴大，VSCFOA-GRNN神經網絡的預測優越性愈發明顯.

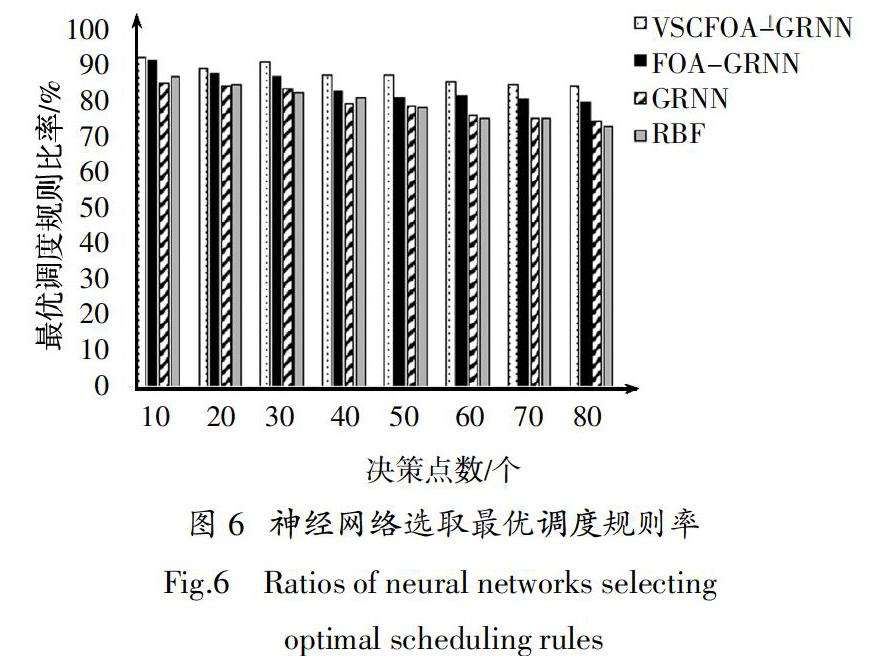
本案例仿真數據為美國通用汽車公司S區部分汽車裝配線的真實數據[15]，本節中大規模問題的決策點范圍即針對實際生產管理設置. 由圖6可知，在實際問題規模中，VSCFOA-GRNN在最優調度規則選取率上呈現出明顯的平穩性與高效性. 其在尋優率方面遠超其他3種對比神經網絡，百分比偏差自衍生的小問題規模向實際問題規模逐步增大，最大差距達19.18%. 同時，VSCFOA-GRNN在最優調度規則選擇比率上持平85%以上，下降趨勢呈平緩狀態，其在實際問題規模中的實用性達標. 通過以上橫縱兩向對比，VSCFOA-GRNN在解決實際生產中多載量小車動態調度決策問題的有效性得以驗證.

4? ?結? ?論

本文以多載量小車為主要研究對象，考慮調度目標權重和產品配比可變環境下的動態調度問題，即當產品配比和調度目標權重發生變化時，對多載量小車采取何種調度規則進行決策. 以產量和物料搬運距離作為衡量指標建立目標函數，通過調度性能指標（裝配線產量和搬運距離）與產品配比和調度規則之間的關系，利用神經網絡尋找與給定產品配比最相似且存儲于知識庫中的產品配比，利用知識庫中的數據進行最優調度規則的選取. 經過實驗驗證，本文提出的動態調度方法準確率高，調度效果好，對本文的動態環境具有較好的適應能力. 但是，本文僅著眼于單個物流區域中多載量小車的動態調度問題，今后將對多個物流區域相互關聯的調度問題進行探討，并分析和改善其相互作用情況.

參考文獻

[1]? ? CHANG Q，PAN C Y，XIAO G X，et al. Integrated modeling of automotive assembly line with material handling [J]. Journal of Manufacturing Science and Engineering，2013，135（1）：011018.

[2]? ? 周炳海，徐佳惠.基于支持向量機的多載量小車實時調度[J].吉林大學學報（工學版），2016，46（6）：2027—2033.

ZHOU B H，XU J H. SVM-based real-time scheduling approach of multi-load carriers [J]. Journal of Jilin University （Engineering and Technology Edition），2016，46（6）：2027—2033. （In Chinese）

[3]? ? EMDE S，ABEDINNIA H，GLOCK C H. Scheduling electric vehicles making milk-runs for just-in-time delivery [J]. IISE Transactions，2018，50（11）：1013—1025.

[4]? ? FATHI M，ALVAREZA M J，RODR?GUEZB V，et al. A multiobjective optimization algorithm to solve the part feeding problem in mixed-model assembly lines [J]. Mathematical Problems in Engineering，2014，11（1）：809—812.

[5]? ? FATHI M，RODR?GUEZ V，ALVAREZ M J. A novel memetic ant colony optimization-based heuristic algorithm for solving the assembly line part feeding problem [J]. International Journal of Advanced Manufacturing Technology，2014，75（1）：629—643.

[6]? ? FATHI M，RODR?GUEZ V，FONTES D B M M，et al. A modified particle swarm optimisation algorithm to solve the part feeding problem at assembly lines [J]. International Journal of Production Research，2015，54（3）：878—893.

[7]? ? SHIUE Y R，LEE K C，SU C T. Real-time scheduling for a smart factory using a reinforcement learning approach [J]. Computers & Industrial Engineering，2018，125：604—614.

[8]? ? SEKER A，EROL S，BOTSALI R. A neuro-fuzzy model for a new hybrid integrated process planning and scheduling system [J]. Expert Systems with Applications，2013，40（13）：5341—5345.

[9]? ? FAGAN D，FENTON M，LYNCH D，et al. Deep learning through evolution：a hybrid approach to scheduling in a dynamic environment[C]// International Joint Conference on Neural Networks. Anchorage，Alaska：Institute of Electrical and Electronics Engineers，2017：775—782.

[10]? ZANG Z L，WANG W L，SONG Y H，et al. Hybrid deep neural network scheduler for job-shop problem based on convolution two-dimensional transformation [J]. Computational Intelligence and Neuroscience，2019，2019（2）：1—19.

[11]? SONG Y，SHI G，CHEN L Y，et al. Remaining useful life prediction of turbofan engine using hybrid model based on autoencoder and bidirectional long short-term memory [J]. Journal of Shanghai Jiaotong University （Science），2018，23（S1）：85—94.

[12]? ZHUO P C，ZHU Y，WU W X，et al. Real-time fault diagnosis for gas turbine blade based on output-hidden feedback elman neural network [J]. Journal of Shanghai Jiaotong University （Science），2018，23（S1）：95—102.

[13]? WANG L，SHI Y L，LIU S. An improved fruit fly optimization algorithm and its application to joint replenishment problems [J]. Expert Systems with Applications，2015，42（9）：4310—4323.

[14]? SPECHT D F. A general regression neural network [J]. IEEE Transactions on Neural Networks，1991，2（6）：568—576.

[15] CHEN C，XI L F，ZHOU B H，et al. A multiple-criteria real-time scheduling approach for multiple-load carriers subject to LIFO loading constraints [J]. International Journal of Production Research，2011，49（16）：4787—4806.