多段填充復合蜂窩結構的動態響應特性研究

張新春 沈振峰 吳鶴翔 白江畔 曹應平

摘? ?要：基于多胞材料獨特的力學性能和微結構可設計性強的優勢，提出一種多段三角形和六角形蜂窩填充能量吸收復合結構模型. 利用顯式動力有限元方法對該模型的動力響應特性和比吸能進行研究，重點討論了不同恒定沖擊速度下，蜂窩結構的排布及其相對密度對復合蜂窩結構宏觀變形、動態平臺應力、沖擊載荷一致性和能量吸收能力的影響. 研究結果表明，所設計的多段填充復合蜂窩結構能夠讓軸力和彎曲變形共同參與整體變形，實現I類和II類能量吸收結構的優勢互補. 通過對各段內微結構及段長的合理選擇，復合蜂窩結構的沖擊載荷效率明顯提高，沖擊應力波動幅度明顯降低，能夠有效地提高并控制蜂窩結構能量吸收效率. 本文對完善多胞結構的耐撞性設計方法和控制能量吸收過程具有指導意義.

關鍵詞：固體力學;蜂窩材料;沖擊載荷一致性;能量吸收;有限元分析

中圖分類號：O347? ? ? ? ? ? ? ? ? ? ? ? ? ? 文獻標志碼：A

Abstract：Based on the potential advantages of unique mechanical performance and the micro-structure better design ability for cellular materials，this paper proposes a multi-segment energy absorption composite model filled with triangular and hexagonal honeycomb. Then， the dynamic response characteristic and the specific energy absorption of this model are numerically investigated by using explicit dynamic finite element （EDFE） method. The effects of honeycomb structure arrangement and relative density on the deformation mode， dynamic plateau stress， crushing load uniformity， and energy absorption capacity of the composite honeycombs are discussed in detail under different constant impact velocities. Research results show that the multi-segment filled honeycombs can realize the complementary advantages of type I and type II structures， which enables the axial force and bending deformation to participate in the overall deformation. Through the proper choice of cell micro-structures in each segment and the segment length， the crushing load efficiency of composite honeycomb is obviously improved and the fluctuation range of impact stress is significantly reduced. Composite honeycomb can effectively improve and control its energy absorption efficiency. These results are useful for the crashworthiness design and energy absorption controllable properties of cellular materials.

Key words：solid mechanics;honeycombs;crushing load uniformity;energy absorption;finite element （FE） analysis

隨著材料制備工藝和機械加工業的快速發展，多孔材料及其夾芯結構在高速列車、超高速飛行器、裝甲車和艦船等高能耗裝備中得到廣泛應用，并引起國內外學者的廣泛關注[1-2]. 與其他材料不同，蜂窩材料具有千變萬化的微結構和高孔隙率，使之具有獨特的力學性能和可設計性強等優勢，能夠在保持較低的應力水平下吸收大量的沖擊動能，被廣泛應用于各種沖擊防護構件中. 這對蜂窩材料的耐撞性設計提出了更高的要求，如沖擊峰值應力的抑制、沖擊應力增強的控制和能量吸收率的提高等. 因此，如何提高并有效控制材料的能量吸收效率是蜂窩材料及其結構耐撞性設計的關鍵問題之一.

事實上，在沖擊載荷下，蜂窩材料的胞壁可能分別承受軸力、彎矩或剪力作用. 根據沖擊變形機制的不同，蜂窩材料[3]可分為彎曲主導型結構（六角形、圓形、菱形或正方形結構等）和拉伸主導型結構（三角形、Kagome結構或混合型結構等）. 前者稱之為第Ⅰ類能量吸收結構，后者稱之為第Ⅱ類能量吸收結構. 目前，關于這兩類結構的沖擊響應特性和能量吸收方面的研究已經展開. Ruan等[4]討論了相對密度和沖擊速度對六角形蜂窩結構面內變形模式和平臺應力的影響;Liu和Zhang等[5-6]討論了微結構及密度梯度對蜂窩材料動態響應特性和能量吸收能力的影響;Qiu等[7]綜合分析了一些平面蜂窩結構的沖擊動力學響應特性，指出拉伸主導型結構的平臺應力要高于彎曲主導型;Chen等[8]研究了密度梯度對三角形和六邊形網格薄壁圓管結構峰值載荷和能量吸收能力的影響;Zhang等[9-10]討論了胞元微結構對負泊松比蜂窩結構面內動力響應特性的影響，給出了拉脹蜂窩結構的平臺應力經驗公式; Boldrin等[11] 研究了六角形填充梯度復合蜂窩結構的動態響應特性;白中浩等[12]討論了不同截面形狀和結構參數對正八邊形多胞薄壁管吸能特性的影響. 研究結果表明[5-7]，在相同的相對密度下，第Ⅱ類能量吸收結構（即拉伸主導型結構）具有較高的塑性坍塌強度，在一定程度上強化了結構，提高了沖擊能量吸收能力，但在能量吸收方面表現出不受歡迎的高的沖擊峰值應力;而第Ⅰ類能量吸收結構（即彎曲主導型結構）卻能調動試件發生整體變形，表現為一條相對"平坦"的曲線. 可見，以上兩類結構在作為能量吸收構件單獨使用時均不理想，如果設計一種能量吸收結構，讓軸力/膜力也參與整體變形，則將比單純利用彎曲塑性變形所吸收沖擊能量的效率要高.

基于復合材料的概念，通過改變不同填充段胞元微結構，將不同類型的能量吸收結構相互耦合，本文提出了一種多段填充復合蜂窩結構模型. 采用非線性動力有限元方法，研究了不同恒定沖擊速度下各段結構排布和相對密度對復合蜂窩材料宏觀變形模式、動態平臺應力、沖擊載荷一致性和能量吸收效率的影響.

1? ?計算模型

1.1? ?有限元模型

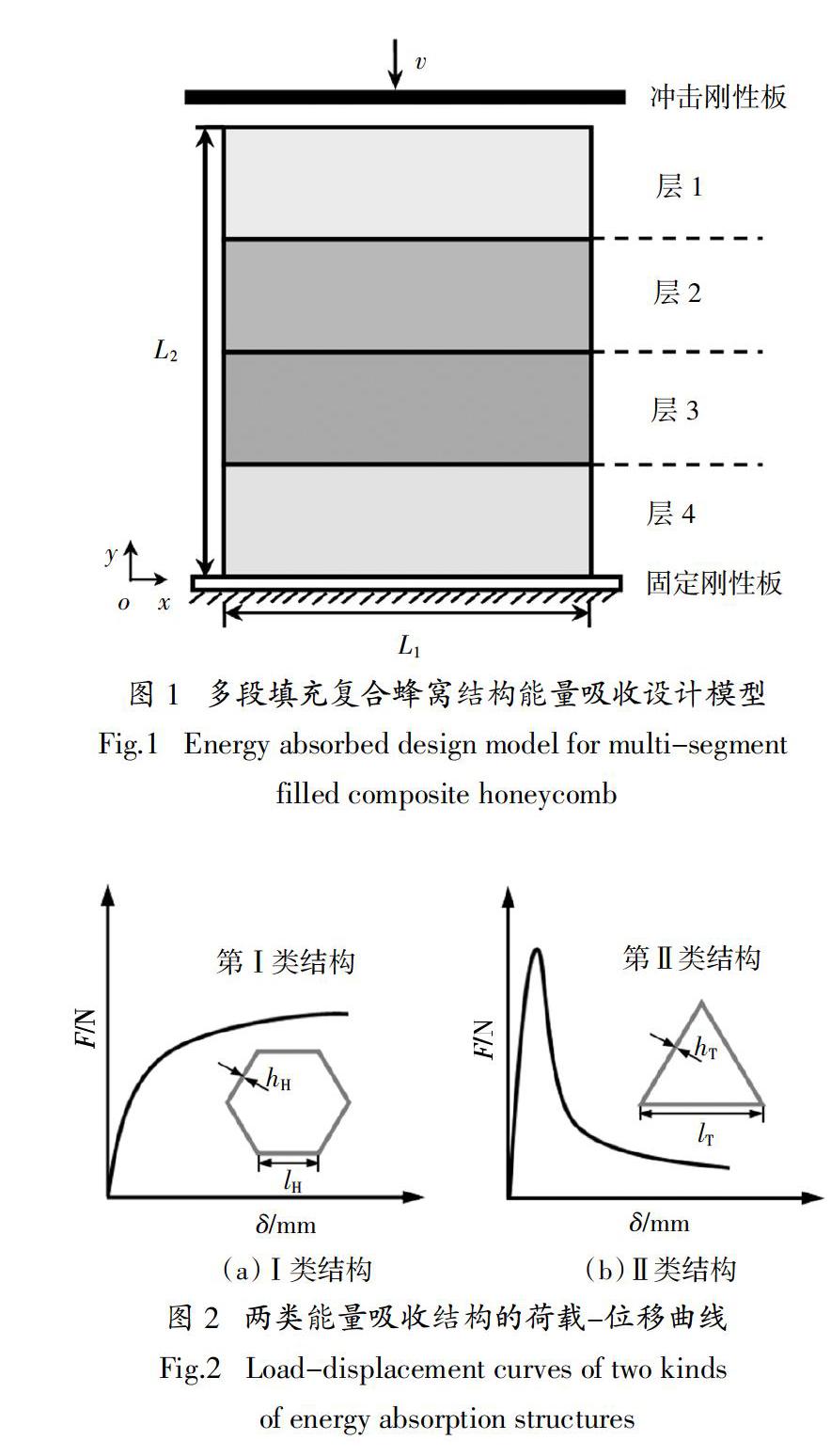
多段填充復合蜂窩結構的能量吸收設計模型如圖1所示. 計算模型由4段胞元層構成，每段分別由第Ⅰ類能量吸收結構（六角形胞元）或第Ⅱ類能量吸收結構（三角形胞元）所填充. 兩類能量吸收結構的典型荷載-位移曲線如圖2所示，填充過程中保證蜂窩材料的相對密度和胞壁長度不變. 試件沿x和y方向的尺寸分別為L1 = 54 mm，L2 = 74.8 mm，模型的面外厚度為單位厚度. 利用顯式動力有限元方法并借助ABAQUS/EXPLICIT進行沖擊動力學特性模擬，胞壁采用S4R殼單元（4節點，縮減積分單元）進行離散. 為了保證收斂和計算精度，沿厚度方向取5個積分點.

圖3為多段填充復合蜂窩結構設計示意圖. 針對某一特定的結構排布（如試件HHTT，H表示六角形結構;T表示三角形結構），試件HHTT表示六角形結構靠近沖擊端，三角形結構靠近固定端. 基體材料為金屬鋁，并假定為理想彈塑性模型，服從Mises屈服準則. 主要材料參數為[10]：楊氏模量Es=69 GPa，屈服應力σys = 76 MPa，密度ρs = 2 700 kg/m3，泊松比μ = 0.3，取強化模量為零. 對于計算中可能的接觸，將剛性板與試件間定義為面-面自動接觸，摩擦系數為0.02[10];試件內部各胞元間定義為通用接觸，且無摩擦. 采用與文獻[3-7]相同的邊界條件，即蜂窩試件置于底端固定剛性板上，試件左右兩側自由. 為保證變形的平面應變狀態，在計算過程中，約束所有節點沿面外方向的位移以防止面外屈曲的發生. 另外，本文在大變形沖擊過程中不考慮材料損傷對多段填充復合蜂窩結構動態響應特性和能量吸收能力的影響.

1.2? ?相對密度

相對密度是描述多胞材料及結構力學性能的一個重要指標，其權重超出了其他影響參數. 對于規則三角形蜂窩，相對密度為[1]：

1.3? ?模型可靠性分析

為驗證有限元模型的可靠性，基于文獻[4]，圖4給出了正六角形蜂窩在沖擊速度v=7 m/s時的變形模式. 在基體材料、邊界條件和沖擊速度完全相同的條件下，計算結果與文獻[4]吻合較好，證明了有限元模型的可靠性. 另外，有限元模型的可靠性還依賴于網格尺寸的大小. 網格尺寸對六角形蜂窩平臺應力和計算時間的影響如圖5所示. 由圖5可知，當網格尺寸為0.35 mm時，模型的平臺應力趨近于穩定，計算時間較短. 考慮到計算效率和計算結果的精確性，本文模型的網格尺寸選用0.35 mm.

2? ?計算結果與討論

2.1? ?變形模式

對于Ⅰ類和Ⅱ類能量吸收結構，大量學者已對其沖擊變形模式進行了研究[4-7，13]. 研究結果表明，胞元微結構和沖擊速度是影響蜂窩材料變形模式的重要因素. 然而，與Ⅰ類和Ⅱ類蜂窩結構不同，多段填充復合蜂窩結構由不同微拓撲結構蜂窩胞元層組成，沖擊過程中可以實現I類和II類能量吸收結構的優勢互補. 在沖擊荷載作用下，復合蜂窩結構的變形模式更加復雜.

圖6給出了不同沖擊速度下兩種復合蜂窩結構（HTHT和THTH）在名義應變ε = 0.32時的宏觀變形模式. 低速沖擊載荷下（v = 3 m/s），與規則填充蜂窩不同，試件沒有發生明顯整體變形. 復合蜂窩結構的六角形填充蜂窩層首先發生局部變形，出現“X”型變形帶，如圖6（a）所示. 這是因為在低速沖擊下，塑性坍塌強度對蜂窩材料變形模式的影響起主導地位. 六角形蜂窩填充層的塑性坍塌強度較低，三角形蜂窩填充層的塑性坍塌強度較高;隨著沖擊速度的增加（v = 20 m/s），慣性效應相對增強，結構排布對破壞的引導作用減弱. 塑性坍塌強度和沖擊速度同時影響復合蜂窩結構的變形模式，試件局部變形總是從沖擊端開始形成，如圖6（b）所示. 隨著壓縮位移的增加，兩種復合蜂窩的變形模式差異明顯. 靠近沖擊端為六角形結構的復合蜂窩（HTHT）的變形主要集中在首層塑性坍塌強度較低的六角形結構，而反向布置的復合蜂窩（THTH）的變形出現在首層結構的同時也蔓延至塑性坍塌強度較低的六角形結構處，三角形蜂窩和六角形蜂窩結構相互耦合，試件發生整體變形;隨著沖擊速度的進一步提高（v = 120 m/s），慣性效應占主導地位，不同復合蜂窩結構的變形模式趨于類似，從沖擊端到固定端發生逐層壓潰變形模式，呈現出“I”形的變形帶，如圖6（c）所示.

綜上所述，在低速沖擊下，塑性坍塌強度對變形模式的影響占主導地位，結構排布對破壞的發生具有一定的引導作用，復合蜂窩結構中塑性坍塌強度低的填充層首先發生局部變形;在高速沖擊下，慣性效應占主導地位;在中速沖擊下，試件的變形將受到沖擊速度和塑性坍塌強度的影響，變形模式與蜂窩材料層的排布方式有關. 因此，復合蜂窩材料面內沖擊變形模式主要依賴于蜂窩材料的塑性坍塌強度，各段填充層排布方式和沖擊速度.

2.2? ?平臺應力

平臺應力和密實應變是描述多胞材料動態吸能特性的重要指標. 平臺應力σp為：

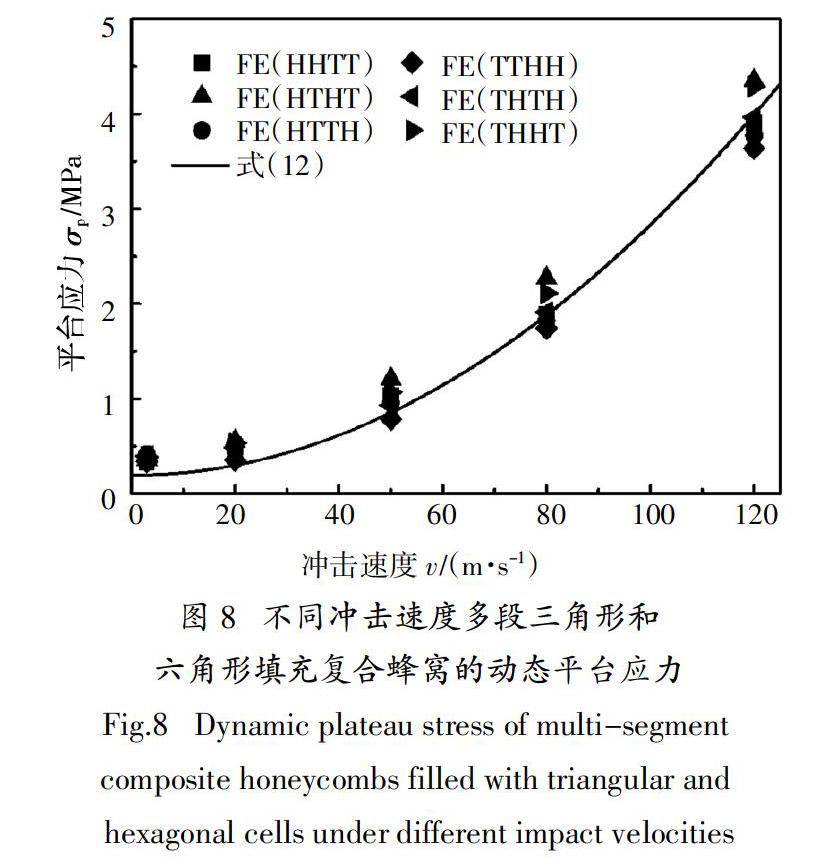
以HTHT復合蜂窩結構為例，圖9給出了不同沖擊速度下相對密度對多段填充復合蜂窩試件動態平臺應力影響. 圖9中顯見，對于相同的相對密度，多段填充復合蜂窩結構的平臺應力隨沖擊速度的增大而增大，與沖擊速度的平方幾乎成正比. 在同一沖擊速度下，相對密度越大，復合蜂窩結構的平臺應力越大.

2.3? ?沖擊載荷一致性

能量吸收結構應當在能量耗散的過程中保持良好的載荷一致性，這就要求其反作用力的峰值應低于引起損傷的臨界值，避免引起被保護構件的破壞. 同時，蜂窩材料的反作用力應盡可能維持恒定. 評價蜂窩材料載荷一致性[3]的兩個指標分別為沖擊載荷效率CLE和平均應力波動幅度Δσ，分別為：

圖10給出了不同沖擊速度下兩類典型蜂窩結構的沖擊載荷一致性比較. 在相同相對密度下，當沖擊速度大于20 m/s時，三角形蜂窩的沖擊載荷效率高于六角形蜂窩材料（圖10（a）），因為在相同沖擊速度下拉伸主導型結構的平臺應力要高于彎曲主導型結構[5]. 不同沖擊速度下三角形蜂窩的應力波動幅度大于六角形蜂窩，且隨沖擊速度的增大波動幅度變化越大（圖10（b）），這充分體現拉伸主導型結構具有較強的波動性，不適宜作為理想能量吸收結構.

在給定沖擊速度下（v = 20 m/s），圖11給出了相對密度對三角形和六角形蜂窩的沖擊載荷效率和平均應力波動幅度的影響. 從圖11中可以看出，兩類典型蜂窩結構的沖擊載荷效率和平均應力波動幅度隨相對密度的增加有增大的趨勢，并且三角形蜂窩的沖擊載荷效率和平均應力波動幅度要大于六角形蜂窩.

圖12給出了多段填充復合蜂窩結構在不同沖擊速度下的沖擊載荷效率比較. 作為對比，圖中還給出了相同相對密度下兩類規則蜂窩材料（三角形和六角形）的計算結果比較. 在低速沖擊載荷下（v = 3 m/s），胞元結構排布是影響復合蜂窩材料沖擊載荷效率的主要因素. 復合蜂窩材料的變形首先集中在塑性坍塌強度較低的六角形填充結構段處，試件的最大峰值應力降低. 隨著壓縮位移的增加，變形向塑性坍塌強度較高的三角形填充結構擴展，引起平臺

應力的逐步提高. 由于彎曲主導型結構和拉伸主導型結構的耦合，多段復合蜂窩材料（除TTHH）的沖擊載荷效率明顯高于普通三角形和六角形蜂窩;隨著沖擊速度的增加（v = 20 m/s），多段復合蜂窩材料（除TTHH）的沖擊載荷效率仍高于普通蜂窩材料. 但與低速沖擊相比，沖擊載荷效率將降低，如圖12（b）所示. 慣性效應增強對頂端填充層的影響作用變大，靠近沖擊端為六角形的復合蜂窩（HHTT、HTHT、HTTH）的沖擊載荷效率略高于靠近沖擊端為三角形的試件（TTHH、THTH、THHT）. 可見，將塑性坍塌強度低的蜂窩結構置于沖擊端處，可提高蜂窩材料的沖擊載荷效率;隨著沖擊速度的進一步提高（v = 120 m/s），慣性效應增強，在高速沖擊下試件的沖擊應力上下振蕩明顯，多段復合蜂窩材料的沖擊載荷效率介于三角形和六角形蜂窩結構之間，如圖12（c）所示.

圖13給出了多段填充復合蜂窩材料在不同沖擊速度下的平均應力波動幅度比較. 從圖中可以看出，在不同沖擊速度下，復合蜂窩材料的平均應力波動幅度基本位于三角形和六角形蜂窩之間. 可見，由于彎曲主導型結構的引入，多段填充復合蜂窩材料的平均應力波動幅度明顯降低. 隨著沖擊速度的增加，復合蜂窩材料的平均應力波動幅度相應增大.

2.4? ?能量吸收特性

對于多胞材料與結構，通常采用單位質量的能量吸收Em來評估吸能特性，可表示為：

圖14給出了多段填充復合蜂窩材料（HTHT、THTH）在不同沖擊速度下的單位質量能量吸收情況. 作為對比，圖中還給出了三角形和六角形蜂窩材料比能量吸收特性. 由圖14可知，多段填充復合蜂窩材料的單位質量能量吸收能力介于六角形蜂窩和三角形蜂窩之間. 在低速沖擊下（v=3 m/s），微結構排布將主導宏觀結構變形，兩種復合蜂窩材料的比能量吸收差別不大，在沖擊的初始階段與六角形蜂窩的吸能效果一致，隨著壓縮的進一步增加，比能量吸收曲線逐漸靠近三角形蜂窩（圖14（a））;隨著沖擊速度的增加（v=20 m/s），塑性坍塌強度和沖擊速度同時影響復合蜂窩材料宏觀變形，不同排布復合蜂窩的比能量吸收有了明顯的差異（圖14（b））. 在初始沖擊階段，試件HTHT的比能量吸收接近于六角形蜂窩，而試件THTH的比能量吸收接近于三角形蜂窩，這與復合蜂窩材料的變形規律基本吻合;在高速沖擊載荷（v=120 m/s），慣性效應增強，微結構排布的影響減弱，多段填充復合蜂窩材料的比能量吸收趨近于六角形蜂窩和三角形蜂窩（圖14（c））. 可見，在高速沖擊載荷下，多段填充復合蜂窩材料的比能量吸收主要取決于沖擊速度和相對密度.

3? ?結? ?論

基于復合材料的概念，通過彎曲主導型和拉伸主導型結構兩類能量吸收結構的相互耦合，本文提出了一種多段填充復合蜂窩材料模型. 利用顯式非線性動力有限元方法，對多段填充復合蜂窩結構動態響應特性和沖擊載荷一致性進行了研究. 得出如下結論：

1）多段填充復合蜂窩材料的變形模式主要依賴于各段填充層塑性坍塌強度和沖擊速度. 在低速沖擊下，多段填充復合蜂窩材料的沖擊變形模式取決于各段填充層的塑性坍塌強度;在中速沖擊下，多段填充復合蜂窩材料的宏觀變形與各段的塑性坍塌強度和沖擊速度有關;在高速沖擊下，慣性效應將主導多段填充復合蜂窩材料的變形模式.

2）所設計的多段填充復合蜂窩材料能夠實現拉伸主導型結構和彎曲主導型結構的優勢互補. 復合蜂窩材料具有良好的沖擊載荷一致性，在中低速沖擊載荷下，復合蜂窩材料的沖擊載荷效率要高于三角形和六角形蜂窩. 由于彎曲主導型結構的引入，多段填充復合蜂窩材料的平均應力波動幅度明顯降低.

3）基于一維沖擊波理論，給出了多段填充復合蜂窩材料平臺應力經驗公式，理論計算結果與數值模擬結果吻合較好. 此外，通過對各段內微結構及段長的合理選擇，能夠有效地提高并控制蜂窩材料能量吸收效率，達到控制蜂窩材料能量吸收能力的目的.

參考文獻

[1]? ?GIBSON L J，ASHBY M F. Cellular solids：structure and properties [M]. Cambridge：Cambridge University Press，1997：5—35.

[2]? ?SUN Y L，LI Q M. Dynamic compressive behaviour of cellular materials：a review of phenomenon，mechanism and modeling [J]. International Journal of Impact Engineering，2018，112：74—115.

[3]? ?WU H X，LIU Y，ZHANG X C. In-plane crushing behavior and energy absorption design of composite honeycombs[J]. Acta Mechanica Sinica，2018，34：1108—1123.

[4]? ? RUAN D，LU G，WANG B，et al. In-plane dynamic crushing of honeycombs-a finite element study [J]. International Journal of Impact Engineering，2003，28（2）：161—182.

[5]? ? LIU Y，ZHANG X C. The influence of cell micro topology on the in-plane dynamic crushing of honeycombs [J]. International Journal of Impact Engineering，2009，36（1）：98—109.

[6]? ?ZHANG X C，AN L Q，DING H M. Dynamic crushing behavior and energy absorption of honeycombs with density gradient [J]. Journal of Sandwich Structures and Materials，2014，16（2）：125—147.

[7]? ?QIU X M，ZHANG J，YU T X. Collapse of periodic planar lattices under uniaxial compression，part II：dynamic crushing based on finite element simulation [J]. International Journal of Impact Engineering，2009，36：1231—1241.

[8]? ?CHEN L M，ZHANG J，DU B，et al. Dynamic crushing behavior and energy absorption of graded lattice cylindrical structure under axial impact load [J]. Thin-Walled Structures，2018，127：333—343.

[9]? ?ZHANG X C，AN L Q，DING H M，et al. Influence of cell micro structure on the in-plane dynamic crushing of honeycombs with negative Poissons ratio [J]. Journal of Sandwich Structures and Materials，2015，17（1）：26—55.

[10]? 韓會龍，張新春，王鵬. 負泊松比蜂窩材料的動力學響應及能量吸收特性[J]. 爆炸與沖擊，2019，39（1）：013103.HAN H L，ZHANG X C，WANG P. Dynamic responses and energy absorption properties of honeycombs with negative Poissons ratio [J]. Explosion and Shock Waves， 2019， 39（1）： 013103. （In Chinese）

[11]? BOLDRIN L，HUMMEL S，SCARPA F，et al. Dynamic behaviour of auxetic gradient composite hexagonal honeycombs [J]. Composite Structures，2016，149：114—124.

[12]? 白中浩，王飛虎，郭厚銳. 正八邊形多胞薄壁管吸能特性仿真和優化[J]. 湖南大學學報（自然科學版），2015，42（10）：16—22.BAI Z H，WANG F H，GUO H R. Simulation and optimization of octagon multi-cell thin-walled tubes for energy absorption character [J]. Journal of Hunan University（Natural Sciences），2015，42（10）：16—22. （In Chinese）

[13]? WANG H，LU Z X，YANG Z Y，et al. In-plane dynamic crushing behaviors of a novel auxetic honeycomb with two plateau stress regions [J]. International Journal of Mechanical Sciences，2019，151：746—759.

[14] REID S R，PENG C. Dynamic uniaxial crushing of wood [J]. International Journal of Impact Engineering，1997，19（5/6）：531—570.