起伏振動下傾斜管內單相流流動阻力特性分析

周云龍，劉起超，汪俊超

(東北電力大學 能源與動力工程學院，吉林省 吉林市 132012)

21世紀以來，環境問題和能源危機一直是制約社會發展的“緊箍咒”，核能具有高效、穩定和可控的優點，被各大國家所青睞。2010年9月，俄羅斯第1座浮動核電站下水。2016年11月，我國首座海上核電站開工，并計劃在南海建設20座。海上核電站在運行過程中必然受到海浪的影響而處于起伏振動狀態，此時核電站一回路的冷卻液流動也處于起伏振動狀態，一旦錯誤估計一回路的冷卻液流動阻力，會影響反應堆的冷卻效果，造成嚴重的安全事故。因此，正確分析和計算起伏振動狀態下單相水的流動阻力，對海上核電站的安全運行至關重要。

目前關于穩定狀態下單相流動的阻力計算方法的研究已非常成熟，尼古拉斯公式和莫迪圖均能用于單相流動阻力的計算[1]。非穩定狀態下單相流動阻力的研究相對還較少，高璞珍等[2]對海洋條件下的核動力裝置一回路冷卻劑的流動進行建模，分析了冷卻劑的受力情況，得出了非穩定狀態下流動附加壓降的計算公式，為非穩態流動阻力特性的研究奠定了理論基礎。Yan等[3-4]對流動進行簡化，建立了搖擺狀態下單相水流動特性的理論模型。張金紅等[5]對搖擺狀態下內徑34.5 mm的有機玻璃管內單相水的摩擦壓降特性進行了實驗研究，應用能量方程和Darcy公式求解摩擦系數，進而擬合出用于計算搖擺狀態下單相水的摩擦阻力系數的計算公式。欒鋒等[6]通過實驗研究了不同管徑水平管單相水的阻力特性，發現搖擺狀態下單相水摩擦壓降也呈現周期性波動，波動周期與搖擺周期一致，并分析了搖擺周期、搖擺幅度、雷諾數和管徑對摩擦系數的影響，給出了搖擺狀態下單相水摩擦系數的計算公式。幸奠川等[7-12]對搖擺狀態下單相強制循環層流阻力特性、湍流阻力特性和矩形窄通道單相流摩擦阻力進行了實驗研究，得出了搖擺狀態層流瞬時摩擦阻力系數的計算公式及摩擦系數隨振動參數的變化規律。譚思超等[13]對搖擺運動下窄矩形通道低流速單相瞬變流動時均阻力特性進行了實驗研究，發現先求解阻力系數和先求解壓差再求解阻力系數的結果不同，分別能夠代表時均黏性耗散和時均摩擦阻力壓降。Yu等[14]研究了振動對自然循環流動特性的影響，提出了能準確預測單相自然循環流動流量波動特性的模型。謝清清等[15]在不同搖擺周期和角度下對光滑窄矩形通道內單相流動阻力特性進行了實驗研究，發現摩擦阻力系數具有周期性波動特性，摩擦阻力系數與雷諾數呈反比，與搖擺角加速度呈正比。

目前非穩態流動阻力的研究主要集中在搖擺運動方面，尚未有關于起伏振動單相流動阻力的相關研究。本文通過對不同流動和振動工況下單相水的流動阻力特性進行分析，將傳統摩擦壓降和振動引起的附加壓降定義為起伏振動下的摩擦壓降，得出起伏振動狀態下單相水的流動阻力變化規律，為起伏振動下單相流動阻力的計算提供指導。

1 實驗裝置和方法

本文實驗采用電磁式起伏振動臺，在控制器的作用下產生指定類型的起伏振動。實驗系統如圖1所示。

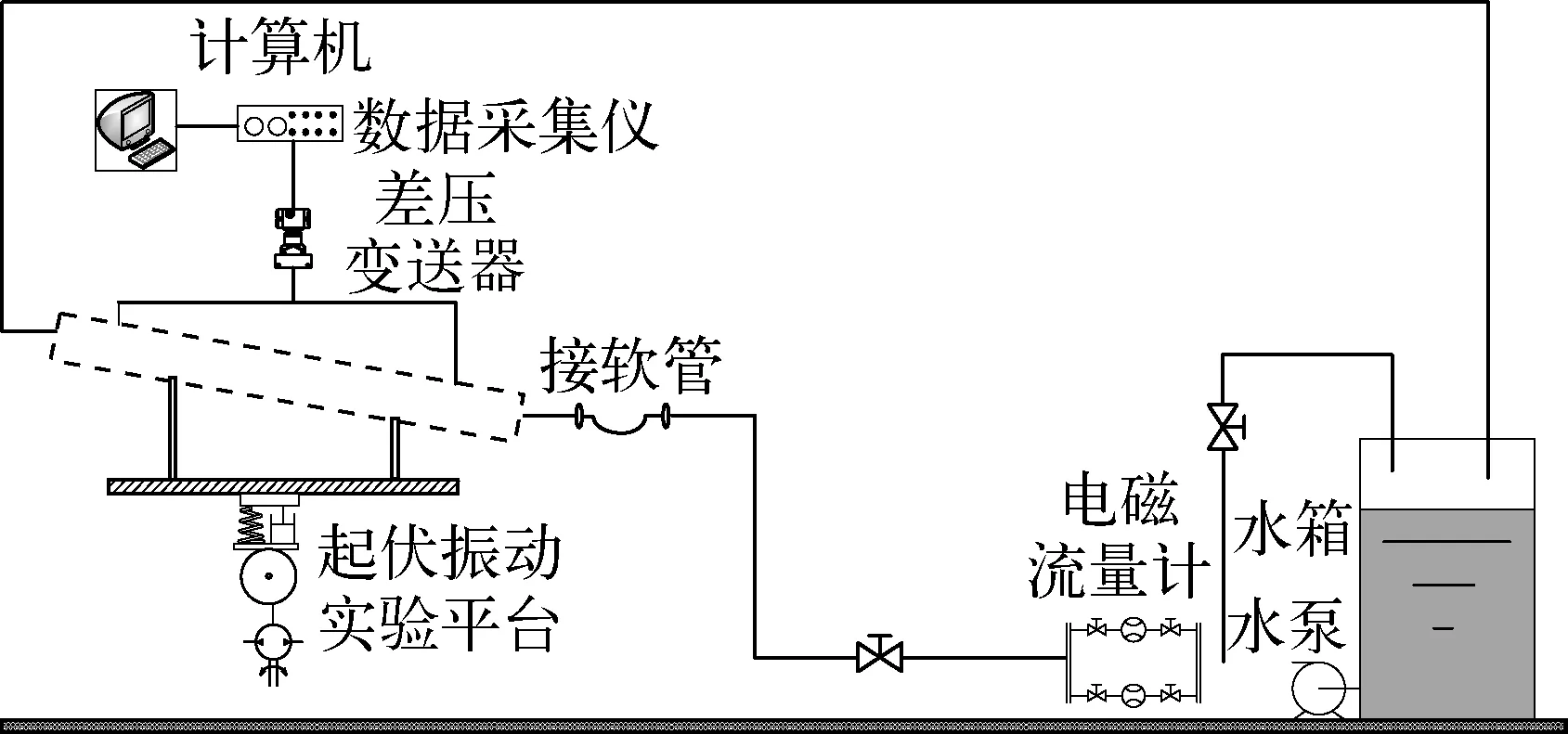
圖1 實驗系統Fig.1 Experimental system

振動臺在控制器的控制下做正弦起伏振動，其運動規律為：

y=Asin(2πft)

(1)

v=2πfAcos(2πft)

(2)

a=-4π2f2Asin(2πft)

(3)

式中：y為瞬時位移，m；A為振幅，m；f為振動頻率，Hz；t為時間，s；v為瞬時振動速度，m/s；a為瞬時振動加速度，m/s2。

實驗段為光滑有機玻璃圓管，管道內徑分別為15、20和30 mm，通過支架固定在振動臺上，實驗段傾角θ分別為10°、24°和45°。實驗段上開有兩個測壓孔，間隔為0.8 m，用于流動壓力的取樣。流動壓降采用差壓傳感器測量，量程為0～25 kPa，精度為0.2級。振動臺的加速度用加速度傳感器進行測量，量程為0～30 m/s2，精度為0.5級。管道流量采用電磁流量計測量，量程為0～10 m3/h，精度0.5級。振動參數分別為：頻率2、5和8 Hz，振幅2、5和10 mm。

2 實驗數據處理

文獻[2]指出，海洋條件下流動受到附加力的作用會產生附加壓降，因此起伏振動傾斜管單相水的壓降主要由摩擦壓降Δpf、重位壓降Δpg和附加壓降Δpadd組成，即：

Δp=Δpf+Δpg+Δpadd

(4)

對于傾斜管，兩個引壓管之間存在液柱差，該部分壓力差值與實驗段中水的重位壓降相互抵消。則：

Δp=Δpf+Δpadd

(5)

以往研究中均根據文獻[2]的公式計算附加壓降或將引壓管中的附加壓降與實驗段中的附加壓降抵消，不僅增加了實驗誤差，而且使得計算過程復雜化。本文將振動附加力當作摩擦力的一部分，把摩擦壓降和附加壓降合并，稱為起伏振動摩擦壓降Δpfv，即：

Δp=Δpfv

(6)

振動摩擦阻力系數λv仍根據穩定狀態下的Dancy-Weisbach公式計算：

(7)

式中：D為管道直徑，m；ρ為流體密度，kg/m3；L為取壓孔間距，m；u為管道截面平均流速，m/s。

3 實驗結果分析

3.1 起伏振動對摩擦壓降的影響

文獻[10]將附加壓降進行抵消處理，結果表明搖擺運動引起摩擦壓降的波動，但搖擺工況的改變對平均摩擦阻力沒有明顯影響。文獻[16]沒有單獨考慮附加壓降，計算了起伏振動時液氫流動的平均摩擦壓降，發現振動會導致壓降的增大。但其中涉及相變問題，作者將壓降的增大歸因于管內氣相的增加。本實驗得出的D=15 mm、u=1.38 m/s、f=5 Hz、A=5 mm時起伏振動和穩定狀態下的摩擦壓降如圖2所示。結果表明，起伏振動摩擦壓降表現出明顯的類似正弦函數波動，波動范圍為平均值的22.8%～204.8%。此外，起伏振動摩擦壓降平均值為3.42 kPa，穩定狀態下摩擦壓降為0.69 kPa，起伏振動摩擦壓降平均值遠大于穩定狀態，這說明起伏振動顯著增加單相流動的沿程損失。這是因為起伏振動引起的附加力增大了管內流體微團間和管內流體與壁面間的碰撞，導致能量損失增大。

圖2說明起伏振動導致單相流動具有不穩定性，通過對摩擦壓降進行傅里葉分析得到起伏振動和穩定狀態下摩擦壓降的波動頻率，如圖3所示。由圖3可知，在起伏振動狀態下摩擦壓降波動有顯著的主頻分量，其他諧波分量可忽略不計，這說明起伏振動狀態下摩擦壓降表現出規律的周期性波動，而穩定狀態下的摩擦壓降不存在波動周期，此時摩擦壓降保持穩定。摩擦壓降波動中振動頻率分量比重最大，即摩擦壓降的波動頻率與起伏振動頻率一致。

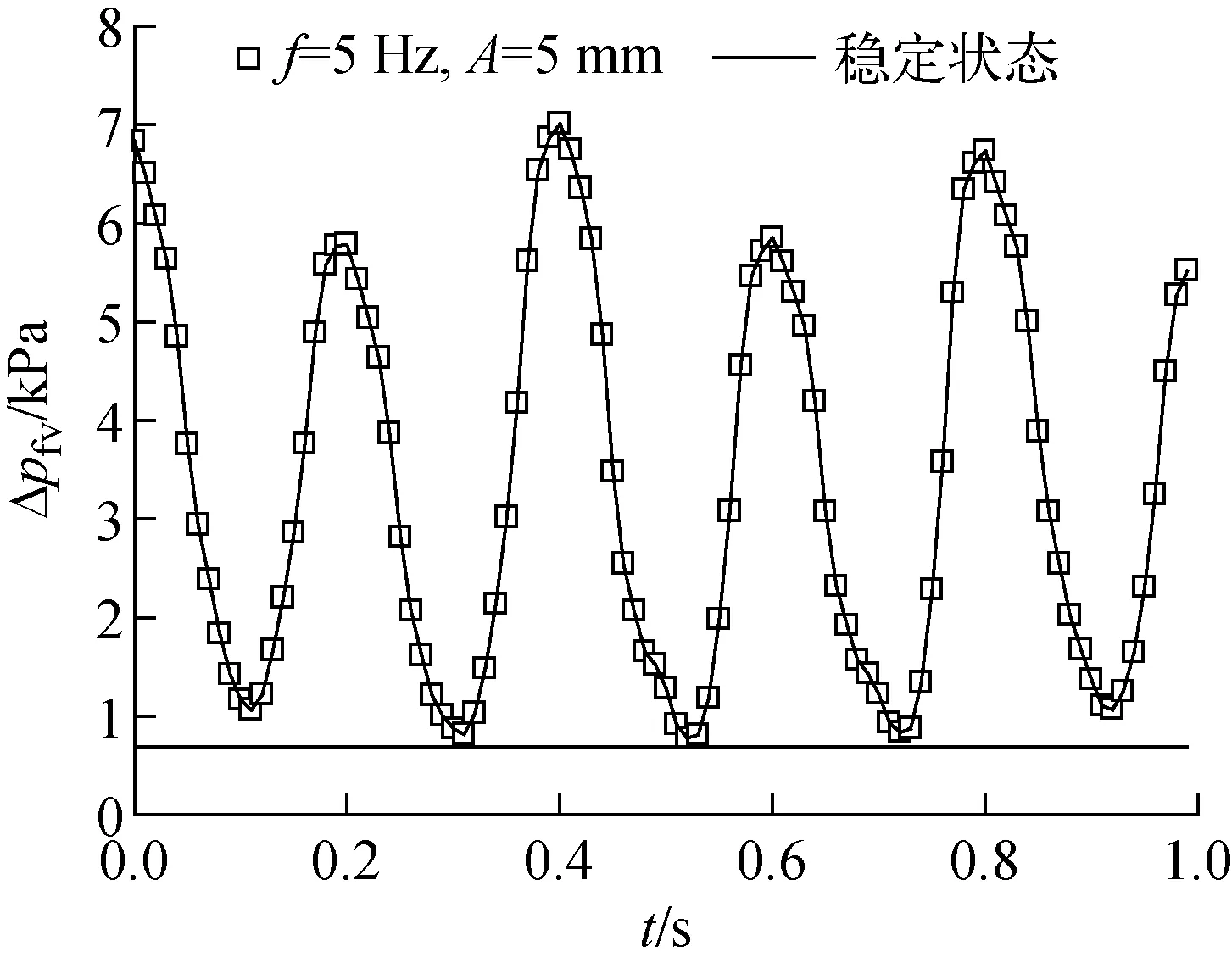
圖2 穩定狀態和起伏振動狀態的摩擦壓降對比Fig.2 Comparison of friction pressure drop between steady and undulating vibration conditions

圖4示出f=5 Hz、A=5 mm時摩擦壓降隨加速度的波動。由于實驗采用離心泵提供水頭，結合文獻[6]可得出采用離心泵提供水頭時瞬時流量不隨振動呈現周期性變化，因此摩擦壓降的周期性變化主要由振動引起的周期性作用力導致。將1個振動周期分為4個階段，管道的運動及管內流體微元受力如圖5所示。在1階段，管道從平衡位置向下運動，管內流體微元受力為向下的重力g和向上的附加力Fa的合力，隨振動加速度的增大，Fa逐漸增大，流體微元與管壁作用力減小，摩擦壓降減小，在1階段結束時摩擦壓降達到最小值。在2階段，管道從下限位置向上運動，管內流體微元受力為向下的重力g和向上的附加力Fa的合力，隨振動加速度的減小，Fa逐漸減小，流體微元與管壁作用力增大，摩擦壓降增大。在3階段，管道從平衡位置向上運動，管內流體微元受力為向下的重力g和向下的附加力Fa的合力，隨振動加速度的增大，Fa逐漸增大，流體微元與管壁作用力增大，摩擦壓降增大，在3階段結束時摩擦壓降達到最大值。在4階段，管道從上限位置向下運動，管內流體微元受力為向下的重力g和向下的附加力Fa的合力，隨振動加速度的減小，Fa逐漸減小，流體微元與管壁作用力減小，摩擦壓降減小。

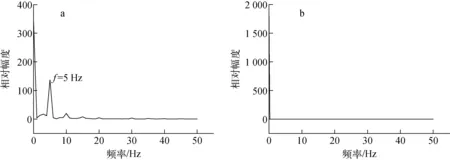
a——起伏振動狀態，f=5 Hz，A=5 mm；b——穩定狀態圖3 穩定狀態和起伏振動狀態的摩擦壓降波動頻率Fig.3 Friction pressure drop fluctuation frequency of steady and undulating vibration conditions

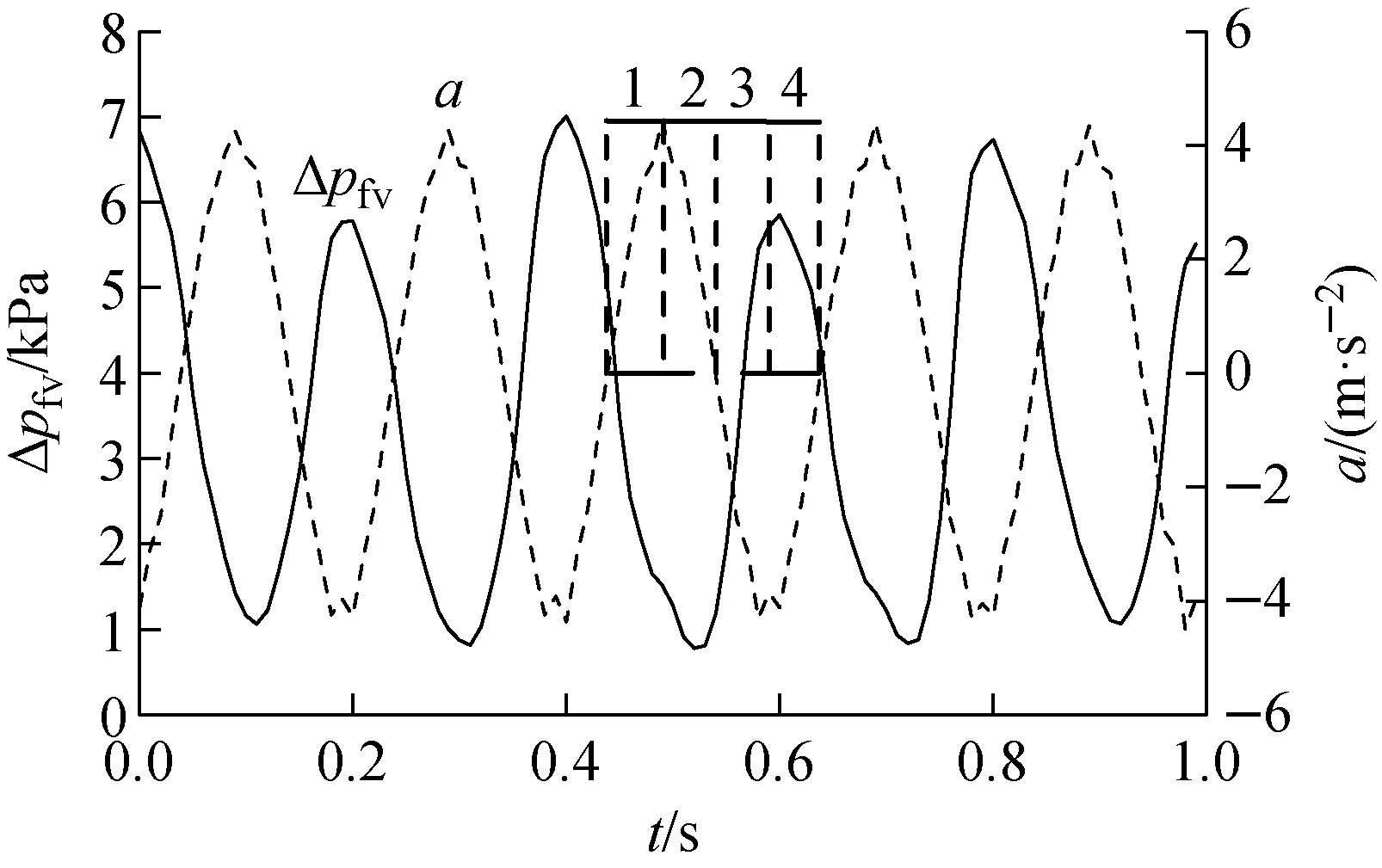
圖4 起伏振動下摩擦壓降與振動加速度的關系Fig.4 Relationship between friction pressure drop and vibration acceleration under undulating vibration

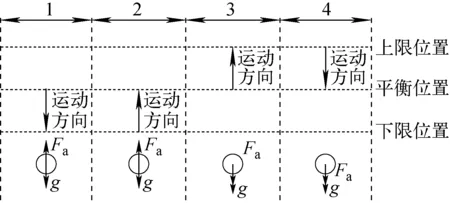
圖5 f=5 Hz時管道運動及管內流體微元受力分析Fig.5 Analysis of pipeline movement and micro-element stress of fluid in pipe with f=5 Hz

3.2 管徑對流動阻力特性的影響

f=5 Hz、A=5 mm、Re=27 900、D分別為15、20、25和30 mm時單相水的振動摩擦阻力系數波動如圖6所示。由圖6可知，隨管徑的變化，振動摩擦阻力系數λv的平均值有顯著變化。當D從15 mm增加至20 mm時，λv的平均值從0.028增至0.077，瞬時值相對于平均值的波動范圍無明顯變化。這是因為隨管徑的增大，管內水的波動程度增大，進而增大了能量損失，摩擦阻力系數增大。當D從20 mm增加至30 mm時，λv的平均值從0.077降至0.058，且當D=30 mm時λv的峰值表現為一高一低地變化，瞬時值相對于平均值的波動范圍有所減小。這是因為隨管徑的繼續增大，振動對流動的影響相對減小，導致λv的波動范圍和平均值有所減小。

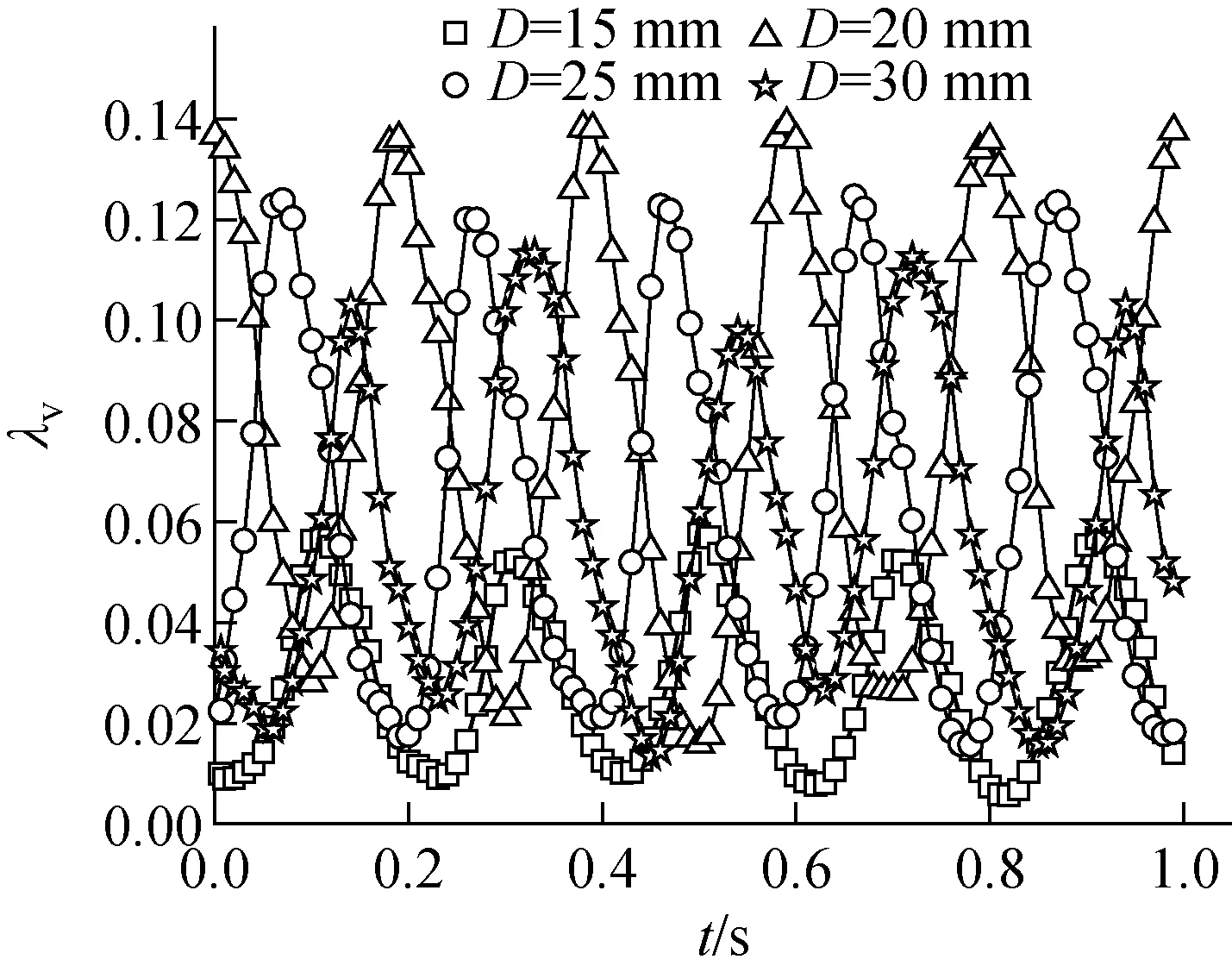
圖6 不同管徑下振動摩擦阻力系數的波動Fig.6 Fluctuation of vibration frictional resistance coefficient under different pipe diameters

3.3 傾角對流動阻力特性的影響

f=5 Hz、A=5 mm、D=15 mm、Re=35 160時不同傾角(θ)下振動摩擦阻力系數的變化如圖7所示。由圖7可知：當θ從10°增至24°時，λv平均值從0.042降至0.023；當θ從24°增至45°時，λv平均值從0.023降至0.02。這說明λv平均值隨傾角的增大而減小，隨傾角的增大，λv平均值的減小幅度降低。這是因為隨傾角的增大，振動附加力在垂直于壁面方向上的分力減小，對流動的影響削弱，使得振動摩擦阻力系數減小。

圖7 不同傾角下振動摩擦阻力系數的波動Fig.7 Fluctuation of vibration frictional resistance coefficient under different angles

3.4 雷諾數對流動阻力特性的影響

f=5 Hz、A=5 mm、D=15 mm時不同Re下的振動摩擦阻力系數的變化如圖8所示。由圖8可知：Re=20 600時，λv平均值為0.067；Re=35 160時，λv平均值為0.027。振動摩擦阻力系數與Re呈反比，這與穩定狀態下的摩擦阻力系數變化規律一致。此外，隨Re的變化，瞬時振動摩擦阻力系數的波動情況也有所不同。Re=20 600時，λv的波動范圍為平均值的22.8%～204.7%；Re=35 160時，λv的波動范圍為平均值的19.2%～183.6%。這說明隨Re的增加，λv的波動范圍減小。產生這種現象的原因是相同振動下，隨Re的增加，振動附加力對流動的影響減小，進而使得λv的波動范圍減小。

圖8 不同Re下振動摩擦阻力系數的波動Fig.8 Fluctuation of vibration frictional resistance coefficient at different Re

3.5 起伏振動頻率對流動阻力特性的影響

由式(3)可知，振動加速度與振動頻率的平方呈正比，振動頻率的改變會嚴重影響振動附加力，進而改變振動摩擦阻力系數。D=20 mm、Re=27 826、A=5 mm時不同振動頻率下振動摩擦阻力系數的變化如圖9所示。由圖9可知，相同振幅下振動頻率的改變會引起振動摩擦阻力系數的平均值和波動規律的變化。當f由2 Hz增至5 Hz，λv的平均值由0.029增至0.076，λv的波動范圍由19.5%～207.9%變化至20.7%～183.4%；當f由5 Hz增至8 Hz，λv的平均值由0.076降至0.034，λv的波動范圍由20.7%～183.4%變化至4.1%～304.1%。

這種變化產生的原因可用圖5的受力分析解釋。當振動頻率較低時，振動附加力較小，此時水和管道同步振動。隨振動頻率的增大，水的縱向運動加劇，能量損失增大，導致摩擦壓降的增大。同時隨振動頻率的增大，水的運動方向改變速度加快，同一方向上的力持續作用時間減小，導致振動摩擦壓降的波動幅度減小。當振動頻率較大時，振動附加力較大，此時水和管道的運動不同步。隨振動頻率的增大，水在振動附加力和慣性的作用下會持續一段時間集中于管道中間，水和管道壁面的作用力很小，振動摩擦壓降會在低位保持一定的時間，如圖9所示。當水在管道中間的狀態結束后，水的運動和管道運動疊加，導致摩擦壓降迅速增大到最大值。

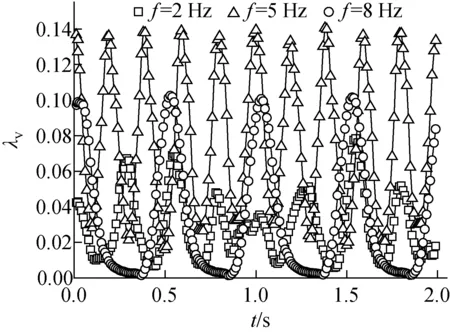
圖9 不同振動頻率下振動摩擦阻力系數的波動Fig.9 Fluctuation of vibration frictional resistance coefficient at different vibration frequencies

3.6 振幅對流動阻力特性的影響

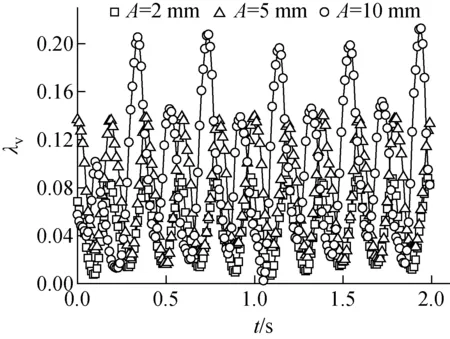
圖10 不同振幅下振動摩擦阻力系數的波動Fig.10 Fluctuation of vibration frictional resistance coefficient at different amplitudes

振幅的改變同樣會引起振動附加力的變化，進而改變振動摩擦阻力。D=20 mm、Re=27 826、f=5 Hz時不同振幅下振動摩擦阻力系數的變化如圖10所示。由圖10可知，A從2 mm增至10 mm時，λv的平均值從0.045增至0.092。這是因為振動附加力與振幅的一次方呈正比，隨振幅的增大，振動加速度增大，但并不能引起水與管道的相對運動狀態的變化，僅使得管內水與壁面的作用力增大，導致振動摩擦阻力系數的增大。

4 起伏振動狀態下單相水摩擦阻力系數計算

由以上分析可看出，起伏振動狀態下的振動摩擦阻力系數周期性波動比較明顯，不能用穩定狀態下的計算模型計算，需要提出適用于起伏振動狀態的振動摩擦阻力系數計算公式。通過以上分析可得出振動摩擦阻力系數主要與搖擺狀態(a，v)、Re和當量直徑有關，根據量綱分析中的π定理可導出振動摩擦阻力系數的表達式。起伏振動狀態下單相流振動摩擦阻力特性物理方程為：

F(Δpfv,μ,ε,a,v,D,L,ρ,u,θ)=0

(8)

式中：μ為流體的動力黏度，N·s/m2；ε為管道粗糙度，m。

本研究試驗管段為光滑有機玻璃管，忽略粗糙度的影響，則振動摩擦壓降為：

(9)

起伏振動狀態下的振動摩擦阻力系數可表示為：

(10)

通過對影響因素和大量數據分析，最終將振動摩擦阻力系數寫為如下形式：

(11)

為了分析振動對流動特性的影響，定義振動雷諾數Rev如下：

(12)

式中，vv為振動平均速度，由下式計算：

vv=4vmf

(13)

式中，vm為起伏振動速度最大值。

通過對大量實驗數據進行擬合，得到式(11)中c1、c2和c3的關系式為：

(14)

本文得出的起伏振動狀態下振動摩擦阻力系數計算值和實驗值的對比如圖11所示。從圖11可明顯看出，該關系式能較準確地計算振動摩擦阻力系數。在峰值和谷值由于波動較劇烈，實驗測量值隨機性較大，因此關系式誤差較大，在中間位置的擬合誤差均在10%以內。該關系式的適用范圍為f<8 Hz、A<10 mm、4 6878 Hz的情況，并且在實際應用中幾乎不存在這種高頻率振動，因此水和管道振動異步情況下的振動摩擦阻力系數計算模型還有待進一步研究。該關系式的適用范圍有限，主要為非穩定狀態下振動摩擦阻力的計算提供一種分析思路。

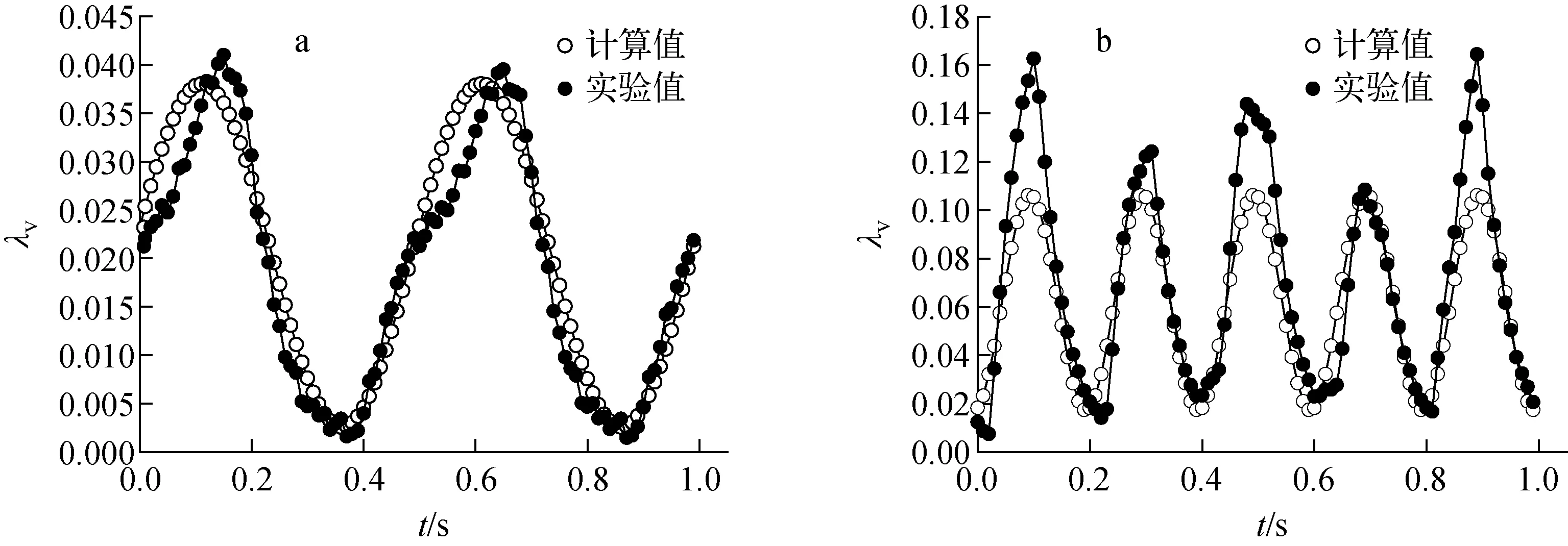
a——D=15 mm，Re=20 645，f=2 Hz，A=5 mm；b——D=15 mm，Re=20 645，f=2 Hz，A=10 mm圖11 振動摩擦阻力系數計算值和實驗值的比較Fig.11 Comparison of calculated value and experimental valueof vibration frictional resistance coefficient

5 結論

本文采用實驗方法對單相水振動摩擦壓降進行研究，主要得出以下結論。

1) 起伏振動狀態下單相水的摩擦壓降呈周期性波動，且摩擦壓降平均值較穩定狀態大。

2) 相同起伏振動條件下，Re越大，振動摩擦阻力系數的平均值和波動范圍越小；振動摩擦阻力系數與傾角呈反比。管徑對振動摩擦阻力系數的影響較復雜，當管徑從15 mm增至20 mm時，振動摩擦阻力系數平均值顯著增大；當管徑從20 mm增至30 mm時，振動摩擦阻力系數平均值降低。

3) 由于振動附加力和重力的相互影響，振動摩擦阻力系數平均值隨振動頻率的增大先增大后減小。振動摩擦阻力系數平均值隨振幅的增大而增大。

4) 得出了振動摩擦阻力系數的經驗公式，與實驗值吻合較好，為起伏振動狀態下振動摩擦阻力的計算提供了新思路。