基于時間反轉的多用戶差分混沌鍵控方案

張 剛，趙暢暢，張天騏

(重慶郵電大學 信號與信息處理重慶市重點實驗室， 重慶 400065)

自1963年首次發現混沌系統至今，混沌及其應用處于不斷飛速發展中[1].作為非線性科學中的一個重要組成部分，混沌理論的研究及其應用已然成為一個誘人的研究方向，將混沌機制應用于通信方面更是吸引了大量的學者.混沌信號作為載波去調制信息信號具有以下兩方面的優勢：① 其寬頻特征能達到某些方面上的頻譜擴展；② 混沌信號運動軌跡的無規則性、非周期性、良好的自相關性與互相關性及其不可預測性為所傳輸的信息提供了保密性，所以將混沌信號作為調制信息信號的載體在保密通信中具有很大的實際應用價值[2-5].混沌數字調制技術作為在保密通信中的一種典型應用，主要是運用非周期的混沌信號代替傳統的數字通信中的正弦載波，利用其寬頻特性實現了頻譜擴展[6-7].而且，根據在接收端是否需要同步技術，這項數字調制技術可以分為相干解調和非相干解調兩種方式.

相干解調的系統中，在接收方恢復出精確的參考信號是一種必然的需求，而目前的技術很難達到此目的，限制了采用相干解調系統的發展[8].但是，采用非相干解調的系統在接收端進行解調時不需要同步技術.因此，在混沌數字調制系統中，將非相干檢測應用于系統中很普遍，其中數差分混沌移位鍵控 (DCSK)[9]和相關延遲移位鍵控(CDSK)[10]的應用最為廣泛，目前的混沌鍵控調制系統大都是在這兩種系統上進行完善.在DCSK系統中，每比特持續時間被分成兩個相等的時隙，但只有一半的時隙用來傳輸信息信號，因此降低了系統的傳輸效率.CDSK在一個幀周期內將參考信號和信息承載信號疊加后一起傳輸，雖然提高了系統的傳輸效率，但是降低了系統的誤碼性能.針對上述的問題，楊華等[11-12]提出了雙倍速調制DCSK(DBR-DCSK)和參考信號調制DCSK(RM-DCSK)系統來提高系統的安全性以及傳輸信號的快慢.Kaddoum等[13]在2015年提出I-DCSK系統，利用時間反轉產生與數據承載信號正交的參考信號，將兩個信號疊加后一起發送，提升了系統的傳輸速率.

文獻[14]中提出的可變延遲多址(VDMA)通信系統，利用每個用戶的混沌參考信號和信息信號之間延遲時間的不同來區分不同的用戶，以達到傳輸多用戶的目的.但是，該系統的誤碼性能并沒有得到改善，并且需要大量的延遲電路.2016年，張剛等[15]提出一種改進型多用戶正交差分混沌鍵控(MA-ODCSK)系統，利用Walsh碼使傳輸的每路信息承載信號之間嚴格正交，減少了信號間的干擾，從而達到使系統誤碼性能變好的目的，但系統的傳輸速度受到Walsh階數的影響.

為了降低DCSK系統的誤碼率，本文提出了一種基于時間反轉的多用戶差分混沌鍵控(TRM-DCSK)系統.該系統利用時間反轉將兩路信息信號在每根延遲線后疊加在一起傳輸，達到傳輸2 bit信息信號的目的.對TRM-DCSK系統在AWGN信道及Rayleigh衰落信道中進行實驗仿真，結果表明：傳輸相同用戶數時，TRM-DCSK系統的誤碼性能比傳統多用戶系統好，而且沒有增加系統的復雜性，具有較好的應用前景.

1 TRM-DCSK系統原理

TRM-DCSK 方案發射端的結構如圖1所示.圖中：xi為經過符號函數后的混沌信號；yi為混沌信號發生器的輸出信號；β為擴頻因子；M為延遲線的數量；bi為信息信號；si為發射端信號.

該系統采用Logistic映射[16]生成一段長度為β的混沌序列yi，再經過符號函數形成比特能量恒定的混沌信號xi，如下式所示：

(1)

yi∈(-1,1)，xi∈{-1,1}

i=1,2,…,β

xi的均值E(xi)=0,方差var(xi)=1.

在TRM-DCSK系統中，首先將發送的混沌信號xi作為參考信號，然后在每根延遲線后的信息時隙中利用時間反轉來區別不同的用戶，使每路延遲線后均可傳輸2 bit的信息信號.該系統的幀結構如圖2所示，其中第k幀內的傳輸信號表達式為

(2)

TRM-DCSK系統的平均比特能量為

(3)

為了恢復出所傳輸的信息比特，將接收到的信息信號ri與延遲相應時間間隔后的信號取相關，可以恢復出此路延遲中的第1個用戶，再讓延遲后的信號經過時間反轉與接收到的信號取相關，即可恢復出此路延遲中的第2個用戶.TRM-DCSK系統接收端的結構如圖3所示.

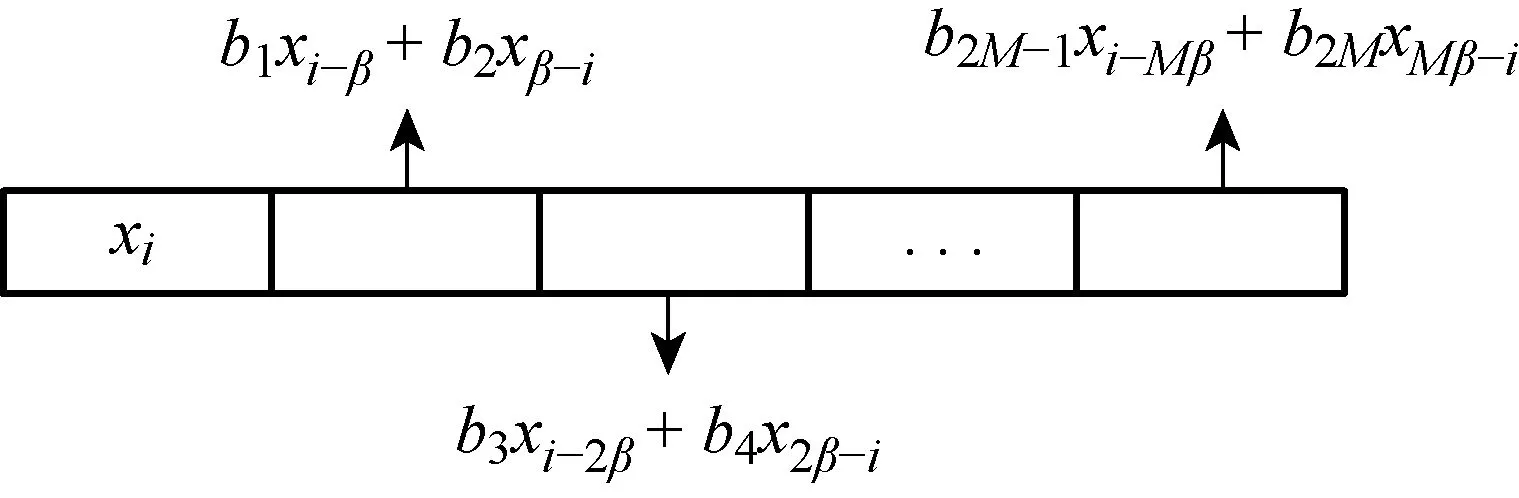
圖2 TRM-DCSK系統幀結構Fig.2 TRM-DCSK frame format

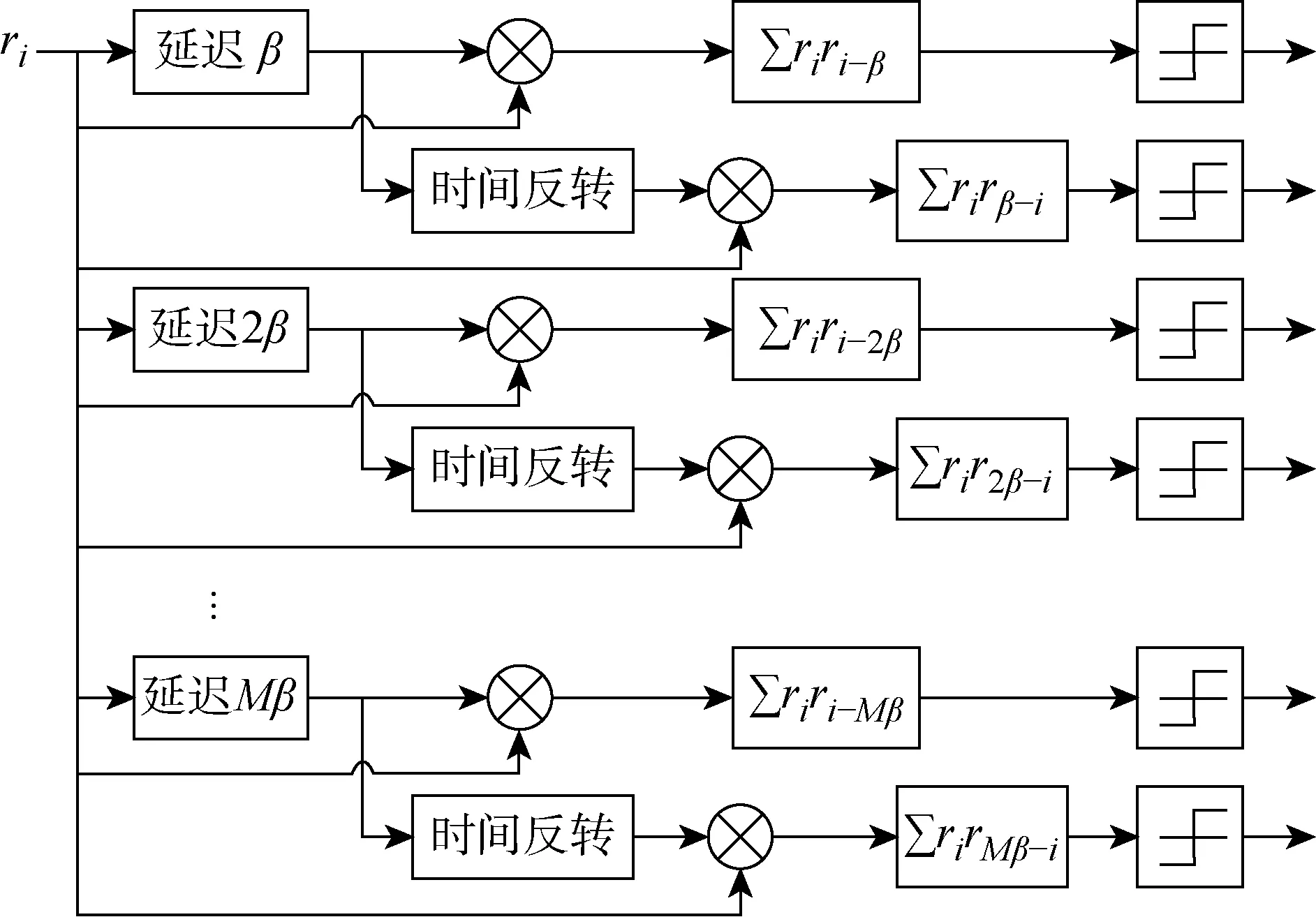
圖3 TRM-DCSK系統接收端框圖Fig.3 Receiver block diagram of the TRM-DCSK

為了解調TRM-DCSK系統中第k幀的信息信號，分兩種情況進行討論.

(1) 當解調第2m-1(m=1,2,…,M)個用戶的信息時，輸出的判決變量為

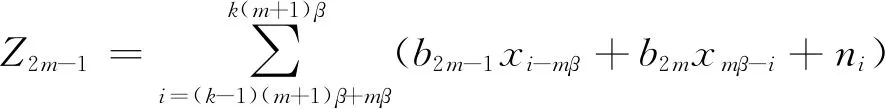
(xi-mβ+ni-mβ)

(4)

式中：ni是均值為0，方差為N0/2的高斯白噪聲.

(2) 當解調第2m個用戶的信息時，輸出的判決變量為

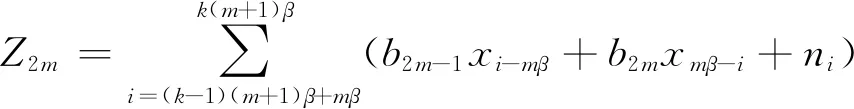
(xmβ-i+nmβ-i)

(5)

根據下式的判決準則，可以恢復出信息信號b2m-1和b2m：

(6)

圖4所示為DCSK系統和TRM-DCSK系統的平方幅度譜.從圖4可以看出， DCSK的平方幅度譜在歸一化比特頻率為奇數時近似為0，原因在于該系統所傳輸的信息信號與參考信號相同或者相反.平方后的信息信號與參考信號在比特頻率為奇數時的頻譜分量相互抵消，降低了安全性.TRM-DCSK系統在信息時隙中傳輸的信號與參考時隙中的信號不相似，圖4也顯示出該系統的平方幅度譜具有類噪聲性，保密性比較好.

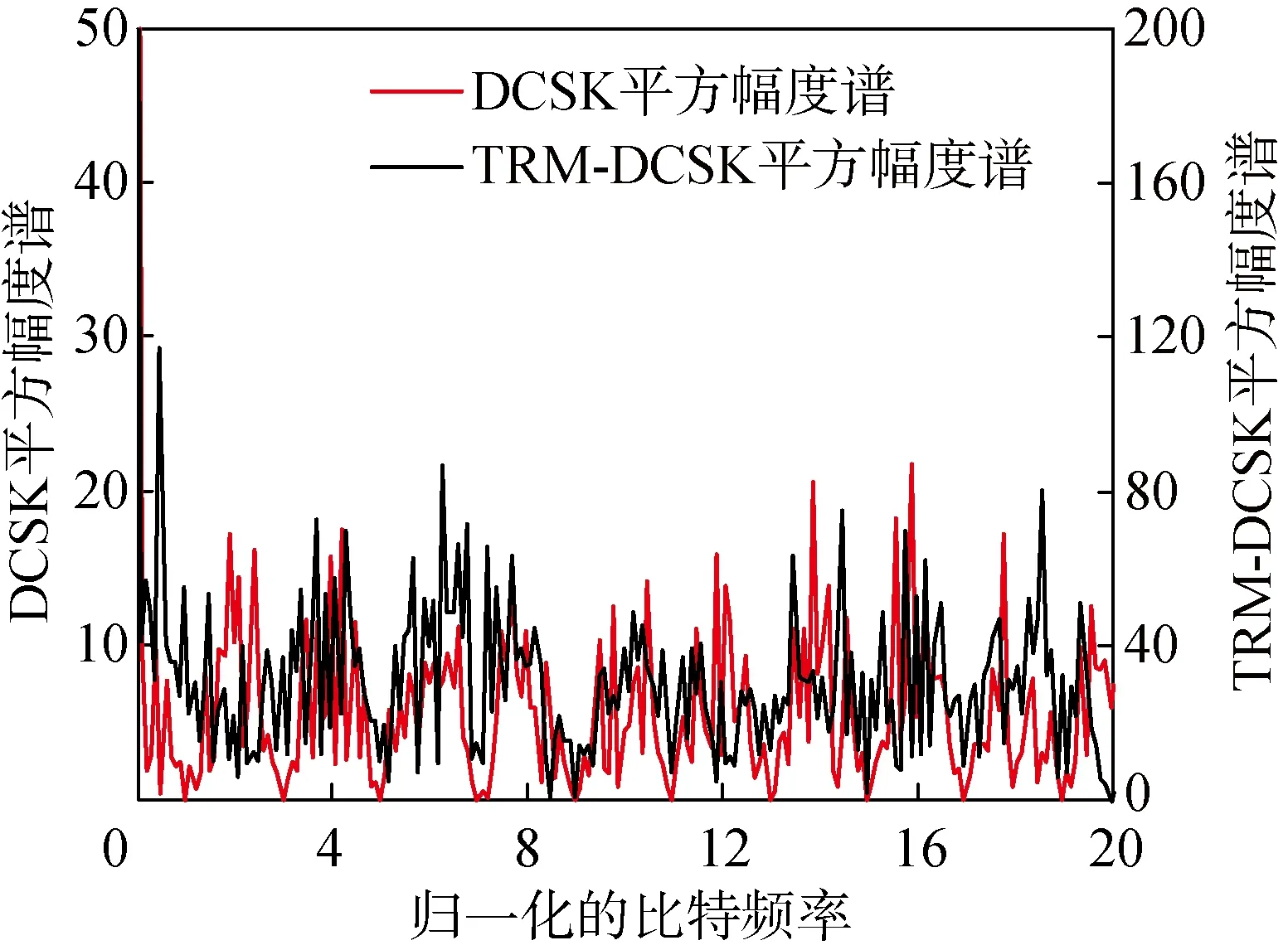
圖4 DCSK和TRM-DCSK平方幅度譜Fig.4 DCSK and TRM-DCSK squared amplitude spectra

2 TRM-DCSK系統性能分析

本節推導TRM-DCSK在高斯信道及兩條獨立的Rayleigh衰落信道下的誤碼率(BER)公式.瑞利衰落信道模型如圖5所示.圖中：α1和α2為滿足兩徑Rayleigh衰落的隨機變量；τ為兩條路徑之間的延遲且τ?β.

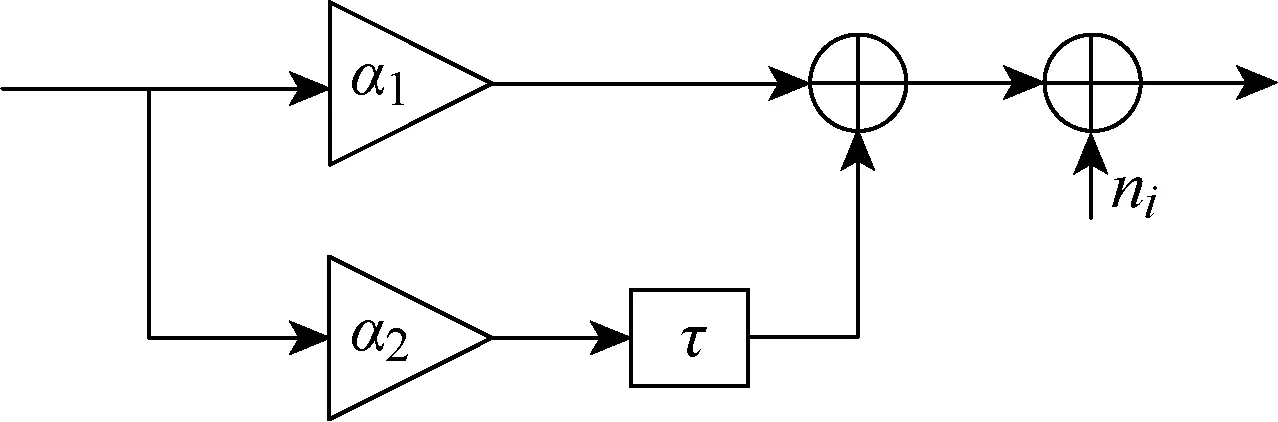
圖5 兩徑Rayleigh衰落信道結構Fig.5 Two-path Rayleigh fading channel structure

假設在1個時隙的時間內，信道系數保持不變，發送的信號經過Rayleigh衰落信道傳輸后，則有

ri=α1si+α2si-τ+ni

(7)

對第k幀內的第2m-1個用戶和第2m個用戶進行解調，以第2m-1個用戶為例進行分析.由式(7)得TRM-DCSK系統的輸出判決變量為

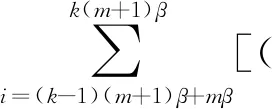
α2b2m-1xi-mβ-τ+α2b2mxmβ-i-τ+ni)×

(α1xi-mβ+α2xi-mβ-τ+ni-mβ)]=

A+B+C

(8)

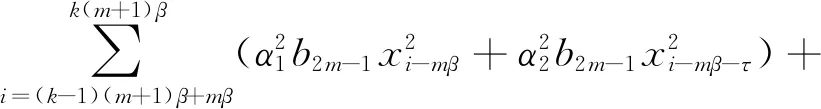
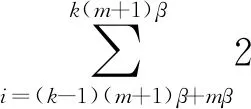
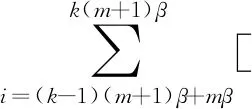
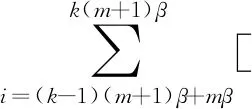
α1b2m-1xi-mβni-mβ+α1b2mxmβ-ini-mβ+

α2b2m-1xi-mβ-τni-mβ+α2b2mxmβ-i-τni-mβ]

式中：A中前兩項為有用信號項，后幾項為用戶間干擾項；B及C為噪聲干擾項.由于 Logistic 映射的自相關旁瓣為0，使得B中的

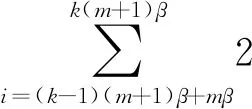
降低了信號間的干擾，所示降低了系統的誤碼率.

利用高斯近似法推導TRM-DCSK在Rayleigh衰落信道中的誤碼率公式時，都是在以下假設條件下實現的：① 發送的二進制數據“+1”和“-1”是等概率出現的； ②ni是均值為零，方差為N0/2的高斯白噪聲，對于i和j，ni不僅與xi互不相關，并且當i≠j時，ni與nj也互不相關.

基于以上假設，誤碼率公式具體推導過程為

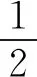
(9)

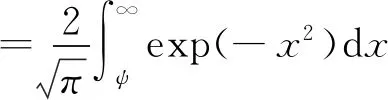
E(Z2m-1)=E(A)+E(B)+E(C)=

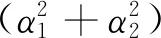
(10)

var(Z2m-1)=var(A)+var(B)+var(C)+

2Cov(A,B)+2Cov(A,C)+2Cov(B,C)=

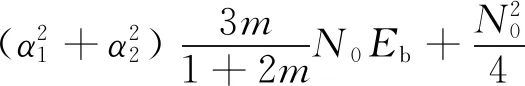
(11)

式中：Cov表示協方差，

Cov(A,B)=Cov(A,C)=Cov(B,C)=0

由式(9)～(11)可以求得TRM-DCSK系統在第k幀內第2m-1個用戶的誤碼率公式為

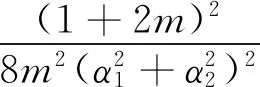
(12)

同理可求得TRM-DCSK在第k幀內第2m個用戶的BER公式為

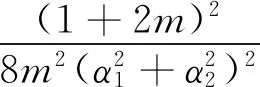
(13)

TRM-DCSK系統在第k幀內任一用戶的誤碼率公式即為式(12).

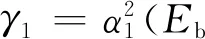
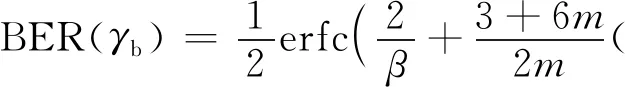
(14)

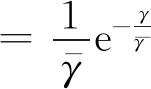
(15)

γb=γ1+γ2服從以下分布：

f(γb)=

(16)

根據式(14)和(16)，可求得平均誤碼率的表達式為

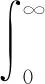
(17)

在式(12)中令α1=1，α2=0，得到TRM-DCSK系統在AWGN信道中的誤碼率公式為

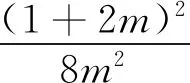
(18)

3 TRM-DCSK系統仿真分析

從式(18)可以看到，β、m及Eb/N0均對TRM-DCSK的BER產生一定的影響.本節對TRM-DCSK 系統在AWGN信道以及Rayleigh衰落信道中進行Monte Carlo 實驗仿真.所有仿真曲線值均為106次仿真結果取平均值的前提下得到.為了敘述簡潔，以N(N=2m)表示系統傳輸的用戶數.

3.1 AWGN信道下系統的仿真分析

圖6(a)所示為N=4，β=128,256,512時，TRM-DCSK系統的BER隨Eb/N0變化的規律.從圖中可以看出，系統的Monte Carlo 仿真和理論公式(18)的仿真基本一致，表明了理論推導公式的正確性.當Eb/N0=12 dB時，相較于β=256，128時BER的值較小，表明TRM-DCSK的誤碼性能隨β的增加而變差.原因在于，隨著β的增大，在判決變量中引入的噪聲干擾項增多.當β=128時，該系統的誤碼性能隨Eb/N0的增加而變好.

圖6(b)所示為N=4,6,12時，TRM-DCSK系統的BER隨Eb/N0變化的規律.可以看出，系統的Monte Carlo 仿真與公式的理論值一致.Eb/N0=12時，相較于N=6，12時系統的BER較小，這表示系統的誤碼率隨著N的增大而減小，即系統的誤碼性能變好.造成這種現象的原因有兩方面：① 從式(3)可知，隨著N的增多，系統的平均比特能量降低；② 由TRM-DCSK系統的幀結構可以看出，隨著N增大，系統的信息時隙增多，所需要傳輸的信息信號在整個系統的幀結構中所占的比重增加.

圖7所示為當Eb/N0=11,13,16及N=12時，系統的誤碼性能隨β增加而變化的規律.當β<100時，TRM-DCSK系統的仿真值與理論值并不吻合.這是由于β較小時，相關器輸出的變量并不完全服從高斯分布[17]，所以理論值與仿真值之間存在偏差.當Eb/N0固定時，TRM-DCSK系統的BER會隨著β的增加先減小后增大，即存在一個最合適的β使TRM-DCSK的誤碼性能達到最佳狀態.

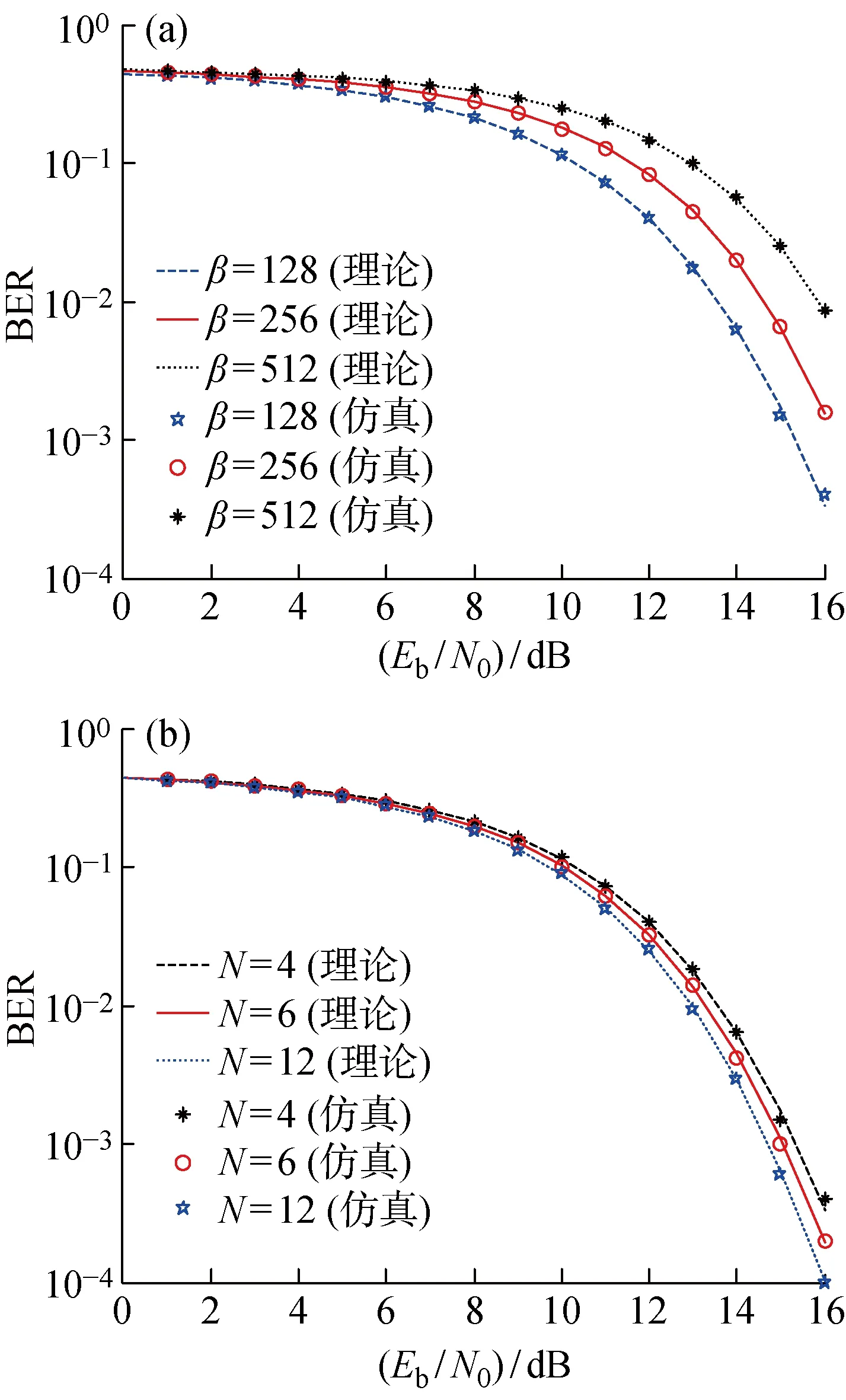
圖6 TRM-DCSK系統理論值與Monte Carlo仿真比較Fig.6 Comparison of experimental and theoretical values of TRM-DCSK system

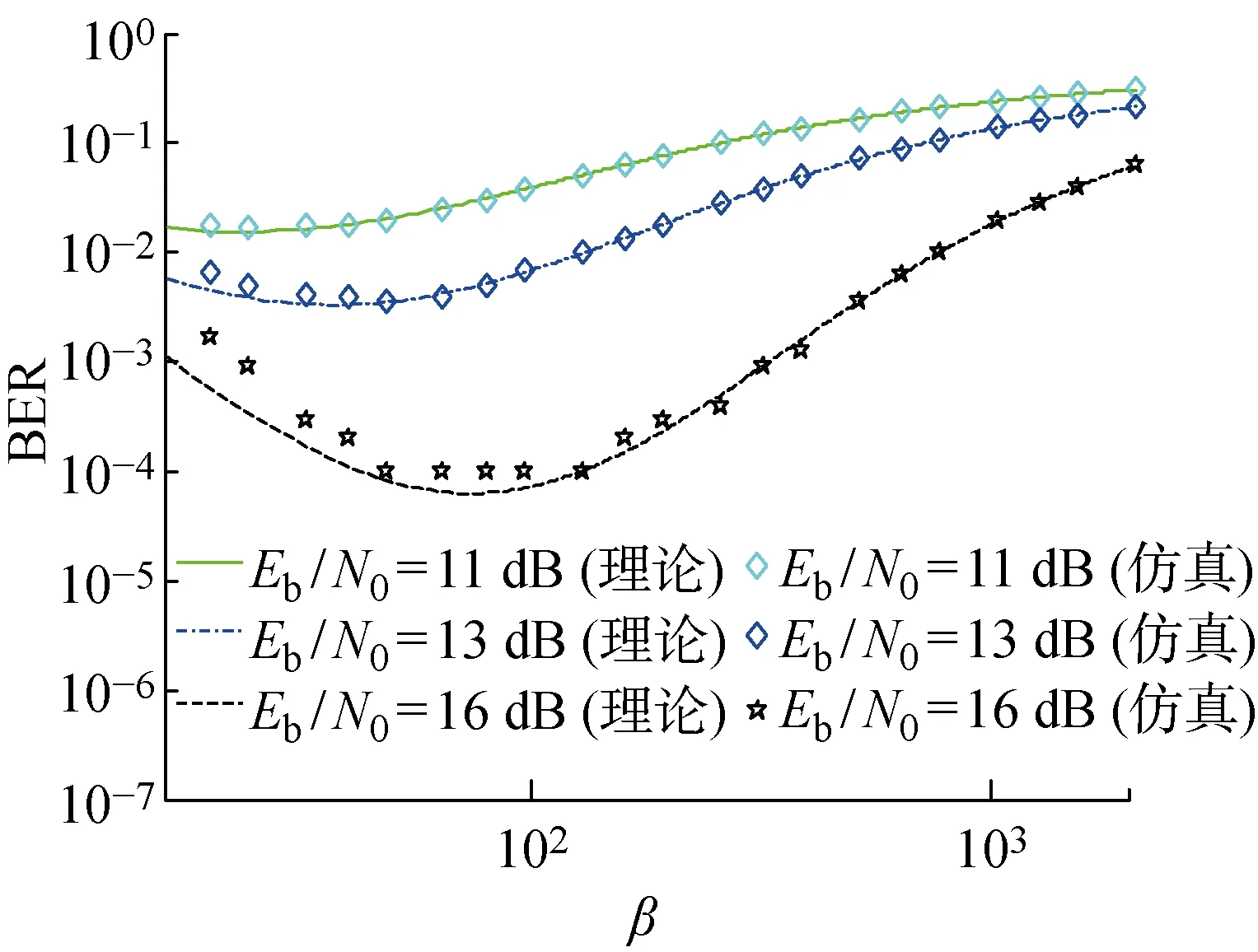
圖7 系統BER隨β變化的性能曲線Fig.7 The system BER curve with different values of spreading factor β

圖8所示為系統BER在Eb/N0=11,13,16時，系統誤碼性能隨N增加而變化的曲線.圖6(b)中已對TRM-DCSK系統誤碼性能隨N的增大而改善進行了解釋.此外，從式(18)可以看出，當系統的N增大到一定值時，系統的BER會趨于穩定.

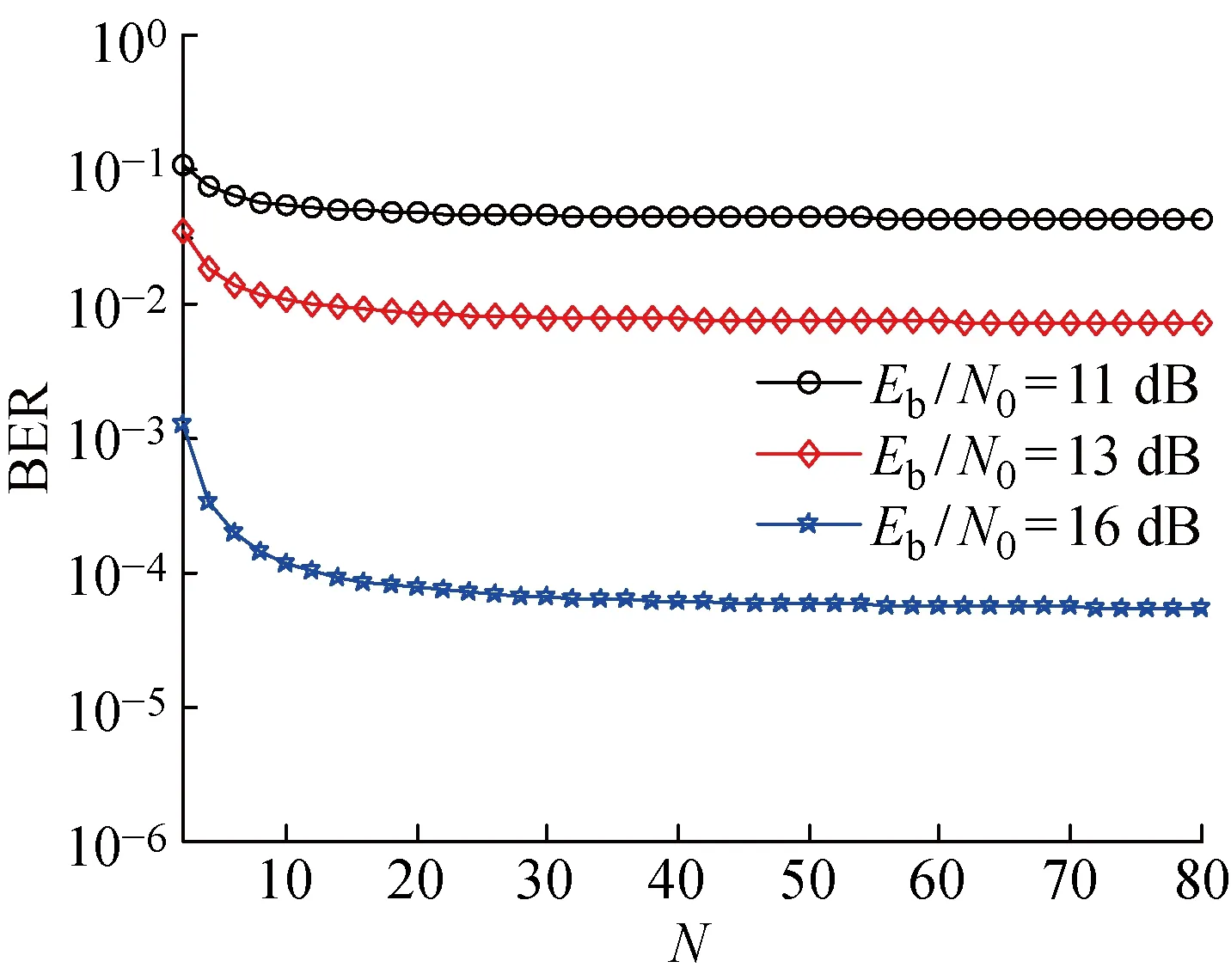
圖8 系統BER隨N變化的曲線Fig.8 The system BER curve with different users N

圖9所示為N=4且β=128,256時，TRM-DCSK與VDMA-DCSK及MU-SSDCSK系統的誤碼率隨Eb/N0增加而變化的規律.可以看到，當β相同時，相較于MU-SSDCSK系統，TRM-DCSK系統的BER較小.原因在于，TRM-DCSK系統利用時間反轉，減少了信號與噪聲之間的干擾項，并且在發射端加了符號函數，使比特能量恒定.

3.2 Rayleigh信道下系統的仿真分析

為分析TRM-DCSK系統在Rayleigh衰落信道下的誤碼性能，根據式(17)討論在兩種不同路徑增益下的誤碼性能.

情況1兩條獨立路徑的平均能量增益相等，即

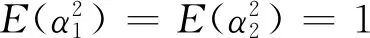
(19)

情況2兩條獨立路徑的平均能量增益相差為10 dB，即

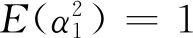
(20)

圖10所示為N=8，β=128,256時，Rayleigh衰落信道中TRM-DCSK系統在兩種不同的獨立路徑增益下的BER隨Eb/N0增加而變化的規律.可以看出，TRM-DCSK系統的Monte Carlo仿真與理論公式(17)的結果大致吻合，而且在相同的混沌序列情況下，情況1信道的誤碼率比情況2信道的誤碼率低，即情況1的誤碼性能比情況2誤碼性能好.

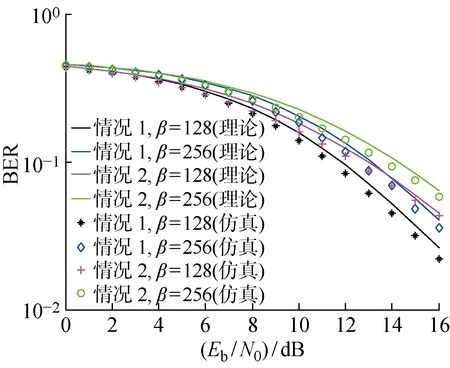
圖10 TRM-DCSK系統在兩種增益下的仿真比較Fig.10 Simulation comparison of TRM-DCSK system under two kinds of gain

圖11所示為N=4，β=128時，TRM-DCSK與MU-SSDCSK在Rayleigh信道下的BER隨信噪比的增加而變化的規律.可以看出，在Eb/N0相同的情況下，系統在情況1信道下的誤碼性能比在情況2信道下的誤碼性能好，并且在情況1信道下的誤碼性能總是比情況2信道下的誤碼性能好10 dB左右.N相同時，系統的誤碼率相對于MU-SSDCSK系統有所降低，但是兩系統在相同情況下的差距并沒有在AWGN信道中的明顯.

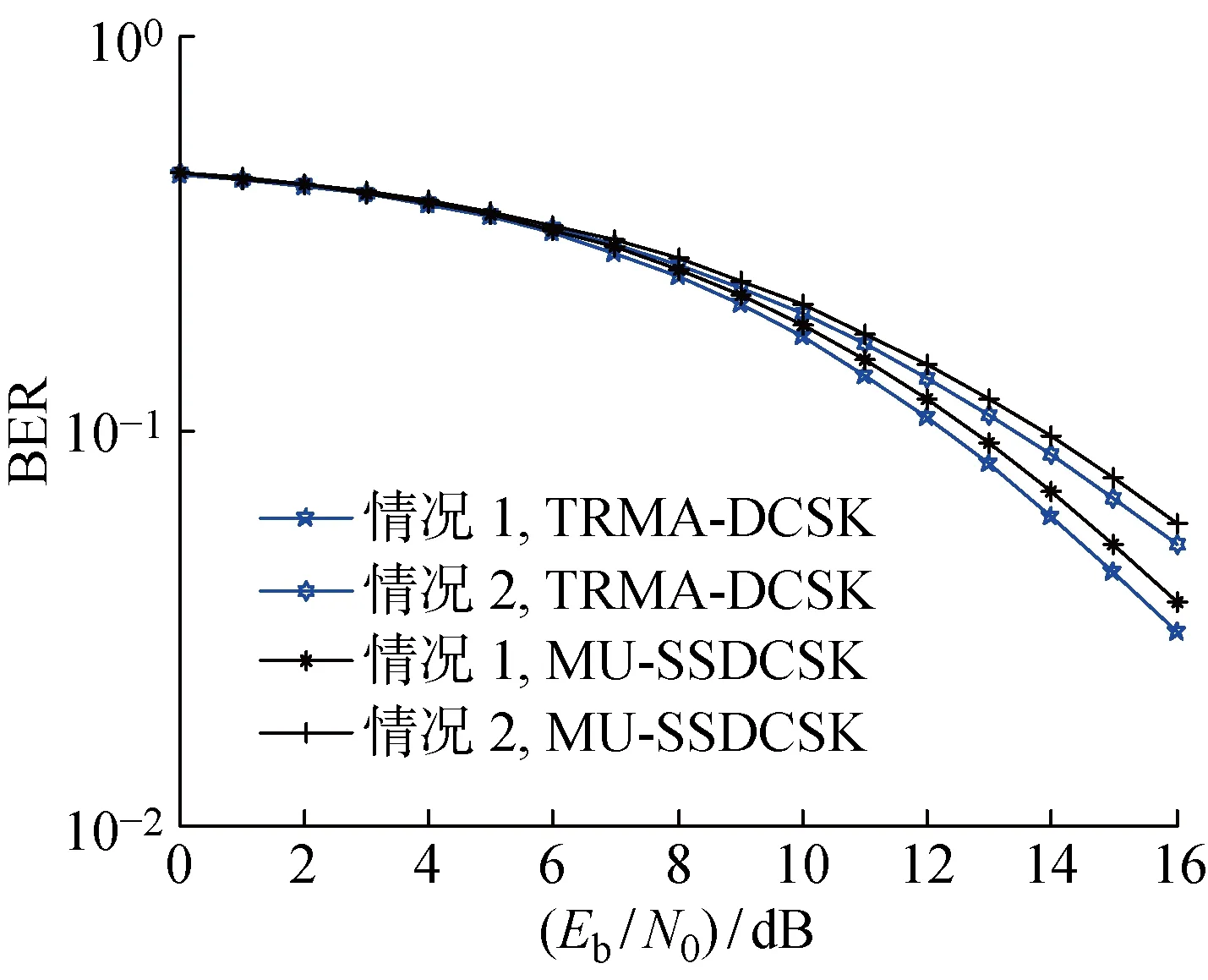
圖11 Rayleigh信道中不同系統性能對比圖Fig.11 BER performance comparison of different systems in Rayleigh channel

4 結語

基于DCSK系統的研究基礎，本文給出了一種利用時間反轉技術來改善系統誤碼性能的多用戶DCSK方案.詳細介紹了TRM-DCSK系統的幀結構及在發送端和接收端的框圖，且通過高斯近似法推導了系統在AWGN信道和Rayleigh信道下的誤碼率公式.通過仿真對比該系統與MU-SSDCSK系統的誤碼性能，發現該系統可以降低信號與噪聲之間的干擾，可以提升多用戶DCSK方案的誤碼性能，具有很好的應用價值.