“獵狗追免”輕松解

楊弘

學生：“獵狗為什么總是追兔子？”

老師：“大概是為奧數題作貢獻吧！”

學生：……

行程單位統一

是獵狗追兔的解題關鍵。

獵狗追兔是奧數中行程問題的一種，同時也是數學行程問題中的一種，它與一般的行程問題有著某種相通性。

問題敘述：

兔子動作快、步子小;獵狗動作慢、步子大。通常我們遇到的行程問題中所給路程都是通用單位（米或千米）等，但這類題中狗步與兔步是不一樣的單位，所以要先統一單位，然后利用追及問題公式“路程差÷速度差=追及時間”來解出答案。

舉例說明：

①相同路程內，獵狗跑4步（狗步）=兔子跑7步（兔步），可以求出狗步與兔步的比;②相同時間內，兔子跑3步（兔步）=獵狗跑2步（狗步），可以求出兔子與獵狗的速度比，即單位時間內獵狗和兔子分別跑多少兔步（或狗步）。

關鍵：

統一為狗步或兔步。

規則：

要視路程差的單位而定，若路程差的單位為狗步則速度要統一為狗步，反之統一為兔步。

記住這些，“獵狗追兔”問題自然迎刃而解！

元宵佳節猜燈謎，果然，元宵佳節一到，老爸就不懷好意地對著我笑：“嘿嘿嘿……嘿嘿嘿……”我立刻警惕起來，老爸，又憋著什么壞呢？

“今年元宵節咱們玩個好玩的，猜燈謎！”老爸微微一笑。

猜燈謎，這可是我的強項。不過以我對老爸的了解，事情恐怕沒這么簡單。果然，老爸話鋒一轉，說道：“不過，文字燈謎大家早都玩膩了，咱們不如換一個數學的玩法。”

“NO～～～～！”我慘嚎一聲，不過看著老爸晃得叮當響的元宵，只好放手一搏了。

燈謎一：高個子和矮個子兩個小朋友走一段路程，通常誰先到達終點？

我想了想，說道：“身高有差異的兩個小朋友走同一段路程，通常是個子高的走得比較快，因為個高的小朋友步子比較大。”

爸爸笑著點點頭：“沒錯，所以影響速度的第一個因素是‘步長。”

燈謎二：如果高個子和矮個子兩個小朋友走同一段路程，個子矮的有沒有可能先到達終點，為什么？

有了第一個問題墊底，第二個問題思考起來就簡單多了。我的答案是：有可能，如果個子矮的小朋友在單位時間內走的步數比較多，也可說單位時間內腳落地的次數多，那么個子矮的小朋友可能會先到達終點。

爸爸豎起了大拇指，說道：“沒錯，這就是影響速度的第二個因素——‘步頻。速度與步長和步頻之間的關系就是：

速度=步長×步頻。”

燈謎三：兔跑8步的時間狗跑5步，兔跑9步的距離等于狗跑4步的距離，兔和狗的速度比是多少？

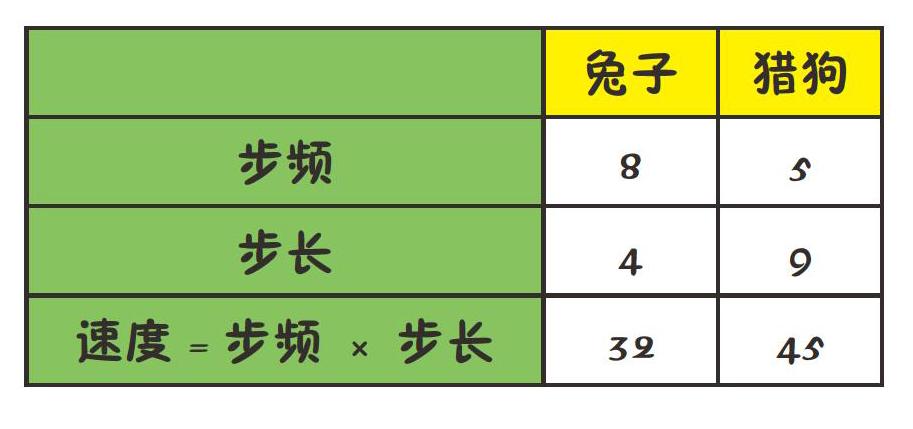
看著題，我拿出紙筆寫出計算思路，并列出表格：

相同時間內，兔跑8步，狗跑5步……可以理解成相同時間內，兔子腳落地次數為8，獵狗腳落地次數為5。所以可以得到兔子和狗的步頻之比為8：5;

相同路程內，兔跑9步，狗跑4步……可以假設距離為36，那么兔子的一步也就是步長為：36÷9=4，獵狗的步長為：36÷4=9。所以兔子和狗的步長之比為4：9，所以可以得到速度之比為（8×4）：（5×9）=32：45。

“這是獵狗追兔問題，老爸，你的小心思可都讓我猜中了。”我轉頭對老爸說。

老爸也哈哈大笑起來，說：“沒錯，這就是獵狗追兔的解題關鍵——將行程單位統一。看來你早有研究，學得不錯嘛！”

“過情人節嘍，過情人節嘍。”8歲的小弟何疏文不知道怎么忽然興奮起來，蹦蹦跳跳地滿屋子瘋跑。

我忍不住調侃道：“情人節是大人們過的節日，你個小屁孩興奮個什么勁？”

小弟一聽，立刻撇起嘴大哭起來，又是打滾又是狼嚎……把老媽給招了來。“何疏雨！你是不是又欺負弟弟了？”老媽一邊呵斥我，一邊安慰起弟弟來。

“天地良心。”我急忙大呼冤枉。正要辯解，卻聽見老爸在門口喊道：“快點，她三姑等咱們呢。”

“趕緊把你弟弟哄好，要不然我饒不了你。”老媽老爸急著要去接來串門的姑姑，匆匆丟下句話就出了門。

老爸老媽一出門，弟弟立刻停止了哭聲，跟我談起條件來。“姐姐要是幫我解道數學題，我就不鬧了。”

“嘿！臭小子敢威脅我。”我剛要伸手，就看弟弟立刻眼淚汪汪，馬上就要流下來。

“好了，好了，我輸了。”我無奈地說，“什么數學題，說吧！”

獵狗前面26步遠有一只野兔，獵狗追之。野兔跑8步的時間狗跑5步，野兔跑9步的距離等于狗跑4步的距離。問：野兔跑多少步后被獵狗抓獲？此時獵狗跑了多少步？

獵狗追兔？這題對8歲的弟弟來說確實有些難。就算是我也要細細思索一番呢。我細細分析起來：

“獵狗前面26步……”顯然指的是獵狗的26步。

“兔跑8步的時間……”和“兔跑9步的距離……”，那么第一件事就是要做統一單位，8與9的最小公倍數是72，所以可以統一在“兔跑72步”這個情況下考慮。

野兔跑72步的時間狗跑45步，野兔跑72步的距離等于獵狗跑32步距離，所以在野兔跑72步的時間里，獵狗比野兔多跑了45-32=13（步）的路程，這個13步是獵狗的13步。

由此代入公式，問題的答案就是：

要追上獵狗跑的26步，野兔需要跑：

72×（26÷13）=144（步）;

此時獵狗跑了5×（144÷8）=90（步）。

“我懂嘍，謝謝姐姐！”我話音剛落，鬼小弟已經跑得沒了影子。唉，這個讓人頭痛不已的小弟呀！

早上起來，我不經意間看了眼日歷，咦？為什么2月份只有29天呢？其他月份不是30天，唯獨二月天數最少，不是28天，就是29天？

我帶著疑問找到姐姐。姐姐眼珠骨碌碌地轉了半天，說：“這個問題嘛，我原是知道的。”“那還不快快告訴我。”我焦急地問道。

“但我偏要賣個關子。”姐姐說，“明天就要開學了，我有道數學題怎么也解不出來，你要是能幫我解出來，我就告訴你。”

我這個姐姐呀，真是叫人又恨又愛。形勢所迫，我只好無奈地說：“什么題，讓我先看看。”

姐姐立刻興奮起來，就是這一道：

貓跑5步的路程與狗跑3步的路程相同;貓跑7步的路程與兔跑5步的路程相同;而貓跑3步的時間與狗跑5步的時間相同;貓跑5步的時間與兔跑7步的時間相同，貓、狗、兔沿著周長為300米的圓形跑道，同時同向同地出發。問當它們出發后第一次相遇時各跑了多少路程？

“這不就是‘獵狗追兔問題嘛！”我心里暗想，“只不過又加入了貓……要先捋清題中已知條件！”我嘴上念叨著，找來紙筆，寫道：

相同路程內，貓跑5步等于狗跑3步……假設距離為15的話，貓的步長為：15÷5=3，狗的步長為：15÷3=5。所以，貓和狗的步長比為3：5。

相同時間內，貓跑3步，狗跑5步……也就是貓腳落地次數為3，獵狗腳落地次數為5。所以可以得到貓和狗的步頻之比為3：5。

所以，貓和狗的速度比為（3×3）：（5×5）=9：25。

同理，貓與兔的速度之比為：25：49。

設單位時間內貓跑1米，則狗跑? ? ? ?米，兔跑? ? ? ? 米。

狗追上貓一圈需? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?單位時間;

兔追上貓一圈需? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 單位時間;

貓、狗、兔再次相遇的時間，應既是? ? ? ? 的整數倍，又是? ? ? ? ? 的整數倍;

與? ? ? ? ? 的最小公倍數等于兩個分數中分子的最小公倍數除以分母的最大公約數，即

[? ? ? ? ? ，? ? ? ? ? ?]=? ? ? ? ? ? ? ? ? ?=? ? ? ? ? ? ? =8437.5。

也就是經過8437.5個單位時間，貓、狗、兔第一次相遇。

所以，貓跑了8437.5米;狗跑了8437.5×

=23437.5米;兔跑了8437.5×? ? ? ? ? =

16537.5米。

姐姐看了我的解題方法頻頻點頭，說：“不愧是數學小天才呢！看你這么聰明的份上，就給你講講2月份少一兩天的原因吧！”

為什么2月份只有29天？

我們現在使用的公歷，是古羅馬帝國時期完善成形的。地球繞太陽運行1周的時間是365.2422天，為1年，1年分12個月。

羅馬大帝愷撒規定：每年12個月，一、三、五、七、十、十二為大月，每月31天;其他月份定為小月，每月30天，這樣，大小各六個月，很容易讓人記住。但照這樣規定，一年就不是365天，而是366天了，因此得找出一個月扣去一天。那個時候被判處死刑的犯人都在2月份處死，人們都希望2月能快點過去。于是，就把2月扣去了一天，這樣，2月就只剩下29天了。

再后來，一個叫奧古斯特的人做了羅馬皇帝。奧古斯特是八月份生的，八月卻是小月，他就荒唐地把八月也定為大月，改為31天。而八月多出的這一天仍然從二月份扣除，這樣，二月只剩下28天了，只是每過4年，也就是閏年，二月才是29天，這就是二月份天數少的來歷。