含運動分岔閉鏈的多運動模式并聯機構

王 艷， 許 勇， 董 飛， 張強強， 趙傳森

(上海工程技術大學 機械與汽車工程學院， 上海 201620)

運動分岔機構是指通過奇異位形前后，自由度特性(自由度數目或類型)及相應位形發生改變的機構[1]。運動分岔機構是新興的可重構機構，可作為變自由度可伸展機構、多軸聯動多面加工裝備和多步態靈活移動裝置的運動執行機構，無疑具有很高的研究價值和廣闊應用前景[ 2-3]。課題組將機構的特定自由度及其相應位形稱為機構的運動模式。

奇異位形是運動分岔機構不同運動模式間的瞬時轉換位形[4]。通過在奇異位形中引入新的驅動副，運動分岔機構可離開瞬時奇異位形，切換為連續運動模式[5]。對運動分岔機構來說，奇異位形往往是自由度切換位形，而非需要避免的失控位置[6]。

課題組將運動分岔特性引入到并聯機構中，提出了新構型的運動分岔并聯機構。課題組認為，分岔機構在通過瞬時奇異位形前后自由度發生改變的根源，在于分岔機構支鏈中約束特性(約束螺旋數量或軸線方向)的改變，因而機構支鏈中必定存在著多個線性相關的約束螺旋，這通常由通過切換驅動副從而實現過約束的分岔閉鏈來實現[7]。所以可認為分岔機構的變自由度特性來自于分岔閉鏈。

目前研究者們已經提出了一些運動分岔機構：LI等提出了具有不同schoenflies運動分岔特性的并聯機構[8];Galletti等提出了許多具有運動分岔特性的機構[9];ZENG等提出了一款4自由度混聯分岔機構[10]；LEE等提出一種廣義運動分岔機構是運動限定6R機構[11]58；葉偉等利用單環閉鏈的約束奇異特性提出一系列可重構并聯機構[12-14]。

課題組提出了一種URRC(萬向節-轉動副-轉動副-圓柱副)構型的運動分岔閉鏈，具有單自由度整體空間連續轉動或者單自由度平面連續運動2種運動模式。以此運動分岔閉鏈為核心單元，構建了具有5自由度和6自由度運動模式的混聯支鏈，及具有3轉3移、3轉2移、3轉1移和2轉1移共4種運動模式的并聯機構。基于螺旋理論[15]對分岔閉鏈、混聯支鏈及并聯機構的自由度進行了分析，驗證了多運動模式分岔閉鏈、支鏈和并聯機構構型設計的合理性。

1 運動分岔閉鏈自由度分析

1.1 運動分岔閉鏈奇異位形下瞬時自由度分析

課題組提出的具有運動分岔特性的閉鏈如圖1所示，閉鏈的構型為URRC(萬向節-轉動副-轉動副-圓柱副)。LEE[11]60所提出的運動限定6R機構由2個轉動副和2個萬向節連接的4桿組成，該機構可以執行平面4桿運動和單軸轉動運動。課題組提出的閉鏈用圓柱副代替了LEE[11]61所述的一個萬向節，可以執行平面曲柄滑塊連續運動和整體空間連續轉動。

機架與構件AS在A點通過圓柱副相連，構件AB與構件AS在A點以轉動副連接，構件AB與構件BG在B點以轉動副連接，機架與構件BG在G點通過萬向節相連，其中構件BG長度為a，AG長度為b，其中A,B,G為運動副形心。

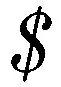
選取圖1中構件AS為輸出構件，該輸出構件右端通過支鏈1(包含轉動螺旋SA1和移動螺旋SA2)，左端通過支鏈2(包含轉動螺旋SA3,SB,SG1和SG2)與機架連接。則支鏈1和支鏈2的運動螺旋分別為:

(1)

(2)

對式(1)和式(2)取反螺旋可得支鏈1和2的約束螺旋為：

(3)

(4)

由(3)和式(4)可得2條支鏈的在奇異位形下的公共約束為：

(5)

因此，奇異位形下的公共約束數λ=2，機構的階數d=6-λ=4。奇異位形不存在并聯冗余約束，由修正的G-K公式可得在奇異位形下閉鏈瞬時自由度為：

(6)

式中：M表示機構的自由度；n表示包含機架的構件數；g表示運動副的數；fi為第i個運動副的自由度數;v代表并聯冗余約束數。

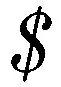
SB·SG1=sinα·sinβ=0。

(7)

由式(7)看出，α=0且β=0時即為奇異位形；α=0或β=0時為一般位形，且α=0和β=0不能同時存在。

1.2 運動分岔閉鏈模式Ⅰ自由度分析

(8)

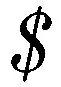
(9)

(10)

由式(9)和(10)可得該閉鏈公共約束為0，機構的階d=6。2條支鏈共有6個約束螺旋線性相關其秩為5，存在并聯冗余約束v=1。在此位形下閉鏈的自由度數為:

M=6(4-4-1)+6+1=1。

(11)

對式(14)和(15)的約束螺旋系取反螺旋可得構件AS的運動螺旋為

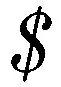
(12)

由式(12)可見,當β=0，α為任意角時，構件AS的自由度為1，運動為繞x軸的連續運動。如圖2(b)所示，此時閉鏈整體被剛化稱為單自由度整體空間轉動連續運動模式。

1.3 運動分岔閉鏈模式Ⅱ自由度分析

(13)

式中：(xA,yA,zA)表示A點坐標。

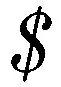
(14)

(15)

由式(14)和(15)可得該閉鏈公共約束為0，機構的階d=6。2條支鏈共有6個約束螺旋線性相關其秩為5，存在并聯冗余約束v=1。在此位形下閉鏈的自由度數為

M=6(4-4-1)+6+1=1。

(16)

對式(9)和(10)的約束螺旋系取反螺旋可得構件AS的運動螺旋為:

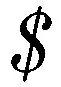
(17)

由式(17)可見，當α=0，β為任意角時，構件a的自由度為1，運動為沿x軸的平移運動。如圖3(b)所示，此時整個機構稱為單自由度平面運動連續運動模式。

2 運動分岔混聯支鏈自由度分析

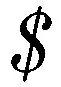
2.1 混聯支鏈5自由度模式

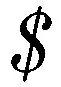
(18)

對式(18)運動螺旋求其反螺旋，可得混聯支鏈的約束螺旋為：

(19)

式中：(xD,yD,zD)表示D點坐標;(xE,yE,zE)表示E點坐標;(xF,yF,zF)表示F點坐標。

如用該混聯支鏈組裝得到并聯機構，由式(19)表明，模式Ⅰ時混聯支鏈對動平臺施加一個約束力線矢，該力線矢與固定坐標系x方向相同且通過球面副所在的F點，此時混聯支鏈為5自由度模式。

2.2 混聯支鏈6自由度模式

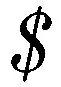
(20)

由式(20)可見，模式Ⅱ時混聯支鏈的運動螺旋秩為6，則混聯支鏈無約束作用于動平臺，混聯支鏈模式為6自由度模式。

3 運動分岔并聯機構運動模式自由度分析

如圖6所示，利用3條對稱布置的URRC-RRS混聯支鏈組裝為運動分岔并聯機構。混聯支鏈的運動分岔閉鏈與定平臺相連，混聯支鏈的球面副與動平臺相連。建立定坐標系o0-x0y0z0于定平臺的幾何中心，x0方向與混聯支鏈1的機架方向平行，y0垂直于定平臺，z0由右手定則確定。建立動坐標系o1-x1y1z1在動平臺的運動中心，其方向與定坐標系一致。

3.1 3轉3移運動模式

若并聯機構的3條混聯支鏈都工作在6自由度模式，此時將無約束作用于動平臺。該運動模式下并聯機構的自由度為6，可實現圖7所示的3轉3移運動模式。

3.2 3轉2移運動模式

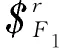
(21)

式中：P1,Q1和R1為常數。

由式(21)可知，該約束力線矢作用于混聯支鏈1球面副F1上且與動平臺x1正方向平行，它約束了運動平臺沿x1方向的移動。在該模式下可實現圖8(b)3轉2移運動模式。

3.3 3轉1移運動模式

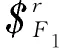
(22)

式中：Pi,Qi和Ri(i=1,2)為常數。

3.4 2轉1移運動模式

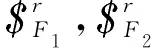
(23)

式中：Pi,Qi和Ri(i=1,2,3)為常數。

由式(23)和圖10(b)可知，3個約束力線矢共面、不平行也不匯交一點，它們約束了動平臺沿x1和z1的移動及繞y1的轉動。可見在該模式下可實現2轉1移運動模式。

4 支鏈輸入副選取合理性分析

根據輸入選取原理[17]，鎖死所有輸入運動副后，若動平臺約束螺旋的秩為6，則動平臺將失去全部6個自由度，選取合理。鎖死奇異位形下每一支鏈的2個輸入運動副，每一支鏈的機構被剛化，如將混聯支鏈的定坐標系o-xyz平移至轉動副D的形心，此時混聯支鏈的運動螺旋為:

(24)

對式(24)取反螺旋得混聯支鏈的約束螺旋為:

(25)

式中：Δy=yF-yE;Δz=zF-zE。

由式(25)可見，剛化輸入副后，動平臺將受到每條混聯支鏈2個約束力線矢的作用。一個約束力線矢與定坐標系x軸平行；另一約束力矢平行于構件EF。

在定坐標系下，并聯機構的約束螺旋為:

(26)

式中：d為定平臺中心o0到等邊三角形各邊的距離。

由式(26)可見，在定坐標系下，動平臺約束螺旋的秩為6。如輸入副被剛化，并聯機構的動平臺將失去6個自由度，所以輸入方案選取是合理的。

5 結論

1) 課題組提出一種構型為URRC運動分岔閉鏈，閉鏈具有2自由度奇異位形下的瞬時運動，一般位形下有單自由度整體空間連續轉動或者單自由度平面連續運動2種互斥運動模式。

2) 將運動分岔閉鏈與5自由度RRS開鏈串聯得到一種混聯支鏈。該混聯支鏈具備2種獨立運動模式，輸入副不同可使得混聯支鏈在5自由度模式和6自由度模式切換。

3) 利用3條對稱布置的URRC-RRS混聯支鏈得到運動分岔并聯機構。混聯支鏈模式選取不同，運動分岔并聯機構具有3轉3移、3轉2移、3轉1移和2轉1移4種不同運動模式。