改進果蠅優化LSSVM超聲波萃取產物濃度軟測量

廖建慶，王涵，王咸鵬

改進果蠅優化LSSVM超聲波萃取產物濃度軟測量

廖建慶1，王涵1，王咸鵬2

(1. 宜春學院物理科學與工程技術學院，江西宜春 336000；2. 海南大學南海海洋資源利用國家重點實驗室，海南海口 570228)

針對超聲波天然產物萃取過程中產物濃度難以在線檢測的問題，提出了一種改進果蠅優化最小二乘支持向量機(Least Squares Support Vector Machine, LSSVM)的超聲波萃取產物濃度軟測量建模方法。首先將混沌優化與迭代步長動態調節方法相融合，提出了一種混沌動態步長改進果蠅優化算法(Chaos Dynamic Step Fluit Fly Optimization Algorithm, CDSFOA)，該算法引入動態調節因子對步長動態更新，并利用混沌優化實現各變量之間映射等操作，能夠有效提高果蠅優化算法的收斂精度和收斂速度，然后利用CDSFOA對LSSVM進行參數尋優，構建最優CDSFOA-LSSVM軟測量模型，最后利用超聲波斛皮素萃取實驗數據進行驗證。結果表明，提出的模型不僅有較好的學習和泛化能力，而且具有良好的預測精度，可為超聲波天然產物萃取工藝優化提供理論指導。

超聲波；萃取；最小二乘支持向量機；軟測量

0 引言

在超聲波天然產物萃取領域，通常需要對萃取產物溶液濃度進行實時監測，以便及時了解和掌握萃取過程的工作狀況和參數變化情況。產物溶液濃度作為萃取過程控制的關鍵參數，目前主要通過間斷取樣、實驗室滴定的方法獲得，這樣不可避免地存在一定的滯后性, 不能及時調整不合理的萃取參數和狀態，而且有時對腐蝕性強的液體檢測還存在一定的困難[1]。因此，建立準確、可靠的超聲波萃取過程產物濃度的軟測量模型，對提高超聲波萃取質量、提升超聲波天然產物萃取過程的自控水平具有重要意義。

針對諸多化學工業過程的優化問題，國內外學者已提出了大量基于數據驅動的軟測量方法，由于最小二乘支持向量機(Least Squares Support Vector Machine, LSSVM)采用等式約束與平方和的誤差成本函數，只要求解一個線性方程組，這樣使得運算效率得到極大提高[2]。因此，在發醇過程建模[3]、超聲波萃取過程建模[4]、熔解指數預測[5]等非線性化學工業建模領域得到了廣泛應用。研究表明，最小二乘支持向量機的精度和泛化能力主要受核函數和懲罰系統這兩個參數的影響，目前已有許多國內外研究者采用果蠅優化算法(Fruit Fly Optimization Algorithm, FOA)[6]及其改進算法對最小二乘支持向量機的兩個主要參數進行優化，并取得了較好效果。

果蠅優化算法是臺灣學者潘文超首次提出的一種群智能算法[6]。該算法是一種基于果蠅覓食行為而推演出的全局優化算法，已成功應用于(Proportion Integration Differentiation, PID)控制參數優化[7]、支持向量機參數優化[8]、多目標優化[9]等領域。相較于其他群智能算法，果蠅優化算法具有結構和計算簡單、運行時間短和可調參數少等優點[6]。當然，由于算法自身的特點，果蠅優化算法與其他智能算法一樣，也存在收斂速度慢、精度低等問題。對此，Liao等[4]在果蠅優化算法的基礎上做了改進，同時對LSSVM參數尋優，得到了超聲波萃取過程軟測量模型。但由于算法種群單一且缺乏遍歷性，使得模型存在精度不高且運算速度較慢等問題。

本文提出了一種混沌動態步長改進果蠅優化算法。一方面，通過利用混沌特性來提高果蠅種群的多樣性和搜索的遍歷性，引入混沌擾動變量來提高算法的持續搜索能力；另一方面，通過引入步長動態調節因子對果蠅搜索步長進行隨機動態調節，使得算法的收斂速度得到進一步提高，改進算法能有效地提高種群的多樣性和搜索的遍歷性，進而提高算法精度，避免陷入局部最優。然后利用該改進果蠅優化算法對LSSVM參數進行尋優，并將該建模方法應用于超聲波天然產物(衛矛莖干)萃取斛皮素溶液濃度的軟測量中。

1 最小二乘支持向量機

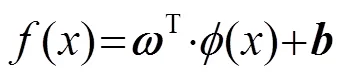
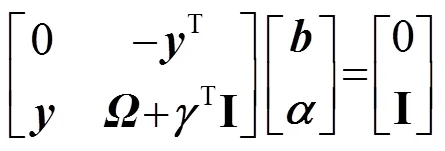
求解式(4)，可得最小二乘支持向量機的輸出為

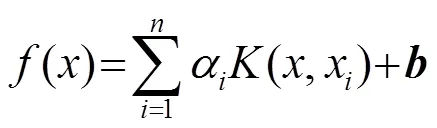
2 果蠅優化算法的改進

2.1 初始果蠅優化算法

初始果蠅優化算法步驟如下：

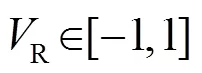
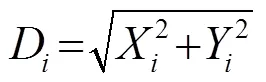
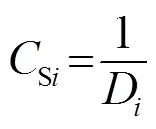
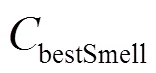
(6) 根據記錄的最佳果蠅序號和最佳的果蠅位置(最優個體)，此時所有果蠅個體利用視覺向最佳位置飛去；

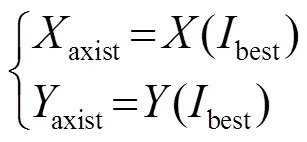
(7) 最后進行迭代過程，重復步驟(2)～(5)，在尋優過程中判斷當前迭代的最佳味道濃度是否優于上一迭代的最佳味道濃度，同時，判斷當前迭代次數是否小于最大迭代次數；若是則執行步驟(6)，否則結束。

2.2 步長調節策略

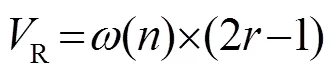
果蠅個體利用嗅覺搜尋食物的隨機方向與距離式(6)調整為

隨迭代次數的動態變化見圖1。結合式(13)～(15)和圖1可見，在算法迭代初期，隨迭代次數的增加衰減較慢，即保持一個較大的步長尋優，可以有效地避免算法過早陷入局部最優。到了迭代后期，隨迭代次數的增加而衰減到一個很小的值，使得算法在后期的收斂速度加快，從能克服果蠅算法在尋優后期收斂速度慢、易陷入局部最優等缺點。

2.3 混沌優化

混沌優化[11]是一種利用混沌運動特性進行優化搜索方法，由于混沌變量映射通常是由Logistic方程得到，而Logistic映射是混沌系統中最著名及應用最多的系統模型之一，因此本文引入Logistic 映射，其數學模型為

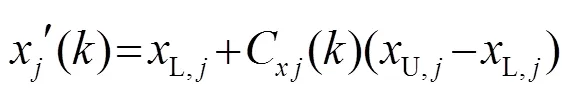
2.4 算法驗證

由表2可見，與PSO、BA、FOA算法相比， CDSFOA算法對各測試函數都能找到或更接近理論的最優值，即求解得到的最優值、最差值、優化均值和標準方差均優于POS、BA和FOA算法；另外在搜索時間方面，CDSFOA算法相比PSO和BA 兩種算法所需時間都要短，但也發現CDSFOA算法相比FOA算法所需時間稍長，可能的原因為CDSFOA算法對果蠅群體做了動態步長的調節操作和引入了混沌擾動操作，從而增加了運算時間。同時也發現，改進算法在尋優精度方面要遠優于FOA算法，表明本算法具有更高的精度和更好的穩定性。

表1 測試函數

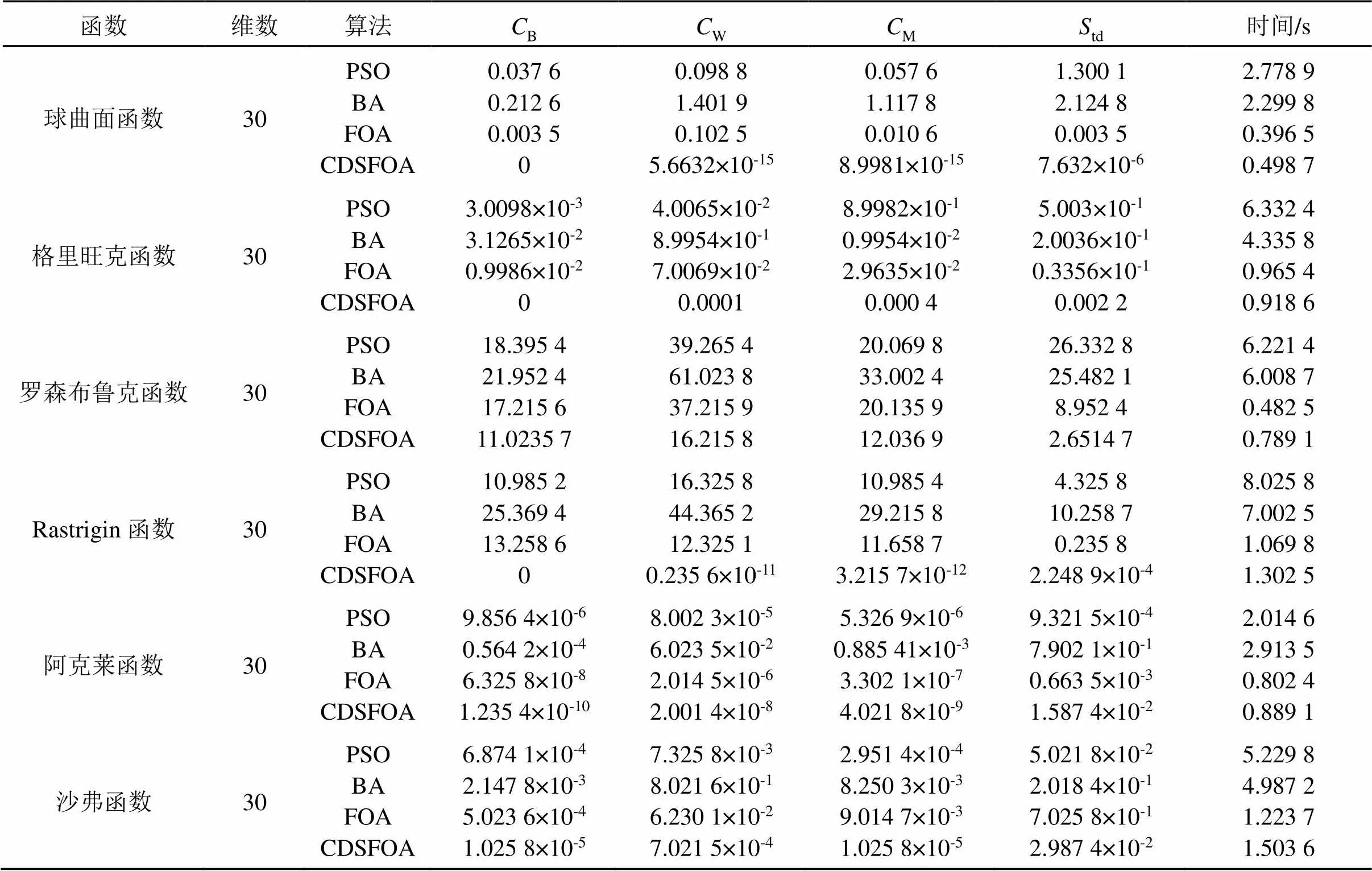
表2 各算法的性能比較

3 CDSFOA優化LSSVM軟測量模型

3.1 基于CDSFOA算法的LSSVM模型參數優化

(1) 參數初始化；

3.2 CDSFOA-LSSVM建模步驟

基于CDSFOA-LSSVM的超聲波提取過程建模流程如圖2所示，其建模實現步驟如下：

(1) 確定模型的輸入變量和輸出變量，同時對樣本預處理；

(3) 構建模型的核矩陣；

(5) 求解偏置項的值、最優向量和支持向量，構造CDSFOA-LSSVM的輸出模型；

(6) 利用CDSFOA-LSSVM模型對超聲波提取過程進行訓練和預測。

4 斛皮素濃度預測模型

超聲波天然產物萃取槽簡易模型如圖3所示。為了構建超聲波天然物提取過程的軟測量預測模文以天然產物——衛矛莖干為萃取對象，通過主成分分析法確定萃取溫度、萃取時間、超聲頻率、超聲功率、溶劑濃度和液料比等6個萃取變量作為模型的輸入，將萃取產物斛皮素溶液濃度作為模型的輸出。以超聲波衛矛莖干萃取過程實驗數據作為建模數據樣本，樣本隨機取自不同的實驗批次。

圖2 基于CDSFOA-LSSVM的超聲波提取過程建模流程圖

圖3 超聲波萃取槽示意圖

依據上述建模方法，利用CDSFOA-LSSVM的超聲波萃取過程的建模步驟，首先，對樣本做歸一化預處理，然后將樣本分為訓練樣本集、驗證樣本集和推廣樣本集。然后利用訓練樣本集訓練LSSVM模型，接著再利用CDSFOA對LSSVM兩個參數進行尋優，得到優化后的CDSFOA-LSSVM軟測量模型，最后利用驗證樣本集對軟測量模型預測效果進行檢驗。預測誤差如表3所示。

表3 模型對驗證樣本集的預測誤差

由表3可見，改進果蠅優化后的LSSVM模型相對初始LSSVM模型的平均絕對誤差(MA)、平均相對誤差(MR)、均方根誤差(RMS)和標準差(td)分別減少了0.015 4、1.14%、0.034 4和0.034 9，說明CDSFOA-LSSVM軟測量模型對驗證樣本集的預測誤差明顯小于初始LSSVM，而FOA算法優化的LSSVM模型介于中間。

為了進一步驗證所提模型的推廣性能，初始LSSVM、FOA-LSSVM和CDSFOA-LSSVM預測模型對推廣樣本集的預測誤差結果如表4所示。

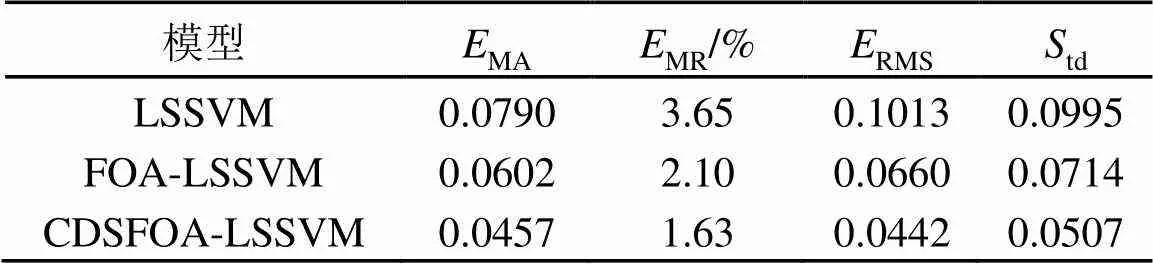
表4 模型對推廣樣本集的預測誤差

從表4中四個誤差指標可見，優化后的LSSVM模型比初始LSSVM模型得到的預測結果更接近真實值，而改進后的果蠅優化算法CDSFOA相比未改進的果蠅優化算法FOA優化效果更好。其中，CDSFOA-LSSVM的MA相對初始LSSVM的MA減少了0.033 3，MR減少了2.02%，RMS減少了0.057 1，td減少了0.0488。

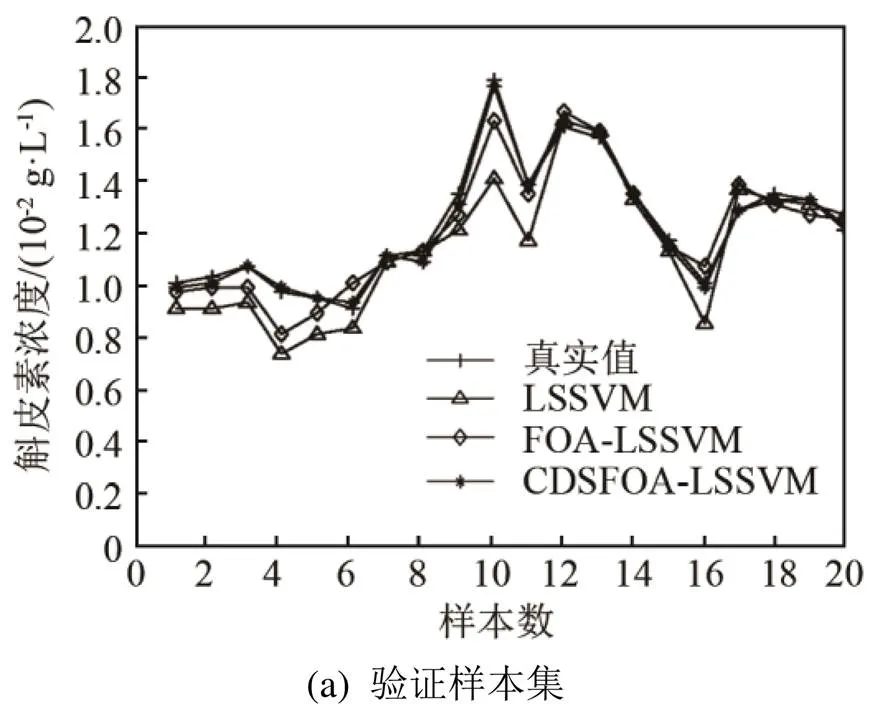
優化前后LSSVM預測模型對驗證樣本和推廣樣本的預測跟蹤結果如圖4所示。由圖4可以看出，改進的果蠅優化LSSVM預測模型相比未改進的果蠅優化LSSVM以及初始LSSVM預測模型的跟蹤性能得到了明顯提高，更加接近真實值。另外，優化后的LSSVM模型的泛化能力比初始LSSVM更好，如圖4(b)所示。

5 結論

(1) 在初始果蠅算法的基礎上，引入步長動態調節因子和混沌優化算法，提出了一種性能更加優越的改進果蠅優化算法(CDSFOA)。

(2) 為驗證模型的有效性，通過6個測試函數的仿真實驗，表明該算法相比其他對比算法在收斂精度和速度方面有明顯的優勢。

(3) 通過超聲波萃取斛皮素濃度過程建模實例，比較初始LSSVM、FOA優化的LSSVM以及CDSFOA優化的LSSVM預測模型，表明CDSFOA優化算法提高了模型的預測精度和泛化能力。

[1] 劉鎮清. 化工生產液濃度的超聲波在線檢測[J]. 現代化工, 1995, 15(8): 43-44.

LIU Zhenqing. Ultrasonic online detection of chemical production liquid concentration[J]. Modern Chemical Industry, 1995, 15(8): 43-44.

[2] 石洋, 胡長青. 基于粒子群最小二乘支持向量機的前視聲吶目標識別[J]. 聲學技術, 2018, 37(2): 122-128.

SHI Yang, HU Changqing. Forward-looking sonar target recognition based on particle swarm and least squares support vector machine[J]. Technical Acoustics, 2018, 37(2): 122-128.

[3] NIU D P, ZHANG L, WANG F L. Modeling and parameter updating for nosiheptide fed-batch fermentation process[J]. Industrial & Engineering Chemistry Research, 2016, 55(30): 8395-8402.

[4] LIAO J Q, QU B D, ZHENG N. Effects of process parameters on the extraction of quercetin and rutin from the stalks of euonymus alatus (thumb.) sieb and predictive model based on least squares support vector machine optimized by an improved fruit fly optimization algorithm[J]. Applied Sciences, 2016, 6(11): 340-359.

[5] WANG W C, LIU X G. Melt index prediction by least squares support vector machines with an adaptive mutation fruit fly optimization algorithm[J]. Chemometrics and Intelligent Laboratory Systems, 2015, 141: 79-87.

[6] PAN W T. A new fruit fly optimization algorithm: taking the financial distress model as an example[J]. Knowledge-Based Systems, 2012, 26: 69-74.

[7] ZHANG X Y, CHEN G, JIA S M. Parameters optimization of PID controller based on improved fruit fly optimization algorithm[C]//International Conference on Swarm Intelligence. Springer, Cham, 2018: 421-431.

[8] ZHANG Q T, FANG L Q, MA L L, et al. Research on parameters optimization of SVM based on improved fruit fly optimization algorithm[J]. International Journal of Computer Theory and Engineering, 2016, 8(6): 500-505.

[9] RIZK-ALLAH R M, EL-SEHIEMY R A, DEB S, et al. A novel fruit fly framework for multi-objective shape design of tubular linear synchronous motor[J]. The Journal of Supercomputing, 2017, 73(3): 1235-1256.

[10] YU Y C, LI Y, LI J C, et al. Self-adaptive step fruit fly algorithm optimized support vector regression model for dynamic response prediction of magnetorheological elastomer base isolator[J]. Neurocomputing, 2016, 211: 41-52.

[11] 廖建慶, 王涵, 王咸鵬. 混沌動態步長果蠅優化算法[J]. 傳感器與微系統, 2019, 38(8): 139-142.

LIAO Jianqing, WANG Han, WANG Xianoeng. Health state assessment of a rolling bearing based on CFOA-MKHSVM method[J]. Chinese Journal of Scientific Instrument, 2019, 38(8): 139-142.

[12] VAIDYANATHAN S. Chaos in neurons and adaptive control of Birkhoff-Shaw strange chaotic attractor [J]. International Journal of PharmTech Research, 2015, 8(5): 956-963.

[13] YUAN X F, DAI X S, WU L H. A mutative-scale pseudo-parallel chaos optimization algorithm[J]. Soft Computing, 2015, 19(5): 1215- 1227.

Soft measurement of ultrasonic extracted product concentration by LSSVM of improved fruit fly optimization algorithm

LIAO Jianqing1, WANG Han1, WANG Xianpeng2

(1. College of Physical Science and Engineering, Yichun University, Yichun 336000, Jiangxi, China; 2. State Key Laboratory of Marine Resources Utilization of the South China Sea, Hainan University, Haikou 570228, Hainan, China)

Aiming at the problem that the product concentration in ultrasonic natural product extraction is difficult to detect online, a soft measurement method using the least squares support vector machine (LSSVM), which is optimized by an improved fruit fly optimization algorithm (FOA), is proposed. Firstly, the improved FOA with chaotic dynamic step size (named as CDS-FOA) is obtained by combing chaos optimization and iterative step-size dynamic adjustment. This algorithm introduces the dynamic adjustment factor to update the step size dynamically, and uses chaos optimization to realize the mapping between different variables, which can effectively improve the convergence precision and convergence speed of the FOA. Then, the CDS-FOA is used to optimize the parameters of LSSVM to construct the optimal CDSFOA-LSSVM soft measurement model. Finally, the experimental data from ultrasonic quercetin extraction are used to verify the effectiveness. Results show that the proposed model not only has better learning and generalization ability, but also has good prediction accuracy, which can provide guidance for the optimization of ultrasonic natural product extraction processes.

ultrasonic; extraction; least squares support vector machine (LSSVM); soft measurement

O426

A

1000-3630(2020)-02-0169-07

10.16300/j.cnki.1000-3630.2020.02.008

2019-01-12;

2019-03-16

國家自然科學基金項目(61701144)、江西省教育廳科技項目(GJJ170894)；江西省高等學校教改課題(JXJG-18-15-5)

廖建慶(1977－), 男, 江西吉安人, 博士, 副教授, 研究方向為超聲波天然物提取過程建模與優化。

廖建慶,E-mail: jndxljqbs@126.com