紅外高光譜干涉儀輻射定標誤差敏感性因子的仿真分析

陸其峰，徐一樹，吳春強，漆成莉

(1. 中國氣象科學研究院 災害天氣國家重點實驗室，北京 100081；2. 國家衛星氣象中心 中國遙感衛星輻射測量與定標重點開放實驗室，北京 100081)

1 引 言

紅外高光譜干涉儀是實現高光譜分辨率紅外大氣探測的重要儀器，具有高光通量、多通道的優點[1]。歐洲和美國分別于2006年和2011年在新一代極軌衛星上搭載了一臺干涉式紅外高光譜探測儀，分別為IASI[2-3](Infrared Atmospheric Sounding Interferometer)和CrIS[4-6](the Cross-track Infrared Sounder) 。我國也在2016年新一代靜止氣象衛星(風云四號)上搭載了全球首臺靜止軌道干涉式紅外高光譜探測儀[7-8](Geosynchronous Interferometric Infrared Sounder,GIIRS)。2017年發射的風云三號04星上也搭載了一臺干涉式紅外高光譜探測儀[9-10](High-spectral Infrared Atmospheric Sounder,HIRAS)。星載紅外高光譜干涉儀的廣泛應用極大地推動了高光譜大氣探測技術的發展，其探測資料對于數值天氣預報的改進、氣候變化和預測的研究、大氣溫濕廓線和氣體成分的反演有著極其重要的意義[11]。

為了能夠得到較精確的高光譜信息，需要通過定標過程來校正干涉儀所觀測到的數據，包括光譜定標[12]和輻射定標。輻射定標主要是利用兩個校準目標源(內黑體暖目標和冷空冷目標)來去除儀器自發射和儀器響應率的影響，校準場景目標的輻射能量。研究表明，儀器的非線性效應、偏振效應等會對觀測的干涉或光譜信息產生一定的影響，需要在輻射定標之前進行訂正處理。

盡管目前輻射定標模型已經建立得比較完備，并廣泛應用在各種紅外高光譜干涉儀的輻射定標過程中[3,5,10,13]。但是，不同干涉儀的特征不同，且在軌后隨著時間的推移儀器產生的參數擾動也不同，這些儀器參數及其變化會對輻射定標精度造成一定的影響。因此，針對不同儀器細致分析輻射定標參數對定標精度的影響非常重要。國內外的專家學者針對紅外高光譜干涉儀輻射定標過程中某些儀器參數及其擾動對輻射定標精度的影響開展了研究。Tobin等基于發射前CrIS儀器測試的定標參數的不確定度來估計輻射定標誤差，結果表明，對于溫度高于250 K的黑體目標，定標亮溫不確定度估計值低于0.2 K，其中內黑體溫度、內黑體反射的輻射項和探測器的非線性參數的擾動起主要作用[14]。楊敏珠等針對AVS研究了二次項非線性對光譜的影響，并應用于AVS的輻射定標中，結果表明，目標的溫度越高，非線性影響越大，且非線性訂正后的定標輻射曲線擬合優度大約提高了0.3%[15]。

本文利用輻射定標模型，針對模型中的各儀器參數做敏感性實驗。根據實驗結果和理論分析，總結了定標輻射隨不同誤差敏感性因子擾動的變化特征。一方面給出了儀器設計時定標參數所需的控制范圍；另一方面結合地面真空試驗的實際觀測樣本，對輻射定標參數進行了最優估計，提高了定標精度。

2 輻射定標模型

參考目前國際上流行的輻射定標方案[16]，利用高、低溫兩個目標源來對場景目標進行輻射定標。其中，高溫目標為高發射率和高穩定性的黑體，而低溫目標在在軌運行階段為宇宙背景(深空)，在地面實驗階段為高發射率和高穩定性低溫黑體。由此，輻射定標方程可表示為：

(1)

其中：R和C分別為光譜輻射和原始光譜，下標LBB，ICT和ES分別表示低溫黑體、內黑體和場景目標，Re()表示取實部。圖1和圖2顯示了風云三號E星HIRAS儀器的光路圖和觀測目標掃描模型。目標輻射光進入干涉系統后出來的干涉光進入探測器得到原始干涉圖，再通過傅里葉變換即可得到原始光譜。而不同觀測目標的選擇則是通過不同的掃描角度來獲得不同目標的輻射光。由于儀器效應的存在，需要利用兩個黑體目標源來對場景目標進行輻射定標，得到的定標輻射則能較好地還原目標的輻射信息。

圖1 風云三號E星HIRAS儀器光路Fig.1 Optical path of FY-3E HIRAS

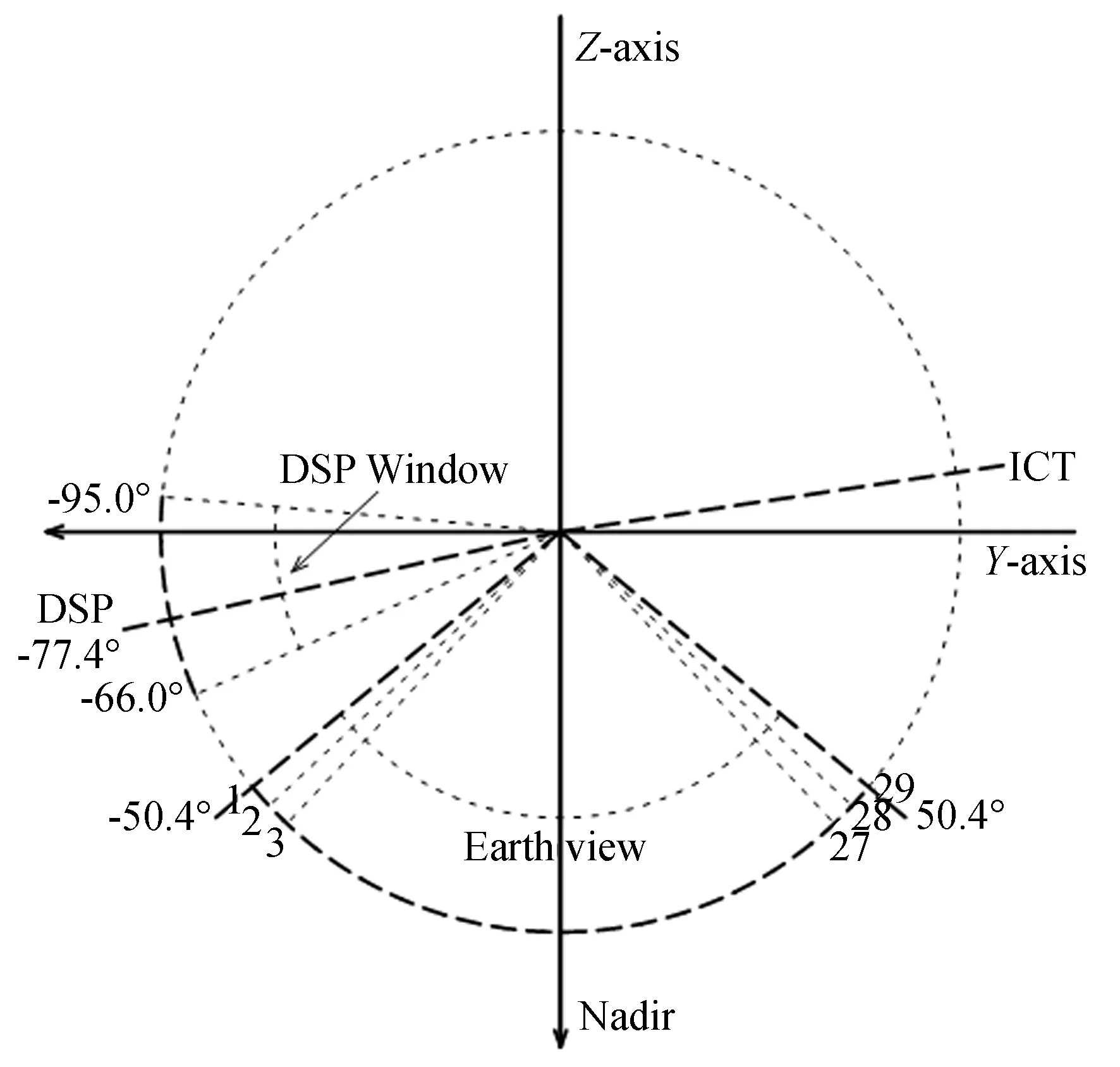
圖2 風云三號E星HIRAS儀器觀測目標掃描模型Fig.2 Target scanning model of FY-3E HIRAS

對于式(1)中的內黑體光譜輻射RICT和低溫黑體光譜輻射RLBB，通過下面兩式得到：

RICT=εICTB(TICT)+(1-εICT)ηICTB(TICT,env),

(2)

RLBB=εLBBB(TLBB)+(1-εLBB)ηLBBB(TLBB,env),

(3)

其中：ε表示黑體發射率，B表示普朗克函數，T表示溫度，η表示黑體所處環境的發射率。CLBB,CICT和CES分別為低溫黑體、內黑體和場景目標的原始光譜，它們受到儀器效應的影響，其中非線性效應是主要的不確定性因素。

受材料特性以及工藝水平的限制，實際制造的探測器具有非線性效應[17-18]，而且當入射光子通量越大時，產生的非線性效應更為顯著[19]。目前，在氣象應用領域，考慮探測器的二階非線性效應并加以訂正即可滿足天氣分析、數值天氣預報的應用要求。僅考慮探測器存在二階非線性效應時，其理想干涉圖IL與存在非線性的干涉圖I之間的關系如下：

(4)

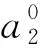
Cco=C(1+2a2V),

(5)

其中：Cco為非線性訂正后的原始光譜，C為觀測原始光譜，a2為非線性訂正系數，V為直流電壓。

由上面公式可知，黑體發射率、黑體環境溫度、非線性訂正系數、直流電壓等的測量誤差或估算誤差會直接影響最終的定標精度。

3 結果分析

3.1 內黑體

由于內黑體不是理想黑體(發射率不為1)，因此式(2)中實際內黑體輻射包含兩部分，一部分是內黑體自身發射的輻射，另一部分是內黑體反射的環境輻射。顯然，內黑體發射率以及內黑體與環境溫度差的測量精度會影響輻射定標精度。因此，本文以理想內黑體發射率的定標亮溫為參考，設計內黑體發射率和內黑體環境溫度的不確定性實驗來分析這兩者對輻射定標精度的影響。

3.1.1 內黑體發射率

根據在軌期間CrIS和HIRAS的溫度特征，控制內黑體與環境溫度差固定為6 K，考慮不同非理想內黑體發射率情況下的定標亮溫偏差。定標輻射偏差為定標輻射與場景目標的輻射的差，記為DR=RES-B(TES)。根據輻射定標模型，從理論上推導DR隨內黑體發射率εICT的變化，推導過程如下：

(6)

根據式(6)可以看出，定標輻射偏差與內黑體發射率呈線性關系，內黑體發射率越大，定標輻射偏差絕對值越小。新一代紅外遙感衛星儀器需要更高的絕對測量精度，其中輻射定標精度要優于0.1 K才能滿足氣候檢測的需求[20]。因此，要提高輻射定標精度，提高紅外高光譜干涉儀的內黑體發射率是一種必要的手段。根據上述推導，本文檢驗了輻射定標精度關于內黑體發射率的敏感性，結果如圖3所示。

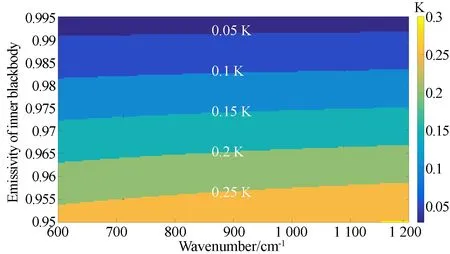
圖3 不同內黑體發射率與理想黑體發射率下定標亮溫偏差Fig.3 Brightness temperature differences between calibration with different emissivities of inner blackbody and ideal blackbody

從圖3可以看出，對于同一內黑體發射率來說，定標亮溫偏差隨波數的增大而緩慢增大。但這種變化的量級很小，且隨著內黑體發射率的增大而減小。另外，隨著內黑體發射率的增大，整個長波波數段的亮溫偏差都逐漸變小，梯度大約為ΔBT/ΔεICT=-0.029 K/0.005，且梯度幾乎不隨內黑體發射率的變化而改變。在本文建立的輻射定標模型中，只有將內黑體發射率提高到0.985以上，才能滿足0.1 K的輻射定標精度要求。

3.1.2 內黑體與環境溫度差

從式(6)可以發現，除了內黑體發射率，內黑體與環境溫度差也會影響輻射定標精度(假設內黑體環境的發射率為常數)。圖4顯示了在參考波數900 cm-1處，不同內黑體發射率下，定標亮溫偏差隨內黑體與環境溫度差的變化。

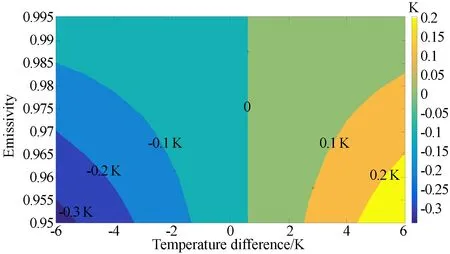
圖4 不同內黑體發射率條件下，參考波數900 cm-1處定標亮溫偏差隨內黑體與環境溫度差的變化Fig.4 Variations of brightness temperature difference with temperature differences between inner blackbody and environment for different emissivities of inner blackbody at reference wavenumber of 900 cm-1

由圖4所示，定標輻射對應的亮溫差為零時對應某一個內黑體與環境的溫度差，這是由內黑體環境發射率所決定的。根據式(6)，當ηICTB(TICT,env)=B(TICT)時，有定標輻射偏差為0，此時內黑體與環境的溫度差TICT,env-TICT即為圖4中亮溫差為0所對應的溫度差。在本文所建立的輻射定標模型中，這個參考溫度差與環境發射率有關，大約為0.6 K左右。同一內黑體發射率情況下，內黑體與環境溫度差越接近上述的參考溫度差，定標亮溫偏差越小，輻射定標精度越高。

3.2 低溫黑體

同樣地，一般情況下低溫黑體的發射率也不能達到理想情況(發射率為1)。因此，低溫黑體的輻射包含兩部分，一部分是低溫黑體的自發射輻射，另一部分是低溫黑體反射的環境輻射，如式(3)所示。由于低溫黑體環境溫度與低溫黑體溫度存在較大差異，因此只有控制低溫黑體的發射率來能獲得高輻射定標精度。

根據輻射定標模型，可以推導出定標輻射偏差DR隨低溫黑體發射率εLBB的變化，推導過程如下：

ηLBBB(TLBB,env)].

(7)

根據式(7)，可以看出定標輻射偏差與低溫黑體發射率呈線性關系，低溫黑體發射率越大，定標輻射偏差的絕對值越小。提高低溫黑體發射率，能有效地提高輻射定標精度。根據輻射定標模型，控制其他條件不變，討論不同低溫黑體發射率情況下定標亮溫偏差的變化，敏感性實驗結果如圖5所示。

圖5顯示對于同一低溫黑體發射率，定標亮溫偏差隨著波數的增大而緩慢減小，且這種變化隨著低溫黑體發射率的升高而減小。另一方面，隨著低溫黑體發射率的增大，整個長波波數段的定標亮溫偏差都逐漸減小，梯度大約為ΔBT/ΔεLBB=-0.028 7 K/0.005，且梯度幾乎不隨低溫黑體發射率的變化而改變。在本文建立的輻射定標模型中，只有將內黑體發射率和低溫黑體發射率提高到0.985以上，才能滿足0.1 K的輻射定標精度要求。

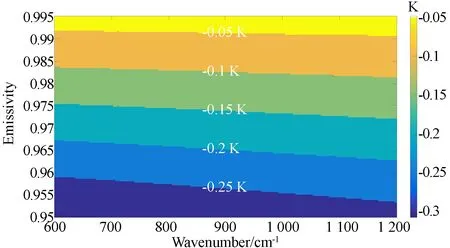
圖5 不同低溫黑體發射率與理想黑體發射率的定標亮溫偏差Fig.5 Brightness temperature differences between calibration with different emissivities of low temperature blackbody and ideal blackbody

此外，根據式(7)可見，不同溫度的場景目標，低溫黑體發射率對輻射定標精度的影響不同。圖6所示是不同低溫黑體發射率下，在參考波數為900 cm-1處，定標亮溫偏差隨場景目標溫度的變化。

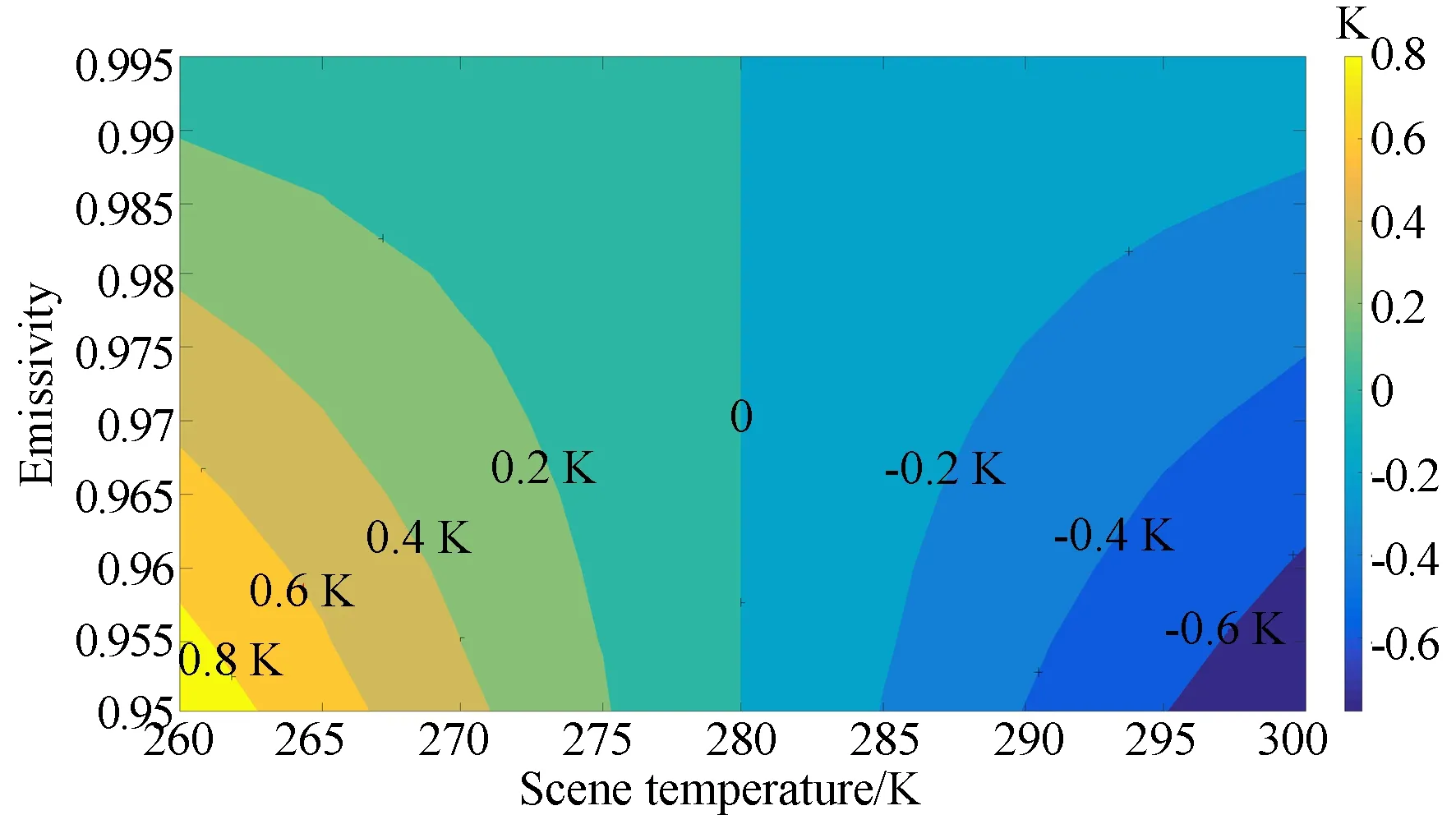
圖6 不同低溫黑體發射率條件下，參考波數900 cm-1處定標亮溫偏差隨場景目標溫度的變化Fig.6 Variations of brightness temperature difference with scene temperatures and emissivities of low temperature blackbody at reference wavenumber of 900 cm-1

由圖6可知，當場景目標溫度與內黑體溫度相同時，定標亮溫偏差為零。在同一低溫黑體發射率情況下，隨著場景目標溫度與內黑體溫度的差異越來越大，定標亮溫偏差也越來越大，輻射定標精度降低。但是隨著低溫黑體發射率的增大，這種變化的梯度越來越小。

3.3 非線性效應

由于探測器的非線性效應不可忽略，因此在輻射定標前必須對非線性效應加以訂正。實際業務中對于CrIS，非線性訂正系數是利用原始光譜低頻帶外信號來估算的；而對于HIRAS，則是在直流電壓給定時通過迭代非線性訂正系數使不同溫度場景目標定標后亮溫與理想亮溫之差最小來動態計算的。本文主要參考CrIS的非線性訂正算法，討論在非線性訂正過程中非線性系數和直流電壓的擾動對輻射定標精度的影響。

3.3.1 非線性系數

在長波波段探測器的非線性效應明顯，在輻射定標前須對測得的目標光譜進行非線性訂正。而不同溫度的場景目標受非線性效應的影響程度不同[21]，因此我們考慮不同場景目標溫度下，非線性訂正后定標亮溫偏差的變化，如圖7所示。

由圖7可知，整體而言經非線性訂正后輻射定標精度能夠提高到10-2K左右的量級。當場景目標溫度與內黑體溫度相同時，定標亮溫差為零。當場景目標溫度高于內黑體溫度時，對于同一場景目標溫度，定標亮溫差隨波數的增大而減小，且這種變化的梯度隨著場景目標溫度的增高而變大。對于某一波數，隨著場景目標溫度的升高，定標亮溫差越來越大，這種變化的梯度也隨著場景目標溫度的升高而變大。當場景目標溫度低于內黑體溫度時，對于同一場景目標溫度，定標亮溫差同樣隨波數的增大而減小。對于同一波數，隨著場景目標溫度的降低，定標亮溫差先增大后減小，在220 K左右出現極值。這是因為我們建立的輻射定標方程中，低溫目標源取的是溫度為105 K的低溫黑體，而不是宇宙背景(深空)。

圖7 不同場景目標溫度下非線性訂正后定標亮溫偏差的變化Fig.7 Variations of calibration brightness temperature difference after nonlinearity correction with scene temperature

根據輻射定標方程，定標輻射DR為：

DR=

RLBB-B(TES).

(8)

根據式(8)，當場景目標溫度等于內黑體溫度或低溫黑體溫度時，即TES=TICT或TES=TLBB時，定標輻射偏差為零。由于定標輻射偏差關于場景目標溫度是連續且可導的函數，故當場景目標溫度介于內黑體溫度與低溫黑體溫度之間時，定標輻射偏差存在極值。而當低溫目標為在軌運行階段的宇宙背景(深空)時，這種極值將不會出現。關于低溫目標變化特征中的極值問題的原因不再贅述。

當干涉儀的非線性效應較大時，即使經過上述的非線性訂正過程，也可能不滿足輻射定標精度的要求。圖8所示是不同場景目標溫度下，在參考波數900 cm-1處，非線性訂正后定標亮溫偏差隨非線性效應系數的變化。

圖8 不同場景目標溫度下在參考波數900 cm-1處非線性訂正后定標亮溫偏差隨非線性效應系數的變化Fig.8 Variations of calibration brightness temperature difference after nonlinearity correction with nonlinearity coefficients and scene temperatures at reference wavenumber of 900 cm-1

圖8表明對于同一場景目標溫度，定標亮溫偏差隨非線性效應系數的增大而增大，且這種變化梯度隨著非線性效應系數的增大而增大。平均來看，當非線性效應系數達到0.04以上時，即使經過非線性效應訂正，定標亮溫偏差也會超過0.1 K，難以滿足輻射定標精度的要求。

在非線性訂正過程中，非線性訂正系數通常不等于非線性效應系數，且在實際情況中非線性效應系數是未知的，須利用已知存在非線性的干涉圖或光譜來估計非線性訂正系數。顯然，通過這種估計方法得到的非線性訂正系數如果存在誤差，則會對輻射定標精度產生影響。圖9顯示了不同場景目標溫度下定標亮溫偏差隨非線性訂正系數偏差的變化。

圖9 不同場景目標溫度下在參考波數900 cm-1處非線性訂正后定標亮溫偏差隨非線性訂正系數偏差的變化Fig.9 Variations of calibration brightness temperature difference after nonlinearity correction with deviations of nonlinearity coefficient and scene temperatures at reference wavenumber of 900 cm-1

由圖9可見，當非線性訂正系數偏差為零時，定標亮溫偏差并不為零，這是因為利用非線性干涉圖或光譜計算得到的非線性訂正系數與儀器本身的非線性效應系數并不完全相等。即使經過沒有偏差的訂正，也不能完全去除非線性效應。另外，在同一場景目標溫度下，隨著非線性訂正系數偏差的增大，輻射定標精度逐漸降低。對于高溫目標，當非線性訂正系數正偏差時，定標亮溫偏差為正偏差；當非線性訂正系數為負偏差時，定標亮溫偏差為負偏差。低溫目標的結論與高溫目標正好相反。相對于低溫目標，高溫目標的定標輻射精度對非線性訂正系數偏差的敏感性更大。從高溫目標的定標亮溫偏差來看，當非線性訂正系數正偏差達到10%以上或負偏差達到20%以上，則輻射定標精度難以優于0.1 K。

3.3.2 直流電壓

由式(5)可知，除非線性訂正系數外，直流電壓V的偏差也會影響非線性效應的訂正效果，進而影響輻射定標精度。在前面分析中，假設直流電壓V是可測得或者計算的。然而，由于探測器和讀出電路設計的限制，目前不少干涉儀并未讀出儀器自發射對應的直流電壓V(記為Vinst)，而是采用參數化的方式獲取[22-23]。以參數化方式獲取的Vinst將帶來更多不確定性，同時隨著儀器狀態的變化，參數化方案的正確性也會隨之降低。

本文采用低頻帶外信號來估算非線性訂正系數，并在設定非線性效應系數和Vinst的仿真數據基礎上，討論場景目標溫度為287 K時，由自發射直流電壓的擾動引起的非線性訂正系數的變化和對非線性訂正效果的影響，其結果如圖10所示。

圖10 非線性訂正結果Fig.10 Result of nolinearity collection

圖10(a)表明，隨著儀器直流電壓的放大(縮小)，非線性訂正系數增大(減小)，但其變化量級不大，大約直流電壓每放大一倍，非線性訂正系數增大1%。圖10(b)表明，當儀器直流電壓增大(減小)時，定標亮溫偏差隨之增大(減小)，且隨著波數的減小，定標亮溫偏差的變化梯度略有增大。直流電壓每放大一倍，定標亮溫偏差將增大0.002 K左右。

4 真空試驗

衛星攜帶的紅外高光譜干涉儀在軌前會進行地面真空測試試驗，通過觀測或物理統計分析獲得一些儀器的定標參數及其對應的不確定度的估計值，這些可以作為儀器定標時定標參數的參考。風云三號E星HIRAS的輻射定標流程如圖11所示，仿真模型只是將實際觀測光譜根據干涉儀的原理用仿真光譜所替代。

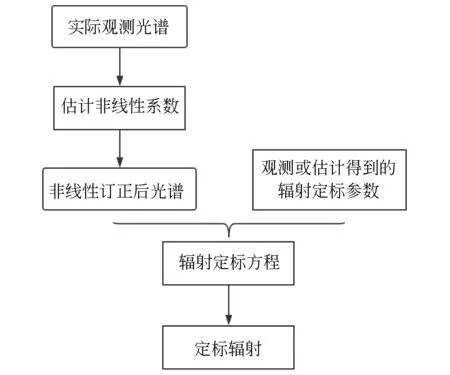
圖11 風云三號E星HIRAS輻射定標流程Fig.11 Flow chart of FY-3E HIRAS radiation calibration

輻射定標參數在仿真模型中是自由給定的，因此可以對每一個輻射定標參數進行敏感性分析，從而得到不同參數對定標輻射影響的特征。然而在實際定標過程中，一方面由于儀器的復雜性，有些定標參數還沒有有效的辦法進行觀測或估計；另一方面，一些未知的噪聲混疊在觀測樣本中，導致定標亮溫與理想亮溫仍有較大的差異。這就給定標精度的提高帶來了困難。

在敏感性分析中，利用仿真模型已經得到了各種不同輻射定標參數變化影響定標輻射的物理規律。因此，在實際定標過程中，可以利用式(9)對輻射定標參數進行迭代，其中RES,k(k=1,2,…,n)表示n次觀測光譜的定標輻射，x1,x2,…,xp表示p個輻射定標參數。當函數J達到最小時，對應的定標參數為最優估計值。地面真空試驗已觀測或估計得到的定標參數可以作為初值，且利用其不確定度給迭代范圍進行一個限定。未知的定標參數可以給定一個初猜值，及相對較大的迭代范圍。

J(x1,x2,…,xp,εES)=

(9)

現取兩組地面真空試驗實際觀測的光譜，觀測的場景目標溫度均為290 K，先利用一組樣本光譜在參考波數900 cm-1處進行迭代，得到輻射定標參數的最優估計值。然后，利用最優估計的輻射定標參數對另一組樣本光譜進行輻射定標，比較輻射定標參數初值和最優估計值所對應的定標精度，其結果如表1所示。

表1 迭代前后的輻射定標參數及輻射定標精度

Tab.1 Radiometric calibration parameters before and after iteration and corresponding radiometric calibration accuracies

定標參數初值3σ不確定度最優估計值εICT0.994(真空試驗得)0.015(真空試驗得)0.979TICT/K290.72(真空試驗得)0.06(真空試驗得)290.69a2/V-10.0169(真空試驗得)10%(真空試驗得)0.016 1εES1(猜值)0.015(猜值)0.996定標精度/K1.261.00

實驗結果可見，迭代后所得的輻射定標的參數估計值得到的定標精度比初值更好，此時得到的這些輻射定標參數的最優估計實際上已經掩蓋了一些未考慮的參數及未知噪聲的影響，因此未必代表的是其對應的物理真值，但有效地提高了輻射定標精度。

由此可見，利用仿真模型分析輻射定標參數的變化對定標輻射的物理規律，結合地面真空實驗觀測或物理統計得到的一些定標參數及其不確定度的估計值，可以通過迭代的方式得到這些輻射定標參數以及一些未測參數的最優估計，從而提高輻射定標精度。

5 結 論

本文利用輻射定標模型，針對內黑體發射率、低溫黑體發射率、內黑體與環境溫度差、非線性系數以及直流電壓的變化對定標輻射的影響進行了敏感性仿真實驗。理論和實驗結果表明，定標輻射偏差的絕對值隨內黑體和低溫黑體發射率的增大而線性減小，與內黑體與環境溫度差、非線性系數(隨場景目標溫度而變化)、直流電壓正相關。

提高內黑體發射率、低溫黑體發射率到0.985以上，控制內黑體與環境溫度差在0.6 K附近可以有效地提高輻射定標精度。有效地控制干涉儀的非線性效應使非線性效應系數小于0.04，且在非線性訂正時，控制非線性訂正系數的偏差低于10%，是實現0.1 K輻射定標精度的先決條件。利用仿真模型總結的輻射定標參數影響定標輻射的物理規律，結合地面真空實驗給出的參數及不確定度的參考，可以利用實測光譜進行參數最優估計，從而提高輻射定標精度。

這種研究方法對于紅外高光譜干涉儀的儀器參數設計有指導性意義，對于輻射定標誤差來源的識別與輻射定標參數的訂正也有重大幫助。本文基于敏感性因子仿真分析的研究方法已經應用在風云三號D星HIRAS的在軌定標誤差識別和E星HIRAS的地面試驗設計和分析中。