裝配式箱涵結構整體可靠度研究

王濤 劉子傲 喬鵬飛 李佳其

摘? 要：裝配式箱涵各預制構件之間的連接至關重要，其接縫處是尤為薄弱的部位，這對結構的可靠性分析提出了較高的要求。文章結合工程實例，首先采用驗算點法進行裝配式箱涵頂板、側墻和底板以及鉸縫處的構件可靠度分析，然后與蒙特卡洛法進行對比，結果表明：兩種方法得到的可靠指標相差很小，均符合規范要求。最后，考慮構件間的相關性進行了箱涵結構體系可靠度分析，計算得到的可靠指標與不考慮構件間相關性時相比結果偏小，也更偏于安全且符合實際。

關鍵詞：驗算點法;裝配式;箱涵;可靠度

Abstract： The connection between precast element of prefabricated box culverts is very important， and its joints are particularly weak， which places higher requirements on the reliability analysis of the structure. Based on engineering examples， the reliability analysis of the roof， side wall， floor and hinge joints of the assembled box culvert is firstly carried out by the checking point method. Then compared with Monte Carlo method， the results show that the reliability index obtained by the two methods differ little and both meet the requirements. Finally， the system reliability analysis of box culvert structure is carried out by considering the correlation among components. The calculated reliability index is smaller than that without considering the correlation between components， which is more secure and practical.

涵洞是公路工程的重要組成部分，傳統的現澆施工方法存在成本高、建設進度緩慢及不易控制施工質量等問題。隨著“標準化設計、工廠化生產、裝配化施工”理念的提出，加之裝配式結構具有可以提升建筑質量、提高效率、縮短工期和方便冬期施工等優勢，使得裝配式箱涵結構受到極大關注。但是，裝配式箱涵結構的整體性能還不能完全等同于現澆，如何保證該類型結構在設計和使用過程中具有足夠的安全性、適用性和耐久性仍是值得研究的問題。

國內外諸多學者在裝配式橋涵結構的破壞和可靠性分析方面進行了大量研究。王二磊等[1]在對高速公路橋涵加固后的可靠度分析中提出對于橋涵結構一般情況下考慮彎曲破壞的失效模式，結構的破壞模式在裝配式箱涵可靠度的研究中至關重要;Awwad等[2]利用有限元軟件SAP2000對108個盒狀涵洞結構進行了分析，研究發現：最大正彎矩一般發生在跨中，最大負彎矩一般發生在頂板和墻的交接面;Gag和Abolmaali[3]通過有限元軟件ABAQUS對涵洞結構模型進行數值模擬分析，并與試驗結果進行了對比，有限元模擬結果與試驗結果比較吻合。李鵬程[4]、羅征[5]、袁桂芳[6]和張曉皖[7]等采用數值模擬和試驗研究等手段對裝配式空心板橋結構鉸縫的受力性能進行了一定的研究。以上對于裝配式橋涵結構的相關研究為裝配式箱涵結構的可靠性研究奠定了基礎，但對裝配式箱涵結構體系可靠度還有待于進一步研究，以便全面把握裝配式箱涵結構的可靠性。

本文依托吉林省白城市“大慶至廣州高速公路雙遼至嫩江聯絡線雙遼至洮南段03A設計段”工程項目，采用驗算點法對其中的四構件裝配式箱涵的構件可靠度和考慮構件相關性的結構體系可靠度進行了研究。

1 工程概況

“03A設計段”裝配式鋼筋混凝土箱涵結構尺寸為3m×2.2m，節段長度為3m。結構頂板、側墻為預制構件，底板為現澆構件，頂板和側墻為肘形鉸接，如圖1所示。采用C40混凝土，HRB400級鋼筋，鉸縫處采用M15水泥砂漿，其構造詳見圖2，箱涵上部填土高度為5m。

2 裝配式箱涵結構可靠度分析

2.1 功能函數的建立

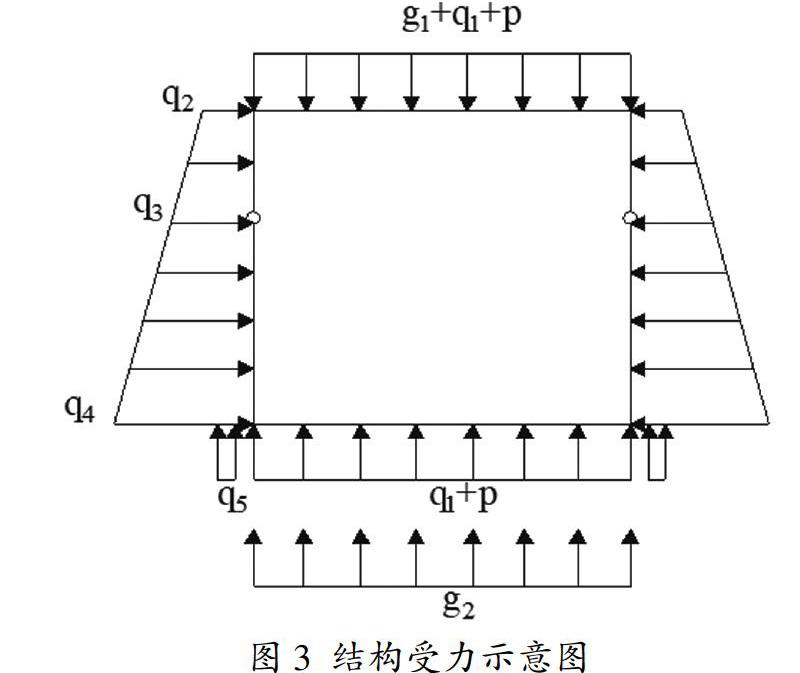
裝配式箱涵結構需要重點關注其受彎構件（箱涵頂板、側墻及底板組成的整體）的抗彎可靠度和受剪構件（鉸縫構造處上下取0.5m作為研究對象）的抗剪可靠度。結構受力形式如圖3所示，其中，g1為頂板自重（kN/m），q1為上部填土體重力（kN/m），p為車輛荷載（kN/m），q2，q3，q4分別為不同位置側向土壓力（kN/m），q5為撐腳土體重力（kN/m），g2為結構整體自重（kN/m）。

式中，f′s為受壓區縱向鋼筋的抗拉強度設計值（kN/m2）;fcd為混凝土軸心抗壓強度設計值（kN/m2）;x為受壓區高度（m），x=（fs·As-f′s·A′s）/（fcd·b），其中fs為受拉區縱向鋼筋的抗拉強度設計值（kN/m2），As為受拉區鋼筋截面面積（m2）;h0為頂板橫截面有效高度（m）;A′s為受壓區鋼筋截面面積（m2）;a′s為受壓區鋼筋合力作用點至受壓區邊緣的距離（m）。

2.2 構件可靠度

對于功能函數中的隨機變量，需要對其概率分布進行統計，表1給出了相關參數特性統計[9-12]。

由驗算點法可知，各個參數對結構可靠度影響程度是不同的，可將影響程度較小的參數當作確定性變量處理。對箱涵頂板、側墻、底板及鉸縫功能函數中各個變量進行敏感性分析，正數為對結構有利的參數，負數為對結構不利的參數，分析結果如表2所示。

由表2可知，對于箱涵頂板敏感程度較大的參數及其排序為：鋼筋抗拉強度設計值>計算跨度>鋼筋直徑>上部填土重力密度>上部填土內摩擦角，其他參數的敏感性較小。因此對箱涵頂板進行可靠度分析時，可將這5個參數作為隨機變量考慮，其他參數均作為確定性值考慮;同理，對于箱涵側墻及底板敏感程度較大的參數及其排序為：鋼筋抗拉強度設計值>計算跨度>上部填土內摩擦角>鋼筋直徑>上部填土重力密度。因此，對箱涵側墻及底板構成的整體進行可靠度分析時，僅將這5個參數作為隨機變量考慮;對于箱涵鉸縫構造處敏感程度的參數及其排序為：鋼筋抗拉強度設計值>上部填土內摩擦角>鋼筋直徑>上部填土重力密度。因此，對箱涵鉸縫構造處進行可靠度分析時，僅將這4個參數作為隨機變量考慮。綜上，采用驗算點法可以得到結構頂板、底板及側墻、鉸縫構造處的可靠指標。蒙特卡洛法是工程界一種運用較廣泛、較實用的計算方法，為了驗證驗算點法的準確性，這里將計算結果與蒙特卡洛法求解結果進行對比，如表3所示。

由表3可知，兩種方法所得可靠指標相差很小，均符合相關規范橋涵結構目標可靠指標限值的規定。因此，采用驗算點法對箱涵結構可靠度進行計算，其結果可靠，還能夠避免蒙特卡洛法大量抽樣以及結果不收斂的弊端。

2.3 體系可靠度

運用前述相關系數的求解方法，可得構件間的相關系數。進一步地可求解是否考慮構件間相關性的結構體系可靠指標，不考慮構件間相關性時以可靠指標最低的構件可靠度作為體系可靠度，計算結果如表4所示。

對比可知，考慮結構構件相關性的串聯體系可靠指標偏小，這一結果與串聯體系可靠度小于其結構中單一構件可靠度的結論相符合。因此，串聯體系在考慮了相對容易失效構件之間的相關性時，其計算結果偏于安全。

3 結論

考慮裝配式箱涵結構的受力特性及破壞模式，建立箱涵結構的功能函數，采用驗算點法對裝配式箱涵結構的構件可靠度和結構體系可靠度進行了分析，得到以下結論：

（1）對比采用驗算點法和蒙特卡洛法計算的裝配式箱涵結構構件可靠度結果，兩者相差較小，均符合規范要求。

（2）考慮構件間相關性得到的結構體系可靠度結果偏于安全，也更加符合實際情況。

參考文獻：

[1]王二磊.高速公路橋涵加固后可靠性研究[D].武漢：武漢理工大學，2004.

[2]Awwad E， Mabsout M， Sadek S， et al. Parametric study of load distribution in four-sided concrete box culverts[J]. Bridge Structures， 2008，4（2）：99-107.

[3]Um D. Finite Element Modeling and Analysis[M]. Solid Modeling and Applications， 2016.

[4]李鵬程.裝配式空心板橋鉸縫破壞原因分析[J].公路與汽運，2018，189（6）：142-145.

[5]羅征，王銀輝，金輝.型鋼-混凝土組合加固裝配式空心板梁橋鉸縫破壞模式及工作性能研究[J].世界橋梁，2018，46（6）：85-90.

[6]袁桂芳.裝配式板梁鉸縫損傷識別模型的研究[J].公路，2017，260（08）：80-86.

[7]張曉皖.裝配式空心板橋橫向鉸接縫設計及改進方法研究[D].長春：吉林大學，2017.

[8]部門交通部公路規劃設計院.公路鋼筋混凝土及預應力混凝土橋涵設計規范[M].人民交通出版社，2002.

[9]王茜.開裂在役鋼筋混凝土梁加卸載剛度與正常使用可靠度分析[D].成都：西南交通大學，2017.

[10]趙基達，徐有鄰，黃小坤，等.混凝土結構設計規范（GB50010-2010）[J].建設科技，2015，346（10）：28-30.

[11]謝開仲，陳家海，王紅偉，等.連續剛構橋施工階段可靠性分析的支持向量機法[J].公路，2018，259（1）：105-109.

[12]趙海龍.可靠性和可靠性靈敏度分析的函數替代方法研究及應用[D].西安：西北工業大學，2015.

[13]李君元.結構可靠性計算方法性能比較研究[D].呼和浩特：內蒙古工業大學，2018.