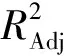煤粉工業鍋爐運行數據與供料參數的相關性研究

劉 振 宇

(1．煤科院節能技術有限公司，北京 100013；2．煤炭資源高效開采與潔凈利用國家重點實驗室，北京 100013；3．國家能源煤炭高效利用與節能減排技術裝備重點實驗室，北京 100013)

0 引 言

在煤粉工業鍋爐中，供料系統通過氣力輸送，將煤粉定量送入燃燒器中供給燃燒。供料的穩定性對鍋爐的穩定運行影響很大。定量計量供料量和供料波動是鍋爐實現自動調節的重要前提。目前煤粉質量流量的直接測量困難[1]，現有的直接測量方法包括電容法、靜電法、摩擦電法、微波法、γ射線法、差壓法等。其中，電容法[2-3]對傳感器固有的檢測場分布要求較高，且由于固相濃度變化引起的電容量變化甚微，對電容分辨率和抗雜散電容的能力要求嚴格，使其對空氣濕度等參數變化敏感，需頻繁標定。靜電法[4-6]由于陣列式靜電傳感器存在局部敏感特性，僅適用于小管徑的密相流測量。摩擦電法[7-8]可測量的煤粉濃度上限很低，目前僅能做到上限45 g/m3。微波法[9-10]的檢測范圍和精度較廣，但受限于設備成本，中小型鍋爐難以采用。γ射線法[11]利用γ射線吸收原理，可達到5%以內的測量精度[12]，但γ放射源的危險性及成本限制了其使用范圍。差壓法利用壓力傳感器，測量供料系統兩點間的壓力差，利用煤粉濃度-差壓的對應關系[13]測量煤粉流量，一般包括文丘里法和彎管法，文丘里法測量精度較高，具有較高的阻力。由于煤粉工業鍋爐一次風沿程經過文丘里混合器，因而具有應用差壓法的基礎。

除了直接測量，鍋爐各種與供料相關的間接參數也可用于衡量供料參數，有學者使用不同方法研究了爐膛壓力與供料量的關系[14-15]。但以往研究重點關注爐膛壓力，對于其他參數，如中間倉稱重、供料鎖氣閥轉速、一次風總壓、煙氣氧含量等與供料參數的關系鮮有報道。本文通過對工業運行數據的分析，對上述參數用于供料參數間接測量時的可靠性及限制進行探討。

1 研究對象及方法

1.1 研究對象

本文數據取自天津華苑58 MW雙燃燒器中儲式煤粉工業鍋爐。煤粉經由制粉站通過氣力輸送儲存于大粉倉中。鍋爐運行時，大粉倉中的煤粉通過中間倉進料閥分別進入中間倉1和中間倉2，隨后通過中間倉出口的供料鎖氣閥進入煤粉混合器中，與來自一次風機(羅茨風機)的空氣混合，形成均勻的氣-固兩相流送入燃燒器。

在鍋爐運行過程中供料鎖氣閥持續運行，通過變頻電機控制轉速，進而調整供料量。中間倉使用自動料位控制，當中間倉稱重降低到900 kg時，中間倉進料閥開啟，將煤粉由大粉倉送入中間倉，直到中間倉稱重升至1 100 kg，中間倉進料閥停止。鍋爐結構及測點布置如圖1所示。各傳感器中，中間倉稱重位于中間倉下側，型號為BK-1680，量程上限1 680 kg；一次風總壓測點位于一次風沿程的混合器入口處，傳感器型號ABB-2600T，量程0～60 kPa，共設置3個，取其中2個數值差較小的測量值，取平均作為有效數據。采用威爾巴流量計測量二次風量和三次風量，壓力上限7 000 Pa，傳感器具有溫度矯正功能，自動矯正為Nm3/h，對應空氣密度1.293 kg/m3；爐膛壓力傳感器量程-1 000～1 000 Pa；煙氣氧含量傳感器量程0～21%，各傳感器數據的更新頻率≥1 Hz。數據獲取時間為2019-11-01—11-30，數據記錄頻率均為1 Hz。

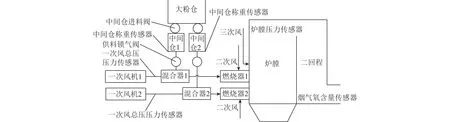
圖1 鍋爐供料系統結構及測點布置Fig.1 Structure of boiler feeding system and arrangement of measuring points

1.2 分析方法

為了分析供料鎖氣閥轉速、粉倉稱重、爐膛壓力、煙氣氧含量用于預測供料性能的可行性及準確性，首先通過變量的物理意義，確定該變量與瞬時供料量、平均供料量、供料波動等供料性能參數的關系。采用決定系數R2，對比不同變量組間擬合優度的差異。R2的計算公式為

(1)

式中，y1為帶入回歸方程得到的參數y的估計值；y2為參數y的實際值；-y為參數y的平均值。

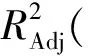
(2)

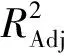
2 數據分析

2.1 中間倉稱重

鍋爐運行時，中間倉進料閥一般以5～10 min為周期交替開啟、關閉。在進料閥關閉的時間段內，中間倉沒有煤粉流入，煤粉唯一的流出途徑為供料鎖氣閥。因此，該時間段內若其他參數不變，可采用中間倉稱重的變化速率計算供料量。

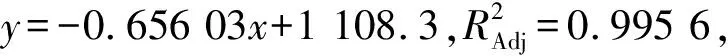
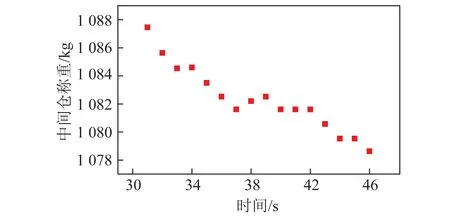
圖2 單卸料周期稱重曲線Fig.2 Single unloading cycle weighing curve

但中間倉稱重用于判斷供料特性也存在以下局限：① 由于稱重傳感器輸出的數據是質量累計值，其分辨率不足以計量瞬時供料量；② 將圖2局部放大可以看出，存在中間倉稱重數據隨時間上升現象，由于該過程中間倉內煤粉只有流出沒有流入，可推斷該信號屬于干擾數據。由于局部干擾數據的存在，使中間倉稱重無法用來計算供料波動。

2.2 鎖氣閥頻率

常見的供料量計量方法是將供料鎖氣閥凹槽中的煤粉填充率和密度視為定值，根據鎖氣閥電機減速比計算出電機頻率-鎖氣閥轉速的關系(供料量=鎖氣閥轉速×每轉容積×煤粉填充密度)。實踐發現，該計算方法準確性和重復性較差，主要是由于不同供料量下煤粉填充密度通常為非定值，因此需要引入其他參數。由于中間倉稱重可準確計量一定時間內的平均供料量，因此可將其作為中間變量，研究鎖氣閥頻率和供料量之間的關系。

在測量數據中篩選出1號供料鎖氣閥運行數據最多的8個電機頻率工況，以及2號供料鎖氣閥運行數據最多的7個電機頻率工況。每個篩選出的電機頻率中，隨機選取5個完整1 100～900 kg中間倉卸料周期，采用2.1節的方法計算每個周期的供料量，并計算5個周期供料量的均值和標準差，結果如圖3所示。

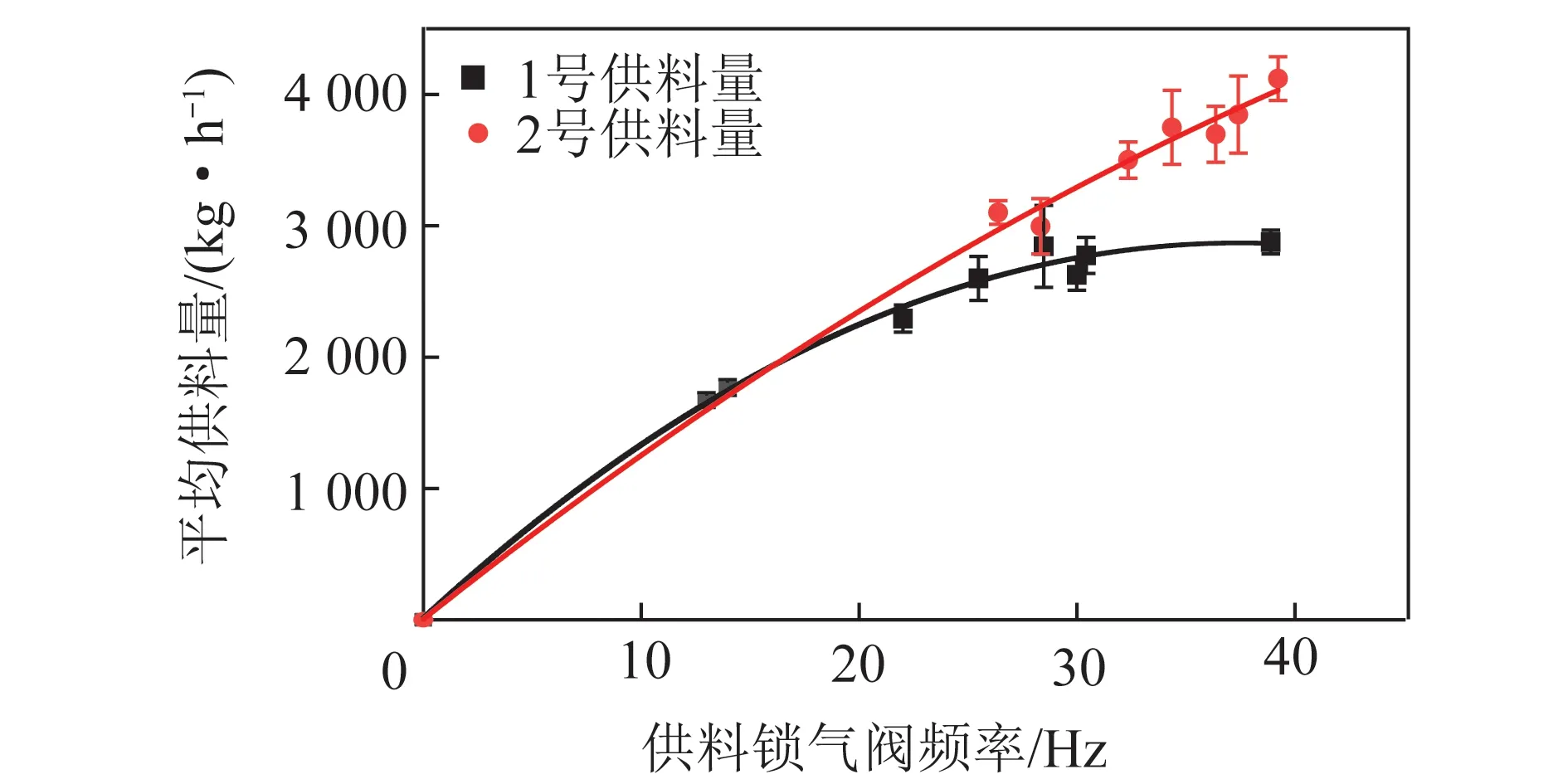
圖3 鎖氣閥頻率-供料量的關系Fig.3 Relationship between frequency of air lock valve and feed quantity

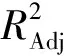
不同鎖氣閥的的衰減規律存在差異，該鍋爐2個鎖氣閥的供料曲線在低頻下較接近理想值，且差距很小，但在20 Hz以上開始出現差異，其原因有待進一步探究。

2.3 一次風總壓

一次風從羅茨風機出口依次經過混合器、一次風管、回流帽進入燃燒器。從物理意義角度，風機出口氣流的總能量損耗，等于沿程煤粉-空氣-管壁之間的摩擦、煤粉加速、文丘里加速-擴散等作用造成的能量損失之和，該損耗可用一次風壓總壓進行表征。

當供料量為0時，一次風沿程阻力計算公式為

(3)

其中，ΔPa為無煤粉時的一次風總阻力，Pa；λ為直管段的摩擦因數；ζ1為彎管的局部阻力系數；ζ2為文丘里混合器的局部阻力系數；l為一次風管長度，m；d為一次風管直徑，m；ρ為空氣密度，kg/m3；u為一次風速，m/s。λ、l、d、ζ1、ζ2屬于結構參數，在不改變文丘里噴口口徑的情況下為定值。在輸送煤粉時，沿程阻力上升，導致風機出口空氣密度ρ上升，u降低，兩者反向變化，且由于羅茨風機屬于恒容積式風機，風量下降速率較平緩，因此在壓力變化不大的情況下，ρu2可近似按照定值處理。因此ΔPa可取煤粉輸送量為0的工況下一次風總壓的平均值，結果為：1號供料器ΔPa1=20.54 kPa，標準差0.69 kPa；2號供料器ΔPa2=21.64 kPa，標準差0.74 kPa。

供料量>0時，一次風沿程阻力增加，此時一次風總壓和空載一次風總壓關系[16]為

(4)

式中，ΔP為氣固混合物通過文丘里時的總阻力，Pa；k為未知系數；μ為固氣比，kg/kg；ms為煤粉質量流量，kg/s；ma為一次風空氣質量流量，kg/s。

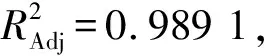
根據式(4)，確定k值后，可通過供料量>0時一次風總壓ΔP計算煤粉流量，即

(5)

根據式(5)計算2.2節中1號供料器8個工況和2號供料器7個工況下的一次風總壓均值(k1和k2)，結果如圖4所示。

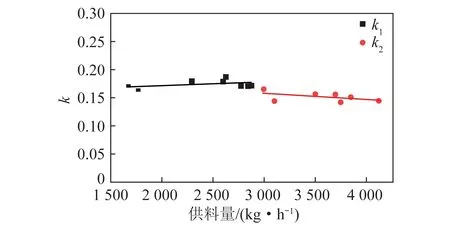
圖4 系數k計算值Fig.4 Calculated value of coefficient k

由圖4可知，k1均值為0.174 1，標準差為0.007 2，k2均值為0.151 3，標準差為0.008 5，離散系數約為5%，精度可滿足工業計算要求。

式(5)中質量流量ma的計算方法為：空氣溫度(41±4) ℃，空氣密度1.124 kg/m3，一次風管內徑135 mm，平均氣速25 m/s，空氣質量流量0.402 kg/s(或1 447 kg/h)，代入式(5)得到

ms1=0.404 6ΔP1-8 310

(6)

ms2=0.441 8ΔP2-9 564

(7)

式中，ms1、ms2分別為供料鎖氣閥1、2的供料量，kg/s；ΔP1、ΔP2分別為供料系統1、2的一次風總阻力，Pa。

根據式(6)和式(7)，可得到鍋爐總供料量mss為

mss=0.404 6ΔP1+0.441 8ΔP2-17 874

(8)

2.4 爐膛壓力

根據理想氣體狀態方程

PV=nRT

(9)

其中，P為壓力，Pa；V為體積，m3；n為氣體摩爾數；R為常數；T為溫度，K。其他參數不變、供料量增加時，若燃料燃盡率無明顯下降，則煤粉放熱量增加，爐膛溫度T升高，由于爐膛體積V和助燃風量n均不變，因此爐膛壓力P升高。要得到供料量-爐膛壓力絕對值的關系，需要確定與熱態相同二次風量、三次風量、引風機頻率等相同工況下的冷態爐膛壓力空白值。由于鍋爐長期處于運行狀態，缺少可供參照的冷態數據，因此難以分析供料量-爐膛壓力的關系，僅可通過熱態爐膛壓力和一次風總壓的波動，推斷爐膛壓力波動-供料波動的關系。

選取93組取樣時間為300 s、頻率1 Hz的數據，每組數據取樣時鍋爐各設備參數保持不變，根據式(8)計算瞬時供料量，結果如圖5所示。

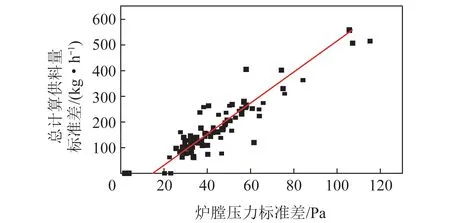
圖5 供料量標準差-爐膛壓力標準差Fig.5 standard deviation of feed quantity-standarddeviation of furnace pressure

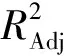
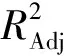
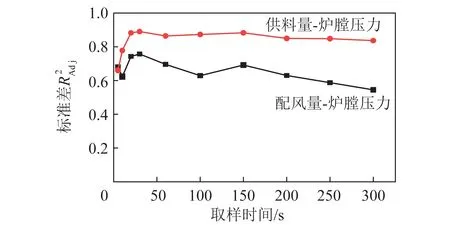
圖6 配風量/供料量波動-爐膛壓力波動Fig.6 Distribution air volume/feed volume fluctuation-furnace pressure fluctuation

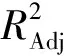
2.5 煙氣氧含量

氧含量和供料量、二次風量、三次風量、煤粉燃盡率等參數關聯較大，與爐膛壓力不同，鍋爐氧含量有固定的空白值，即空氣中的氧含量0.21。因此可使用煙氣氧含量推斷供料量和供料波動，耗氧量的計算公式為

Q(O2)=(A1+A2+A3)[0.21-w(O2)]

(10)

式中，Q(O2)為鍋爐耗氧量，Nm3/h；A1、A2、A3為總一次風量、總二次風量、總三次風量，Nm3/h；w(O2)為氧含量。

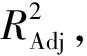
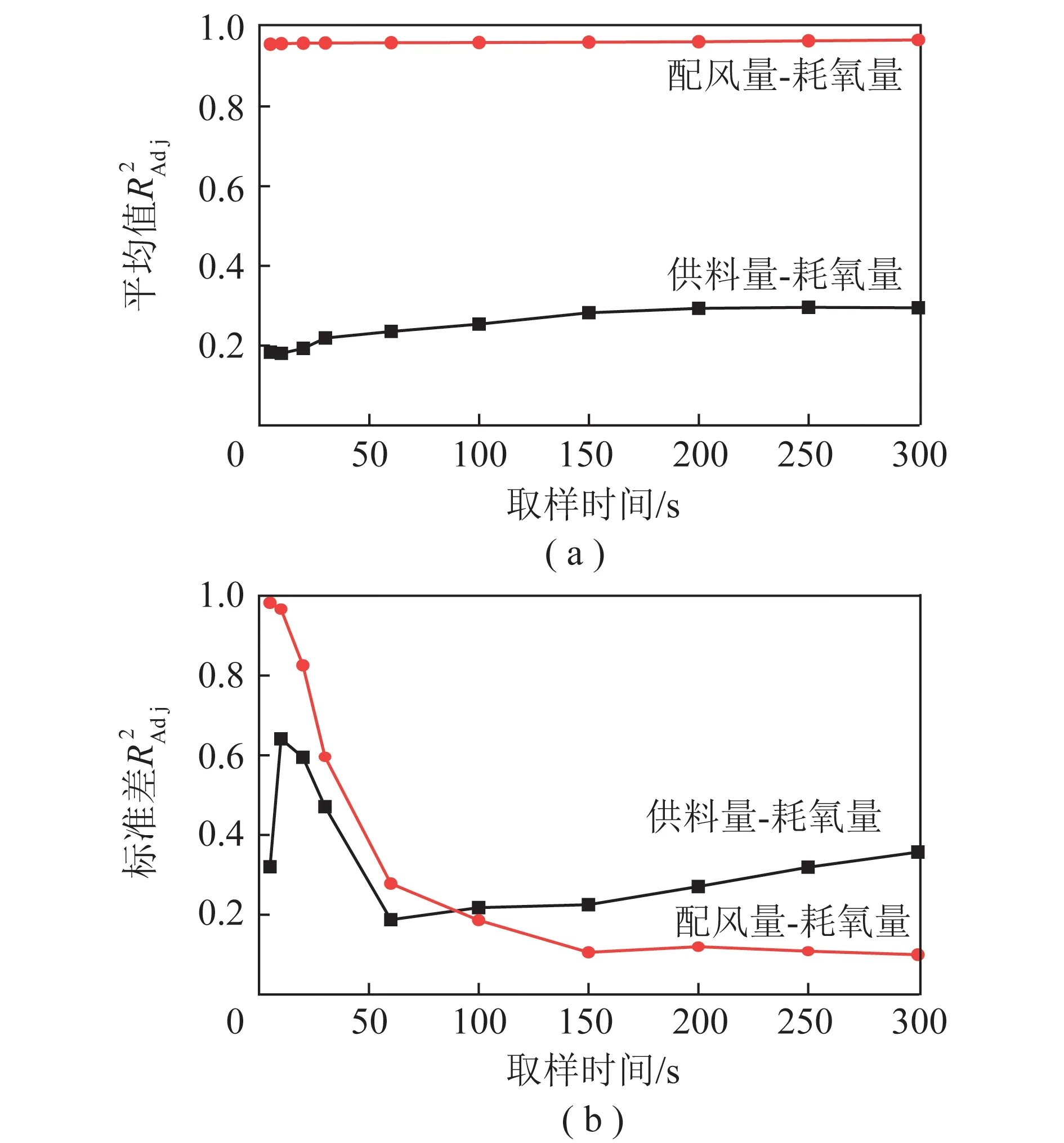
圖7 耗氧-供料/配風Fig.7 oxygen consumption-feed/air distribution

在較長時間跨度上，該鍋爐同樣供料量下的耗氧量有較大變化，主要是由于該鍋爐煤粉為2種熱值相差較大的煤粉摻混而成，說明2種煤粉的摻混比例控制可能較差，導致成品煤粉的熱值/元素組成存在較大波動。

3 結 論

1)中間倉進料閥關閉時，可通過中間倉稱重數據進行線性回歸，以高準確度計算供料器300 s周期內的平均供料量。但受限于稱重傳感器的分辨率及局部干擾數據，中間倉稱重無法用于瞬時供料量或供料波動。

2)采用供料鎖氣閥轉速計算供料量，需假設鎖氣閥凹槽填充率和填充密度為定值，鎖氣閥低轉速下供料曲線符合該假設。但隨著鎖氣閥轉速增加，有效進料/出料時間的縮短和出口壓力的提高，使供料量隨轉速的增長率以二次曲線邊際遞減，且不同鎖氣閥的供料量遞減規律存在個體差異。