高速公路交通事故后基于優化的強制換道研究

王正武，鄒文竹，郝威

(長沙理工大學 交通運輸工程學院,湖南 長沙 410114)

高速公路發生交通事故后，事故點上游車輛需換道來避開事故車道。目前，已有不少學者研究了換道問題。換道問題分為換道決策研究、換道模型研究及換道軌跡研究等。換道決策的內容包括：意圖產生、目標車道選擇及換道條件評估等。在換道決策研究方面， Kanaris[1]等人針對自動高速公路系統中車輛換道問題，提出了基于最小安全距離換道條件的評估方法。Talebpour[2]等人提出了車聯網環境下，基于博弈論的換道決策模型。Meng[3]等人引入結構平衡理論，考慮車輛間的相互影響，建立了滾動時域控制的換道博弈模型。Nilsson[4]等人按是否換道、何時換道及如何換道3步，分析了自動駕駛車輛的換道決策問題。Hidas[5]為智能交通系統提出了強制換道和協同換道模型，并通過仿真實驗，驗證了擁擠情況下強制換道和協同換道的可行性。李玉潔[6]等人分析了施工區不同換道點道路交通狀態的變化特性和最佳換道點的選擇問題。李珣[7]等人利用威脅度函數，刻畫了多車輛間的相互關系，建立了車、路協同環境下考慮局部區域車輛狀態的協同換道規則模型。李娟[8-9]等人分別建立了自由換道、強制換道及協作換道3種換道方式的換道模型和跟隨車與換道車之間的最小安全距離模型。吳江玲[10-11]等人建立高速公路強制換道持續時間的生存模型，分析了車輛類型和換道時間對換道耗時的影響。在換道軌跡研究方面，現有研究以幾何曲線法為主。Nelson[12]為構建曲率連續的自動車輛導引軌跡，首創了多項式軌跡曲線方法。Piazzi[13]等人提出五次多項式軌跡規劃方法，保證了自動駕駛車輛軌跡的平坦性和可執行性。游峰[14]等人考慮車輛間的相互影響，基于換道安全，提出了面向無人駕駛車輛的協同換道軌跡規劃方法。已有的研究中，多數均假設車輛勻速換道，很少考慮減速換道的情況，且都是研究的單車輛換道行為。實際上，若目標車道車頭間距合適，后車也可能跟隨前車一起換道。大多數車輛換道是基于規則選擇可行換道點進行換道，很少基于優化的方法來確定換道點。而且，在基于規則選擇換道點時，很少考慮前車換道點的選擇對上游車輛運行狀況和換道點的影響。因此，作者擬基于車流波理論，確定高速公路交通事故影響區及目標車道上不同位置車輛的運行速度，以換道距離和最小安全距離等為約束條件，構建跟車換道可行點模型；以換道車輛縱向行駛距離之和最小為目標，建立車聯網環境下換道可行點及方式的協調優化選擇模型，以提高交通事故影響區的運行效率。

1 基于優化的換道模型

1.1 問題描述

高速公路上交通事故發生后，事故點可通行的車道數減少，事故點上游的部分車輛需強制換道。本研究以雙向四車道高速公路因交通事故導致一個車道封閉的情況(如圖 1所示)為例。設事故發生時刻為t0，恢復通車時刻為tf，t0至tf時間內事故路段上單向交通量為 Q(忽略事故路段交通量的波動)；在t0時刻，事故點上游車輛運行速度均為v0，事故車道上車輛i的位置為[Xi(t0),Yi(t0)]，目標車道上車輛 k的位置為[Xk(t0),Yk(t0)]，事故影響區長度為S。

圖1 事故路段車輛換道場景Fig. 1 Lane-changing scene on accident link

在車聯網環境下，高速公路交通事故影響區車輛換道的問題可描述為：根據初始時刻事故路段所有車輛的位置和速度信息，確定t0至tf時間內任意時刻事故影響區各位置車輛的運行速度，計算事故車道上各位置車輛的跟車換道可行點，并以換道車輛縱向行駛距離之和最小為目標進行優化，確定事故車道上各車輛的換道點、換道方式(單車換道或跟車換道，圖1中事故車道上車輛1和2就是跟車換道、車輛i+2、i+3就是單車換道)。

1.2 影響區模型

交通事故發生后，事故點上游車輛基于車聯網獲取實時信息，目標車道上的車輛將采取制動措施，從而形成車流波并向上游傳播，初始時刻t0至結束時刻tf時間段Δf內傳播的距離就是事故影響區長度S。

式中：vw是波速；CII為事故點要求的二級服務水平下的最大服務交通量(也可以取為盡快疏散交通需保持的最大交通量或其他值)；KII為CII所對應的密度；K為事故開始時事故車道上車流密度，K= 0.5Q/ v0。

設目標車道的車輛均以減速度a勻減速到最佳車速vII后保持勻速行駛，直到通過事故點，t0至tf時間內任意時刻t影響區內車輛k的運行速度為：

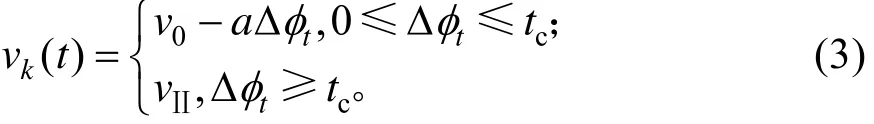
式中：tφΔ為車輛從t0時刻到t時刻行駛的時間；tc為減速時間；vII為最佳車速。

陳凱賢[15-16]等人分別針對高速公路事故影響區域和高速公路施工區的車輛速度限制進行了研究。在本研究中，為了保證車輛的最大通行效率，最佳車速vII為二級服務水平下密度KII時對應的速度。減速時間的計算式為：

1.3 跟車換道可行點模型

事故發生后，設事故車道上的車輛在換道前仍以初始速度v0勻速前行，在前行過程中，不斷尋找換道可行點，在選擇的換道可行點以縱向減速度ax進行減速換道，達到目標車道的運行車速vII后跟隨目標車道上的前車勻速行駛。換道可行點包括單車換道可行點和跟車換道可行點2類。在單車換道可行點的基礎上，基于最小安全距離約束判斷是否能后續m輛車跟車換道。

設車輛i選擇換道點y在t時刻完成換道后目標車道上的前、后車分別為k和k+1，車輛i的單車換道可行點集合為Ri，則Ri可表示為：

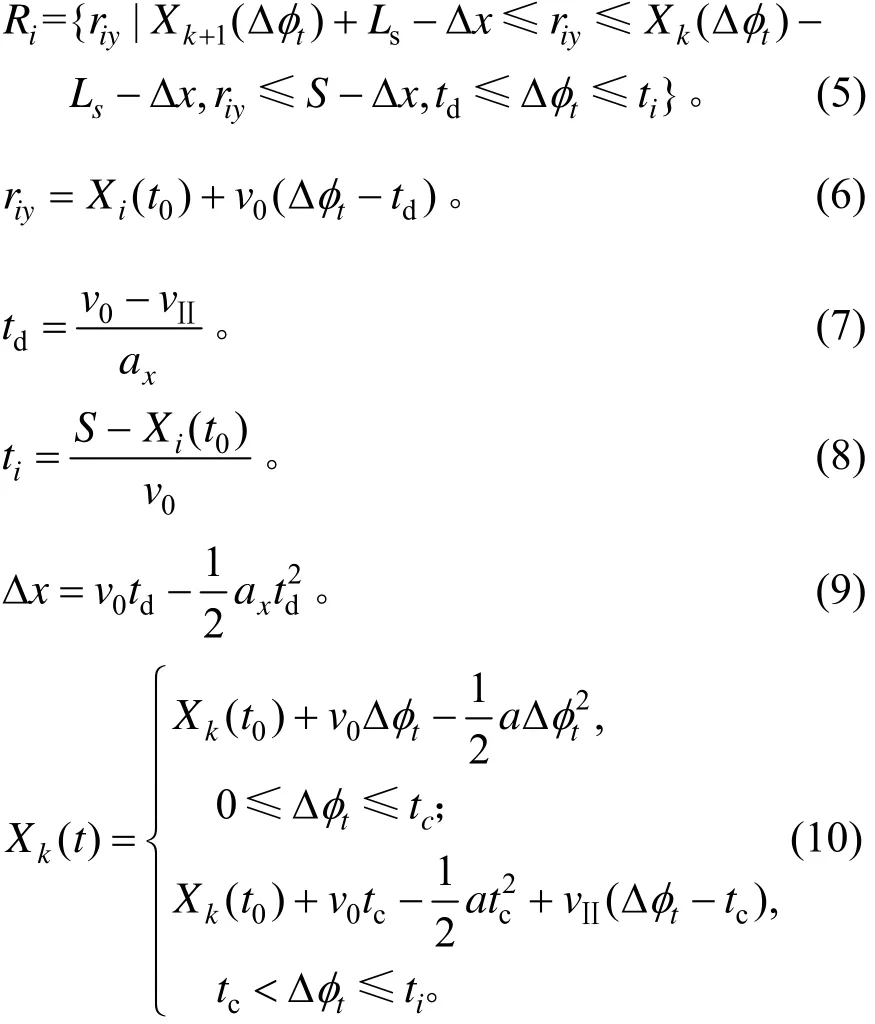
式中：riy為車輛i的換道點y的橫坐標；td為車輛換道所需的時間；ti為換道車輛i在事故車道上以初始速度 v0勻速行駛到達事故點的最長時間；Δx為車輛i換道過程中行駛的縱向距離；Ls為車輛速度vⅡ時目標車道上車輛間的最小安全距離。

式(5)表示單車換道可行集應滿足的約束分別為：車輛i從換道點y開始換道，完成換道后與目標車道上前、后車k和k+1的距離應滿足最小安全距離；車輛i的換道點y應在最晚換道點之前；車輛i換道應該在td到ti時間段內完成。

式(6)表示車輛i在t時刻能夠完成換道時的可行換道點位置；式(7)表示換道所需的時間即換道車輛完成橫向移動所需的時間；式(8)保證車輛在時間段ti內完成換道，即在到達事故點之前完成換道；式(9)表示車輛 i換道所行駛的縱向距離；式(10)表示目標車道上車輛k在任意t時刻的縱向位置。

在車輛i和車輛i-1單車換道可行點集合分別為Ri和Ri-1的基礎上，判斷哪些可行點可進行跟車換道的可行點。若車輛i跟隨前車i-1換道，則車輛i的跟車換道可行點的集合為：

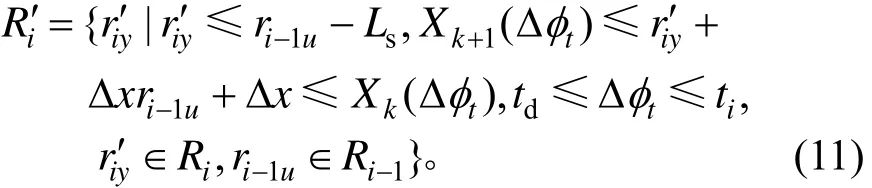
式中：iyr′為車輛i的換道點y的橫坐標；1iur-′為車輛i-1選擇換道點u的橫坐標位置開始換道。

式(11)表示車輛 i跟車換道可行集應滿足的約束分別為：車輛i與前車i-1之間換道點的距離應滿足最小安全距離；完成換道后，車輛i與前車i-1進入目標車道，且處于相同的車輛k和k+1之間。車輛i換道應該在td到ti時間段內完成。

1.4 跟車可行點的優化選擇模型

高速公路上發生交通事故之后，若事故點上游車輛換道不及時，將可能導致二次事故的發生，進而加劇交通擁堵。為避免發生二次事故，處于事故點上游的車輛應盡快換道至目標車道以遠離事故點。因此，本研究目標是使影響區內所有換道車輛在事故發生時刻至完成換道時刻所行駛的縱向距離之和最短，建立的目標函數為：

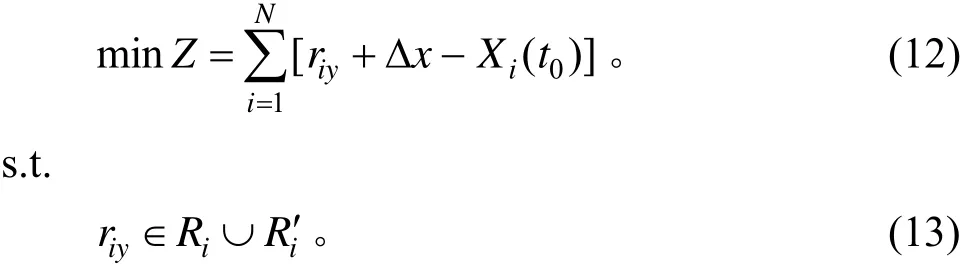
式(12)表示影響區上所有需要強制換道N輛車完成換道時所行駛的縱向距離之和最短；式(13)表示換道可行點應屬于單車換道可行點或跟車換道可行點。

通過這些優化模型，可同時確定所有換道車輛最優的換道點組合和換道方式組合。

2 求解流程

根據強制換道模型的特點，在單向雙車道高速公路發生交通事故的情況下，以事故車道上事故區上游影響區內的車所有輛為研究對象，其求解步驟為：

1) 輸入初始速度、車流量、直線行駛減速度及換道縱向減速度等參數，計算事故影響區域長度、最佳車速、需要強制換道的車輛數、減速至最佳車速的時間及換道的時間等參數。

2) 計算需要強制換道的每一輛車在任意時刻完成換道時的縱向位置。若滿足與前、后車的最小安全距離，則將該時刻對應的換道點位置放入集合Ri中。

3) 若車輛完成換道，則更新車輛位置。在單車換道的基礎上，根據式(11)判斷車輛是否能進行跟車換道，得出車輛的跟車換道點的集合iR′。

4) 利用整數規劃的方法，求出目標函數的最優解。

5) 輸出每一輛車的換道點位置及換道方式。

6) 更改初始參數設置，重復步驟1)～5)。

3 算例分析

有一條雙向4車道高速公路，因交通事故導致一個車道封閉的情況，如圖1所示。設計了2個實驗來驗證該方法的有效性，分析初始交通量和車速對換道方式、換道點的影響。①實驗 1，僅變化初始交通量Q，分析初始交通量對換道方式、換道車輛平均縱向距離的影響。②實驗 2，僅變化初始速度v0，分析初始速度對換道方式、換道車輛平均縱向距離的影響。

3.1 參數說明

針對實驗 1,2，共設計了 5組實驗參數。利用式(1),(3),(5)和(8)及交通流3個基本參數之間的關系等，得到影響區長度S和需強制換道的車輛數N等的計算值。初始流量可反映車輛間距，初始速度可反映車輛間最小安全距離。因此，通過初始流量和初始速度2個參數來反映在不同條件下對車輛換道點、換道方式的影響。

在實驗1中，第一組設置已知參數為：初始流量1 600輛/h，二級服務水平下的最大服務交通量1 400輛/h，初始速度25.0 m/s，直線行駛減速度2 m/s2，換道縱向減速度1.5 m/s2，第二、三組的初始速度固定不變，初始流量分別為1 700和1 800輛/h。在實驗2中，第四、五組的初始流量固定不變，初始速度分別為22.2和27.8 m/s。

通過計算可得，最佳車速為18.5 m/s固定不變。在實驗1中，由于只有初始車流量的變化，隨著車流量的增加，事故影響區的長度會增加，分別為8 300,13 000和18 200 m；需要強制換道的車輛也會增加，分別為73,123和182輛；直線行駛減速時間為3.2 s，換道時間4.3 s。在實驗2中，由于只有初始速度的變化，隨著初始速度的增加，事故影響區的長度會縮短，分別為9 100,8 300和7 700 m；需要強制換道的車輛也會減少，分別為91,73和62輛；直線行駛減速時間則會增加，分別為1.9,3.2和4.6 s；換道時間也會增加，分別為2.5,4.3和6.2 s。

3.2 結果分析

利用 Matlab語言編程，求解所構建的優化模型，輸出車輛的換道起始點和換道方式。實驗1結果表明：隨著初始流量的增加，車輛跟車換道的概率分別為 36.9%,28.4%和 36.8%。流量適中時，車輛跟車換道的概率更低。實驗2結果表明：隨著初始速度的增加，車輛跟車換道概率也隨之增加，分別為7%,36.9%和38.7%。因此，在流量較低或較高、以及車速較高時，車輛更應選擇跟車換道來提高換道的效率，從而盡快遠離事故影響區。

2個實驗 5組數據對應的計算結果分別見表1,2。從表1,2中可以看出：①利用該模型，能優化并確定換道車輛的換道點、換道方式，表明了該方法的有效性。②初始流量和初始速度的變化導致換道車輛的換道點發生了顯著變化，導致跟車換道的車輛數、跟車換道的車輛組合也發生了較大的變化，初始流量和初始速度對換道點、換道方式均有顯著影響。③實驗1中，初始流量從1 600輛/h增加到1 700輛/h再增加到1 800輛/h時，影響區內所有換道車輛在事故發生時刻至完成換道時刻所行駛的縱向距離之和Z增加了144.2%，Z對初始流量的彈性從11.19變化到7.43。表明：換道車輛縱向行駛距離之和與初始流量正相關，而且隨著初始流量的增加，換道車輛縱向行駛距離之和的變化率將越來越小。換道車輛的平均縱向行駛距離從增加 1.0%到減少 2.9%，相對于初始流量的彈性從0.16變化到-0.49。表明：增加初始流量，換道車輛的平均縱向行駛距離是增是減不定，但換道車輛縱向行駛距離之和的變化率將越來越大。跟車換道車輛比例從減少23.9%到增加35.6%，跟車換道車輛比例對初始流量的彈性從-3.83變化到6.05。表明：增加初始流量，跟車換道車輛比例是增是減不定，但換道車輛縱向行駛距離之和的變化率將越來越大。④實驗2中，初始速度從22.2m/s增加到25m/s再增加到27.8m/s時，影響區內所有換道車輛在事故發生時刻至完成換道時刻所行駛的縱向距離之和Z從減少18.1%到增加3.3%，Z對初始速度的彈性從-1.43變化到 0.30。表明：增加初始速度，換道車輛縱向行駛距離之和是增是減不定，但換道車輛縱向行駛距離之和的變化率將越來越小。換道車輛的平均縱向行駛距離增加了 24.2%，z對初始速度的彈性從0.16變化到1.95。表明：換道車輛的平均縱向行駛距離與初始速度正相關，而且隨著初始速度的增加，換道車輛的平均縱向行駛距離的變化率將越來越大。跟車換道車輛比例從增加481.9%到增加1.0%，跟車換道車輛比例對初始速度的彈性從38.2變化到0.09。表明：增加初始速度，跟車換道車輛比例也會增加，但換道車輛縱向行駛距離之和的變化率越來越小。

表1 實驗1的計算結果Table 1 Calculation result of Experiment 1

表2 實驗2的計算結果Table 2 Calculation result of Experiment 2

4 結語

基于最小安全間距和換道距離等，構建了車聯網環境下高速公路發生交通事故后優化車道的強制換道模型，獲取了優化的換道點和換道方式，得到的結論為：

1) 利用模型優化確定了換道車輛的換道點和換道方式，并表明該方法的有效性。

2) 初始流量和初始速度對換道車輛的換道方式、換道點均存在顯著影響。換道車輛縱向行駛距離之和與初始流量正相關，換道車輛的平均縱向行駛距離、跟車換道車輛比例均與初始速度正相關。增加初始流量，不能確定換道車輛的平均縱向行駛距離和跟車換道車輛比例的增減。同樣，增加初始速度，也能不確定換道車輛縱向行駛距離之和的增加。

后續的研究將分析多因素共同作用對換道方式和換道點的影響。