求條件概率的兩種方法辨析
2020-05-14 13:44:25丁遠洪
基礎教育論壇·上旬 2020年4期
丁遠洪
摘要:條件概率是概率論基礎知識中的一個基本概念,是積事件概率和全概率公式的基礎,但是這一概念往往不被學生重視。學生對求條件概率的公式法和縮減樣本空間法容易混淆,對這兩種方法沒有深刻理解,掌握本質。文章主要對求條件概率的兩種方法進行對比,找出兩種方法的異同點。
關鍵詞:條件概率;公式法;縮減樣本空間法
從近些年的高考數(shù)學試題來看,對概率統(tǒng)計題的解題能力的要求逐年提升,這就要求教師在講解解題的方法和過程中要講深、講透,分辨出正確與錯誤的解題方法,并找出錯誤原因,弄清問題本質。
例如,在講解“條件概率”這一知識點時,筆者發(fā)現(xiàn)很多學生對求條件概率的兩種方法容易混淆,不能理解問題的本質,導致容易出錯。以下是筆者在教學實踐中的一些思考和小結。
一、知識呈現(xiàn)
條件概率計算的兩個一般方法。
方法1:公式法。

解析:用求條件概率的兩種方法求解。設“第一次拿出綠色小球”為事件A,“第二次拿出綠色小球”為事件B。

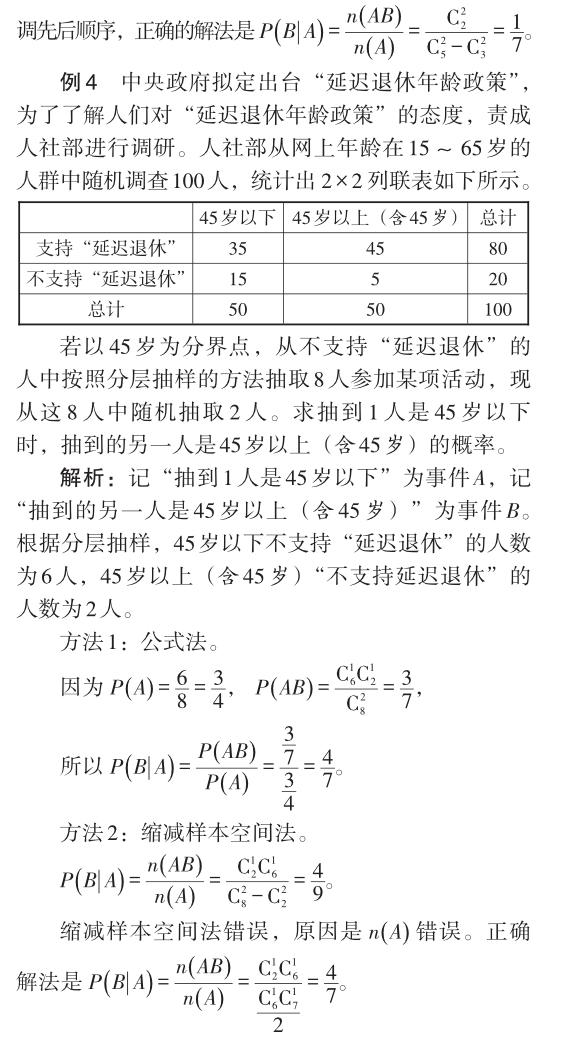
通過用公式法和縮減樣本空間法求解以上四道例題的對比與分析,我們發(fā)現(xiàn)兩種方法各有優(yōu)勢和劣勢。但是,在求沒有事件發(fā)生先后順序下的條件概率時用縮減樣本空間法計算容易出錯,即縮減樣本空間法有一定的局限性;用公式法不容易出錯,故公式法是通性、通法。在求條件概率時要深刻理解兩種方法的異同點和本質,認真審題,采用正確的方法求解,得出正確的結論。
參考文獻:
[1]嚴小寶.淺談條件概率[J].職業(yè)教育研究,2011(4).

