一種適用于泛克里金趨勢函數的優化方法?

楊金璇 潘 懋 劉鈺洋 雷征東 吳耕宇

（1.北京大學地球與空間科學學院造山帶與地殼演化教育部重點實驗室 北京 100871）

（2.北京大學石油與天然氣研究中心 北京 100871）（3.中國石油勘探開發研究院 北京 100083）

1 引言

近幾年，三維地質屬性建模中的確定性建模被廣泛應用在油氣勘探、開發等領域。確定性建模由儲層地震學方法、儲層沉積學方法和地質統計學克里金插值方法組成［1］。地質統計學方法根據待估點周圍的若干已知信息，應用變異函數對待估點未知值做出無偏最優估計。目前廣泛應用于空間域或時間域自然變量的定量化描述等眾多領域［1］。簡單克里金和普通克里金應用最廣泛［2］，但先驗條件嚴苛，大部分地質數據都難以滿足，因此這兩種方法的插值效果難以保證。

泛克里金插值是處理隨機變量非平穩插值問題的方法，結合地質變量在一定范圍內的變化規律進行建模，并且沒有嚴苛先驗條件，適用于絕大部分非均質性比較強的儲層。楊功流［5］等對泛克里金插值方法和普通克里金插值方法進行對比研究，一方面在非平穩的地磁場數據的插值處理中應用兩種方法，另一方面對比兩種方法的插值效果。實例驗證結果顯示，使用泛克里金插值得到的地磁圖更加符合地磁場的特征，證明對非平穩地質數據插值問題，泛克里金方法更適用。

然而，在廣泛的實際應用中，泛克里金方法的理論優勢并不明顯。相較于其他簡單快速算法，其精度優勢比較微弱。目前，對于泛克里金插值精度的研究已成為熱點。李龍［6］結合回歸分析，應用泛克里金插值方法對大氣參數進行插值，獲得更高精度的AOD融合效果。王長虹等［8］在巖土參數隨機場分析中，將泛克里金插值方法與多重分型理論相結合，度量局部空間的奇異性。趙愛梅等［11］研究泛克里金插值效果對變異函數的敏感性。何濤等［12］基于泛克里金插值的時間復雜度，研究趨勢函數參數的估計。

本文考慮，對于泛克里金方法的使用前提是樣品點數據滿足正態分布，但是對于泛克里金方法來說，其插值結果依賴于反應地質變化規律的趨勢函數，而滿足正態分布不能保證研究區數據具有一定變化規律，即無法保證趨勢函數的精度。本文對于趨勢函數的模擬建立在殘差分析的基礎上，對樣本數據進行重采樣，提高插值樣品數據的相關性及結構性，切合泛克里金方法的本質。

趨勢函數是泛克里金插值方法中用于表達地質變量變化趨勢的函數［4］，趨勢函數的精度直接影響插值結果的空間性和隨機性，甚至插值結果的有效性，因此趨勢函數的擬合是泛克里金插值過程中最重要的問題之一。傳統的趨勢函數擬合建立在簡單的多元線性函數擬合的基礎上，本文提出，在傳統擬合趨勢函數的基礎上，應用殘差分析，將在95%置信度下判別為異常點的實驗點剔除，將提升趨勢函數的擬合精度。

2 數學原理介紹

2.1 泛克里金方法概述

泛克里金方法是一種線性無偏最優的空間插值計算方法，研究的非平穩區域化變量，包括趨勢與殘差兩個部分，其數學表達如下：

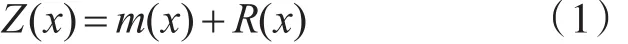
式中，m(x)是趨勢函數，R(x)是殘差。趨勢函數表示區域化變量在研究區內的某種明確的變化規律，是隨機變量Z(x)的期望，有：

殘差是表示趨勢函數波動情況的局部量，是隨機變量在趨勢附近擺動的隨機誤差。在理論上，其期望值為零，且滿足二階平穩條件。

在泛克里金方法中，對于估計值的估計，就轉化為對m(x)與R(x)的估計。對于趨勢函數，可以用多元線性函數對其進行擬合。對殘差的R(x)的估計，使用泛克里金方程組進行求解，即：

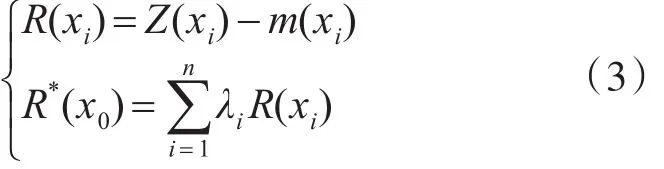
式中，R*(x0)是待插點的最優估計值，R(xi)表示已知樣品的殘差計算值，λi表示R(xi)的泛克里金權重系數。

泛克里金的目標函數為

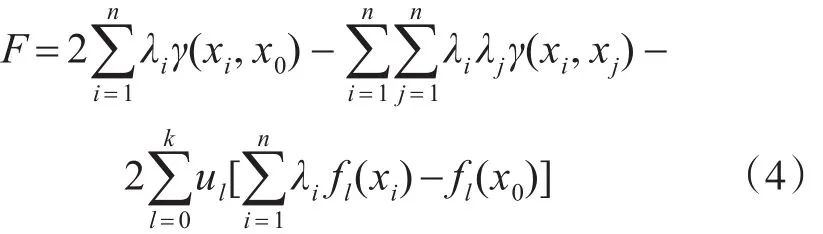
式中，γ是變異函數。

變異函數γ是度量隨機變量空間相關性的工具，在泛克里金插值方法中有重要意義［3］。實驗變異函數是兩個樣品點的函數，公式如下：

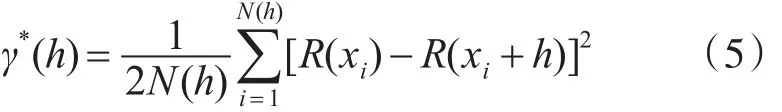
式中，h是滯后距，γ*(h)為實驗變異函數，N(h)為滯后距為h時的點對數，R(xi)與R(xi+h)是實驗點xi和 xi+h的殘差值，i=1，…，N(h)。

變異函數模型刻畫實驗變異函數值與滯后距的相關關系。球形模型是地質統計學中最常用的變異函數模型，本文選用球形模型進行計算。表達公式如下：

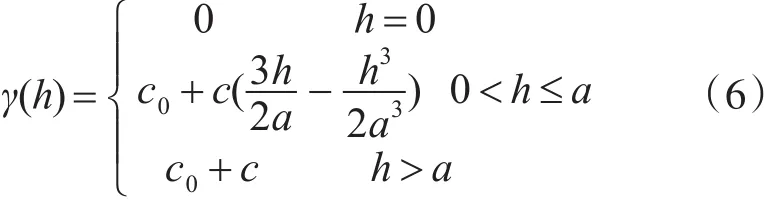
式中，c0是塊金值，c是基臺值，a是變程。

對式（6）分別關于ul和λi求導，并令其等于0，組成泛克里金算法的方程組。待插點的估計值正是通過解矩陣形式的方程組獲得的。

2.2 殘差分析基本原理

在統計學中，殘差是指在回歸分析中的實際觀察值與回歸估計值之差。可以理解，有多少對數據，就有多少個殘差。通過殘差所提供的信息，分析出數據的可靠性、周期性或其他干擾稱為殘差分析。

殘差分析的基本原理：殘差遵從正態分布N(δ，σ2)；δ與 σ 之比稱為標準化殘差，以 σ*表示；σ*遵從標準正態分布N(0，1)。若實驗點的標準化殘差落在置信區間以外的概率小于等于0.05，則稱可在95%置信區間將其判別為異常實驗點。

置信區間是指由樣本統計量所構造的總體參數的估計區間［17］，展現的是這個參數的真實值有一定概率落在測量結果的周圍的程度，其給出的是被測量參數的測量值的可信程度。通俗來講，置信區間反映的是一種規律，當不斷改變樣本的時候，有95%的機會，真實值落在置信區間里，而不僅僅局限在特定樣本。

在擬合趨勢函數部分，利用置信區間的殘差分析，可以幫助我們去掉預測值正確率小于0.05的樣本，增加趨勢函數的結構性和穩定性，以此達到提升插值效果的目的。這與泛克里金方法的適用條件是相一致的，即研究區域地質變量的變化有一定規律性，且可用簡單函數進行模擬。

2.3 泛克里金插值技術路線

插值的樣品數據是一系列已知具有某種屬性和三維空間坐標的點，這些三維屬性點來源于鉆孔上的樣品數據。整體建模流程分四步（圖1（左）），步驟二和三是為插值提供已知信息和目標信息，步驟三的實現是本文的研究重點，可以進一步劃分為5個步驟（圖1（右））。殘差分析應用在對趨勢函數的擬合上，趨勢函數的對R(x)的計算至關重要。

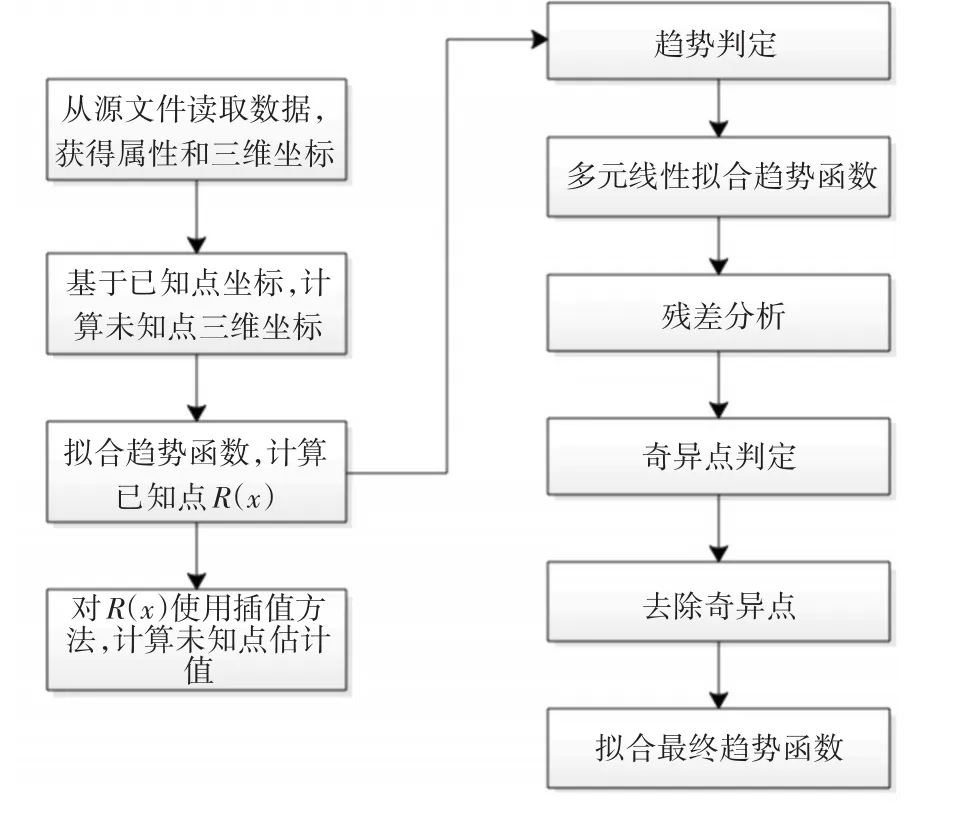
圖1 插值建模流程

3 基于殘差分析擬合趨勢函數

一般情況下，泛克里金插值方法的使用前提為數據滿足正態分布［3］。在地質中，數據滿足正態分布并不能代表數據在研究區具有一定的變化趨勢［14］，不代表可以用數學函數或模型對趨勢進行表達。由此，對于進滿足正態分布，但對趨勢函數沒有進行一定處理的泛克里金插值，其效果是不能保證的。

3.1 擬合趨勢函數

根據泛克里金方法的應用要求，實驗數據的空間分布必須滿足正態分布。因此，使用泛克里金方法的第一步是對數據進行正態分布檢驗。對實驗數據進行正態分析，在空間數據滿足正態分布的前提下，可基于泛克里金方法基本原理及變異函數擬合方法，對數據進行空間變異結構分析，繪制實驗變異函數曲線圖，并根據變異函數的理論模型擬合實驗變異函數。

趨勢函數表達研究變量與空間坐標的相關性的線性程度，趨勢函數的精度直接關系到R(x)的準確度。如果R(x)的計算結果不準確，插值結果將無意義。在多數情況下，地質變量的變化趨勢都可以用一階多元線性函數進行模擬［13］。本文選用一階多元線性函數對趨勢進行模擬。

3.2 對趨勢函數進行殘差分析

基于之前擬合出的趨勢函數，對實驗數據進行回歸分析，計算出所有點對數據的殘差和其對應的95%置信區間。用Matlab畫出殘差分析圖，奇異點的定義為置信區間不包含0的點。按照定義，將奇異點剔除。對剔除奇異點的實驗數據再次進行回歸分析，驗證奇異點已被剔除，實驗數據在95%的置信區間內符合趨勢函數。

3.3 插值準備

基于已知采樣點屬性值和擬合出的趨勢函數，按照式（3），計算出各采樣點的R(xi)。按照定義，R(x)為期望為0，協方差存在且平穩，且只依賴于兩點之間的相對距離，與絕對位置無關的變量。估計待插點的R*(x)，則要按照克里金插值的步驟。首先計算實驗變異函數值，量化數據間的相關關系，選擇變異函數模型，得到最終變異函數。具體步驟如下：

1）對得到的樣品數據進行空間性量化，根據空間位置坐標計算數據點對的歐氏距離；

2）按照距離對數據進行排序分組，計算每組的實驗變異函數值；

3）在h-γ*(h)圖（圖8）上標出各點 (h，γ*(h))，得到實驗變異函數大致走勢圖；

4）選取擬合相關系數較高的球行變異函數理論模型，應用線性規劃法求解變異函數模型中的各個參數；

5）推斷出一個統一的、由各向同性的結果表達式，得到最終的變異函數。

得到變異函數，便可計算協方差，進行泛克里金方程組求解，計算R*(x)的λi權系數。計算得到全部待插點的R*(x)，可按照式（3）得到全部待插點的估計值，以完成插值全過程。

4 實例驗證

本節對某油田解釋的測井數據進行孔隙度的泛克里金插值，共152口井，19508個采樣點，層厚95m，南北方向17772.38m，東西方向15230.5m。將采用本文方法進行插值的結果與未去奇異點的泛克里金方法的插值結果進行統計量對比和交叉驗證對比。

在實際建模中，首先建立結構模型，表達地質體表面的情況；生成網格模型；擬合趨勢函數，計算變異函數；求解泛克里金方程組，計算全部待插點的估計值（見圖2）。

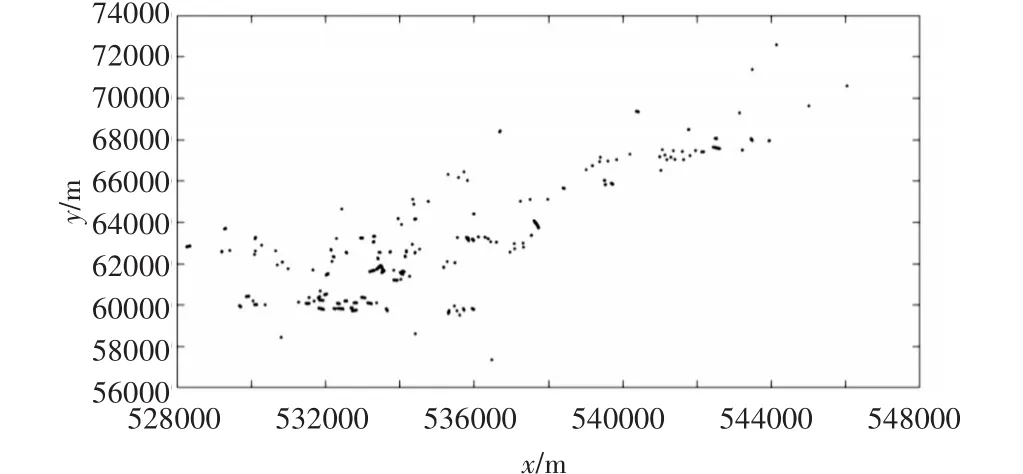
圖2 實驗數據平面分布圖

4.1 實驗數據檢驗

通過研究區孔隙度的統計特征分析結果（圖3），可以確定研究區的孔隙度數據符合正態分布，滿足泛克里金方法的應用要求。

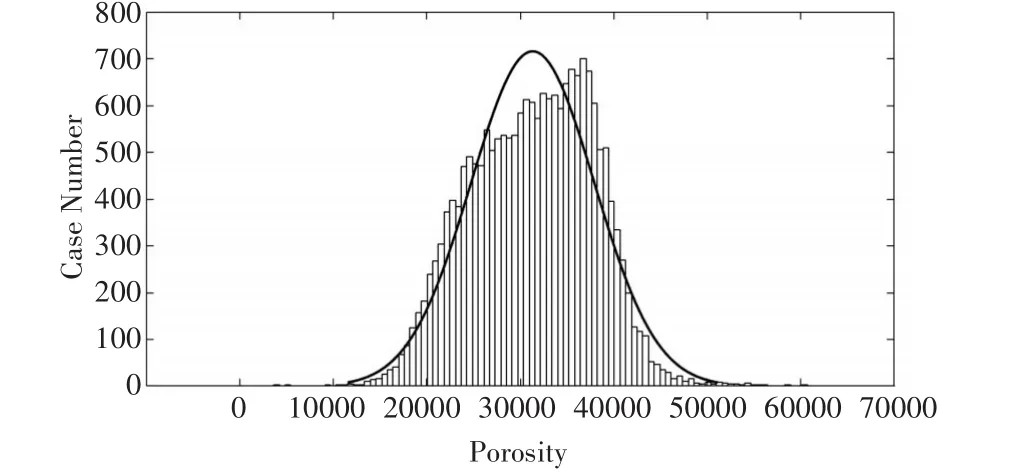
圖3 數據分析直方圖

4.2 擬合趨勢函數

本文使用多元線性函數進行擬合，得到擬合度為0.42的趨勢函數：

m(x，y，z)=-0.079x+0.21y+0.147z+9.39 （7）

對去除奇異點之后的實驗數據再次進行多元線性擬合趨勢函數，得到擬合度為0.74的趨勢函數：

m(x，y，z)=-0.081x+0.18y+0.14z+9.09 （8）

為驗證去奇異點效果，再次進行回歸分析，得到殘差分析結果（見圖5）。

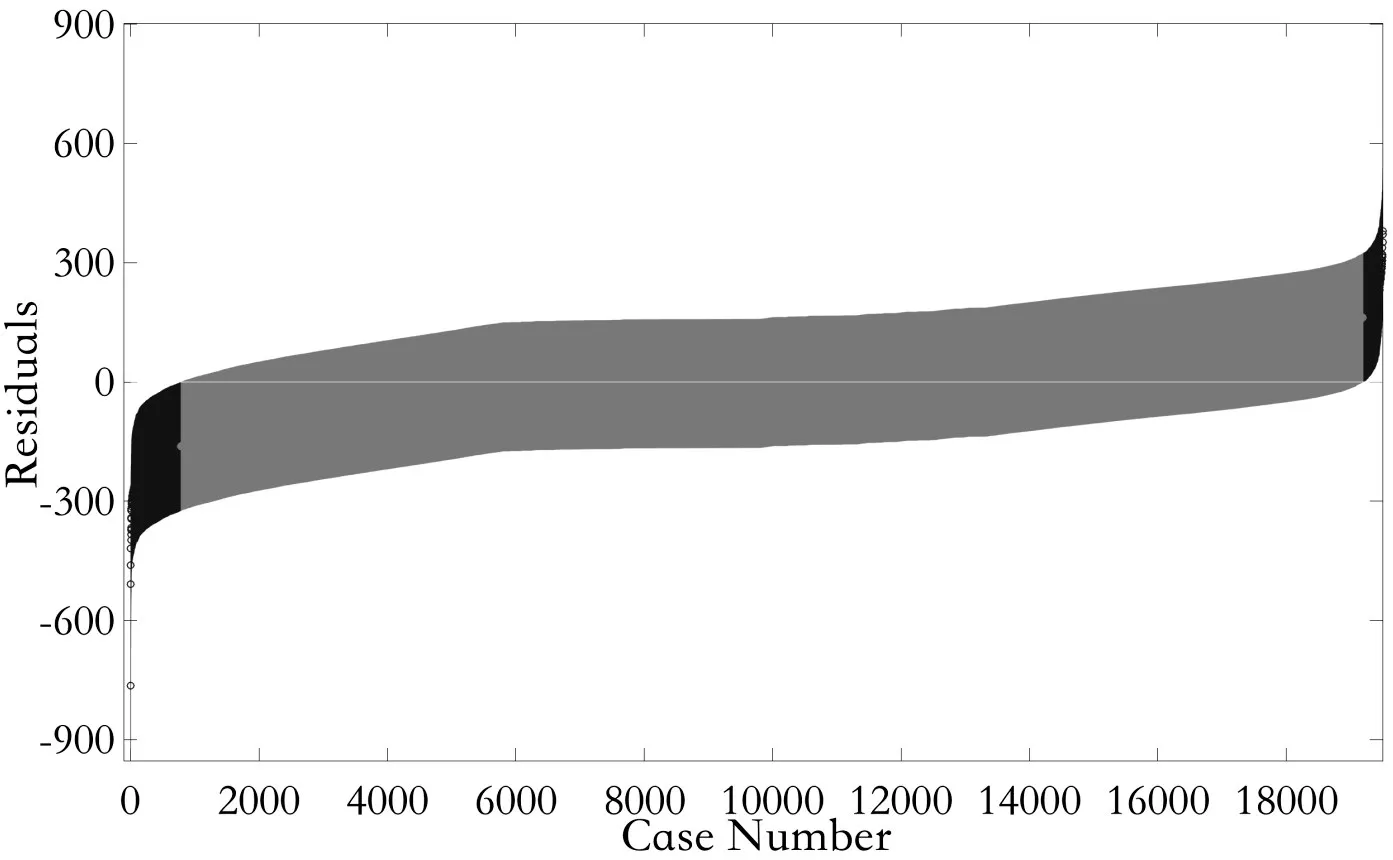
圖4 采樣數據殘差分析圖

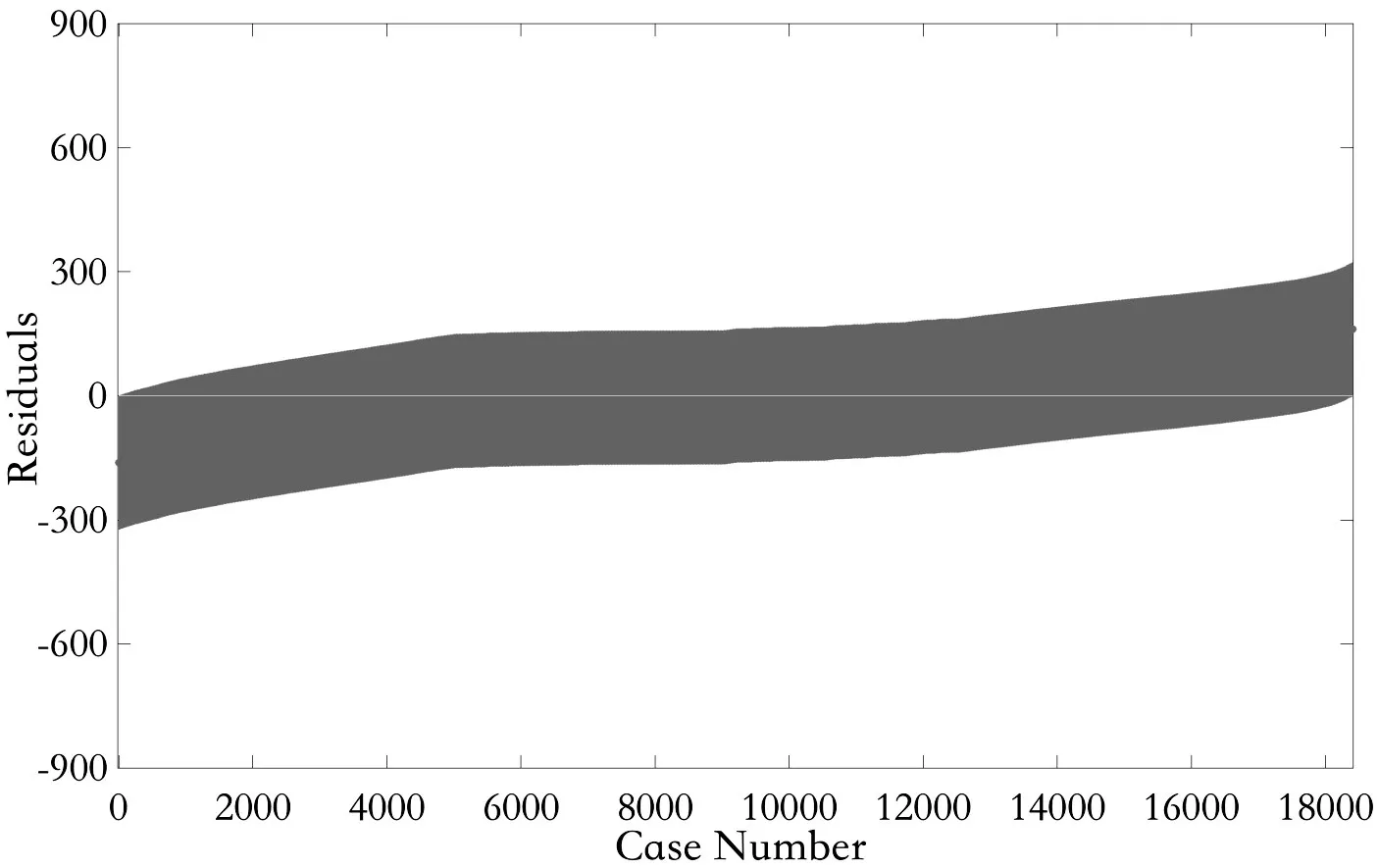
圖5 去奇異點殘差分析圖

4.3 變異函數擬合

本文選用球形模型來擬合變異函數，得到塊金值為2831.33，基臺值為9857.28，變程為1768.57。

4.4 插值計算

泛克里金插值方法的最后一步是計算插值結果，基于前文的各項計算和擬合出的函數，根據公式，計算得到待估點周圍相關樣品數據的權重值，并進行加權求和，計算出待估點的估計值。對全部待估點重復以上步驟，可以獲得全部待估點的屬性值，最終形成連續的三維地質屬性模型。

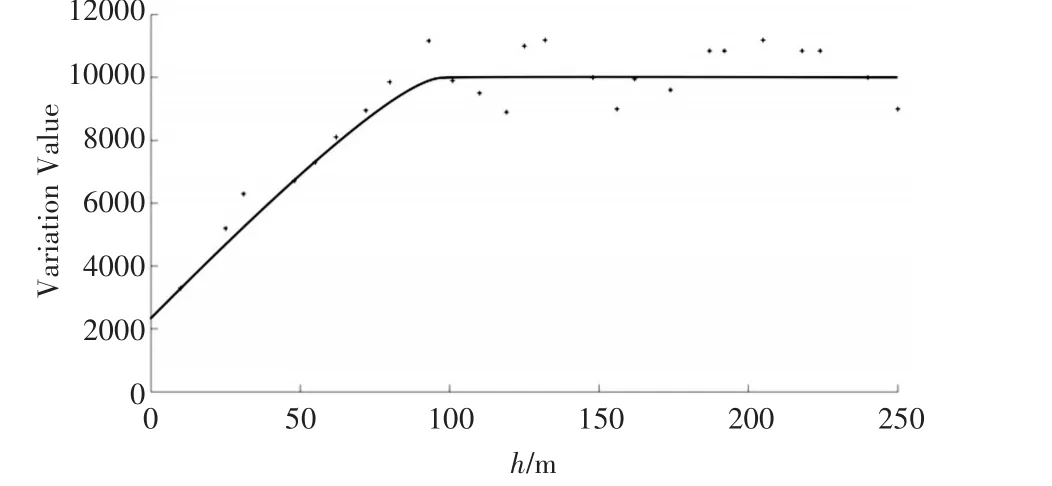
圖6 變異函數圖

4.5 結果與分析

4.5.1 統計量分析

比較統計量的方法表達數據的穩健性和分布情況是評價估計量好壞的基本方法［15］。T1、T2、T3分別是期望、方差和協方差。統計量如下：

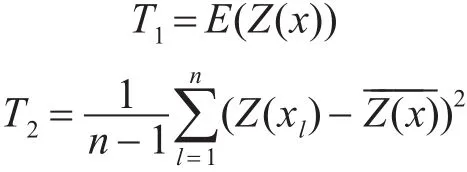
從期望和方差的角度出發，期望越接近真實值，無偏性越好，方差越小，有效性越好，協方差用于衡量兩個變量的總體誤差［18］。在此為比較采樣數據和本文方法的差異，以及采樣數據和未去奇異點的泛克里金方法的差異，分別計算以采樣數據為Z(xi)，以本文方法和泛克里金方法為Z(yi)的協方差。

由表1可知，由本文算法所得到的插值結果的統計量結果與采樣數據的期望較接近；相較于未去奇異點的克里金，本文方法的方差更小，且更接近于采樣數據方差，反應本文插值結果表達的地質變化規律更加平穩，與采樣數據反映的地質變化規律具有一致性。由此可證，去奇異點對插值效果的有效性是有意義的。

表1 統計量結果

4.5.2 交叉驗證

交叉驗證是指在插值過程中，去掉一個或一部分樣品點，對去掉的樣品點處進行插值，并將插值結果與樣品點處原有值進行對比，以驗證插值結果的準確性［18］。對本文方法和未去奇異點的泛克里金方法進行全部樣品數據的交叉驗證，結果為表2。可以看出，本文方法的均方誤差小于未去奇異點的交叉驗證結果。由此可知，本文方法具有更高的準確率。

表2 交叉驗證結果

5 結語

本文介紹了泛克里金和殘差分析的基本原理，并介紹了泛克里金插值的技術路線，并指出本文的研究意義在于提升整體泛克里金插值效果。本文利用測井解釋的孔隙度數據，對本文方法和未去奇異點的泛克里金插值方法進行分析，得出以下結論。

1）通過對實驗數據趨勢函數進行殘差分析，得到對實際地質變量變化規律更高精度的數學表達，為建立有效精確的三維地質屬性模型提供理論指導。

2）將本文方法應用到實際測井解釋的孔隙度數據，獲得合理有效的插值結果。將本文方法的插值結果與未去奇異點的泛克里金插值結果做統計量對比，結果表示本文方法插值結果的統計量結果更優，證明去奇異點對插值效果的有效性是有意義的。

3）對本文方法與未去奇異點的泛克里金插值結果進行交叉驗證，本文方法交叉驗證的結果的平均誤差和均方根誤差均小于未去奇異點的泛克里金，證明本文方法的插值效果的真實可靠性高于未去奇異點的泛克里金的插值效果。

4）研究得到的趨勢函數模擬方法適用于所有針對帶趨勢的地質建模方法，因此可以應用于礦產資源預測、儲層油氣預測與評價等多個地質領域。