基于粒子群優化的因子分解機算法
邱煜炎, 吳福生
蚌埠醫學院圖文信息中心, 安徽 蚌埠 233000
0 引言
近年來,云計算、大數據和移動互聯網技術發展迅速,網絡資源的信息量一直呈指數增長的趨勢,推薦系統作為解決信息過載和挖掘用戶潛在需求的技術手段得到普遍應用.推薦系統通過分析用戶與物品的關系行為,根據用戶偏好和相關屬性為其提供推薦列表,有效解決了信息過載問題[1].作為推薦系統的核心,機器學習算法的性能直接決定推薦質量.
線性回歸(linear regression,LR)[2]模型具有可解釋性、較強的泛化能力以及簡單快速求解的特點,是機器學習領域的基本算法.然而,在訓練過程中只有當輸入數據特征具有明顯的線性關系時,才能表現出較好的建模效果.并且,線性模型本身缺乏對輸入特征間關系的探索機制,它只考慮了每個特征對結果的單獨影響,而沒有考慮特征間的組合對結果的影響.
因子分解機(factoration machine,FM)[3,4]作為一種新式通用的機器學習算法,其設計思想來自矩陣分解和線性回歸模型.因子分解機在對特征建模時,不僅考慮線性回歸算法中單個特征對模型的影響,而且考慮特征間的相互關系,以構建二階線性模型.FM模型適合高維稀疏的數據集,學界基于此模型也做了廣泛研究[5]和應用[6].
粒子群優化(Particle Swarm Optimization,PSO)[7,8]是一種群體隨機優化算法技術,其最初目的是生動模擬鳥群優雅而又難以預測的隊形設計.作為一種全局優化技術,PSO的特點是不要求被優化函數具有可微可導連續等性質,而且能夠達到快速收斂的效果[9].
盡管FM模型對于稀疏型數據集有較好的表現,但是在樣本量較小的情況下,梯度下降方法不能保證參數收斂到全局最優解[10].針對以上問題,本文提出一種基于粒子群優化的因子分解機算法(particle swarm optimization factorization machine,PSO-FM).首先運用PSO算法快速獲得全局最優區域,然后利用FM模型的梯度下降算法進行精確求解,最后在醫療診斷數據集Diabetes上進行驗證.實驗結果表明,相對于FM算法,PSO-FM算法在模型訓練速度和測試集準確度上都有較好的表現.
1 因子分解機
1.1 線性模型
線性模型包含線性回歸、邏輯回歸等,其特點是只包含若干個特征對結果的單獨影響,而沒有考慮特征間相互組合對結果的影響.對于一個含有n維特征的模型,線性回歸形式如下:
(1)
其中,(ω0,ω1,ω2,...,ωn)為模型參數,(x1,x2,...,xn)為數據特征.從(1)式可以看出,模型來自各個特征獨立的計算結果,并沒有考慮特征之間的相互關系.然而,組合特征在一定程度上具有意義,比如“美國”與“感恩節”,“中國”與“春節”,這兩組特征組合,同時出現會表現出更強的購買意愿,而單獨考慮國家及節日是沒有意義的.
1.2 二項式模型
在(1)式的基礎上,考慮任意2個特征分量之間的關系,可得以下模型
(2)
模型涉及參數的數量為
(3)
對于一次項參數ωi的訓練,只要樣本對應的xi不為0,即可完成一次訓練.然而對于二次項參數ωij,需要樣本xi和xj同時不為0,才可以完成一次訓練.對于數據稀疏的實際應用場景,二次項參數ωij訓練非常困難,xi和xj同時不為0的樣本非常稀少,這會導致ωij不能得到足夠的訓練,從而導致模型準確度不高.
1.3 因子分解機
為解決上述由于數據稀疏引起訓練不足的問題,為每個特征維度引入一個輔助向量
Vi=(vi1,vi2,vi3,...,vik)T∈Rki=1,2,...,n
(4)
其中,k(k∈N+)是輔助變量的維度,屬于超參數,一般k< (5) 由于W不方便求解,因此引入隱變量V (6) 并令 VVT=W (7) 理論研究表明[11]:當k足夠大時,對于任意正定的實矩陣W∈Rn×k,均存在實矩陣V∈Rn×k,使得W=VVT.假設樣本中有n個特征,每個特征對應的隱變量維度為k,則參數個數為1+n+nk.在線性模型的基礎上,利用隱變量替代二次項系數矩陣,得出以下模型 (8) (9) 最終得出,時間復雜度為O(kn)的表達式 (10) 對于機器學習問題,基于梯度優化的參數更新表達式如下 (11) (12) (13) 結合公式(11)~公式(13),得參數的優化公式 (14) 如果針對回歸問題,其偏導數為 (15) 如果針對二分類問題,其偏導數為 (16) 上述二分類問題使用對數損失函數進行求解,公式(16)中的σ表示為躍階函數Sigmoid: (17) 作為一種進化計算技術,粒子群優化PSO算法源于對鳥群捕食的行為研究.鳥群通過種群交流以及自身經驗調整個體搜尋路徑,從而搜尋捕食最優位置[12].其中每只鳥的位置/路徑則是自變量的組合,每次到達的地點的食物密度即函數值.每次搜尋都會根據自身經驗(自身歷史搜尋的最優地點pbest)和種群交流(種群歷史搜尋的最優地點gbest,gbest是pbest中的最好值)調整自身搜尋的方向和速度,從而找到最優解[13].相對于其他優化算法,PSO算法的優勢在于簡單容易實現并且沒有許多參數的調節. PSO算法適用于連續函數極值問題的求解,流程如圖1所示 圖1 粒子群優化算法流程 根據流程,PSO算法中所涉及的參數有:(1) 種群數量:粒子群算法的最大特點就是速度快,因此初始種群取值50~1 000皆可;(2) 迭代次數:取值范圍100~4 000,要在時間耗費和搜索廣度進行權衡;(3) 慣性權重:取值范圍0.5~1,該參數反映了個體歷史成績對現在的影響;(4) 學習因子:取值范圍0~4,分為個體和群體兩種學習因子;(5) 空間維數:粒子搜索空間維數,即代表自變量的個數;(6) 位置限制:限制搜索空間范圍,即代表自變量的取值范圍;(7) 速度限制:設置合理的粒子速度可以防止速度過快導致的跳過最優解位置以及速度過慢導致的收斂速度慢的問題. PSO算法首先初始化一組隨機解,然后利用反復迭代搜索出最優解.每次迭代后,粒子通過對比兩個極值(pbest和gbest)來更新自己的參數[14].當粒子確定最優位置后,更新粒子的速度和位置,公式如下 Vi=ω×Vi+c1×rand()×(pbesti-xi)+c2×rand() ×(gbesti-xi) (18) xi=xi+Vi (19) 公式(18)、公式(19)中,i=1,2,...,N,N是此群中的粒子總數,vi是粒子的速度,xi是粒子所在當前位置,ω是上次更新速度的慣性因子,rand()是隨機數(范圍0~1之間),c1和c2代表學習因子. 根據公式(14),對于少量數據集,利用梯度下降方法對FM進行參數求解容易陷入局部最優解.為此,本文提出了基于粒子群優化的因子分解機算法(PSO-FM),利用粒子群算法全局搜索能力求解因子分解機模型參數. PSO-FM算法融合了PSO全局搜索能力以及FM局部梯度求解精度能力的優勢.首先采取PSO算法確定優化區域,然后利用基于公式(14)的梯度方法提升參數精度,以達到全局搜索,加速尋優的目的. (20) 對于二分類問題,需要添加Sigmoid函數進行映射.在利用PSO算法求解時,首先需要構建粒子群P={p1,p2,...,pm},即包含m個粒子群,每個粒子pi按照公式(20)可以表示為 pi={ω0,ω1,ω2,...,ωn,υ1,1,υ1,2,...,υ1,k,...,υn,1,υn,2,...,υn,k} (21) 每個粒子pi代表PSO模型的參數向量即速度,該向量的維度為D=1+n+n×k. 根據公式(18)利用粒子群優化算法進行參數求解過程中,采用錯誤率作為適應度函數 (22) 其中,#error表示正確個數,#all表示所有訓練樣本個數.當PSO算法適應度收斂到一定閾值[15],則利用公式(14)對參數進行梯度求解. 根據以上描述,PSO-FM算法的目的就是通過公式(20)快速獲取全局最優區域,然后在區域內利用公式(14)進行梯度求解,以此達到全局最優.具體算法步驟如下: Step 1:設置超參數,包括粒子規模m,慣性權重ω,優化參數c1、,設置公式(14)中的η和λ,隱變量維度k,迭代次數i,PSO適應度閾值r1和FM模型交叉熵損失函數閾值r2; Step 2:初始化每個粒子參數,即粒子的速度和位置; Step 3:根據公式(22)計算單個粒子適應度; Step 4:對單個粒子當前適應度與該粒子時間軸上最佳適應度pbest進行對比,如果優于pbest,則對pbest進行更新; Step 5:將粒子群中的各個粒子當前適應度,與整個群體最佳適應度gbest進行對比,如果某粒子優于gbest,則對gbest進行更新; Step 6:根據公式(18)和公式(19)更新每個粒子的位置和速度;當適應度小于閾值r1,保存當前粒子參數向量,執行Step 7;當適應度大于閾值r1,反復執行Step 3; Step 7:利用公式(14)進行梯度計算; Step 8:當滿足迭代次數i或者損失函數值小于r2,返回最優參數向量Xbest; Step 9:根據Xbest構建FM模型,用于待測試數據進行預測. 本實驗針對二分類問題對PSO-FM模型算法進行驗證,選取醫療診斷數據集Diabetes,并與傳統的FM算法進行對比.Diabetes數據集包含786條數據,特征個數為8,分類結果為是否有糖尿病({0,1}).按實驗要求,將數據集按4∶1的比例分為614條訓練集和154條測試集. 實驗算法采用Python 3.6編寫的代碼,硬件環境采用Pentinum(R) G4400-3.3 GHz處理器,8 G內存.根據本文3.3算法步驟,Step 1超參數設置如表1所示. FM算法的運行參數如表2所示. 表1中的超參數已在本文3.3中說明,不做贅述.表2中參數根據公式(14),η表示學習率,λ表示正 表1 PSO-FM運行超參數Tab.1 PSO-FM running hyperparameters 則化參數,k表示隱向量維度,i表示迭代次數[16]. 為驗證PSO-FM算法能否在短時間內收斂并獲得滿意精度,圖2對比了PSO-FM模型與FM模型在訓練集根據公式(17)所得損失函數值的變化情況. 表2 FM運行超參數Tab.2 FM running hyperparameters 圖2 算法對數損失函數迭代對比 由圖2可以看出,PSO-FM算法在同樣的迭代次數內,對數損失函數值一直優于FM算法.表3列出兩種算法訓練時間(TraingTime,TT)以及在訓練集的準確率(TrainingAccuracy,TRA)和測試集上的準確率(TestingAccuracy,TEA)指標. 從表3的結果可以看出,PSO-FM算法訓練時間明顯短于傳統的FM算法,而且無論在訓練集還是測試集,其準確性都要優于后者.本實驗數據集具有訓練樣本量少、屬性參數多的特點,對于傳統的基于梯度的FM算法很容易陷入局部最優.憑借PSO算法全局搜索能力,并結合梯度下降求解參數,PSO-FM算法對于復雜參數尋優問題表現出更強的數據建模效果. 表3 算法運行指標Tab.3 Algorithm operation index 本文利用PSO算法引入FM模型中,在全局快速搜索的前提下進行基于梯度參數的求解方法.通過在數據集Diabetes上進行實驗,結果表明,相對于傳統的FM模型,PSO-FM模型表現出更快的模型訓練速度,以及更高的模型預測準確率.本文中的PSO-FM基于前人經驗,使用統一的超參數,基于實驗數據量比較小的情況,種群規模和迭代次數設置都比較小.在以后的實驗中,可以考慮使用網格搜索(Grid search)方法,基于不同的數據集發掘出表現能力更強的超參數配置值.后續的研究工作中,將針對大規模多維度數據,解決PSO-FM算法應對單機計算時內存溢出問題以及針對該算法設計多機并行計算問題.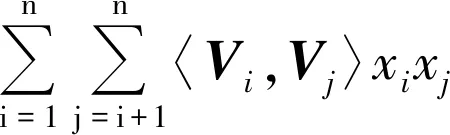
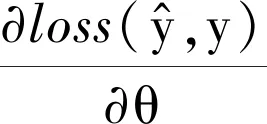
2 粒子群優化算法
2.1 算法描述
2.2 算法流程
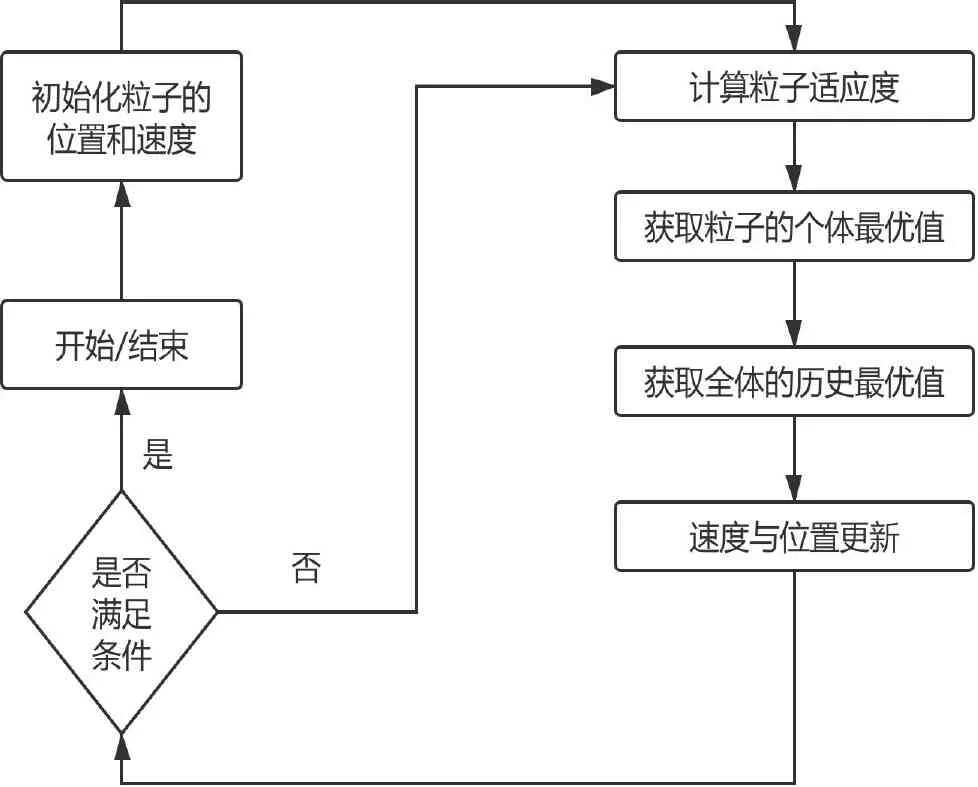
Fig.1 Particle swarm optimization algorithm flow2.3 算法規則與公式
3 基于粒子群優化的因子分解機算法
3.1 PSO-FM算法思路
3.2 PSO-FM算法模型
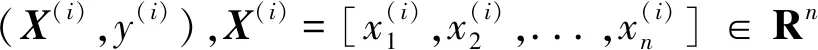
3.3 算法步驟
4 實驗與結果分析
4.1 實驗準備

4.2 結果及分析

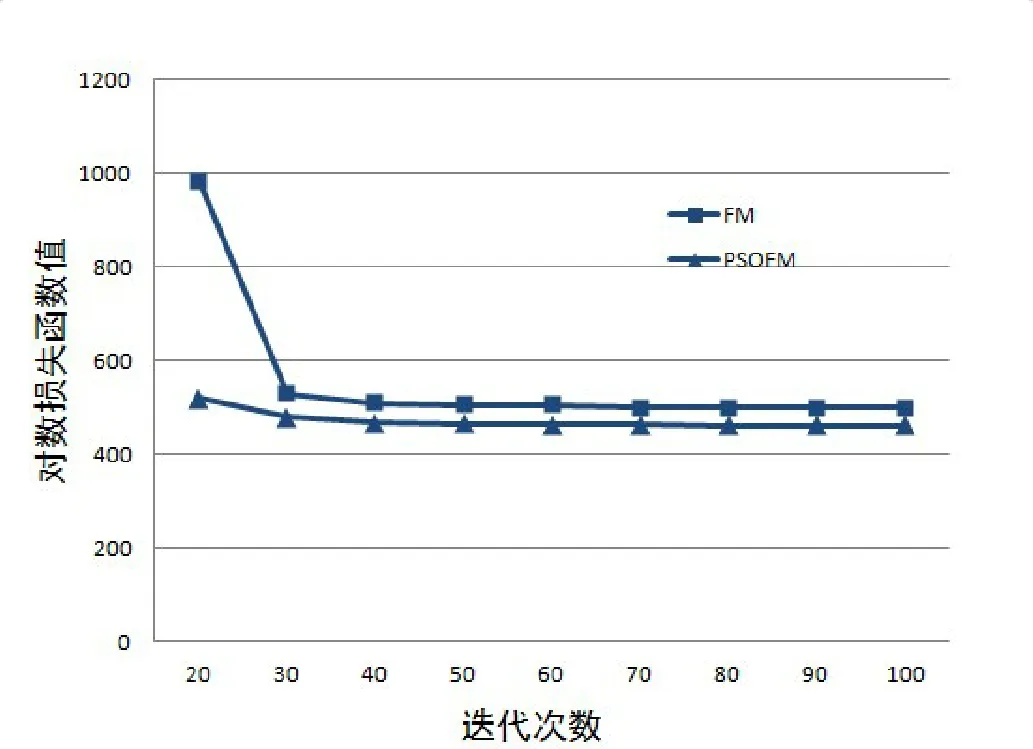
Fig.2 Iterative comparison of algorithm logarithmic loss function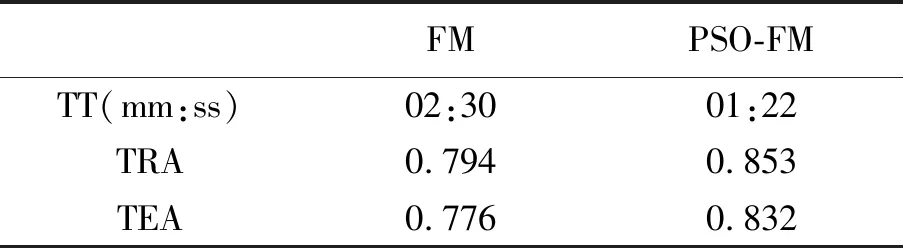
5 總結

