Lorenz系統與Rossler系統在限定時間內的滑模同步控制
蔣楠, 魏毅強
1.山西廣播電視大學公共基礎學院, 山西 太原 030027;2.太原理工大學數學學院, 山西 太原 030001
0 引言
混沌系統具有內隨機性、分維性、普適性及標度性等特征,并且對初始條件、參數變化具有較強的敏感性和隨機性,使得混沌系統的同步控制在保密通信、生物工程、信息信號處理及其他領域得到了廣泛應用,同時實現混沌同步的諸多有效方法也相繼提出,比如:非線性反饋控制法[1,2]、自適應控制法[3,4]、滑模變結構控制法[5]、模糊同步控制法[6]等.近幾年,混沌系統的滑模同步已經成為非線性領域研究的熱門課題.由于滑模控制對外界擾動具有較強的魯棒性和較好的動態性能,受到了學者們廣泛的關注.文獻[7]通過設計切換函數和控制率,實現了多個分數階混沌系統的滑模同步;文獻[8]研究了一類分數階參數不確定混沌系統的滑模同步;文獻[9]通過結合分數階運算和整數階同步控制方法,設計了一種同步控制器,實現分數階混沌系統的同步.在實際應用中,系統無法避免地受到外界干擾、非線性輸入、參數未知等多種因素的影響,針對系統的這些影響因素,學者們提出了多種解決方法.文獻[10]針對帶有外部擾動項和不確定性的分數階混沌系統,運用自適應模糊滑模控制方法實現了系統的投影同步;文獻[11]在未知參數和外部擾動的情況下,選取分數階積分滑模面,實現了混沌系統的局部漸近穩定;文獻[12]通過設計分數階積分滑模面,在外界干擾和系統不確定的情況下,實現了兩個分數階混沌系統的同步.上述文獻大部分只考慮了外界干擾、系統不確定、非線性輸入等因素對系統的影響,卻忽略了系統達到同步的時間,而在實際應用中,混沌系統在限定時間內達到同步更具有實際價值和現實意義.
本文構造了一個新的滑模面,通過比較系統同步誤差沿著兩個滑模面收斂到原點的時間,證明新的滑模面比傳統滑模面的收斂速度更快,以含有外界干擾項的混沌系統為研究對象,根據Lyapunov穩定性理論和滑模控制方法,在滑模控制律的作用下,使得同步誤差收斂到原點,實現了Lorenz系統與Rossler系統在限定時間內的異結構同步.最后通過數值仿真驗證了結論的正確性和有效性.
1 系統模型
選取Lorenz系統為驅動系統
(1)
可將驅動系統改寫為如下矩陣形式
(2)
f(x)F(x)θ
因此驅動系統可以表示為
(3)
其中,x(t)為系統的狀態變量;f(x)為連續的非線性函數;矩陣F(x)中的元素為連續的非線性函數;θ為參數向量;dm為外部擾動.
選取Rossler系統為響應系統
(4)
可將響應系統改寫為如下矩陣形式
(5)
g(x)G(x)φ
因此驅動系統可以表示為
(6)

(7)
即
(8)

(9)

則系統(9)在有限時間內穩定,且T滿足
引理2[14]對于狀態變量x,若初始條件x0>0,滿足下列條件
則狀態變量x在有限時間內穩定,且時間T滿足
2 滑模控制律設計與穩定性分析
2.1 滑模控制律設計
文獻[13,15]中的傳統滑模面為
(10)
此滑模運動存在的充要條件為
(11)
由此得到誤差系統為
(12)
設計新的滑模面為

(13)
滑模運動存在的充要條件為
(14)
由此得到誤差系統為

(15)
定理1 如果誤差系統的初值ei(0)
證明 分別根據引理1和引理2,收斂時間為
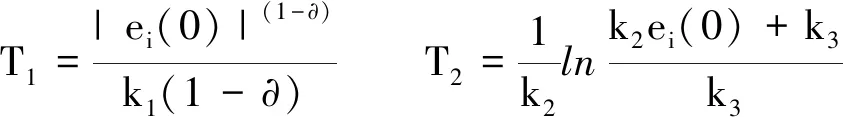


當ei(0) 當k1=k3時,T0 根據自適應控制理論和滑模控制理論,結合所設計的新的滑模面(13),將滑模控制律設為 (16) (17) 定理2 針對混沌同步誤差系統(8),選取滑模面(13),在滑模控制律(16)作用下,系統在限定時間 (18) 內收斂到滑模面. 證明 根據Lyapunov穩定性理論,選擇Lyapunov函數為 (19) 對(19)式求導得到 (20) 將(14)式代入 (21) 將(8)式與(17)式代入 (22) 代入得 放縮可得 將(16)式代入 為了驗證本文所提理論結果的可行性和有效性,以Lorenz系統(1)為驅動系統,Rossler系統(4)為響應系統進行Matlab數值仿真.利用設計的滑模控制律,在系統含有外界干擾項的情況下,實現在限定時間內兩個異結構混沌系統的滑模同步.同步誤差系統(8)可以表示為如下形式: 圖1 切換滑模面 圖2 同步誤差沿滑模面(13)隨時間的變化Fig.2 Time history of synchronized error along the sliding surface(13)圖3 同步誤差沿滑模面(10)隨時間的變化Fig.3 Time history of synchronized error along the sliding surface(10) 基于Lyapunov穩定性理論和滑模控制方法,構造了新的滑模面,設計了滑模控制律,實現了含有外界干擾項的Lorenz混沌系統與Rossler混沌系統在限定時間內的滑模同步,并用數學推理證明了新的滑模面比傳統滑模面具有更快的的收斂速度.最后,系統仿真結果表明,本文所提出的理論結果具有正確性和有效性.

2.2 穩定性分析



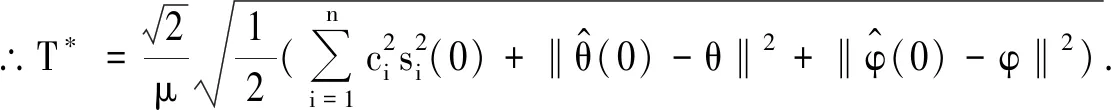
3 數值仿真

Fig.1 Switch the sliding surface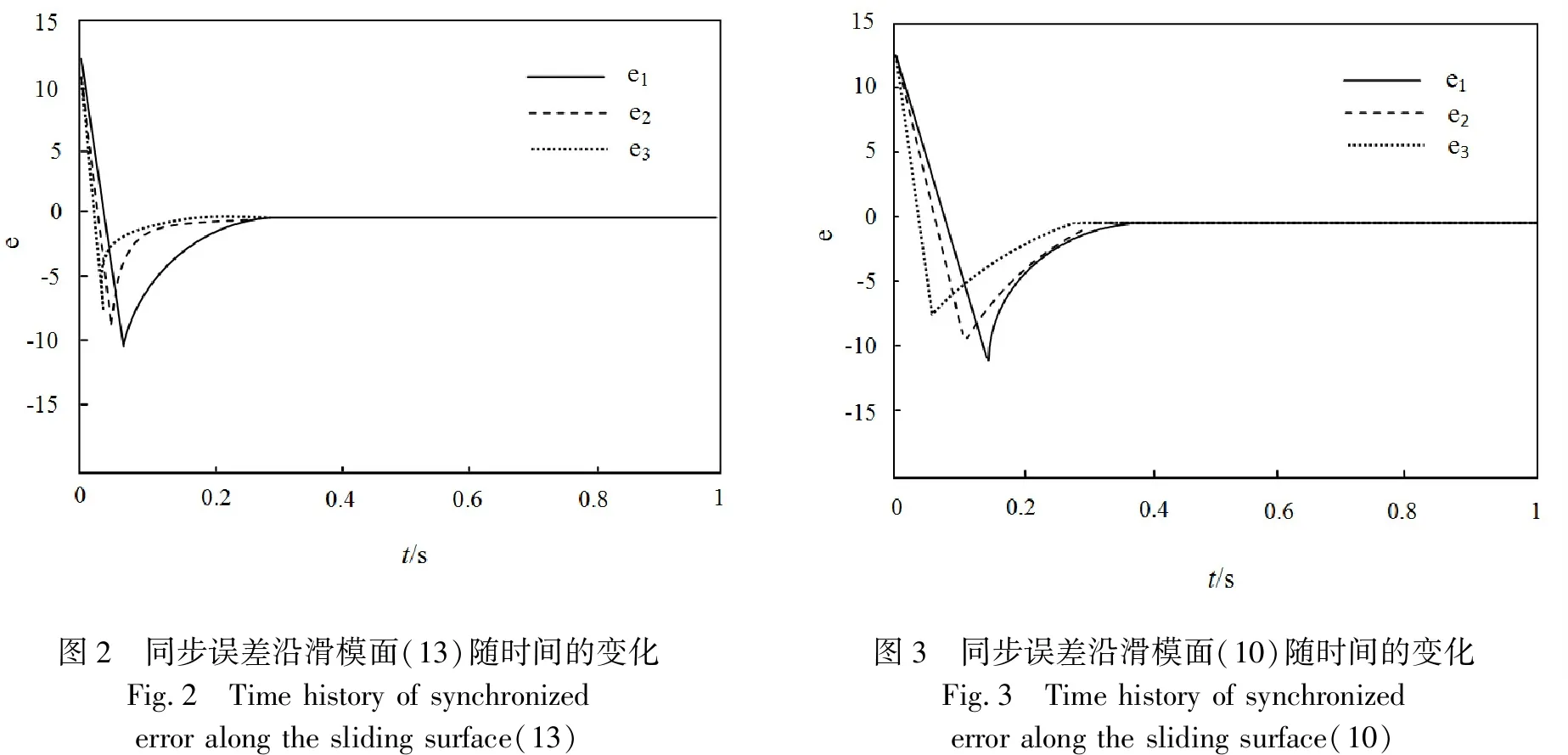
4 結論

