一種抗噪的移動時間勢能聚類算法

陸慎濤,葛洪偉

(江南大學 a.江蘇省模式識別與計算智能工程實驗室; b.物聯網工程學院,江蘇 無錫 214122)

0 概述

聚類算法是一種無監督的學習方法,其遵循一定的規則將數據分成若干個類別,滿足同一類別數據盡可能相似、不同類別數據盡量相異的原則,并在不同領域聚類分析都作出了重要貢獻,如模式識別[1]、生物信息[2-3]、大數據分析[4]等。當前聚類分析引起了研究人員的關注,并提出多種典型的聚類算法,如基于劃分的聚類算法(K-means[5-6]、K-medoids[7]等)、基于層次的聚類算法(Chameleon[8]、Cure[9]等)、基于密度的聚類算法(DBSCAN[10]、DPC等)和基于網格的聚類方法聚類算法(STING[11]、WAVECLUSTER[12]等)。這些聚類算法雖然有著較好的聚類效果,但大部分算法對含噪聲復雜的數據集的聚類效果較差,影響算法的實際應用。

文獻[13]提出一種移動時間層次聚類算法TTHC,該算法按照數據點本身的勢能和數據點與父節點的相似度構建邊緣加權樹,依照提前設置的類簇中心個數使用層次聚類得到結果。由于TTHC算法采用了全新的基于移動時間的相似性度量準則,相對于傳統的聚類方法,TTHC算法具有高效便捷的特點,可取得較優的聚類結果與聚類精度。但TTHC算法對數據集進行聚類時,無法識別出數據集中存在的噪聲數據點,聚類結果容易受到噪聲數據的影響。

本文提出一種抗噪的移動時間勢能聚類算法(APCTT)。該算法依照相似度來尋找各數據點的父節點,從而獲得各數據點和父節點之間的距離,并按照該距離以及數據點本身的勢能值得到λ值,根據λ值遞增曲線找到數據集中的噪聲點,并聚到一個新類簇,對去除噪聲點后的數據集根據數據點和父節點之間的距離進行層次聚類以獲得聚類結果。

1 移動時間層次聚類算法及其缺陷分析

1.1 TTHC算法

TTHC算法是基于勢能的聚類來計算各數據點的勢能值。數據點之間的勢能Φij定義如下:

(1)

其中,rij為點i與點j的歐氏距離,δ是用來防止發生rij為零。minDi是點i到其他各點的最小距離,其與δ的計算方式如式(2)、式(3)所示:

minDi=minrij≠0,j=1,2,…,N(rij)

(2)

δ=mean(minDi)/S

(3)

其中,N是數據點個數,S是比例因子,設置為1,mean是求平均值的函數。在得到每兩個點之間的勢能Φij后,那么數據點的勢能Φi定義如下:

(4)

遵照牛頓運動定律,質點間引力大小如下:

Fij=|Φi-Φj|/rij

(5)

質點的加速度如下:

(6)

因此,質點從數據點i移動到數據點j所需時間如下:

(7)

數據點i和數據點j的相似度定義如下:

(8)

父節點的定義如下:

(9)

其中,Si為數據點i和父節點parent[i]的相似度,那么Si的定義如下:

Si=Si,parent[i]

(10)

1.2 TTHC算法缺陷分析

TTHC算法雖然方便快捷,但是并不能識別一些數據集中存在的噪聲數據點,即無法處理這些噪聲數據點,因此對這些數據集進行聚類后的結果也不準確。

如圖1(a)所示的數據集,深色點是噪聲數據點,采用TTHC算法聚類后獲得的結果如圖1(b)所示。從圖1(b)可以看出,使用TTHC算法進行聚類后獲得的結果和原始數據集有著較大誤差,很多數據點都被分配了錯誤的類別,這是由于TTHC算法不能識別數據集中的噪聲數據點,影響到了TTHC算法的聚類效果與精度。因此,如何使算法自適應地識別數據集中的噪聲數據,并對噪聲數據點處理后的數據集進行聚類,是進一步研究分析的內容。

圖1 缺陷分析示例

2 APCTT算法

2.1 噪聲點識別

APCTT算法首先定義λ值,λ值是數據點與父節點的距離和數據點的勢能的絕對值的比值,通過構造λ值的遞增曲線來識別數據集中的噪聲數據點。定義1即數據點是否為噪聲數據的考量指標。通過分析可以發現,噪聲數據點的勢能值往往比正常數據點的勢能值大,并且噪聲數據點到父節點的距離也比正常數據點到父節點的距離大。因此,噪聲數據點的λ值和正常數據點的λ值差異明顯,可以根據λ值來識別噪聲數據點和正常數據點。

定義1λi是數據點與父節點之間的距離和數據點勢能的絕對值的比值,如式(11)所示:

λi=ρi/|Φi|=ρi/(-Φi)

(11)

在式(11)中,由于數據點的勢能都是負值,因此數據點的勢能的絕對值等于勢能的相反數。在一般情況下,數據集中的噪聲數據點的數量遠遠少于正常數據點,而且噪聲數據點的分布比較稀疏,所以它們的勢能值都比較大,又由于勢能恒為負值,因此它們勢能的絕對值比較小,此外這些噪聲數據點和父節點的距離也比較大,但是數據集中的非噪聲數據點分布較之噪聲數據點會更密集,因此其勢能比噪聲數據點勢能要小得多。噪聲點判定示意圖如圖2所示。

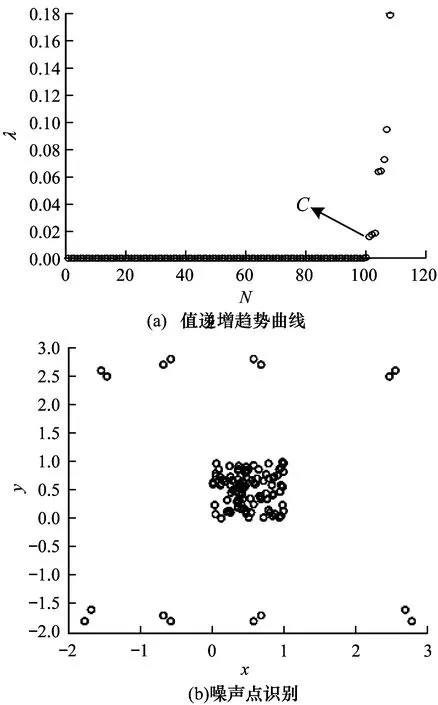
圖2 噪聲點判定示意圖

因為勢能等于負值,所以非噪聲數據點的勢能的絕對值就比較大,和數據集中的噪聲數據點相比,這些非噪聲數據點和父節點的距離也相對較小。通過繪制數據點的λ值遞增曲線,可以在λ值的遞增曲線上發現,噪聲數據點和正常數據點之間存在一個拐點,圖2(a)中的點C即為數據集的拐點,遞增曲線上位于拐點前面的數據點為正常數據點,遞增曲線上位于拐點后面的數據點為噪聲數據點,圖2(b)為對數據集識別噪聲數據后的結果,其中,分布在圖中上下的圓點是數據集被識別出來的噪聲數據點。從圖2(a)和圖2(b)可以看出,通過在λ值遞增曲線上尋找拐點,從而通過找到λ值的遞增曲線上的拐點識別出數據集中的噪聲數據點這一方法是可行的。識別出數據集中的噪聲數據點后,對分離出噪聲數據點之后的數據集進行下一步算法處理。

2.2 算法描述

數據點之間的相似度基于質點在數據點間的移動時間得到,然后基于數據點之間的相似度來尋找父節點。根據每個數據點與其父節點的距離來生成邊緣加權樹,再基于此邊緣加權樹采用層次聚類的方法來取得聚類結果,其中邊緣加權樹中的權值即為數據點與父節點的距離,采用層次聚類之后再取得聚類結果。APCTT算法步驟描述如下:

步驟1按照式(1)～式(10)計算各數據點勢能值與數據點之間的相似度,依據相似度尋找各數據點的父節點,再計算數據點到其父節點的距離。

步驟2根據式(11)計算各個數據點的λ值,按照λ值大小繪制遞增曲線,尋找遞增曲線中的拐點,通過曲線的拐點來完成噪聲數據的識別。

步驟3將識別出的噪聲數據聚到一個新的類簇。

步驟4對分離出噪聲數據后的數據集根據數據點與父節點的距離作層次聚類,獲得聚類結果。

2.3 算法時間復雜度分析

APCTT算法的時間復雜度由計算勢能與相似度以及距離、對λ值進行升序排序、基于數據點到父節點的距離使用層次聚類三部分構成。假定有n個數據點,那么對數據點之間的距離與相似度和數據點勢能的計算需要的時間復雜度是O(n2),對λ值作升序排序所需的時間復雜度是O(n2),對去除噪聲數據點后的數據集進行層次聚類所需的時間復雜度是O(n2),所以APCTT算法所需的時間復雜度是O(n2)。由于TTHC算法的時間復雜度是O(n2),結合以上分析,相對于原始的TTHC算法,APCTT算法的時間復雜度未增加。

3 實驗結果與分析

3.1 實驗結果評價指標

本文實驗中采取FM[14]、F1-measure[15]和ARI[16]3個評價指標對實驗結果作分析。3個評價指標都是位于0～1之間,數值均是越靠近1表示聚類的效果越佳,越靠近0表示聚類的效果越差。

3.2 結果分析

在合成數據集及UCI[17]真實數據集上與各算法作對比實驗來檢驗APCTT算法的性能。算法中使用的距離都默認為歐式距離。

3.2.1 合成數據集的聚類結果分析

表1中的DS1數據集是由4組隨機數構成,都是服從正態分布并且期望值都等于0,第1組的數據點個數是200個,標準差為2,中心是(0,0);第2組的數據點個數為200個,中心為(16,11);第3組的數據點個數為400個,標準差為3,中心為(6,13);第4組的數據點個數為800個,標準差為4,中心為(12,0)。DS2數據集是3組服從標準正態分布的隨機數,3個中心數據點分別是(0,0)、(3,5)和(6,0),每一組都是有300個數據。DS1數據集和DS2數據集都是不含噪聲數據點的。2two2d+n、flame+n是對無噪聲數據的數據集添加噪聲點后的數據集。運用CSPV算法[18]、PHA算法[19]、TTHC算法和APCTT算法對合成數據集作聚類實驗。

表1 合成數據集

圖3和圖4分別是4種算法在各數據集上實驗的聚類結果。表2～表4分別是對不同的數據集使用各算法進行實驗所得的3個聚類評價指標值。從圖3、圖4可以看出,對于DS1和2two2d+n數據集,APCTT算法具有較優的實驗結果。從圖4(a)、圖4(b)和圖4(c)可以看出,CSPV算法、PHA算法和TTHC算法不能識別出數據集中的噪聲數據點,而從圖4(d)可以明顯看出,APCTT算法準確地識別出了數據集中的噪聲數據點,從而能夠提高算法的聚類效果。表2～表4表明,APCTT算法在DS1、DS2、2two2d+n和flame+n數據集上,3個聚類評價指標都高于或者等于TTHC算法。此外,在2two2d+n和flame+n數據集上,APCTT算法可以識別出噪聲數據點并且把其歸入一個新的類簇,而TTHC算法并不能識別出噪聲點。

圖3 不同算法在DS1合成數據集上的聚類結果

Fig.3 Clustering effects of different algorithms on DS1 synthetic datasets

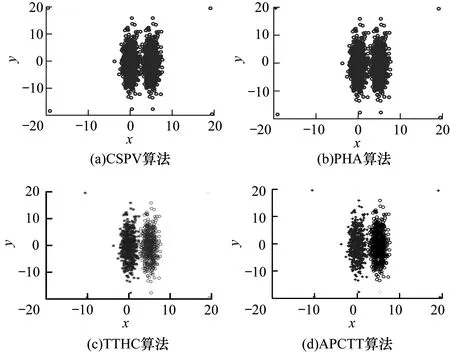
圖4 不同算法在2two2d+n合成數據集上的聚類結果

Fig.4 Clustering effects of different algorithms on 2two2d +nsynthetic datasets

表2 4種算法在合成數據集上的FM值

表3 4種算法在合成數據集上的ARI值

表4 4種算法在合成數據集上的F1-measure值

Table 4 F1-measure values of four algorithms on synthetic datasets

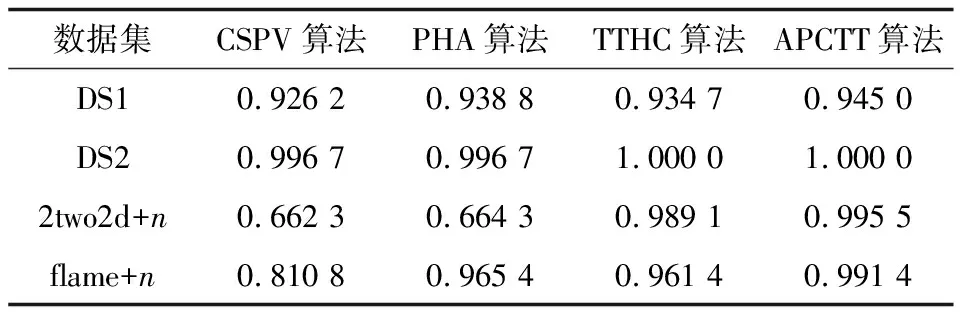
數據集CSPV算法PHA算法TTHC算法APCTT算法DS10.92620.93880.93470.9450DS20.99670.99671.00001.00002two2d+n0.66230.66430.98910.9955flame+n0.81080.96540.96140.9914

從表2～表4可以看出,在DS1、DS2、2two2d+n和flame+n數據集上,APCTT算法的3個評價指標都比PHA算法高,而且APCTT算法能夠識別出噪聲點,所以聚類結果更好,但是PHA算法由于無法識別噪聲數據,導致聚類結果要比APCTT算法差。在DS1、DS2、2two2d+n和flame+n數據集上,APCTT算法的3個評價指標均比CSPV算法高,由于CSPV算法在對數據集聚類時未考慮到數據集中存在的噪聲點并去識別,因此導致聚類效果會變差。根據上述分析,相對于TTHC算法不能識別數據集中的噪聲數據,且聚類結果容易被噪聲數據影響,APCTT算法不但可以識別噪聲數據點,而且將噪聲點歸入一個新的類簇之后可以獲得更好的聚類結果。

3.2.2 UCI數據集的聚類結果分析

使用不同算法對UCI數據集(見表5)進行聚類實驗,檢驗APCTT算法的性能,得到的實驗結果如表6～表8所示。

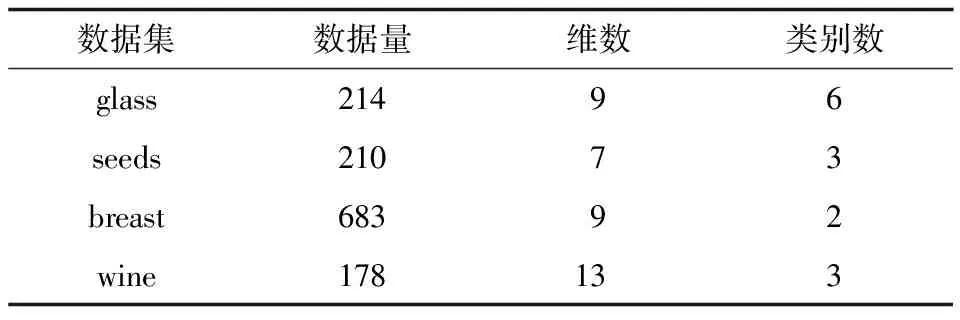
表5 真實數據集

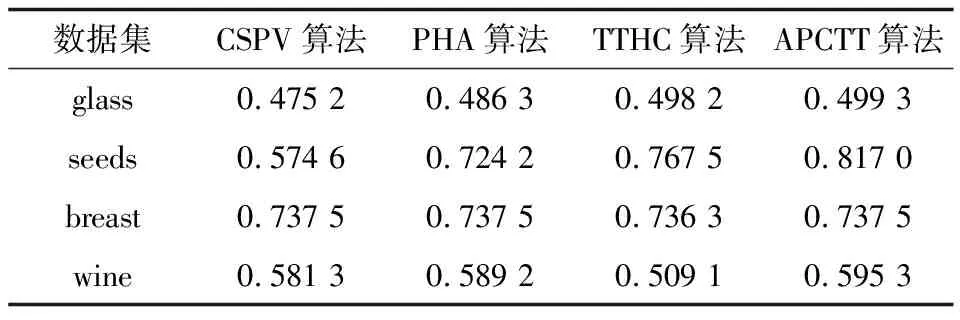
表6 真實數據集FM值

表7 真實數據集ARI值

表8 真實數據集F1-measure值

從表6～表8可以看出,對于glass、seeds、breast和wine數據集,APCTT算法的FM值、ARI值以及F1-measure值都比TTHC算法高。在glass、seeds和wine數據集上,APCTT算法的3個評價指標值都比CSPV算法高。在breast數據集上,APCTT算法的ARI值和F1-measure值都比CSPV算法高,FM值等于CSPV算法。針對glass、seeds和wine數據集,APCTT算法的FM值、ARI值和F1-measure值都比PHA算法高。在breast數據集上,APCTT算法的ARI值和F1-measure值都比PHA算法高,FM值等于PHA算法。

總體來說,APCTT算法在真實數據集上的聚類效果優于TTHC算法、PHA算法和CSPV算法。這是由于APCTT算法能夠自動識別真實數據集中存在的噪聲數據點然后將這些噪聲點區分出來,并歸到一個新類簇中,再對區分出噪聲數據后的數據集作進行聚類,能夠提高聚類效果。

4 結束語

針對TTHC算法無法識別出數據集中存在的噪聲數據點,導致算法聚類效果較差的缺陷,本文提出一種抗噪的移動時間勢能聚類算法APCTT。該算法將歐氏距離作為度量,在低維度的數據集上可以取得較好的聚類效果。實驗結果表明,與原始TTHC算法相比,APCTT算法的FM值、ARI值以及F1-measure值均有明顯提高。如何使APCTT算法在處理高維度數據集時,尋找更加有效的距離度量方法來取得較好的聚類效果將是下一步的研究內容。