無雙線性對的部分盲代理重簽名方案

牛淑芬,李文婷,王彩芬

(西北師范大學 計算機科學與工程學院,蘭州 730070)

0 概述

自代理重簽名的概念被提出以來[1],研究者相繼設計了多種代理重簽名方案[2-4]。代理重簽名的特點主要體現為代理者可將用戶(受托者)的簽名轉換成另一用戶(委托者)的簽名,在不獲取兩方用戶私鑰的同時實現簽名轉換。此特性使其在現有的網絡環境下能夠應用于數字版權管理系統、簡化證書管理及跨域身份認證等方面[5-7]。由于基于身份的公鑰密碼體制[8]可減輕用戶對證書的依賴,因此結合兩者優勢,基于身份的代理重簽名既能解決繁瑣的密鑰管理問題,又能滿足在簽名轉換過程中對私鑰的保護。

SHAO等人于2007年首次提出基于身份的代理重簽名方案[9]。2009年,HU等人在強q-SDH困難問題假設下提出基于身份的代理重簽名方案[10]。2014年,馮婕等人利用目標抗碰撞哈希函數提出一種基于身份強不可偽造的代理重簽名方案[11]。2015年,TIAN等人構造了格上基于身份的代理重簽名方案,用于抵抗量子攻擊。2018年,WANG等人利用二次剩余理論提出一種基于身份的代理重簽名方案[13]。由于代理者能夠獲得所轉換的消息,因此使用者需要在代理重簽名中添加盲性。為保證代理者的權益不被濫用,YANG等人于2018年提出部分盲代理重簽名體制[14],并構造了可證明安全的簽名方案。

在以上研究中,同類代理重簽名中基于身份的密碼體制存在運算開銷大不利于實際應用的問題,且缺少部分盲性,不能對簽名者隱匿待簽消息內容,從而造成消息泄露。本文在文獻[13]方案的基礎上,基于大整數分解困難問題,提出一個單向、單用基于身份的部分盲代理重簽名方案,以解決使用雙線性對運算開銷較大這一問題,并通過部分盲性避免惡意簽名濫用。

1 基礎知識

大整數分解困難問題為:給定一個合數N滿足N=pq,p和q是兩個大素數,要求輸出p或q。

大整數分解假設為:設l是一個安全參數,N為一個合數滿足N=pq,p和q是兩個l比特的大素數。如果不存在概率多項式時間的敵手tT以不可忽略的概率εR分解合數N,則稱(tT,εR)大整數分解假設成立。

2 形式化定義及安全模型

定義1無雙線性對的基于身份的部分盲代理重簽名方案由以下9個算法組成:

1)Setup(1λ)→(par,msk):輸入安全參數λ,運行系統參數生成算法輸出公開參數par和系統主密鑰msk。

2)Extract(par,msk,ID)→sk:輸入par、msk和用戶身份信息ID,PKG運行密鑰提取算法輸出公私鑰對(pk,sk)。

3)Rekey(skA,skB)→rkA→B:輸入Alice(受托者)和Bob(委托者)的私鑰skA和skB,PKG運行重簽名密鑰產生算法輸出重簽名密鑰rkA→B。

4)Agree(par)→c:輸入par,受托者Alice與代理者Proxy運行協商消息算法生成一個公共消息c。

5)Sign(par,sk,m,c)→(h,σ):輸入par、c、消息m和受托者私鑰sk,由受托者產生原始簽名σ。

6)Blind(h,c,σA,k,pkA)→(h′,σ′A):輸入c、消息摘要h、原始簽名σA、盲化因子k和受托者公鑰pkA,受托者運行盲化算法輸出盲化的消息摘要h′和盲化的原始簽名σ′A,并發送給代理者。

7)ReSign(rkA→B,c,h′,σ′A,pkA)→σ′B:輸入rkA→B、c、h′、σ′A和pkA,代理者首先驗證σ′A的合法性,若不合法,輸出⊥;否則,代理者運行重簽名生成算法輸出與委托者公鑰pkB對應的部分盲代理重簽名σ′B,并發送給受托者。

8)Unblind(σ′B,k,pkB)→σB:輸入部分盲代理重簽名σ′B、盲化因子k和委托者公鑰pkB,受托者首先驗證σ′B的合法性,若不合法,輸出⊥;否則,受托者運行脫盲算法輸出代理重簽名σB。

9)Verify(m,c,pk,σ)→{0,1}:輸入消息m、公共消息c、對應的公鑰pk和簽名σ,若關于消息m和公共消息c的簽名σ對應于公鑰pk合法,驗證者接受簽名,輸出1;否則,輸出0。

新方案的安全性分別由存在性不可偽造性和部分盲性構成。存在性不可偽造性在新方案中要求不存在一個外部敵手能夠偽造一個新消息的代理重簽名。下面先以敵手A與挑戰者C的交互游戲來定義方案的存在性不可偽造性。

1)系統建立。挑戰者C運行Setup算法獲得系統參數par、系統主公鑰mpk和系統主密鑰msk,挑戰者將mpk及系統參數發送給敵手,保密msk。

2)詢問。敵手A能夠自適應地向挑戰者C進行以下詢問:

(1)密鑰提取詢問。當敵手A提交身份ID的密鑰提取詢問時,挑戰者C運行Extract算法輸出skID并返回給敵手A。

(2)重簽名密鑰詢問。當敵手A提交(IDA,IDB)的重簽名密鑰詢問時,挑戰者C首先對身份IDB進行密鑰提取詢問來獲得skIDB,然后C運行Rekey算法輸出重簽名密鑰rkA→B并返回給敵手A。

(3)簽名詢問。A與C運行Agree算法產生公共消息c,當敵手A提交(ID,m,c)的簽名詢問時,挑戰者C首先對身份ID進行密鑰提取詢問來獲得skID,然后C運行算法輸出原始簽名sig并返回給敵手A。

(4)重簽名詢問。當敵手A提交(sig′A,h′,c,IDA,IDB)的重簽名詢問時,挑戰者C首先驗證盲化的sig′A是否為對應于pkA關于盲化消息摘要h′和c的合法簽名,若不合法,輸出⊥;否則,C對(IDA,IDB)進行重簽名密鑰詢問獲得rkA→B,然后運行Resign算法輸出部分盲代理重簽名sig′B。假設攻擊者A在Blind算法中選擇k為盲化因子,A最后運行Unblind算法輸出(h,c)的重簽名。

3)偽造。敵手A輸出偽造的簽名(sig*,m*,c*,ID*),若滿足以下條件,敵手A贏得這個游戲:(1)Verify(sig*,m*,c*,ID*)=1;(2)A沒有進行過ID*的密鑰提取詢問;(3)A沒有進行過(ID*,m*)的簽名詢問;(4)A沒有進行過(sigi,h'*,ci,IDi,ID*)的重簽名詢問,IDi表示任一用戶,sigi表示任何一個簽名。

定義2若敵手A在以上游戲中攻擊成功的概率是可忽略的,則稱新的部分盲代理重簽名方案在適應性選擇消息攻擊下是存在性不可偽造的。

部分盲性在新方案中是指代理者不能夠將最終的代理重簽名與部分盲代理重簽名相對應。參考已有的部分盲簽名方案的安全定義[16-17],下面將通過敵手B與挑戰者D的游戲來定義新方案的部分盲性。

1)系統建立。挑戰者D運行Setup算法、Extract算法和Rekey算法,產生系統參數par、受托者和委托者的密鑰對(skA,pkA)和(skB,pkB)以及重簽名密鑰rkA→B,發送par和rkA→B給敵手B。

2)準備。敵手B選擇兩個長度相等可區分的消息m0和m1,以及公共消息c發送給挑戰者D。

3)詢問。挑戰者D隨機選取b∈{0,1},對消息(m0,c)和(m1,c)運行Blind算法,得到盲化的消息摘要與盲化的消息簽名(h′b,c,σ′A,b)和(h′b-1,c,σ′A,b-1)發送給敵手B進行重簽名。B收到(h′b,c,σ′A,b)和(h′b-1,c,σ′A,b-1)后運行ReSign算法得到部分盲代理重簽名σ′B,b和σ′B,b-1并返回給挑戰者D。D收到簽名σ′B,b和σ′B,b-1后運行Unblind算法進行脫盲得到最終重簽名σB,b和σB,b-1,并將(mb,c,σB,b)和(mb-1,c,σB,b-1)返回給敵手B。

4)應答。B輸出對b的猜測b′,若b=b′,則B贏得了游戲。

B在上述游戲中獲勝的優勢定義為:

Adv(B)=|2Pr[b=b′]-1|

定義3若敵手B在以上游戲中攻擊成功的概率是可忽略的,則稱新的部分盲代理重簽名方案具有部分盲性。

3 具體方案

本文基于WANG等人方案[13]設計了一個無雙線性對的基于身份的部分盲代理重簽名方案,具體算法如下[18]:

2)Extract算法。輸入系統參數par、系統主密鑰msk和用戶身份信息ID,PKG運行密鑰提取算法計算用戶私鑰sk=H(ID)dmodN和pk=H(ID)modN,得到公鑰/私鑰對(sk,pk)。

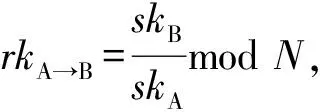
4)Agree算法。受托者Alice與代理者Proxy協商一個公共消息c。

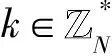
7)ReSign算法。輸入rkA→B、c、h′、sig′A和受托者的公鑰pkA,代理者首先驗證(σ′A)2=Rc·pkh′A是否成立,若不成立,輸出⊥;否則,代理者計算σ′B=rkA→B·σ′A,最后輸出部分盲代理重簽名sig′B=(σ′B,R,IDB)發送給受托者。

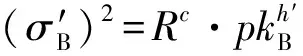
9)Verify算法。輸入消息m、公共消息c、對應的公鑰pk和簽名σ,驗證者驗證等式σ2=Rc·pkh是否成立,若成立,驗證者接受簽名,輸出1;否則,輸出0。

4 安全性證明與效率分析

4.1 正確性證明

本文方案的正確性證明如下:

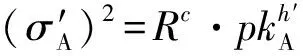
Rc·H(IDA)d·2h·H(IDA)2k=

Rc·H(IDA)h·H(IDA)2k=

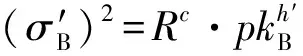
4.2 不可偽造性證明

證明假設存在一個敵手A能夠以不可忽略的概率偽造簽名,下面將構造一個算法C作為挑戰者與敵手A進行交互游戲,回答A的哈希詢問、密鑰提取詢問、重簽名密鑰詢問、簽名詢問和重簽名詢問,從而解決因子分解問題。具體詢問過程如下:

1)系統建立。挑戰者C運行Setup算法獲得系統參數par、系統主公鑰mpk和系統主密鑰msk,將mpk及系統參數發送給敵手,保密msk。

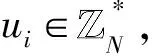
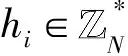
4)密鑰提取詢問。挑戰者C收到敵手A關于身份IDi的密鑰提取詢問時,C首先查找Hlist列表中是否有(IDi,ui,pki)的項,若存在,則返回u給A;否則重新進行H()詢問獲得(IDi,ui,pki)的項并添加至列表Hlist,將ui作為回答返回給敵手A。

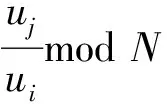
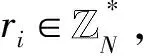
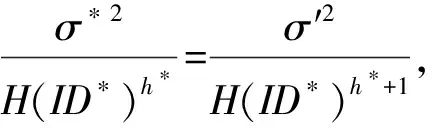
4.3 部分盲性證明

定理4本文提出的部分盲代理重簽名方案具有部分盲性。

證明敵手B的目的是要將最終的重簽名與部分盲代理重簽名相對應,所以,本文假設挑戰者D擁有任一用戶的私鑰并且能夠產生原始簽名,B擁有重簽名密鑰。下面將以挑戰者D與敵手B的交互游戲來證明。

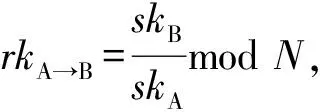
2)準備。敵手B選擇兩個長度相等可區分的消息m0和m1,以及公共消息c發送給挑戰者D。

4)應答。B輸出對b的猜測b′。

4.4 效率分析

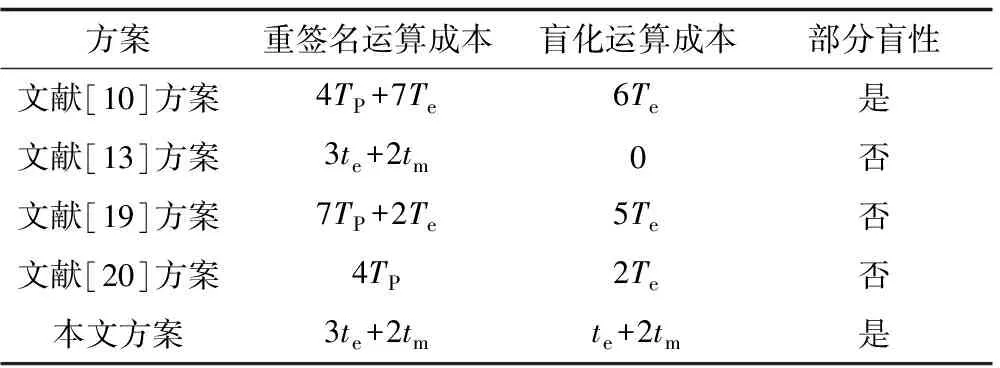
表1 運算效率比較

由表1可以看出:文獻[19]的方案使用了7次雙線性對與2次指數運算,使得一般設備難以負擔其計算開銷,因此,與本文方案相比實用性較差;文獻[10]方案雖然增加了部分盲性,但同樣存在計算開銷大影響實際應用;文獻[20]方案存在的安全漏洞為不能抵御受托者的重簽名偽造攻擊,本文依據給出的安全模型及證明保證了方案的不可偽造性;與文獻[13]的方案相比,本文方案在重簽名階段計算效率持平的前提下,增加了部分盲的特性,能夠保護受托者的隱私并且保證了代理者的權利不被濫用,可用性更強。

5 結束語

為解決現有部分盲代理重簽名方案計算成本高與證書管理難的問題,本文提出一種建立在大整數分解困難問題上基于身份的部分盲代理重簽名方案,通過避免使用雙線性對提高了計算效率。本文方案在隨機預言模型下滿足正確性、不可偽造性和部分盲性,效率分析結果也表明了其性能優勢。本文方案不滿足雙向、多用的特性,在應用中具有一定程度的局限性,因此,下一步工作將在此方面對方案進行改進。