基于螺旋式電容傳感器的生物質含水量測量

李云龍， 燕德國， 鄧永強， 張文彪， 韓曉娟

（1.大唐長山熱電廠， 吉林 松原 138000； 2.華北電力大學 控制科學與計算機工程學院， 北京 102206）

0 引言

生物質能源因其可再生以及碳中性的特點，在我國能源系統(tǒng)中占據(jù)著越來越重要的地位[1]，[2]。生物質燃料的特性分析是生物質能源利用過程的重要參考依據(jù)。 在生物質燃料發(fā)電過程中，生物質燃料的含水量不僅影響電廠機組的發(fā)電效率，還影響電廠生產過程的安全性，因此，對生物質燃料含水量的快速測量具有十分重要的意義。

目前，已有多種技術相對成熟的生物質含水量的測量方法被應用于各個領域。 總的來說，這些方法主要分為兩大類，即直接法和間接法[3]～[5]。直接法包括干燥法和化學法，這類方法具有原理簡單、測量精度較高和不易受外界環(huán)境影響的優(yōu)點，但是，也具有破壞性較大和耗時較長的缺點，不適合大規(guī)模使用，通常是在實驗室環(huán)境下完成的，因此，這類方法常被作為獲取標準值的參考方法。 間接法包括電學法、電磁法、近紅外光譜法（NIR）和X 射線法等，間接法一般具有操作簡單、快速、破壞性小和重復性好等優(yōu)點，但是，測量精度易受外部環(huán)境和樣本特性的影響，須要進行不斷的改進和優(yōu)化[6]。

電學法作為間接法的一個主要分支，在生物質含水量測量方面得到了一定的應用。 Mizukami Y 基于電阻和電容值估計了茶葉的含水量， 并開發(fā)了一個同時含有阻抗和電容的新模型， 該模型的測量精度較高，但是，容易受到葉片成熟度的影響[7]。Solar M 為了無損測定榛子的含水量，分析了電容、 介電常數(shù)等8 種電學參數(shù)隨榛子含水量的變化趨勢， 根據(jù)逐步多元回歸分析建立的計算模型實現(xiàn)了榛子含水量的高精度預測， 該方法不須要破壞榛子的結構，具有成本低和非侵入的優(yōu)點[8]。Kandala C V 通過測量平行板電容器在兩個頻率下的電容和相角，得出了一個經驗方程，并以此來估計糧食作物的含水量，該方法具有檢測速度快、測量精度高和樣本可以重復使用的優(yōu)點， 但是只適用于小樣本[9]。當待測樣品的含水量分布得不均勻時，單一電容傳感器只能求得含水量的平均值，并不能提供關于樣品含水量不均勻性的任何信息[10]～[12]。 上述研究都是基于普通的平行板電容器，由于平行板電容器的“邊緣效應”，會導致傳感器的靈敏度下降和非線性增強， 影響最終的測量精度。因此，如何獲得更精確的測量結果還須進一步研究。

本文將采用一種螺旋結構的電容傳感器 （簡稱螺旋式電容傳感器） 對生物質的含水量進行測量。相比于平行板電容器，螺旋式電容傳感器的靈敏度分布均勻，被廣泛應用于過程參數(shù)的檢測，而且該種傳感器還可以克服生物質水分分布不均勻的問題[13]～[15]。 本文首先利用有限元方法對螺旋式電容傳感器的結構進行優(yōu)化，然后根據(jù)優(yōu)化結果搭建相應的測量系統(tǒng)，最后對測量系統(tǒng)的準確性進行驗證。 本文提出的螺旋式電容傳感器可以實現(xiàn)生物質含水量的快速準確測量，將為生物質燃料的高效安全利用提供保障。

1 生物質含水量的測量

在實際應用過程中，平行板電容器會由于“邊緣效應”導致傳感器的靈敏度均勻性下降和非線性增加。 螺旋式電容傳感器由不同角度的平行板電容疊加而成，其靈敏度均勻性有較為明顯的改善。 通過對螺旋式電容傳感器的結構參數(shù)進行優(yōu)化，可以有效減小由于生物質堆積情況不同和生物質水分分布不均對測量結果造成的影響。

1.1 測量原理

隨著生物質含水量（MC）的變化，樣本的介電常數(shù)會發(fā)生相應改變， 從而引起傳感器的電容（C）發(fā)生變化；建立生物質含水量與電容的數(shù)學模型后，就可以通過對生物質電容的測量實現(xiàn)對生物質含水量的預測。

1.2 傳感器的結構

螺旋式電容傳感器的結構如圖1 所示。 從圖1 可以看出， 傳感器主要由檢測極板和激勵極板構成，為減小電磁干擾和提高靈敏度，傳感器兩端設置了兩個環(huán)形的屏蔽接地電極。

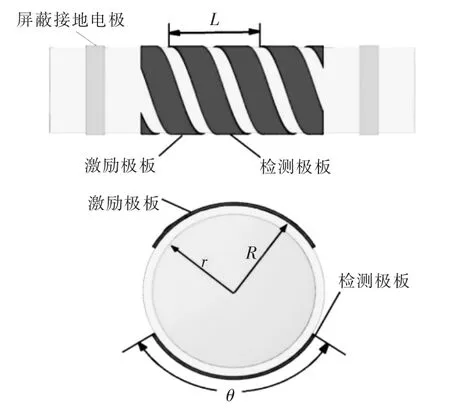
圖1 螺旋式電容傳感器的結構Fig.1 Structure of the helical capacitance sensor

圖1 中：θ 為傳感器極板的張角；r 和 R 分別為管道內徑和外徑。 極板在管道上的旋轉角度也是一個很重要的參數(shù)，用極板旋轉一周（360°）的軸向長度L 來表征。 本文所用管道的r=23 mm，R=25 mm。為了確定傳感器的結構，本文主要優(yōu)化極板張角θ、 極板旋轉一周的軸向長度L 和極板旋轉的圈數(shù)s。 為了方便研究，將每個待優(yōu)化的參數(shù)均分為 4 個水平進行實驗：θ 分別為 90，110，130，150 °；L 分 別 為 0.1，0.15，0.2，0.3 m；s分別為 1，1.25，1.5，1.75。

1.3 優(yōu)化指標

本文基于有限元方法對不同結構傳感器的靈敏度分布進行優(yōu)化， 將測量區(qū)域分割成很多小單元，通過對每個單元建立公式進行求解，從而得到整個區(qū)域的解。 傳感器靈敏度的計算式為

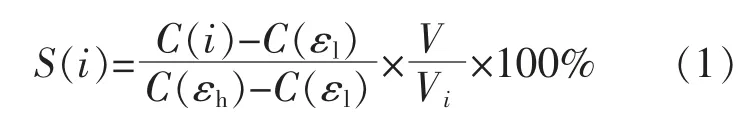
式中：S（i）為傳感器的靈敏度；C（i）為 傳 感 器 的電容，F(xiàn)；C（εl）為測量區(qū)域的介質全為空氣時，傳感器的電容，F(xiàn)；C（εh）為測量區(qū)域的介質全為水時， 傳感器的電容，F(xiàn)；V 和Vi分別為整個測量區(qū)域和第i 個區(qū)域的體積，m3。

為了方便描述傳感器靈敏度的均勻性， 將Sr作為表征傳感器靈敏度分布均勻性的指標，Sr越小，傳感器的靈敏度分布越均勻。

式中：Sσ為每個測量區(qū)域靈敏度的標準差；為測量單元的靈敏度的平均值。

1.4 仿真優(yōu)化結果

采用正交試驗設計的方法對螺旋式電容傳感器的結構進行優(yōu)化。 通過正交性從全面試驗中挑選出部分有代表性的點進行正交試驗， 從而以盡量少的試驗， 獲得足夠多的有效信息。 基于COMSOL 軟件對螺旋式電容傳感器的結構進行建模仿真。 在激勵極板上施加1 V 的電壓，通過求解檢測極板表面的電荷量進而求得電容。 正交試驗的設計及結果見表1。 從表1 中可以看出，第8組參數(shù)所對應的Sr最小， 即對應的傳感器的靈敏度均勻性最好。 因此，將 θ=110 °，L=0.3 m，s=1.25 作為最終的優(yōu)化結果。

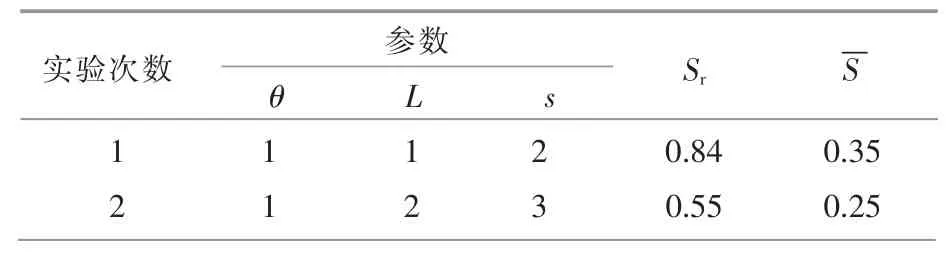
表1 正交試驗設計及結果Table 1 Orthogonal table and simulation results

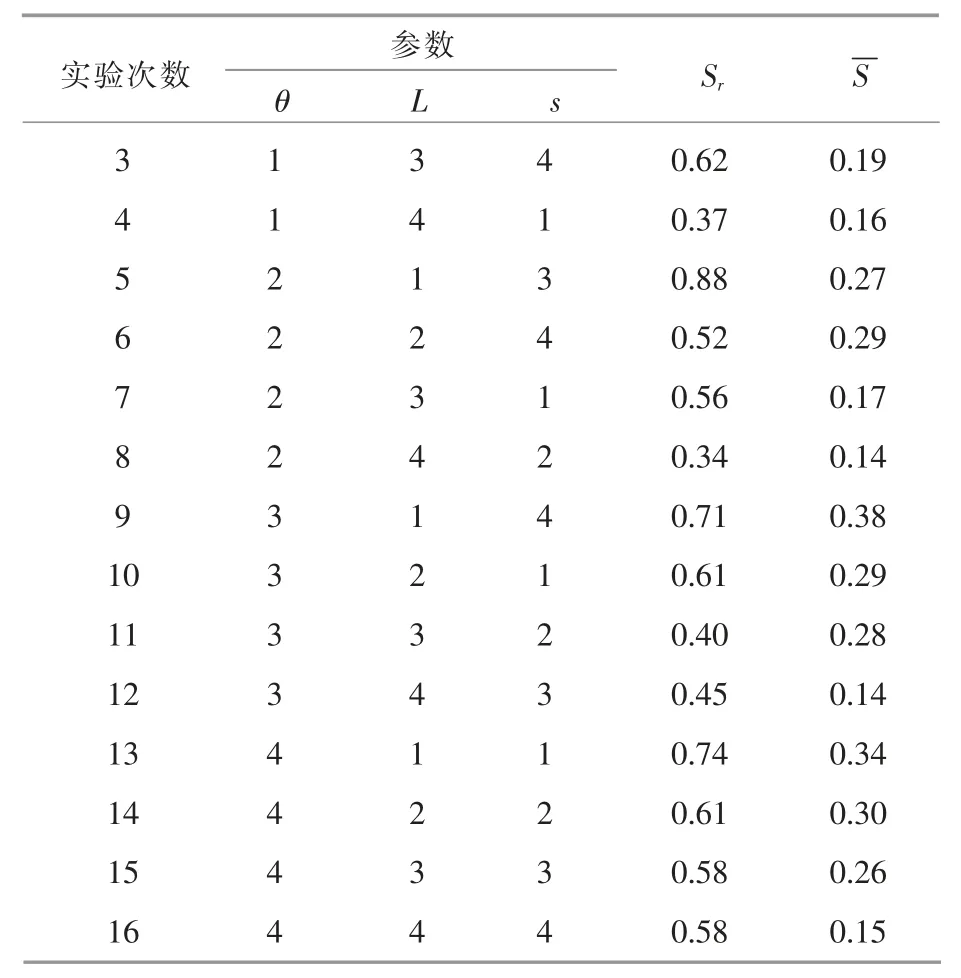
續(xù)表1

2 試驗裝置

2.1 木片樣本的制備

本研究分別選擇粒徑為0.5 cm 和1.5～2.5 cm 的蘋果樹木片（徐州德英農產品公司）作為研究對象。 首先進行樣本的制備，樣本的初始含水量為12%，預期制備含水量分別約為12%，20%，28%，35%，42%和 48%的 6 組樣本。 將每個粒徑下的木片分成6 組，分別放在塑料瓶中，根據(jù)計算好的水量在每組樣本中用小噴壺均勻噴入適量的水，靜置并定期旋轉塑料瓶，確保樣本中的水分分布較為均勻。 靜置一周之后，在每組樣本中分別隨機取3 組子樣本， 并用Mettler Toledo HE83 型標準水分測定儀測定其含水量， 取3 組測定結果的平均值作為該組樣本的標準含水量。最終得到粒徑為0.5 cm 的樣本的含水量分別為13.46% ，22.05% ，27.82% ，35.95% ，41.02% 和48.54%，粒徑為1.5～2.5 cm 的樣本的含水量分別為 12.95%，19.11%，28.86%，36.43%，43.18%和48.23%。

2.2 測量系統(tǒng)

本文搭建的測量系統(tǒng)如圖2 所示。 在試驗過程中， 將一定含水量的樣本放入電容器中，輕輕搖動，保證傳感器兩極板間的空間填滿樣本， 用 Keysight E4980AL 型 LCR 表掃頻記錄螺旋式電容傳感器在不同頻率下的電學參數(shù)。

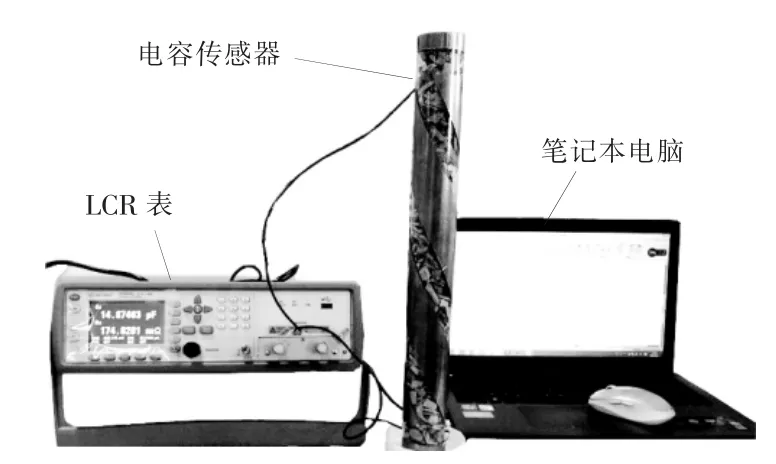
圖2 測量系統(tǒng)Fig.2 The measurement system

3 結果與討論

3.1 頻率特性分析

對兩種粒徑的樣本分別施加頻率為2×104～2×106Hz 的激勵信號， 測得不同含水量樣本的電容隨頻率的變化情況如圖3 所示。

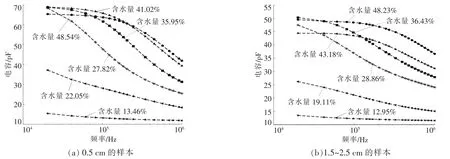
圖3 不同粒徑和含水量樣本的電容隨頻率的變化情況Fig.3 Capacitance values of samples with different particle sizes and moisture content under different frequencies

從圖3 可以看出， 不同含水量樣本的電容均會隨著頻率的增大而減小， 且兩種粒徑樣本的變化趨勢基本一致。 當激勵信號的頻率為1×105～3×105Hz 時，樣本電容隨著頻率的增加而下降的趨勢較為明顯。 當激勵信號的頻率接近于106Hz 時，樣本電容的變化趨于平緩，并漸漸趨近于一個固定值。同時發(fā)現(xiàn)，在同一頻率下，樣本的介電常數(shù)會隨著樣本含水量的增大而增大，對應的電容也相應增大。 這是因為完全干燥的樣本可以等效為絕緣體，而水作為一種極性物質，具有較大的介電常數(shù)，當樣本的含水量較高時，介質等效的介電常數(shù)也會隨之增大， 從而引起樣本電容的增大。 此外，通過對比圖3（a），（b）可以發(fā)現(xiàn)，當樣本的含水量相近時，粒徑為0.5 cm 的樣本的電容大于粒徑為1.5～2.5 cm 的樣本對應的電容。這是因為相比于小粒徑的樣本，粒徑較大的樣本的堆積密度較小， 即空隙率較大，因此，等效的介電常數(shù)較小，對應的電容也較小。

3.2 樣本含水量與電學參數(shù)之間的模型

從圖3 還可以看出，在低頻段，樣本電容容易受到外界電磁的干擾， 傳感器極板引線分布電容也會造成所得樣本電容的波動。 隨著激勵信號頻率的增大，樣本電容趨于穩(wěn)定，因此，選擇在106Hz 的頻率下建立樣本含水量與電容之間的對應模型。

兩種粒徑樣本的含水量與電容之間的關系如圖4 所示。 從圖4 可以看出，不同粒徑樣本的含水量與電容的變化趨勢基本保持一致。 通過觀察樣本含水量與電容的對應關系， 分別采用一階線性模型和對數(shù)模型對其進行擬合， 擬合結果如圖4所示。

圖4 不同粒徑樣本的含水量與電容之間的擬合曲線Fig.4 Fitting curves between water content and capacitance of samples with different particle sizes

在實際應用過程中，單一參數(shù)擬合模型的精度和可靠性達不到要求。Mizukami Y 在研究茶葉的電學參數(shù)與含水量之間的關系時，通過引入阻抗參數(shù)（Z），建立了一個同時利用 Z 和C 的多參數(shù)模型來預測茶葉的含水量，該模型的預測精度很高。

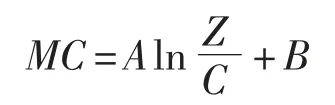
式中：A，B 均為常數(shù)。

本文利用上述多參數(shù)模型對106Hz 頻率下兩種粒徑樣本的阻抗參數(shù)、電容和含水量進行擬合，得到如圖5 所示的曲線。

3 種模型的擬合結果如表2 所示。 表2 中：SSE 為和方差，SSE 越接近于0， 說明模型的擬合效果越好；R2為確定系數(shù)， 表征擬合的近似程度，R2的值越接近于1，說明方程的擬合效果越好。

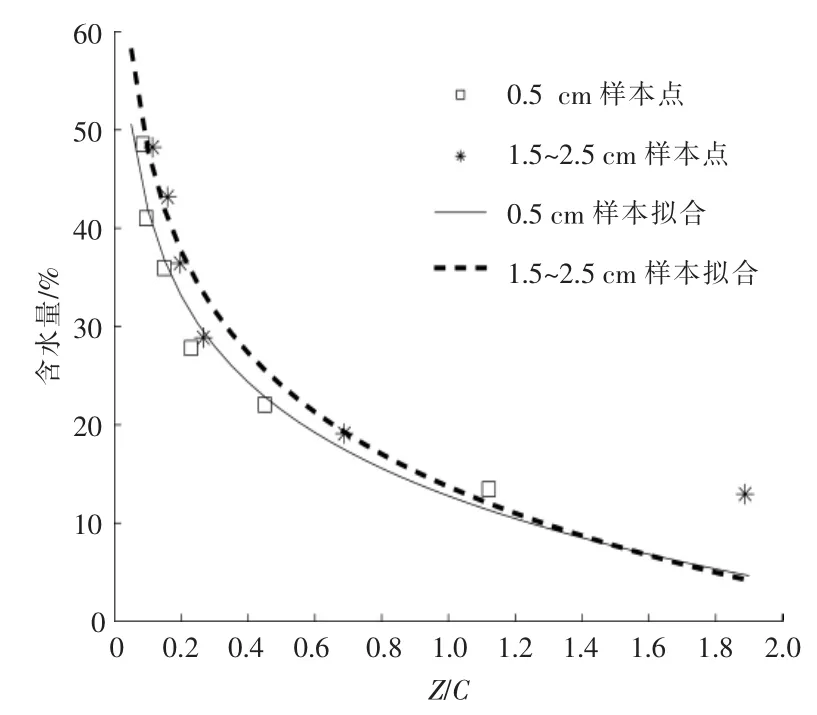
圖5 MC=Aln（Z/C）+B 模型的擬合曲線Fig.5 Fitting results of MC=Aln（Z/C）+B

從圖4，5 和表2 中可以發(fā)現(xiàn)：雖然兩種粒徑樣本的含水量與電容的關系曲線的變化趨勢相近，但是，由于不同粒徑樣本的空隙率不同，所以不同粒徑樣本的模型參數(shù)仍有差異；不同粒徑樣本的多參數(shù)模型的參數(shù)變化較小，即多參數(shù)模型對樣本粒徑的變化不敏感。通過對比3 種模型的SSE 和R2發(fā)現(xiàn)，相比于對數(shù)模型和多參數(shù)模型，一階線性模型的SSE 較小，擬合精度較高。

表2 擬合結果Table 2 Fitting results

3.3 模型驗證

為了進一步驗證擬合模型的預測結果， 制備了含水量分別為26.88%，37.73%和44.20%的粒徑為0.5 cm 的樣本和含水量分別為32.38%，34.34%和41.64%的粒徑為1.5～2.5 cm 的樣本進行驗證試驗，結果如表3 所示。 表3 中：實際值為通過標準水分測定儀測定的樣本含水量； 預測值為通過測量電學參數(shù)利用所得模型求得的樣本含水量； 模型1 為一階線性模型， 模型2 為對數(shù)模型，模型3 為多參數(shù)模型。

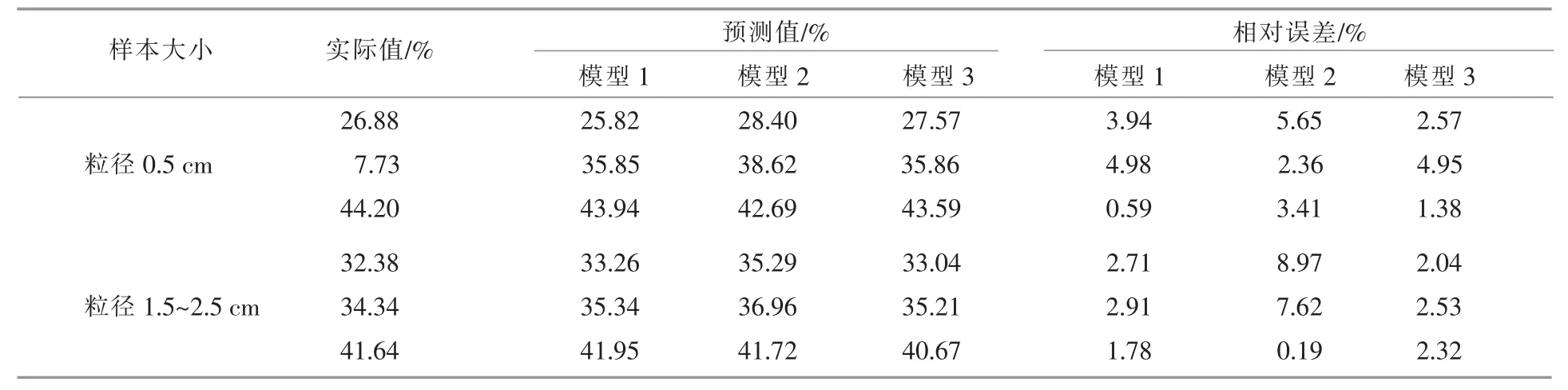
表3 模型驗證結果Table 3 Model verification result

綜合圖4 和表3 可以看出， 當樣本含水量為12%～48%時，樣本電容與含水量具有一階線性關系， 一階線性模型和多參數(shù)模型預測得到的樣本含水量的最大相對誤差在5%以內。 由于不同粒徑的樣本在傳感器中的堆積情況不同， 導致其空隙率不同，介電常數(shù)分布存在差異，從而影響所測電容的大小，導致對應的預測精度存在差異。

4 結論

生物質的含水量會影響其介電特性， 通過實驗發(fā)現(xiàn)木片的含水量與其對應的電容之間存在很好的線性相關性， 可以通過這兩者之間的關系來實現(xiàn)對生物質水分含量的預測， 本文所建立的一階線性模型和多參數(shù)模型預測得到的樣本含水量的最大相對誤差在5%以內。 不同粒徑對應的模型參數(shù)存在差異， 說明生物質粒徑的差異會對模型預測結果造成影響。 通過對比兩種粒徑樣本的模型可以發(fā)現(xiàn)， 多參數(shù)模型在不同粒徑下的參數(shù)很相近， 說明多參數(shù)的擬合可以補償由于粒徑不同引起的傳感器內空隙率分布差異對預測結果造成的影響。 同時，環(huán)境溫度、濕度等外界因素也會對預測結果造成影響， 在今后研究中可以嘗試建立多種電學和環(huán)境參數(shù)的統(tǒng)計或機器學習模型以實現(xiàn)更為準確的生物質含水量測量。