基于虛擬阻尼前饋的VSG儲能系統功率調頻解耦控制策略

趙 芳， 杜立群

（1.內蒙古建筑職業技術學院， 內蒙古 呼和浩特 010070； 2.內蒙古農業大學 機電工程學院， 內蒙古呼和浩特 010018）

0 引言

光伏、 風電等可再生能源的輸出功率具有間歇性且難以預測[1]，其大規模應用給電力系統的可靠運行及優化調度帶來了巨大的挑戰[2]，[3]。

為應對上述問題，風電、光伏配備電池儲能系統或區域電網內配置調峰、 調頻用儲能裝置逐漸成為研究熱點。 電池儲能系統作為一種柔性負荷可根據需求實現功率的吞吐。 文獻[4]介紹了一種風電場中儲能介質類型的選擇方法及容量配置策略。 文獻[5]研究了超級電容與電池混合的儲能系統在平滑風電出力中的作用。 文獻[6]進一步給出了微電網不確定運行下多種介質儲能的優化分配原則，提高了儲能系統的功率、容量等級。 文獻[7]對混合儲能系統的配置問題開展了研究， 給出了一種基于混合先進算法的配置策略。 文獻[8]研究了級聯多電平拓撲結構在大規模儲能系統中應用的可能， 并給出了一種模塊間電池均衡的調制方法。 雖然儲能系統在調節可再生能源穩定運行方面起到了積極作用， 但現有實際應用的并網儲能系統多以PQ 源形式運行， 孤島運行時多采用Vf控制或下垂控制。該傳統控制方法由于缺乏慣性，加劇了可再生能源占主導地位的微電網對擾動及故障的抵抗能力，降低了系統運行的可靠性。文獻[8]建立了儲能系統VSG 控制的寬頻帶小信號模型，為VSG 虛擬參數的整定提供了參考依據。 文獻[9]研究了光儲柴一體系統中的虛擬同步發電機控制方法。 文獻[10]對雙饋異步風力發電機的虛擬同步發電機控制穩定性進行了分析， 討論了不同場景下虛擬慣性時間常數和虛擬阻尼對小干擾穩定的影響。文獻[11]對VSG 控制變流器在LC濾波器情況下發生振蕩的機理進行了分析并給出了一種抑制方法。 上述文獻均建立在同步發電機二階暫態模型的基礎上， 對電網頻率存在偏差情況下，VSG 的一次調頻特性與阻尼環路存在的有功功率耦合問題并未闡明。 文獻[12]通過對有功的指令調節誤差積分來消除穩態誤差， 并未對一次調頻和阻尼回路的耦合問題進行討論。 文獻[13]，[14]通過在阻尼反饋回路疊加高通濾波環節，實現了穩態情況下調頻與阻尼的解耦，但該方法引入過多參數變量，加劇了VSG 有功環路穩定性分析的難度。

本文提出了一種虛擬阻尼前饋的改進型VSG 控制方法，與傳統方案對比，該方法未引入額外變量，且在電網頻率存在穩態偏差時，實現了VSG 一次調頻特性與阻尼功率環節的解耦，保證了儲能系統一次調頻的準確性。 最后，在Matlab/Simulink 中搭建的仿真模型， 驗證了本文所提策略的可行性及參數分析的有效性。

1 傳統VSG控制儲能系統的數學模型

本文儲能系統控制采用同步發電機的二階經典模型[13]，[14]。 VSG 控制儲能系統的整體框圖如圖1 所示。

圖1 VSG 控制儲能系統整體框圖Fig.1 Overview of VSG based energy storage system

圖中：Uin為儲能電池電壓；Cdc為直流側濾波電容；Lf，Lg分別為 LC 濾波器電感、 并網線路電感；R 為并網線路上寄生電阻；Cf為LC 濾波器的濾波電容。

參考同步發電機的轉子運動方程，得出VSG有功控制表達式為

式中：θ，ω 分別為 VSG 虛擬轉子的功角、角速度；ωn為額定角速度；Pr，Pe和 Pd分別為 VSG 控制中的給定功率參考、虛擬電磁功率和虛擬阻尼功率；H 為VSG 轉子的虛擬慣性時間常數。

為實現儲能系統的一次頻率調節功能， 本文采用P-f 下垂環節進行模擬，其表達式為

式中：ΔP 為一次調頻有功增量；Df為一次調頻下垂系數。

根據式（1），（2），可得本文儲能系統 VSG 控制的有功控制框圖，如圖2 所示。

圖2 VSG 有功功率控制框圖Fig.2 VSG active power of the control diagram

對于模擬同步發電機的一次電壓調節特性,本文采用Q-U 下垂控制。 無功控制環路表達式：

式中：E0為穩態虛擬電勢；Qr和 Qe分別為 VSG 無功參考及輸出無功功率；Ur為儲能系統輸出電壓幅值參考；Du為一次電壓調節下垂系數；ki為虛擬勵磁系數。

VSG 無功功率控制框圖如圖3 所示。

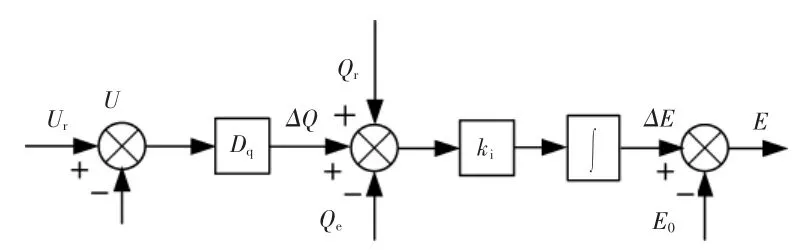
圖3 VSG 無功功率控制框圖Fig.3 VSG reactive power of the control diagram

2 VSG一次調頻與阻尼環路耦合機理分析

根據VSG 有功功率控制結構，得出傳統VSG有功閉環控制框圖，如圖4 所示。

圖4 傳統VSG 有功回路控制框圖Fig.4 Closed-loop control block of active power control

圖中SE為VSG 最大輸出有功功率， 其表達式為

式中：X 為儲能系統至電網的線路阻抗，本文忽略了線路寄生電阻對電網的影響；θ0為額定功率輸出時的虛擬功角。

根據圖4， 可推導出擾動時儲能系統輸出有功功率增量的頻域表達式為

式中：G1（s）和 G2（s）分別為 VSG 功率指令波動和頻率擾動至輸出有功功率的閉環傳遞函數。

由式（5）可以看出，輸出功率受VSG 功率指令及電網頻率波動的影響。 穩態時輸出功率增量表達式為

傳統VSG 中，不同阻尼系數對一次調頻的影響，如圖5 所示。

圖5 傳統VSG 有功環路閉環傳遞函數階躍響應Fig.5 Step response of traditional close-loop transfer function of VSG

由式（6）和圖5 可知，當電網頻率存在偏差,且在穩態的情況下，VSG 輸出有功功率的一次調頻特性與虛擬阻尼環節存在耦合關系，即VSG 虛擬阻尼特性影響了一次頻率調節的精準度。 當系統中存在多機并聯運行時， 該問題會嚴重導致各儲能單元輸出功率的不匹配。 針對此問題， 文獻[13]提出了暫態阻尼概念，使得阻尼環節僅在擾動過程中起到增強穩定性的作用， 而不影響系統穩定情況下的頻率調節。 該方法在有功環路中引入了一個額外參數，提高了參數整定難度。

本文提出虛擬阻尼前饋的改進型VSG 控制策略，如圖6 所示。

圖6 改進VSG 有功閉環控制框圖Fig.6 Improved VSG active power control loop based on feedforward damping term

由圖6 得到本文所提虛擬阻尼環路前饋后系統的閉環傳遞函數表達式為

根據終值定理可知， 穩態情況下儲能系統輸出功率增量表達式為

由式（8）可以看出，有功增量為參考指令增量與一次頻率調節功率增量之和。對比式（6）可以看出，此時VSG 有功環路中的一次調頻特性與阻尼特性實現了功率解耦，VSG 達到了一次調頻無穩態誤差功率輸出。

同樣，根據式（8），得出改進后VSG 有功環路控制閉環傳遞函數的階躍響應，如圖7 所示。除前饋阻尼系數，其余參數與圖5 保持一致。

圖7 不同前饋系數下改進VSG 有功環路閉環傳遞函數階躍響應Fig.7 Step response of traditional close-loop transfer function of improved VSG

對比圖5，7 可以看出，不同前饋阻尼系數下，當頻率受到擾動情況時， 儲能系統輸出功率始終與整定的一次調頻特性保持一致。 驗證了本文所提出的一次調頻與阻尼環節功率解耦的正確性。

3 改進VSG控制的穩定性分析

本文將對前饋阻尼控制下VSG 的穩定性進行分析，并與傳統VSG 控制方法進行對比。 根據式（7），得出改進后VSG 的自然振蕩頻率及環路阻尼系數分別為

本文中改進后的VSG 的自然振蕩頻率未發生變化，且阻尼特性仍取決于前饋阻尼系數kd，即可通過調整前饋系數的值，使得VSG 表現出不同的阻尼特性。 圖8 給出了本文所提策略中不同前饋系數時有功環路的Bode 圖，圖9 給出了不同虛擬慣性時間常數和前饋系數下VSG 控制的根軌跡曲線。

圖8 改進后VSG 有功環路頻率響應圖Fig.8 Frequency response of Improved VSG control

圖9 改進后VSG 有功環路根軌跡曲線Fig.9 Root loci of improved VSG control

由圖8 可以看出，改進后的VSG 控制在不同的前饋阻尼系數時，穩態情況下均具有單位增益，即前饋阻尼系數的引入不影響有功環路對給定功率參考的跟蹤。 再結合圖9 所示的根軌跡曲線可以看出， 在一定范圍內， 隨著前饋阻尼系數的增加，系統的阻尼特性逐漸增強。 因此，本文所提前饋阻尼策略具有與傳統阻尼方法相同的表現，且不影響系統的一次頻率調節，改進后的VSG 控制的具體參數可根據圖8，9 進行整定。

4 仿真驗證

為驗證本文所提出的前饋阻尼VSG 控制策略以及參數分析的有效性， 利用Matlab/Simulink搭建了380 V/20 kW 的VSG 控制儲能系統的仿真模型，其主要電路參數及控制參數見表1。

表1 VSG 控制儲能變流器主要參數Table 1 Main parameters of VSG based converter

利用搭建的仿真模型對傳統VSG 控制中的一次頻率調節與阻尼環節的耦合特性進行驗證。仿真開始時刻， 儲能系統輸出有功功率為0，1 s時，電網頻率突變為50.05，49.95 Hz，仿真結果如圖10 所示。

圖10 電網頻率波動±0.05 Hz 時，不同阻尼系數下仿真結果Fig.10 Simulation results under different D，with±0.05 Hz step

由圖10 可知， 當電網頻率發生變化， 傳統VSG 控制中一次調頻策略的有功增量受到阻尼環節嚴重干擾， 且阻尼系數越大， 干擾程度越嚴重。 本文提出了通過改變阻尼回路的反饋路徑實現兩者解耦的改進型VSG 控制策略。

當電網頻率波動±0.1 Hz 時， 傳統VSG 控制輸出功率波動的仿真結果如圖11 所示。

圖11 不同阻尼系數下仿真結果Fig.11 Simulation results under different D

由圖可以看出， 仿真結果與頻率波動±0.05 Hz 時相似。 均表明傳統VSG 控制下，阻尼系數對一次調頻存在干擾。

根據圖6 改進儲能系統VSG 的有功控制環路，設定初始輸出功率為0，在1 s 時刻電網頻率突降0.05 Hz，仿真結果如圖12 所示。

圖12 前饋阻尼回路控制下仿真結果Fig.12 Simulation results under different kd

由圖12 可以看出： 不同的前饋阻尼系數對VSG 暫態過程產生不同的影響，且前饋阻尼系數越大，系統超調越小，穩定性越強；電網頻率突變后，穩態時儲能系統輸出功率保持一致，即不同的阻尼系數對一次調頻功率增量不產生影響。 電網頻率波動±0.1 Hz 仿真，結果如圖13 所示。

圖13 前饋阻尼回路控制下仿真結果Fig.13 Simulation results under different kd

由圖13 可以看出，此時有功功率變化趨勢與圖12 所示仿真結果保持一致。對比改進前后的仿真結果可以看出， 本文所提出的虛擬阻尼前饋VSG 控制具有可行性。

在前饋虛擬阻尼kd=0.1 作用下，進行VSG 系統的滿功率階躍響應仿真，其結果如圖14 所示。

圖14 改進VSG 控制下儲能系統功率階躍仿真結果Fig.14 Active power step response of ESS with the improved VSG control

由仿真結果可以看出，有功功率變化平緩，不存在超調，動態響應特性較好，證明了所提方法的有效性。

5 結論

針對傳統虛擬同步發電機控制中阻尼環路與一次調頻特性存在功率耦合的問題， 本文提出了一種虛擬阻尼前饋的改進型VSG 控制方法。通過建立的頻率數學模型分析可知， 本文所提出的阻尼控制策略可實現儲能系統準確的一次調頻功率輸出，且VSG 控制的阻尼特性未發生改變。最后，在Matalb/Simulink 中搭建了380 V/20 kW 的儲能并網仿真模型， 通過對不同電網頻率突變情況下儲能系統輸出功率波形的對比仿真， 驗證了本文所提解耦控制策略的可行性以及參數分析的有效性。