基于隨機過程相關(guān)性的風電機組強度退化建模
(1.蘭州理工大學機電工程學院,甘肅 蘭州 730050;2.蘭州理工大學藝術(shù)設(shè)計學院,甘肅 蘭州 730050)
0 引言
在工程中,機械系統(tǒng)的退化過程受到多種外載荷的影響,例如:載荷、振動、溫度及其相互間的耦合關(guān)系,造成機械系統(tǒng)強度退化過程不能精確描述。隨著對航空航天材料物理性能的研究,對具有時間序列不確定量的深入探索,引入疲勞強度分析理論和隨機過程分析思想,發(fā)現(xiàn)不確定量能以某一個標準的概率分布模型進行描述,采用平穩(wěn)增長的相關(guān)性隨機過程對機械系統(tǒng)強度退化過程進行分析。應用隨機過程理論描述機械系統(tǒng)動態(tài)特性和剩余強度變化情況,達到分析零件載荷作用規(guī)律的目的,具有一定的工程使用價值。
1 機械系統(tǒng)相關(guān)性分析
本文中所分析的過程是不同狀態(tài)下的系統(tǒng)不同零部件剩余強度集中與分散之間概率分布相互獨立的情況,根據(jù)相關(guān)性分析,過去狀態(tài)的結(jié)果決定著當前狀態(tài)發(fā)生的過程,因此,必須考慮過去狀態(tài)對當前狀態(tài)的影響系數(shù),即相關(guān)系數(shù)。唐新安等人[1-4]通過對600 kW風電機組故障監(jiān)測結(jié)果分析,驗證了多種分析方法滿足故障監(jiān)測結(jié)果;周培毅等人[5]通過遺傳算法和BP神經(jīng)網(wǎng)絡(luò)運用于風電機組故障診斷中,提出了新的神經(jīng)網(wǎng)算法。安宗文[7]、屈衍靜等人[8]從強度退化過程入手,詳細分析了強度退化過程中期望值的變化規(guī)律。上述論文分析了風電機組運行過程,論述了其強度退化過程的特征,但是對概率分布的方差值的相關(guān)性沒有分析。因此,本文引入方差值的相關(guān)系數(shù)來描述剩余強度三維分布的疏密程度。
系統(tǒng)強度退化由各部件的強度退化決定的,由于各部件的強度初始強度和強度退化量不同,所以必然有最先失效的部件,失效部件滿足隨機過程,將隨機過程離散化進行分析,同時,兩個不同時刻的強度具有相關(guān)性。在整個壽命周期中,兩個不同載荷循環(huán)次數(shù)Ni,Ni+1時,(Ni
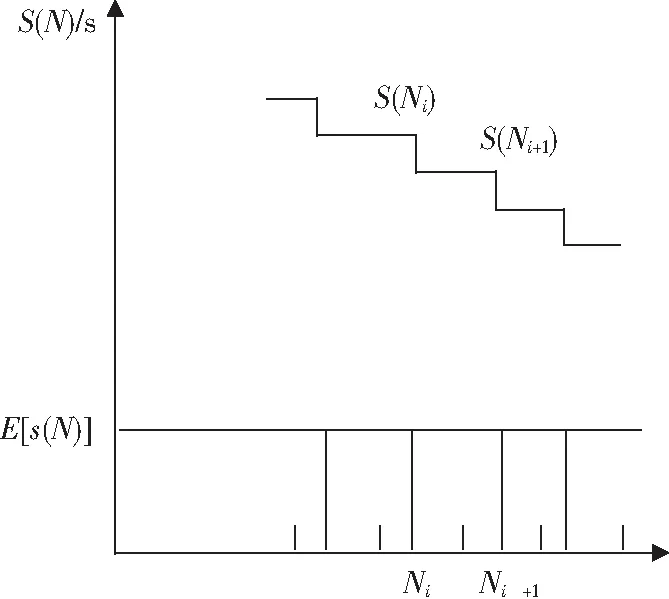
N為載荷循環(huán)次數(shù),s(N)為載荷值,S(N)為剩余強度值
根據(jù)時間序列基本理論[10],在Ni,Ni+1時刻,二維分布函數(shù)為:
F(Si,Si+1;Ni,Ni+1)=F(Si,Si+1;Ni+ε,Ni+1+ε)+
E[S(Ni)]-E[S(Ni+1)]
(1)
式中,F(xiàn)為概率分布函數(shù),S為剩余強度,Ni為載荷循環(huán)次數(shù),ε為載荷循環(huán)次數(shù)增加量。
令,ΔN=Ni+1-Ni,ΔE[S(ΔN)]=E[S(Ni)]-E[S(Ni+1)],則上式為:
F(Si,Si+1;Ni,Ni+1)=F(Si,Si+1;0,Ni+1-Ni)+ΔE[S(ΔN)]
(2)
即平穩(wěn)衰減隨機過程的二維分布疏密程度與時間起點無關(guān),只與時間間隔有關(guān)。因而其二維密度函數(shù)有:
f(Si,Si+1;Ni,Ni+1)=f(Si,Si+1;Ni+1-Ni)
(3)
2 系統(tǒng)剩余強度模型
受到載荷多次作用下,基于方差值相關(guān)性強度退化概率模型,能夠計算系統(tǒng)零部件的剩余強度分布,建立不同載荷次數(shù)下系統(tǒng)狀態(tài)之間的關(guān)系模型。在相關(guān)系數(shù)不為零的情況下,系統(tǒng)剩余強度滿足正態(tài)分布概率密度函數(shù)關(guān)系式為:
f(S,N)=f{S,E[S(N)],D[S(Ni+1)+S(Ni)]}
(4)
式中,f(S,N)為概率密度函數(shù),S為剩余強度,S0為初始強度,N為廣義外載荷作用次數(shù),E為期望值,D為方差。
系統(tǒng)零件相互作用下,系統(tǒng)剩余強度S(N)的相關(guān)系數(shù)模型:
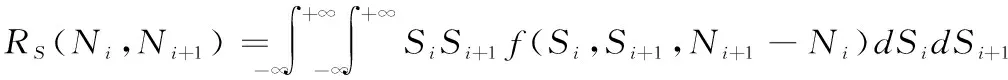
(5)
剩余強度概率模型為:
(6)
式中,h(s)為外載荷的概率分布函數(shù),R(S,N)為系統(tǒng)可靠度。強度隨機過程的方差差值:
Rs=σD(Ni)=D(Ni+1)/D(Ni)
(7)
載荷循環(huán)次數(shù)為Ni+1時,剩余強度概率分布特征的方差為:
D[S(Ni+1)]=D[S(Ni)]×Rs
(8)
3 風電機組系統(tǒng)剩余強度建模及分析
風電機組所承受隨機載荷是基于期望值上下波動的分布特性,滿足平穩(wěn)隨機過程特性,具有右連續(xù)性、相關(guān)性。本文中研究對象為增速齒輪箱輸出軸,屬于外齒輪軸,由于其傳遞扭矩大,轉(zhuǎn)速高,因此,選擇材料為17CrNiMo6的高強度滲碳合金鋼作為增速齒輪箱輸出軸,初始強度為1 360 MPa,初始方差為2.7 MPa2,滿足正態(tài)分布,材料力學性能符合GB/T3077-1999,JB/T6396-1992,JB/T6396-2006要求。假設(shè)剩余強度按照線性退化,在不同載荷作用次數(shù)下,剩余強度期望值如表1所示。
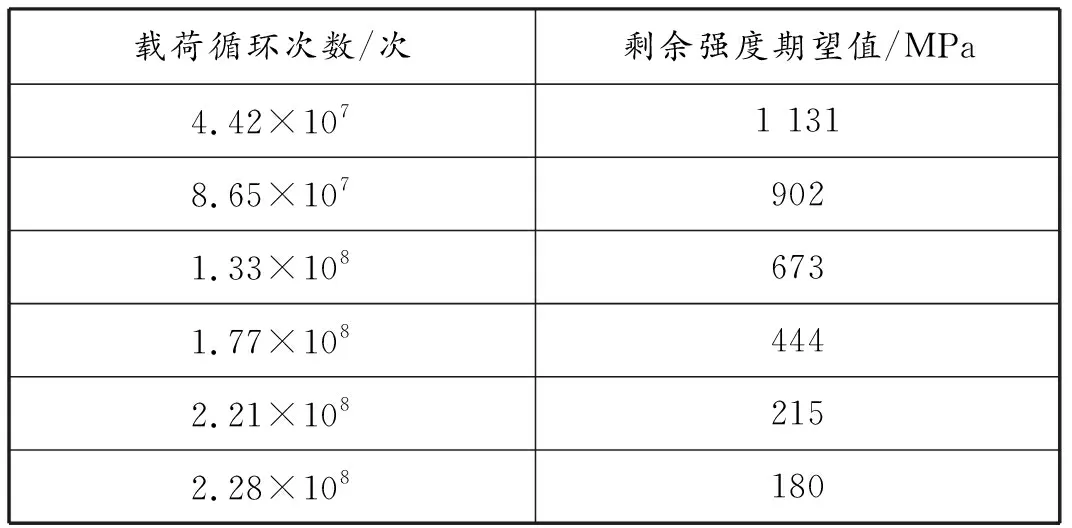
表1 輸出軸剩余強度值
則剩余強度的概率分布為:
f(S,N)=f{S,E[S(N)],D[1 360+S(N)]}
(9)
載荷作用次數(shù)為Ni與Ni+1時刻測試點方差分布(見表2、表3)。
運用MATLAB曲線擬合模塊獲得方差相關(guān)系數(shù)模型如圖2所示。

表2 測試點方差分布

表3 方差差值分布
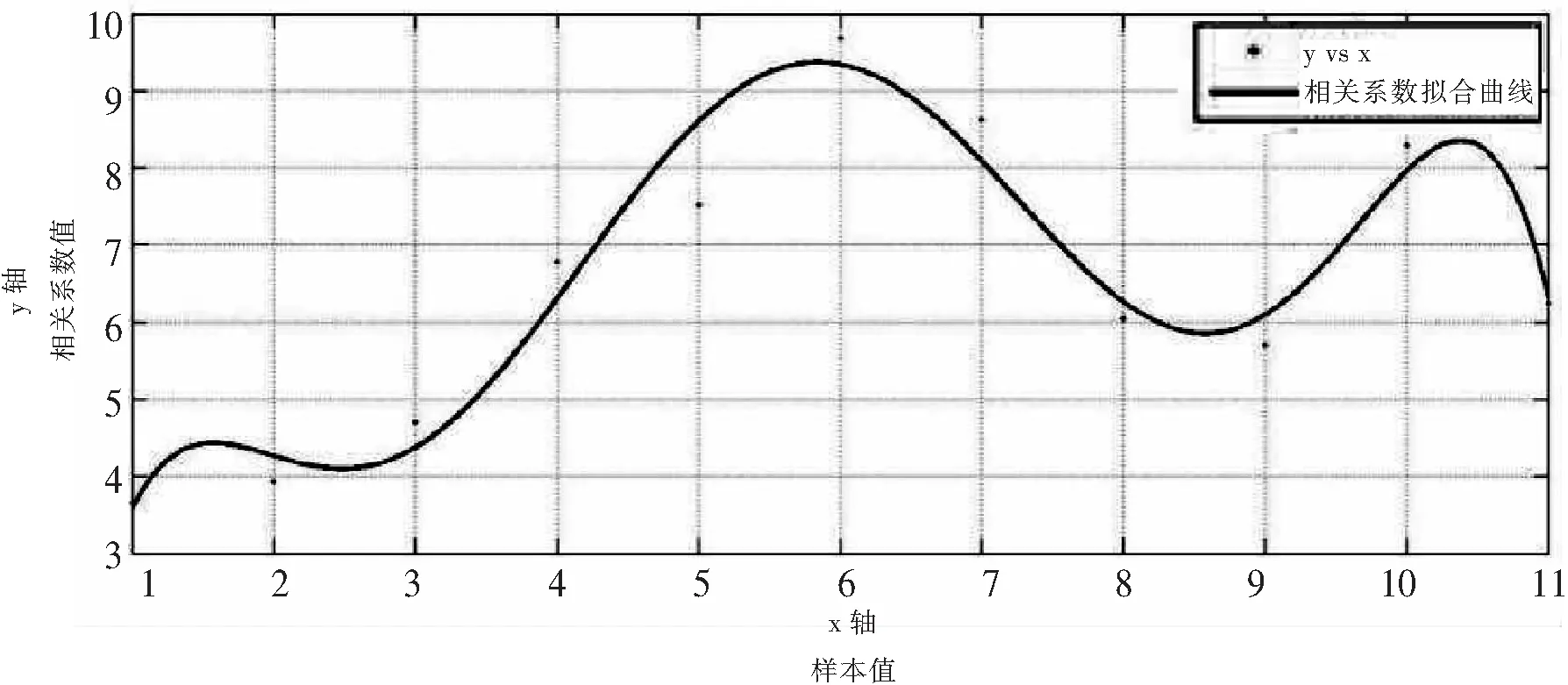
圖2 相關(guān)系數(shù)擬合曲線
相關(guān)系數(shù)擬合模型如下式所示:
Rs[D(Ni+1)]=-0.002 871×D(Ni)5
+0.095 87×D(Ni)4-1.171×D(Ni)3
+6.198×D(Ni)2-12.5×D(Ni)+11.31
(10)
運用MATLAB隨機曲線模塊與三維圖像模塊仿真分析:
剩余強度概率分布期望值大于應力值時,其概率分布與與應力值相距很遠。載荷循環(huán)次數(shù)差值縮短時,可以看出剩余強度的三維概率分布滿足峰值逐漸降低,分布面逐漸出現(xiàn)發(fā)散現(xiàn)象。
剩余強度概率分布三維曲面的峰值逐漸接近應力分布的峰值,其概率分布也逐漸發(fā)散,證明機械系統(tǒng)整機故障率在升高。剩余強度趨近于應力值時,其概率分布只有也逐漸趨于0值,只有12條直線分布,證明大部分風電機組已經(jīng)失效,只有概率值的一部分機組能夠運行,其可靠性也趨于零。因此,當接近某一個載荷作用次數(shù)時,期望值趨于零,方差值趨于無窮大。
4 結(jié)論
根據(jù)時間序列分析方法,采用隨機過程相關(guān)性的理論推導分析表明,系統(tǒng)部件動態(tài)相關(guān)性與時間間隔有關(guān),根據(jù)MATLAB仿真結(jié)果可以看出,在風電機組中,隨著載荷循環(huán)次數(shù)的增加,零部件剩余強度的概率分布逐漸趨于零平面,強度隨機值與期望值的偏離值趨于發(fā)散,發(fā)散速度與強度退化速率相關(guān),同時,通過應力強度分析表明,正常工作風電機組數(shù)量也在減少。建立動態(tài)方差變化與系統(tǒng)強度退化之間的仿真模型,能夠有效地描述機械系統(tǒng)的作用規(guī)律,為提高機械的可靠性能提供了理論依據(jù)。

