全息凹面光柵光譜儀信號復(fù)原技術(shù)研究

(南京郵電大學(xué) 自動化學(xué)院, 南京 210000)

分辨率在光譜儀器中是非常重要的一項技術(shù)指標(biāo)，它直接影響著儀器的分析能力。光譜儀的分辨率主要是由其使用的硬件所決定，如狹縫線寬，準(zhǔn)直鏡口徑，光柵刻線密度，光柵口徑等等[1]。分辨率不足會導(dǎo)致光譜信號發(fā)生混疊難以分辨，光譜信號復(fù)原技術(shù)則是一種能夠在一定程度上提高儀器分辨能力的數(shù)學(xué)方法[2]。

通常，光譜信號復(fù)原需要獲知儀器的光譜響應(yīng)函數(shù)作為一種先驗信息，為了獲取儀器的光譜響應(yīng)函數(shù)，常用的方法有直接計算法和測量法，計算法需要獲得儀器的設(shè)計參數(shù)，再利用光學(xué)衍射方程來求解光譜響應(yīng)函數(shù)的近似解，這種方法雖然可以直接通過計算得到儀器的響應(yīng)函數(shù)，但是對于大多數(shù)商用儀器來說儀器的設(shè)計參數(shù)是商業(yè)秘密通常不會公開，且由于系統(tǒng)中的各種誤差影響，計算得到的結(jié)果往往和實際值存在偏差。

相比較計算法，測量法是使用一些能產(chǎn)生窄線寬光譜的光源作為輸入光源，直接測量得到光譜沖擊響應(yīng)曲線，但直接測量得到的結(jié)果中包含有各類噪聲不能直接作為先驗信息，因此需要進行曲線擬合從中提取得到較為可靠的解。曲線的擬合都需要以某種數(shù)學(xué)模型為對象，目前市場上大部分光譜儀多采用Czerny-Turner結(jié)構(gòu)，此光譜儀的像差校正比通常較為完善，因此儀器的沖擊響應(yīng)曲線可以被高斯曲線很好的近似[3-5]。全息凹面光柵光譜儀的成像離軸角度較大，成像系統(tǒng)存在著較大的慧差[1，6，7]，實驗發(fā)現(xiàn)全息凹面光柵光譜儀的光譜響曲線向一側(cè)發(fā)生傾斜，左右并不對稱，而高斯模型則是一種典型的左右對稱模型，直接使用高斯模型提取儀器響應(yīng)函數(shù)必然是無法得到準(zhǔn)確結(jié)果的。

針對這個問題，本研究提出了一種基于全息凹面光柵光譜儀光譜響應(yīng)曲線的改進模型，利用改進模型擬合提取出的結(jié)果作為算法的先驗信息輸入，利用基于泊松隨機場的反卷積算法完成全息凹面光柵光譜儀的信號復(fù)原。

1 全息凹面光柵光譜儀點擴散函數(shù)模型

全息凹面光柵光譜儀中產(chǎn)生色散的元件是全息凹面光柵，光源發(fā)出的光線由狹縫進入儀器照射在全息凹面光柵上發(fā)生色散并聚焦，最終成像于探測器陣列上。

光譜儀的點擴散函數(shù)是狹縫衍射，光柵衍射和光學(xué)系統(tǒng)綜合像差共同作用的結(jié)果，進而可以被概括為如下的卷積表達式(1)。

hobservation=hslit*hgrating*haberration(1)

其中*為卷積運算符號。hslit為狹縫衍射卷積函數(shù)，具體形式如式(2)，ω為狹縫寬度，f2為成像焦距，λ為入射光波長，x為像面位置。

(2)

式(3)為hgrating為光柵衍射卷積函數(shù)，其中ωg為光柵刻槽寬度，d為光柵常數(shù)，N為光柵刻線數(shù)。

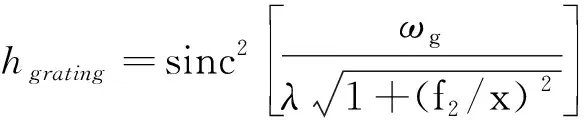
(3)

式(4)haberration為光學(xué)系統(tǒng)綜合像差卷積函數(shù)可近似為

haberration≈exp(-a(λ)x2)

(4)

在實際工程中為了簡化計算，通常將光譜儀中的hobservation函數(shù)的最終形式近似為高斯函數(shù)[8，9]。

對于全息凹面光柵光譜儀，綜合像差卷積函數(shù)需要被被分解為離焦hdefocus和慧差hcoma兩部分,雖然hdefocu通常可以被近似為一個高斯函數(shù)，但hcoma卻比較特殊，因為慧差對光強能量分布的影響類似于彗星，實際慧差所形成的光強分布的理論公式極為復(fù)雜且繁瑣非常不利于處理計算，出于方便實際數(shù)據(jù)處理和減小計算量的考慮，工程上需要尋找一種簡化的同時又能很好的反映慧差特性的函數(shù)。從Namioka T , Seya M等人發(fā)表的關(guān)于全息凹面光柵的文獻中發(fā)現(xiàn)，該類光柵譜線表現(xiàn)出的光強分布特點是在某一點處光強很強，再從該點開始向某一側(cè)光強急劇減小而另一側(cè)光強則為零[6，7]，根據(jù)這一特性同時為了簡化計算起見，本文將hcoma近似為一側(cè)區(qū)間上的指數(shù)函數(shù)，如式(5)。

hcoma≈exp(-b(λ)x)；x≥0

(5)

綜上全息凹面光柵光譜儀的點擴散函數(shù)的簡化模型可寫成式(6)

hobservation=hGaussian*hcoma

(6)

hGaussian=exp(-c(λ)x2)

(7)

hcoma=exp(-b(λ)x)；x≥0

(8)

因此最終的擬合式如式(9)

h=d(f*g)+c

(9)

(10)

(11)

其中常數(shù)項c用來描述傳感器中的底噪的期望值，d是幅值。

2 基于泊松隨機場的反卷積算法介紹

在光學(xué)成像系統(tǒng)中，圖形中的噪聲常常呈現(xiàn)出泊松分布的形式，而一個隨機變量X具有泊松分布，指的是其取整數(shù)k的概率可以被式(12)所表達

(12)

其中λ是X的期望。

因為光譜儀得到的數(shù)據(jù)是一行數(shù)組，所以可以用x和y來描述整個光譜儀輸入和輸出圖形，xn和yn表示對應(yīng)像素點的值，則光譜儀的系統(tǒng)模型可以表示為式(13)。

(13)

其中hi表示儀器點擴散函，vi表示對應(yīng)像素點的噪聲。而在無噪聲情況下的系統(tǒng)期望信號可由式(14)給出。

(14)

則在給定原圖形為x而實際觀測為y，系統(tǒng)噪聲模型為泊松模型下的概率分布式(15)

(15)

該式為泊松分布似然函數(shù)，可以利用最大似然估計原圖形x。對其兩邊取對數(shù)可得最大似然估計式(16)。

(16)

為求P的極大值，繼續(xù)求p對x的偏導(dǎo)，并令結(jié)果為0，得式(17)。

(17)

因為對點擴散函數(shù)h求和結(jié)果恒為1，故進一步有式(18)

(18)

對其使用迭代法，可得x的最終迭代式(19)[9-11]。

(19)

3 實驗結(jié)果

3.1 光譜響應(yīng)曲線擬合結(jié)果

實驗使用GP3HG-1低壓汞燈和一臺自行研制的全息凹面光柵光譜儀工程樣機進行，該汞燈可以產(chǎn)生自然展寬遠小于儀器極限分辨率的窄帶光譜[12]，以此作為儀器的激勵信號，測量全息凹面光柵光譜儀的響應(yīng)，本研究提取了汞燈譜線中分布較為獨立并且信噪比較高的幾個波長，分別進行歸一化，如圖1所示。 從圖中可以看出系統(tǒng)的實測信號中覆蓋有一層底噪其為系統(tǒng)的暗電流噪聲，暗電流噪聲是傳感器所固有的一種電噪聲其期望值為一常量，因此需要在擬合模型中加入一個常數(shù)項作為其期望值，并在擬合過后去除這個常數(shù)項。

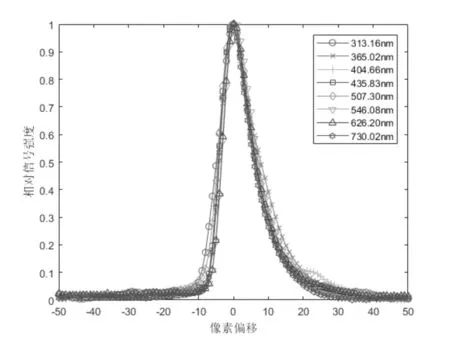
圖1 歸一化并對齊譜峰后的8個波長的響應(yīng)曲線

首先對測得的幾個波長譜線歸一化結(jié)果求取均值，再利用改進模型對其進行最小二乘擬合，再減去擬合式(11)中用來描述暗電流噪聲的常數(shù)項c，并令幅度值d等于1后就可以得到估計的儀器點擴散函數(shù)如圖2所示。圖3則為高斯模型直接擬合的結(jié)果，觀察圖2和圖3相比較圖1，從直觀上已經(jīng)能看出改進模型能更好的反映儀器的響應(yīng)特征。

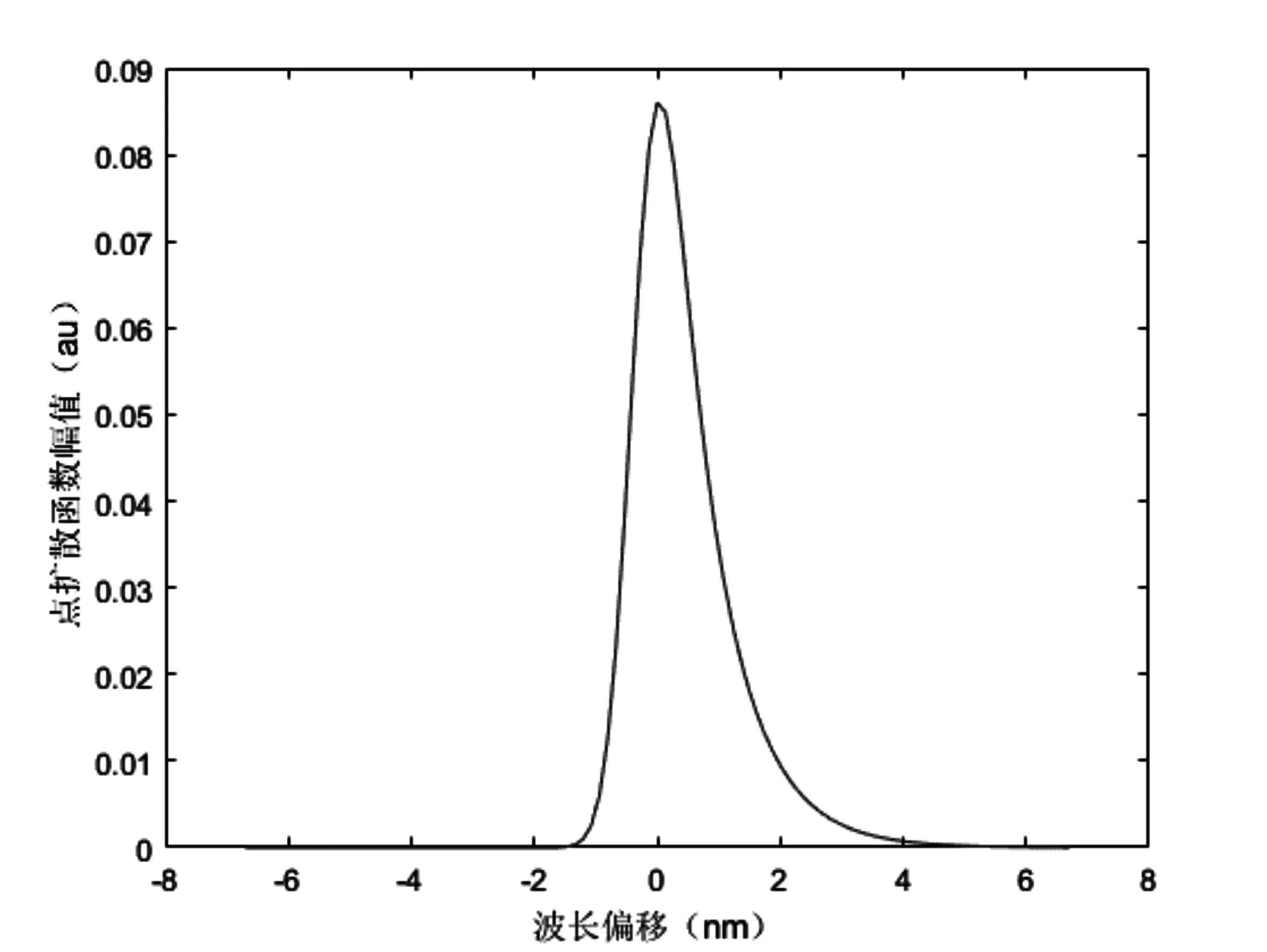
圖2 改進模型擬合的光譜儀點擴散函數(shù)

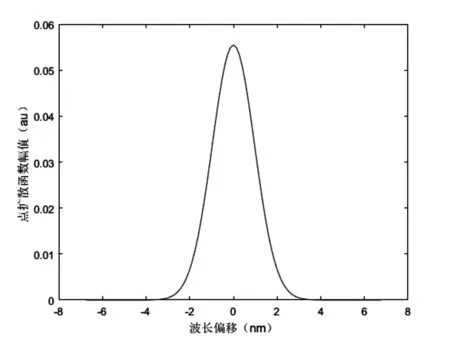
圖3 高斯模型擬合的光譜儀點擴散函數(shù)

表1給出了兩者模型的客觀擬合效果，通過表1可知改進模型對比高斯模型在殘差平方和，均方根誤差，R方系數(shù)等評價擬合效果的關(guān)鍵指標(biāo)上都有了顯著的提高。因此本研究所提出的改進模型相比較高斯模型能更好的描述全息凹面光柵光譜儀的光譜沖擊響應(yīng)曲線。

表1 兩種模型的擬合效果評價

3.2 改進模型的光譜復(fù)原結(jié)果

為了進一步地驗證改進模型對全息凹面光柵光譜儀信號復(fù)原的效果，繼續(xù)使用GP3HG-1低壓汞燈作為全息凹面光柵光譜儀的測試光源。分別用高斯模型擬合出的點擴散函數(shù)和改進模型擬合出的點擴散函數(shù)作為算法的先驗信息，算法迭代次數(shù)均設(shè)為20次[13]，并與實測信號進行對比。實測信號為實際光譜分析中較為有代表性的兩種情況，分別為對稱光譜雙峰和不對稱光譜雙峰，第一組為峰值在2065像素點和2081像素點的，576.96nm和579.07nm波長對稱光譜雙峰如圖4，第二組為峰值在2419像素點和2427像素點的，625.20nm和626.20nm波長不對稱光譜雙峰如圖5，半高全寬(FWHM)均為1.37nm，兩組信號都受到了儀器分辨能力的限制發(fā)生了一定程度的光譜重疊。

復(fù)原效果的評價主要依據(jù)為復(fù)原過后光譜的半高全寬(FWHM)和復(fù)原后光譜譜峰的對應(yīng)波長位置相比較真實值的改變量[14，15]。

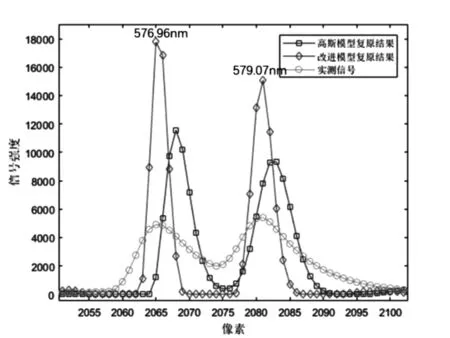
圖4 對稱光譜雙峰復(fù)原效果

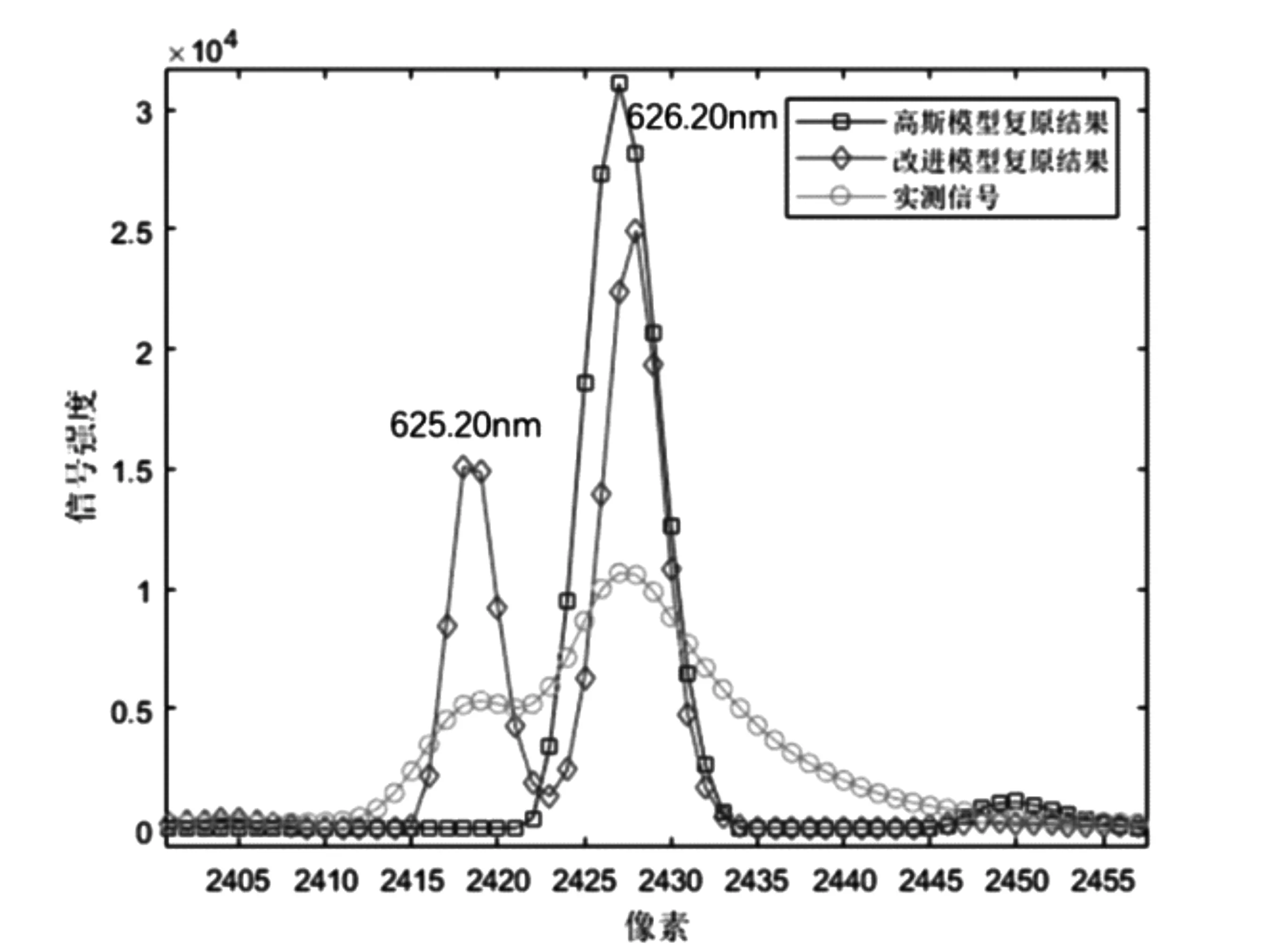
圖5 不對稱光譜雙峰復(fù)原效果

結(jié)合圖4和圖5和表2，可以明顯看出以改進模型擬合出的點擴散函數(shù)作為先驗信息的復(fù)原結(jié)果，在對稱光譜雙峰的例子中，譜線半高全寬和光譜波長定位準(zhǔn)確度上都比高斯模型有了明顯的提高。而在不對稱光譜雙峰的例子中，改進模型的半高全寬依舊要優(yōu)于高斯模型，但值得注意的是，在高斯模型下不對稱雙峰復(fù)原的結(jié)果中丟失了625.20nm的光譜曲線，這是由于高斯模型本身并不能準(zhǔn)確的描述儀器響應(yīng)所致，因所提供的先驗信息不準(zhǔn)確，進而在復(fù)原過程中出現(xiàn)了較為嚴(yán)重的錯誤，復(fù)原結(jié)果也完全失去了參考的價值。改進模型下的復(fù)原結(jié)果則不存在這種情況，復(fù)原的光譜中保留了所有光譜特征信息。 總得來說改進模型相比較傳統(tǒng)儀器中常用的高斯模型，能夠更好的反映出全息凹面光柵光譜儀的光譜響應(yīng)曲線，利用改進模型得到的儀器響應(yīng)函數(shù)做為光譜信號復(fù)原算法先驗信息輸入，更具有有效性和正確性。

表2 兩種模型對應(yīng)兩種類型光譜雙峰復(fù)原結(jié)果

/表示不存在

4 結(jié)論

針對傳統(tǒng)光譜儀中常用的高斯模型存在的不足，本文提出了一種基于全息凹面光柵光譜儀的光譜響應(yīng)曲線改進模型，利用低壓汞燈產(chǎn)生的脈沖光譜測得了一臺全息凹面光柵光譜儀的實際光譜響應(yīng)，并分別利用本文提出的改進模型和傳統(tǒng)高斯模型，提取了儀器的光譜響應(yīng)函數(shù)，并作為輸入光譜信號復(fù)原算法的先驗信息分別測試實際光譜信號復(fù)原效果，實驗結(jié)果表明在全息凹面光柵光譜儀中改進模型相對于高斯模型更加有效。