光彈性顆粒的線掃描測力方法

陳福星,楊朝宇,邵榮生,黃旋格,張興剛

(貴州大學 物理學院，貴州 貴陽 550025)

光彈性效應[1]在研究顆粒物質也具有很大的意義. 采用光彈性研究二維顆粒，可通過拍攝光彈性顆粒上的全場光強分布，從而獲取顆粒在偏振光場中的干涉條紋分布圖，即應力光圖. 應力光圖反映了二維顆粒的應力分布. 通過應力光圖反應的應力分布，可能反推出顆粒邊界上的接觸力大小. 數字圖像的處理[2-3]與二維顆粒的光彈性理論相結合，通過應力光圖獲知加載力大小及顆粒接觸點位置等信息. 光彈性理論的難點在于光彈性模型的應力分布的求解[4]. 對于兩點對心對稱加載顆粒[5-6]的理論已經有較為全面的研究. 而要處理顆粒的多點不對稱接觸的復雜情況，則需要更加完善的多點接觸圓盤理論[6-7].

杜克大學Behringer等，用光彈顆粒實驗探究了力網、力的概率分布、顆粒物質的堵塞態和堵塞轉變等問題[8-9]，包括使用對顆粒的應力光圖的等差條紋圖進行非線性最小二乘法擬合獲取顆粒的加載力大小的方法，但該方法是對每個顆粒的全場光強進行擬合，在應用中有較大的運算量，且只有當3維圓柱顆粒的接觸方式接近線接觸時才較為實用，其對實驗拍攝的應力光圖的精度要求也較高. 基于平均平方灰度梯度獲取平均接觸力[10-11]的經驗方法，在處理大量顆粒平均接觸力時較為適用，但它不能得到顆粒上各個加載點的精確的加載力大小，只能獲得顆粒接觸力的平均值. 通過對顆粒進行閾值切割從而實現幾何形態學操作的方法可以獲取顆粒圓心位置、大小、接觸點[11-12]. 然而這種方法檢測接觸點時，存在拍攝角度、圖像識別精度等問題，可能會把2個靠得很近卻不接觸的顆粒識別為相互接觸. 這樣在計算平均接觸力時，由于接觸點的數目的誤判，會帶來平均接觸力大小的判斷錯誤. 另外對于單個顆粒，或者顆粒堆邊緣處的顆粒，要通過該方法獲取接觸點位置也是不可能的.

為了解決顆粒閾值切割尋找接觸點的位置出現誤判，并能尋找邊緣處顆粒或者單個顆粒的接觸點位置，需要一種新的尋找接觸點方法. 而為了解決對顆粒的全場光強進行的非線性擬合方法運行慢、依賴線接觸方式的問題，考慮對顆粒全場光強的擬合轉換為對顆粒上幾條連線的光強進行擬合，即對顆粒的應力光圖進行線掃描.

1 二維多點加載的顆粒的光彈性原理

光彈性實驗光路如圖1所示，在正交圓偏光場中，對于半徑為R的二維光彈性材料的顆粒圓盤，存在厚度的三維圓柱，在其圓邊界處若存在點加載的載荷，由于光彈性材料的暫時雙折射效應，會出現明暗分布的等差條紋. 條紋的光強[1]為

(1)

其中，Ia為光源光強，δ為某處光彈性材料的相位，N為條紋級數，對于整數級的條紋，如N=0，1，2，…，光強I為0. 又比如當I=Ia/2時對應的條紋級數為N=1/4，3/4，5/4，…

光彈性顆粒上每個位置的相位都由其應力分布得到，即二維應力光學定理：

δ=2π(σ1-σ2)h/f,

(2)

其中(σ1-σ2)，h和f分別為主應力差、模型厚度和材料條紋值.

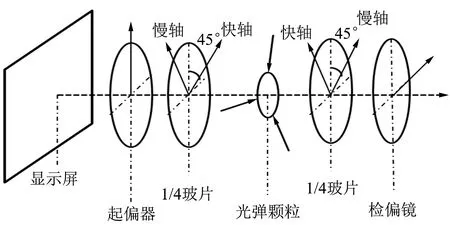
圖1 光彈性實驗光路圖

要求得光彈性顆粒光強的分布，還需要求出多點加載時顆粒圓盤各處的主應力差(σ1-σ2). 求出單點載荷在圓盤上的應力分布，通過應力的疊加原理，即可得到多點加載的圓盤的應力分布.

如圖2所示，對于過顆粒模型圓心的加載力F，要求它在圓盤上產生的應力分布，可以建立以加載點為原心的坐標系O1，以及在圓心處建立的直角坐標系O.O1坐標系y軸與O坐標系的y軸夾角為α，在圓心坐標O中，圓盤上任意一點坐標可表示為(r,θ)，r為P點到圓心距離，θ為P點到原心連線與y軸的夾角.

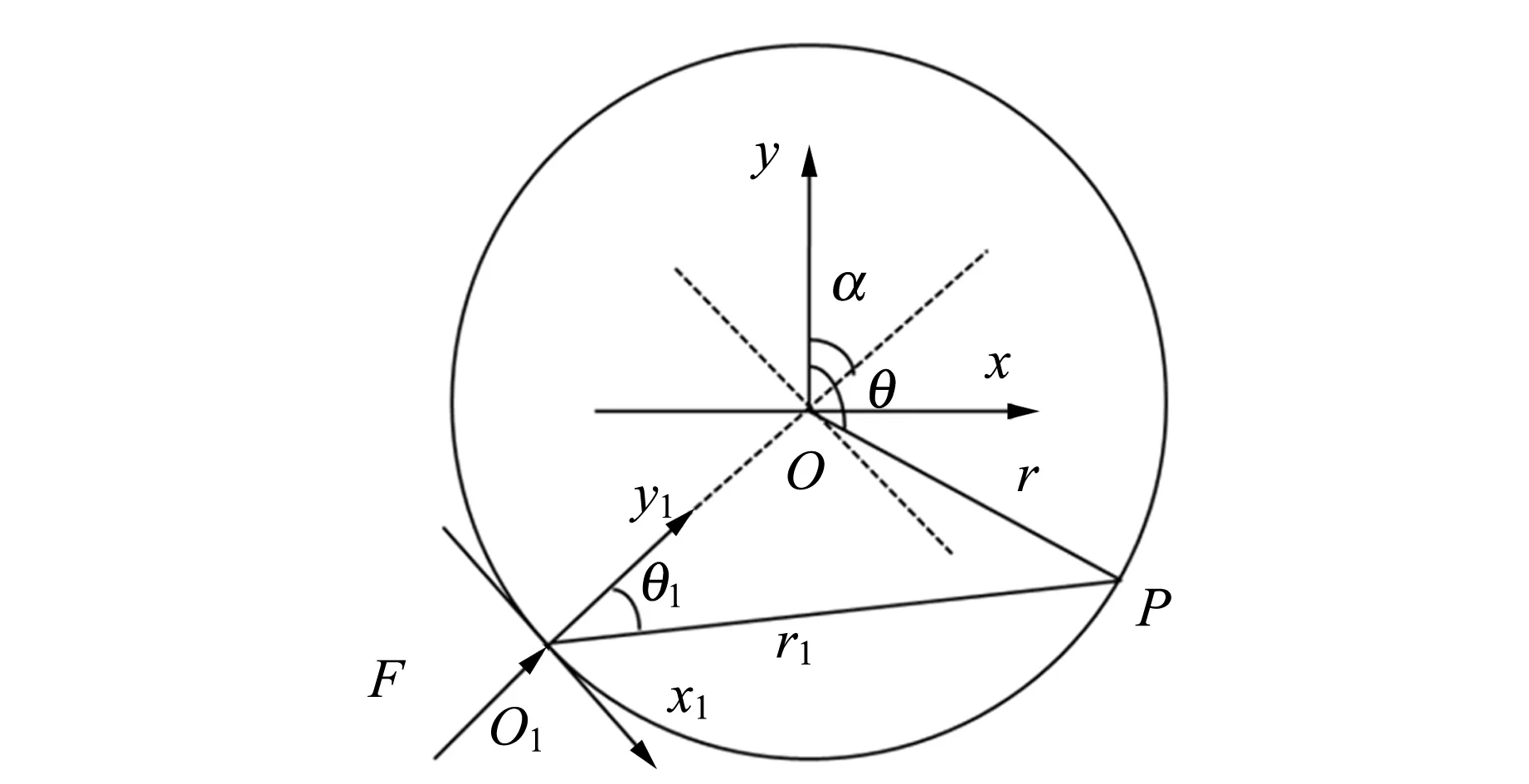
圖2 與O坐標系的y軸夾角為α的力作用在顆粒模型上的示意圖

同時，P點也可在O1坐標系下的坐標可表示為(r1,θ1)，在O1坐標系中可給出力F在y軸的正半平面中的應力函數[7]為

(3)

為了方便應力疊加，將應力函數在O坐標系中表示. 坐標系O的可由坐標系O1先通過平移R距離再逆時針旋轉α變換而來，由幾何關系

(4)

則坐標系O下的F產生的應力函數寫為

(5)

應力張量可以由應力函數[4]表達為

(6)

如圖3所示，現在考慮有i個點加載力作用在圓盤上，若考慮在顆粒圓盤邊界處的加載均為無摩擦的對心點加載，現考慮這i個點加載力半平面的應力疊加近似為圓盤上的應力分布，其表達式為

(7)

由于主應力差為

(8)

即可由此得到顆粒圓盤的光強分布. 雖然是近似結果，在模擬中發現其完全能夠滿足實驗的要求.

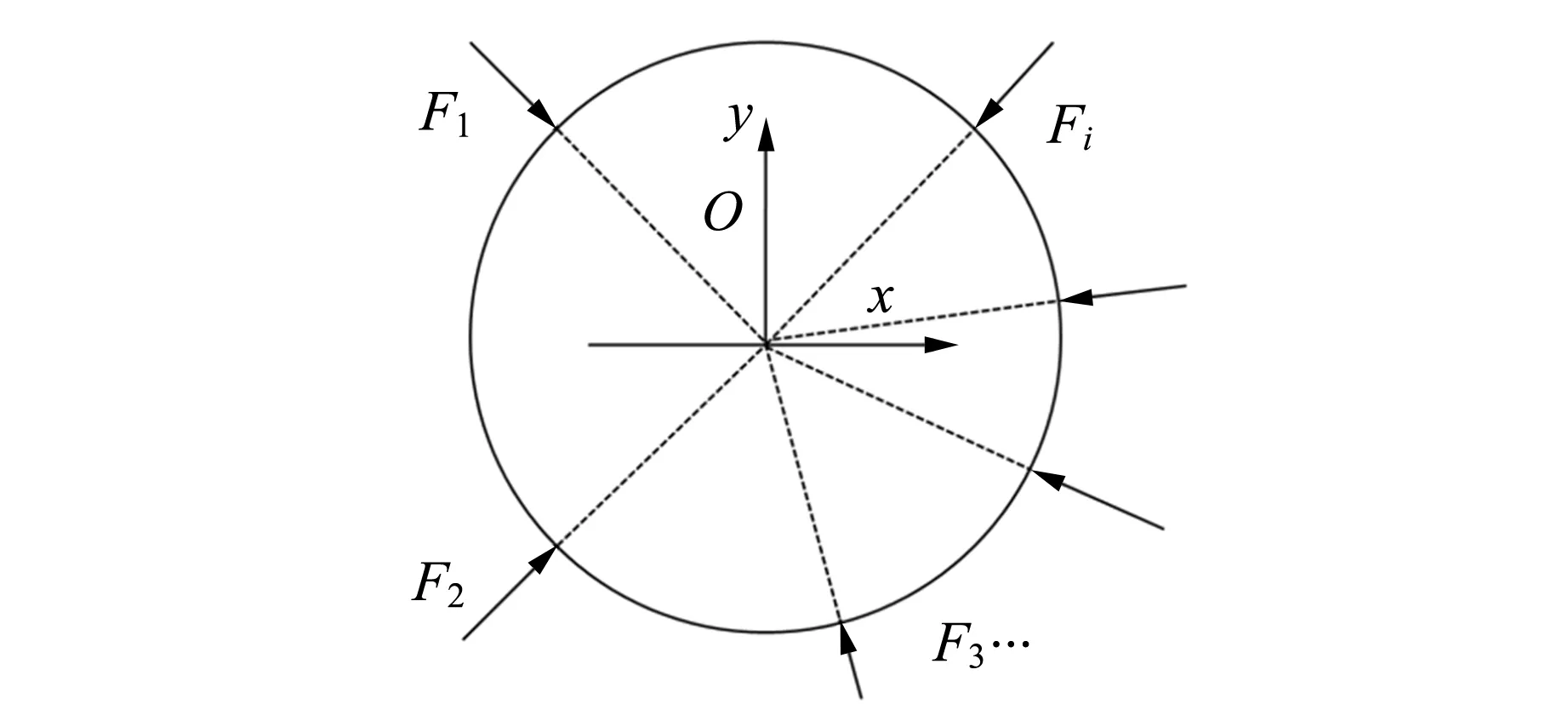
圖3 多個力(F1,F2,F3,…,Fi)作用在顆粒上的示意圖

2 加載實驗裝置

為搭建多點加載顆粒的實驗裝置如圖4所示，可先設計所需的具有不同加載點位置的加載裝置的模型，并使用3D打印機打印制作，安裝螺旋微分頭. 為了能夠實現在顆粒上進行多點加載，同時也能夠檢測出加載力的大小，需要在螺旋微分頭與顆粒圓盤之間放置力傳感器. 要使力傳感器的檢測頭能與螺旋微分頭之間不出現相對滑動，還需要使用3D打印制作小的力傳感盒來固定測微頭與應力檢測頭的相對位置. 搭建正交圓偏光場，需要打印能搭載偏振片和1/4玻片的裝置，該裝置應能實現玻片與偏振片的在一定角度范圍內的旋轉，以方便調節得到正交圓偏光場. 另外由于顯示屏上已有偏振膜，所以不用再添加起偏鏡，僅需要旋轉調節1/4玻片與檢偏鏡即可得到正交圓偏光場.

圖4 實驗裝置搭建與加載裝置示意圖

制作光彈顆粒時，可先使用3D打印機打印凹形圓柱硅膠模具的模具，由于打印精度的問題，在模具圓面會有一定程度的粗糙，可使用細砂紙將其打磨平整. 使用硅膠澆筑，得到光彈性材料的硅膠模具. 另外，為了制作能在力傳感器的檢測范圍內有豐富圖案變化的光彈性顆粒，可調試需要的比例，將環氧樹脂的軟膠和硬膠按需求進行混合，可澆筑得到不同材料條紋值的顆粒試件.

3 對顆粒應力光圖的數字圖像處理

3.1 顆粒圓盤的邊界、圓心、半徑的提取

獲得顆粒實驗的應力光圖如圖5(a)所示，可以發現，由于二維顆粒存在一定厚度，對環境光源有折反射，在顆粒邊界處，也有一定的光強. 可通過簡單的閾值二值化[圖5(b)]、閉操作以及填充操作獲得顆粒圓盤的范圍[圖5(c)].

(a)實驗顆粒應力光圖

(b)對實驗應力光圖進行閾值二值化

(c)閉操作及填充操作得到顆粒形態矩陣圖5 顆粒圓盤的邊界、圓心和半徑的提取

對顆粒圓盤范圍圖5(c)進行遍歷，可以確定顆粒圓盤范圍內的像素點，通過質心公式得到圓盤圓心. 統計模型范圍內像素點數，即可用圓面積公式得到圓盤的半徑[12]. 如此將顆粒圓盤的邊界抽象為圓.

3.2 邊界圓模板尋找加載點位置的方法

當處理多顆粒接觸問題時，可直接采用閾值分割的方法對顆粒幾何形態學操作獲取顆粒的邊界，對2個顆粒邊界相切的位置即可直接判斷為接觸點位置[11-12]. 然而這種方法檢測接觸點時，存在拍攝角度、光照、圖像識別精度等問題，會把2個靠得很近卻不接觸的顆粒識別為相互接觸. 另外有一種情況，雖然顆粒接觸但卻沒有接觸力存在，這樣把它判斷為接觸也是不合適的.

本文提出直接通過邊界圓模板尋找加載點位置的方法. 直觀觀測得知，接觸點的位置即條紋產生的位置，高級條紋在接觸點附近密集，于是其位置對應的像素灰度梯度方就較大，相反地，其他區域的灰度梯度方較小. 如圖6(a)，圖片某一像素點Ii,j的灰度梯度方[10-11]可由其8個鄰域像素點及其自身的光強定義為

(9)

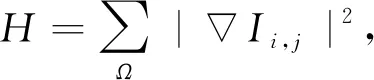
(a)計算Ii,j像素點的平方灰度梯度

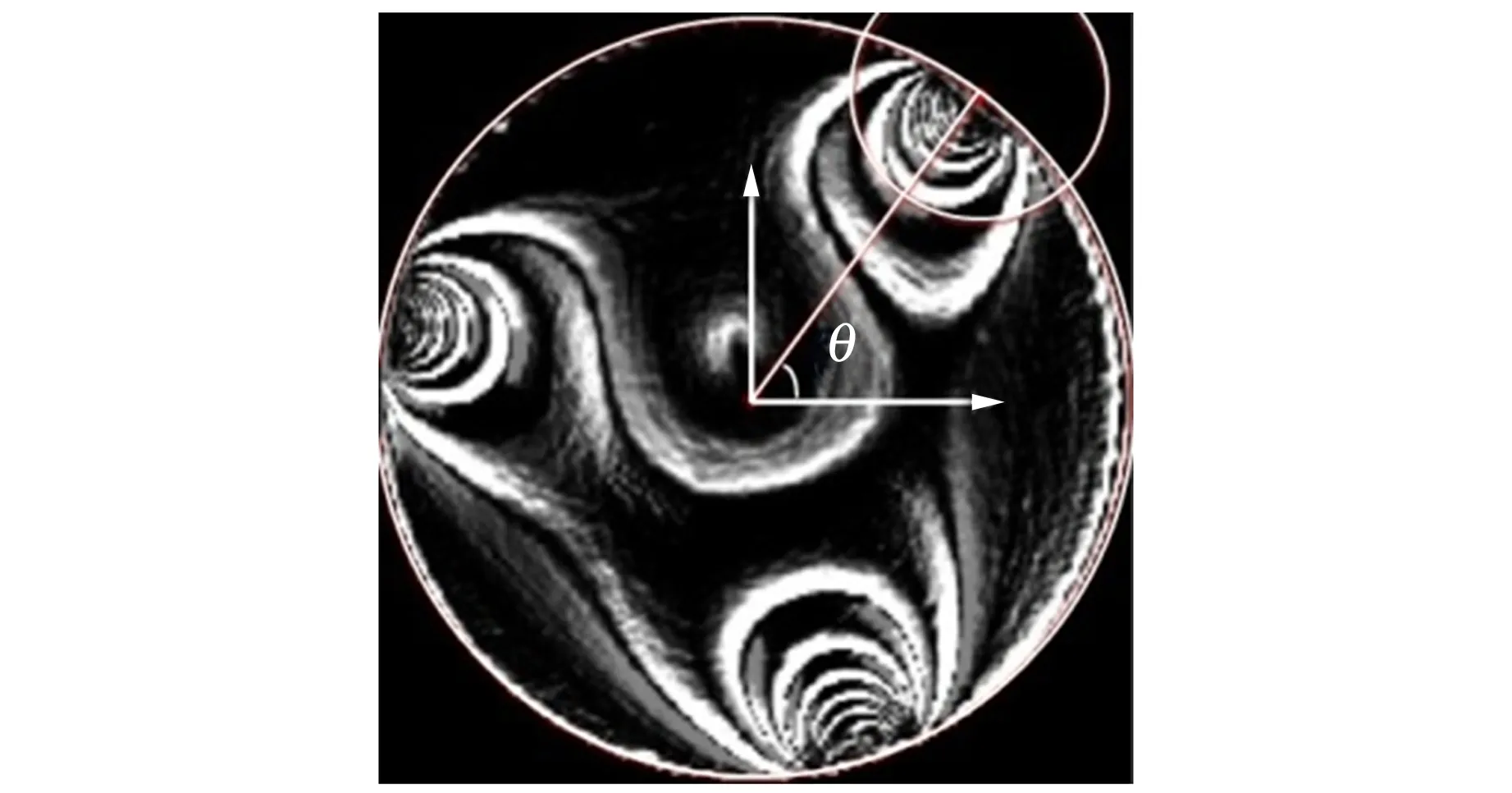
(b)實驗的灰度梯度方分布圖

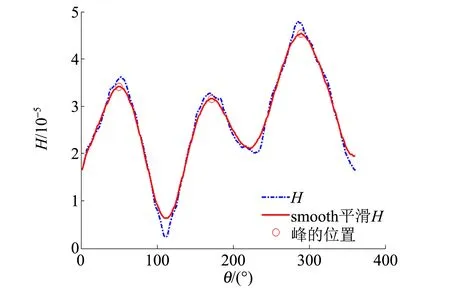
(c)模板內H與θ的關系圖像圖6 邊界圓模板尋找加載點位置的方法

在處理接觸點位置時，發現單單使用邊界圓模板法得到接觸點位置有時會有1°～4°的不確定度，而接觸位置的誤差可能會影響最后處理得到的加載力大小，所以，若顆粒數較多時，采用邊界圓模板法與閾值切割法[11-12]相結合的方法，先采用邊界圓模板法獲得加載點的初步位置，再對應閾值分割法得到的精確位置，如此可結合2種方法的優勢，既不出現對接觸點的誤判，也能保證接觸點位置的精度. 處理單個顆粒或者少量的邊緣處的顆粒時，若想獲得更精確的加載點位置，則需要讓邊界圓模板法獲得的結果再經過人為檢驗來確定更精確的加載點位置.

4 線掃描光強擬合確定接觸力的方法

通過3.2的方法獲取得到加載點位置后, 通過加載圓盤的應力分布的理論可知圓盤內的光強的分布，從而由光強的變化反推出加載力的情況. 然而，對于顆粒的應力光圖，若使用該顆粒全場應力光圖作擬合，計算量與誤差都很大. 接下來只考慮每個加載點到圓心的連線上的光強變化.

4.1 離散坐標系下直線的確定

由于圖片是離散的像素點的灰度值矩陣，要得到加載點到圓心2個像素點的連線的灰度變化，先確定哪些像素點屬于在離散的坐標系中2個像素點之間的“連線”，“連線”實際上是一系列的像素點. 為得到兩像素點之間“連線”，可參考Bresenham算法[13]. 該算法雖然可以得到2個像素點之間的“連線”，但得到的“連線”的“長度”，即找到的像素點的個數，在兩像素點所在直線的斜率為非零有限值時并不合適. 因為顆粒為圓形，那么加載點到圓心2個像素點距離的定義應該按照歐氏距離來定義才較為合理，比如，起點像素點坐標為(10,5)，終點像素點坐標為(40,45)時，“連線”像素點個數按照歐氏距離的定義應該為50個或接近50個，然而使用Bresenham算法得到的“連線”的“長度”為30個或40個.

為了解決這個問題，提出了像素點的逐步行進的方法,如圖7所示，從起點像素點開始，對當前像素點十字4鄰域的像素點進行判斷，判斷滿足以下2個標準的像素點則為下一步需要走的像素點：1)該像素點與起終點之間的理論直線的點線距離最短;2)該像素點與終點的直線距離最短. 注意，如在像素點的十字4鄰域中，某一點為已經走過的點，則需要在判斷時將其略去，這樣逐步行進，即可遍歷2個像素點在二維離散坐標系下的“連線”所對應的像素點，獲得連線的光強變化. 另外，之所以不以像素點的8鄰域進行判斷是由于使用8鄰域判斷出來的兩點間“連線”的長度與實際長度也有較大的誤差，這也是離散坐標系的對于長度的定義與連續坐標系的差異之處.

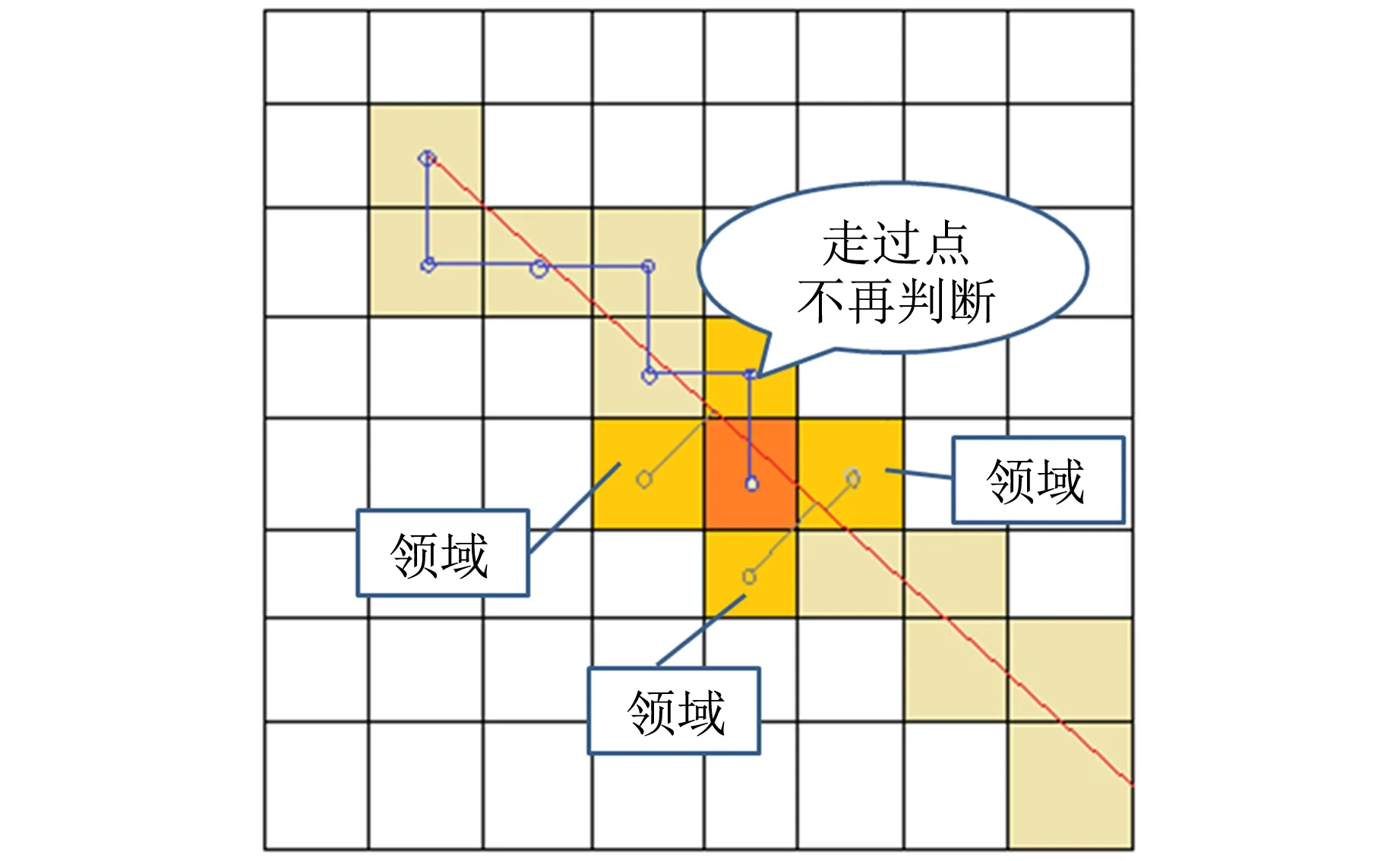
圖7 步行進法示意圖(藍色線為已經走過的像素點)

4.2 線掃描光強變化擬合法

獲取了加載點到圓心連線上的灰度變化如圖8所示，連線上像素點到圓心的距離d=R-r，可以觀察到，灰度變化曲線起伏成峰，在接近加載點位置(左)峰比較密集，在靠近顆粒圓心的位置，峰較為稀疏，實際上這些峰正是反映了連線上各級應力條紋的位置及條紋寬度. 這樣，可以通過與理論對比的結果來反推加載力的大小. 對比實驗中加載點到圓心連線灰度變化的峰的位置與理論的峰的位置，可以觀察知道由于在峰谷與峰頂位置灰度變化不夠平滑，原因是存在噪聲的起伏. 由此，以較為平滑的腰的位置來確定峰的位置.圖片為0～255的灰度級圖片，若以I=Ia/2的光強來決定腰的位置，即以灰度級127確定腰的位置. 另外，灰度級變化以像素點位置離散，如一像素點灰度級為123，下一像素點灰度級為130，在這2個像素點之間，要找灰度級為127對應的位置則需以插值法進行插值找根，由于實驗圖像精度足夠，2個像素點之間直接采用線性插值即可.

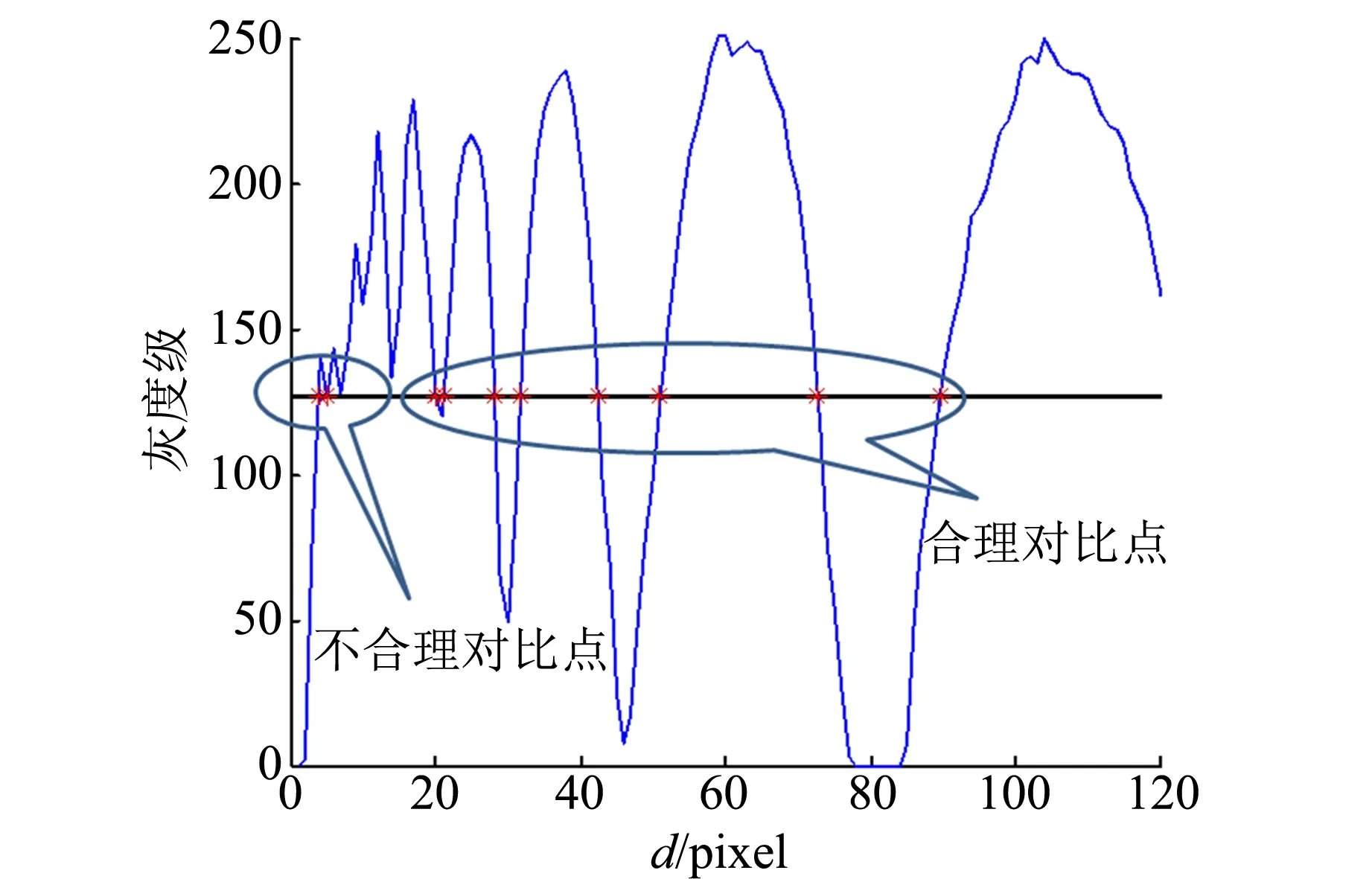
圖8 某一加載點至圓心連線的灰度變化

值得注意的是，這樣處理往往只能得到連線上靠近圓心的一些級數較低的峰的腰的位置. 這是因為實驗中由于顆粒模型存在厚度，發生光的折射，加載點附近的峰的暗條紋不夠明顯，以及拍攝角度問題，在顆粒邊界光強附近會有較大的誤差. 但同樣由于在接觸點附近的條紋均為高級條紋，且理論的灰度變化在靠近加載點附近也奇異，對尋找接觸力意義不大. 在處理時往往只處理低級的條紋，這是可以接受的，且無法避免. 如此獲取了實驗的加載點到圓心連線灰度變化的峰的腰的位置后，這些位置相當1組描述峰的腰的位置的數組向量. 有幾個加載點就會有幾個這樣的向量，將其定義為s(i)，i表示對應的加載點. 同樣的，由顆粒的多點加載光彈性理論，在加載情況下，也可從理論上得到描述加載點到圓心的連線灰度峰的腰的位置的向量. 理論得到的向量的維數往往比實驗得到的向量的維數要多，這是由于由理論可直接得到更多高級的條紋峰的腰的位置. 但是在對比理論和實驗的峰腰位置向量時，需要將理論的向量的維數截取到與實驗的向量維數一致，相當舍棄掉了高級條紋，將這樣處理后得到的峰腰位置向量定義為w(i,Fi)，i代表對應的加載點，Fi為第i個加載點的加載力.

要反推出加載點的加載力大小，接下來讓加載點的加載力Fi在某范圍內變化，計算出每種加載力大小的峰腰的位置數組向量，即計算出一系列的w(i,Fi)，減去實驗對應加載點的峰腰位置向量w(i)，再取其模方，即得到了第i個加載點理論的加載力與實驗的差值的平方. 而每個加載點在某一加載力下都能得到這樣的差值方，對于一種加載情況，以加載點的加載力大小為索引，可建立對應不同加載情況理論與實驗的差值方的i個維度矩陣C，其矩陣的矩陣元表示為C(F1,F2,F3,…，Fi)，i代表第i個加載點，Fi為第i個加載點的加載力，對其數學定義為

(10)

比如加載點數3，每個加載點的加載力的變化以1N為步長，且F∈[10,30]，那么矩陣C為20×20×20的3維矩陣，這個矩陣的最小元素值對應的索引(F1,F2,F3)則為需要的接觸力的大小. 使用矩陣C尋找加載力大小的好處是它對于誤差的包容性，因為理論每個加載力情況的結果與真實實驗結果都存在相同的誤差因子，誤差因子包括：對低級條紋峰的腰位置的錯誤獲取，顆粒應力光圖的灰度級范圍不在0～255. 這些誤差因子有時難以甚至不能抹除，而矩陣C最小元素即對應誤差因子存在時與實驗的差別最小加載情況，也就是所需的最優結果.

通過多點加載二維顆粒實驗，利用線掃描光強變化方法尋找加載力大小的過程如圖9所示.

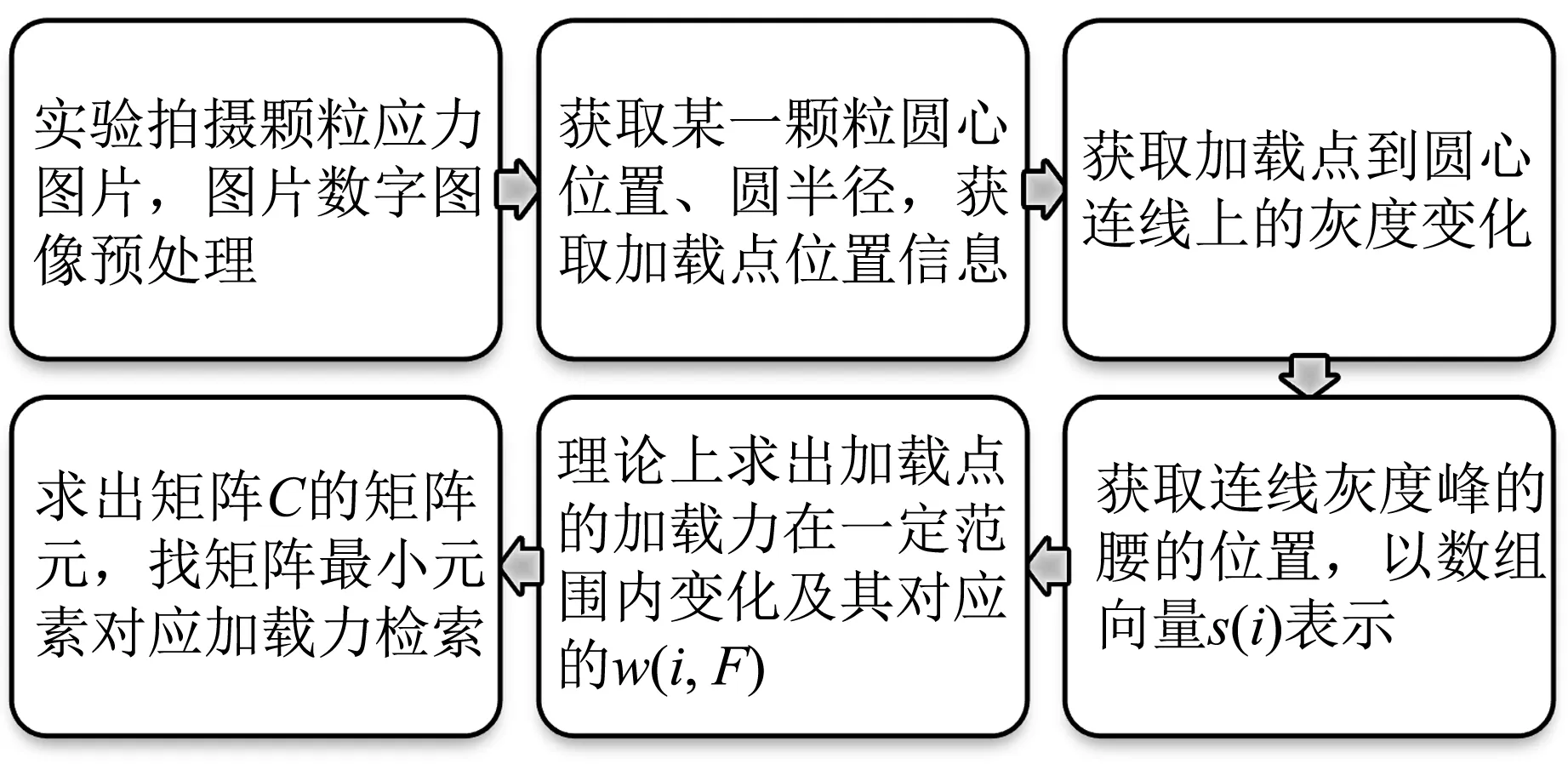
圖9 線掃描方法流程圖

如圖10所示，以3個加載點為例，實驗測得加載力與線掃描光強方法處理得到的加載力對比如表1所示.

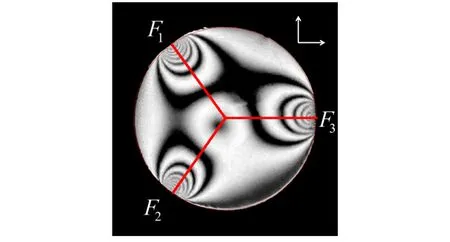
(a)線掃描法獲取連線上灰度變化的示意圖

(b)線掃描法得到的結果模擬圖10 線掃描法獲得連線上灰度變化及模擬結果

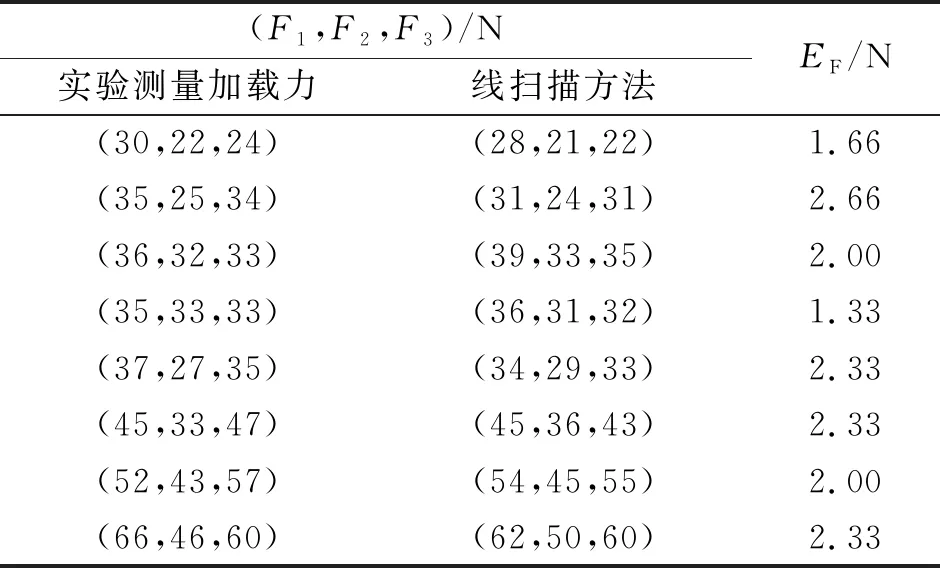
表1 3點加載力對比表

將線掃描方法處理得到的加載力大小反過來模擬出顆粒的應力光圖,如圖10(b)所示，可以看出與實驗圖案圖10(a)相比還是有所區別，這是由于實際實驗中模型受加載后發生形變，加載處的加載方式已經由線接觸變為了面接觸，這也是通過先掃描的方式來尋找加載力的大小的原因. 如果對顆粒上全場的光強來考慮，一是由于3維圓柱顆粒的線與面接觸方式不同帶來的應力光圖的差異帶來的誤差在考慮全場的光強時會更大；二是顆粒邊界處的光強由于折射拍攝角度等帶來的誤差也難以處理；三是計算量較大. 但考慮顆粒上的全場光強的方法也有一定好處，即可以處理更加復雜加載情況下的圖案. 要靠這種方式來尋找加載力大小，先讓計算機進行預處理再人工調節尋找加載力大小，通過計算機與人的相互協作的方式反而更簡單.

5 結束語

基于顆粒應力光圖的灰度梯度平方分布圖像的邊界模板法可以獲取顆粒的接觸點位置. 該方法優點是能夠在光彈顆粒條紋不十分密集的情況下，找出在顆粒邊界處有較大的加載力存在的加載點的位置. 其缺點是不能夠適用過于密集的顆粒應力條紋光圖，且處理得到的加載點位置可能存在1°～4°的不確定度. 如果在大量顆粒接觸時，可采用該方法與閾值切割方法[12]結合的思路. 在離散坐標系下尋找2點之間“連線”的算法，能夠更加優化地處理Bresenham算法得到的“連線”的像素點個數在2點斜率在為非零有限值時不合適的問題. 基于對顆粒應力光圖的線掃描的獲取接觸力大小方法，結合了二維顆粒多點接觸的光彈性理論、數字圖像處理，能夠得到顆粒每一接觸點的較為精確的接觸力的大小. 為了提高該方法的運行速度與處理精度，應該事先確定顆粒上的加載力合理的模擬的范圍，可采用平均灰度梯度方的方法得到顆粒的平均加載力以確定加載力的范圍.