利用圓巧解題

俞新龍

因為圓在初中平面幾何中有較多的涉及，在高中數學中又有圓錐曲線壓身，所以圓的身份比較尷尬：想被重視卻重視不起來，從而導致一些能用圓巧妙解決的較難問題無法被有效突破. 本文舉例說明.

一、尋找向量中圓的身影，有效突破最值

向量作為高考必考的知識點已經成為高考命題者嘗試創新命題的一個重要陣地，近年來在高考和各省市模擬卷中出現了不少有新意的考題，其中有一些考題若能挖掘出題中隱含的“圓”，則問題便能較好的求解.我們知道向量是數形結合體，故一般向量問題都會有兩種解決辦法：代數法和幾何法.下面我們就從這兩個方面來進行求解.

例1. 已知■，■，■是平面向量，■是單位向量.若非零向量■與■的夾角為■，向量b滿足■-4■·■+3=0，則|■-■|的最小值是（ ）

A. ■-1B. ■+1C. 2D. 2-■

解析：

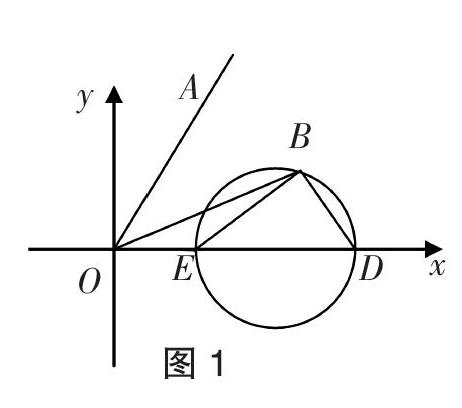
代數法（坐標法）：如圖1建立平面直角坐標系，設■=■=（1，0），■=■，■=■=（x，y），則可知A在射線y=■x（x>0）上，又根據等式■-4■·■+3=0可得（x-2）2+y2=1，所以知B在以（2，0）為圓心、1為半徑的圓上. |■-■|的幾何意義是線段AB的距離，即圓（x-2）2+y2=1上任意一點與射線y=■x（x>0）上任意一點的距離，故|■-■|的最小值顯然是圓心（2，0）到射線y=■x（x>0）的距離■減去圓半徑1，故答案為A.

幾何法：因為■-4■·■+3=■-4■·■+3■=（■-■）·（■-3■）=0，所以BE⊥BD，如圖1所示，則可知B在以ED為直徑的圓上，即得B的軌跡為（x-2）2+y2=1，其余做法同代數法，略.

評注：代數法中的圓從方程中能夠直觀得到，但幾何法中的圓需要結合直角三角形直角頂點一定在以斜邊為直徑的圓上這個性質.

例2. 已知平面向量■，■，■滿足|■|=4，■·（■-■）=■·（■-■）=3，當■與■的夾角最大時，■·■=________.

解析：設■=■=（4，0），

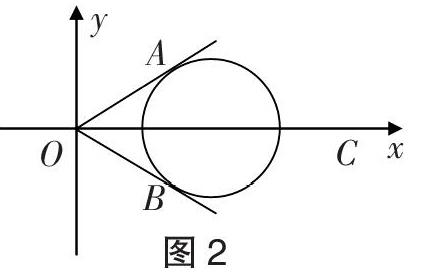
代數法（坐標法）：設■=■=（x，y），則根據■·（■-■）=3得x（4-x）+y（-y）=3，化簡得（x-2）2+y2=1，即向量■終點A在（2，0）為圓心、1為半徑的圓上，同理■終點B也在（2，0）為圓心、1為半徑的圓上，如圖2所示OA、OB與圓相切時向量■與■的夾角最大，此時A（■，■），B（■，-■），所以■·■=■-■=■.

幾何法：由條件等式■·（■-■）=■·（■-■）=3整理得（■-■）2=（■-■）2=1，即知向量■與■是（2，0）為圓心、1為半徑的圓上的兩個動點，記■=■，■=■，如圖2所示OA、OB與圓相切時向量■與■的夾角最大，此時A（■，■），B（■，-■），所以■·■=■-■=■.

評注：配方是個難點，從配方式子中看出軌跡是圓是關鍵點.

例3. 已知非零向量■，■，■，滿足|■|=2，■·■=■|■|，■=■■·■-2，則對任意實數t，|■-t■|的最小值為___________.

解析：設■=■=（2，0），根據條件■·■=■|■|知向量■、■的夾角為30°.

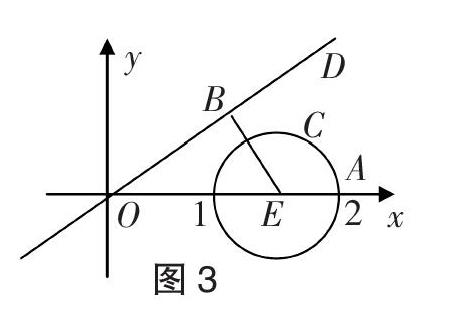
代數法（坐標法）：設■=■=（x， y），則根據■=■■·■-2得x2+y2=3x-2，化簡得（x-■）2+y2=■，如圖3所示，點B在直線OD：y=■x上運動，點C在以E（■， 0）為圓心、■為半徑的圓上運動，因為 | ■-t■ | 的幾何意義是圓E上的任意一點到直線OD上的任意一點的距離，故 | ■-t■ | 的最小值為圓心E到直線OD的距離減去圓半徑■，即■-■=■.

幾何法：由■=■■·■-2得2■=3■·■-4=3■·■-■，從而得（2■-■）（■-■）=0，如圖4所示，■=■，2■=■，則2■-■=■，■-■=■，所以■⊥■，又FC1//AC2，所以FC1⊥AC2，因此，向量■的終點C1在以AF為直徑的圓上. 下同，略.

評注：本題幾何法找向量的終點需要進行平行轉化，具有一定的難度.

二、尋找阿波羅尼斯圓的身影，有效突破最值

若 A（a， 0）， B（0， 0），若 | PA |2=k2 | PB |2（k≠1），則（x-a）2+y2= k2（x2+y2），化簡得（x+■）2+y2 = （■）2，故P點軌跡是圓心在AB上且半徑為 |■| 的圓. 這個軌跡最先是由古希臘數學家阿波羅尼斯發現，簡稱阿氏圓. 阿氏圓能化身各種形態存在于問題中，需要我們去發現其身影.

例4. 已知■，■是平面內兩個互相垂直的單位向量，若向量■滿足 | ■-■ |=■，則 | ■+■-■ |+2| ■-■ | 的最小值為________.

解析：如圖5，以■=■，■=■，則 |■+■-■? |+2|■-■ |=CD+2CB，設C（x， y），由 | ■- ■ |=■得（x-1）2+y2=■，則根據阿波羅尼斯圓知可在AD上找一點E（1， m）使CD=2CE，即■= 2■，化簡得x2-2x+y2-■y+■=0，此方程與點C軌跡方程是一樣的，則■=0，■=■，解得E（1，■），則 | ■+■-■ |+2| ■-■ |=2CE+2CB≥2BE，故 | ■+■-■ |+2| ■-■ |≥■.

評注：阿波羅尼斯圓的正用不難，難的是逆用甚至變用，一般求兩條比例為1：λ（λ≠1）的線段和就可以試著用阿波羅尼斯圓的性質進行求解.

例5. 已知A，B是平面上的兩個定點，平面上的動點C，D滿足■=■=k，若對于任意的k≥3，不等式λ≥■恒成立，求實數λ的最小值.

解析：如前所述，阿波羅尼斯圓半徑r= |■|=■，即只與兩個定點間距離和比值有關. 根據本題條件■=■=k可知，點C、D同在由A、B、k確定的阿波羅尼斯圓上，故CD的最大值就是直徑為■，于是■=■，又由于k≥3，所以■=■=■，易知y=■在k≥3上是減函數，故■有最大值■. 根據λ≥■恒成立得λ≥■.

評注：巧妙利用阿氏圓半徑，將問題化為函數單調性問題確實事半功倍.

例6. 已知兩個不共線的向量■，■，滿足 | ■ | =3，| ■+■ | =2|■-■ |，設■，■的夾角為？茲，求cos？茲的最小值.

解析：本題用阿波羅尼斯圓來解答的難點在如何根據條件 | ■+■ | =2|■-■ | 來構造？

記■=■=■，■=■，則■ =■+■，■=■-■，故 | AP | = 2 | CP | ，因此，P在以 | AC | =6、k=2的阿波羅尼斯圓O上. 如圖6所示，圓半徑r=■=4，因為？茲=∠PBC，所以易知當BP與圓O相切時？茲最大，此時cos？茲取到最小值.

根據等量關系可以求出CO=2，所以BO=5，故相切時可求得BP=3，此時cos？茲=■，所以cos？茲的最小值為■.

評注：從■+ ■、■- ■不難聯想到平行四邊形，所以可以先用平行四邊形對角線性質解題，即|■+ ■ |2+|■- ■ |2=2（|■|2+| ■ |2）=5|■- ■|2，化簡得| ■ |2-10cos？茲| ■ | +9=0，由該方程有解得△=100cos？茲2-36≥0，解得| cos？茲 |≥■. 根據|■+ ■|=2|■- ■|可知■，■的夾角？茲為銳角，所以cos？茲≥■.

三、利用直徑與圓內外點所成角，有效突破范圍

我們知道，圓上的點與直徑兩端成直角，圓內的點與直徑兩端成鈍角，圓外的點與直徑兩端成銳角，在解題時一定要有效用起來，以達到突破問題的效果.

例7. 已知圓O：x2+y2=4，A、B為圓上兩個動點，滿足|AB|=2■，D為線段AB的中點，E（3，m），F（3，m+5）. 當A、B在圓上運動時，存在某個位置使∠EDF為鈍角，則實數m的取值范圍是_________.

解析：如圖7，因為弦長|AB|=2■，所以根據垂徑定理知圓心距|OD|=1，所以點D的軌跡方程為x2+y2=1. 當A、B在圓上運動時，存在某個位置使∠EDF為鈍角，等價于當D點在圓上運動時，存在位于以AB為直徑的圓內的時候. 記AB中點M（3，m+■），則|DM|<■有解，故|DM|min<■. 而|DM|min=|OM|-1=■-1，解得 -■

評注：存在某個位置問題轉化為距離的大小關系問題，顯然將問題的難度大大降低了.

責任編輯 徐國堅