初邊值條件對二維通道內降膜流動行為影響的數值分析

杜卡帥，胡珀，胡真，翟書偉

上海交通大學 核科學與工程學院，上海 200240

非能動安全殼冷卻技術（passive containment cooling system, PCCS）主要依靠水膜的蒸發換熱以及逆流空氣的自然對流等共同作用，將反應堆在發生事故過程中產生的熱量排出到環境中。為了保證安全殼有足夠的冷卻能力，需要對水膜在逆向空氣剪切力作用下的降膜流動規律有比較深刻的認識，進而為CAP1400 的PCCS 系統設計提供理論支撐。

由于PCCS 結構為尺寸較大的雙層圓柱罐體，因此可簡化為大尺度矩形通道。眾多學者采用實驗[1-3]和數值[4-5]方法研究矩形通道內的降膜流動特性，包括降膜厚度、降膜覆蓋寬度、降膜表面波形態、降膜表面波波速以及降膜流動的演變過程。但是在這些研究中，主要考慮水膜的流動，而忽略了空氣和液膜相界面的剪切力。Huang等[6]指出在較大速度的逆向空氣氣流作用下，降膜流動會受到破壞，出現液滴夾帶的現象。為克服試驗研究中僅能獲取局部位置的液膜參數信息，采用數值模擬手段來解決。但是在模擬過程中，水膜通常被假定為定常層流流動，忽略其表面波動。目前普遍認為即使再小的液膜雷諾數，也會發生波動，暫時沒有波動出現可能是由于在降膜流動中平板傾角過小，或者研究中的流動距離過短等原因造成的[7]。田瑞峰等[8]在對水膜表面進行受力分析的基礎上，建立二維板壁水膜波動流動模型，并討論了液膜入口擾動頻率以及擾動振幅對降膜波動情況的影響。黃磊等[9]在研究板式海水淡化降膜吸收裝置時，建立三維平板降膜流動數值模型，考慮了氣液剪切力作用；但是他們研究的計算域尺寸較小，尤其在降膜流動方向上。就現有相關研究工作而言，降膜流動方向上的長度最多為厚度方向的200 倍[4]。盧濤等[10]研究表明在降膜流動過程中，同一高度處的液膜厚度差別不大。另外，在實際PCCS 系統內，水膜流量隨著重力水箱液位的下降而不斷減小，在鋼制安全殼壁面上形成的水膜厚度也逐漸減薄，水膜厚度占整個通道高度尺寸的比例是變化的。

因此，在文獻[10-11]基礎上，考慮空氣和液膜相界面剪切力，建立二維單側矩形通道降膜流動的數值模型，其中入口水膜寬度也被當作水膜在入口位置的厚度。為使降膜流動充分發展，同時盡量減少計算域中劃分的網格數量，需先將PCCS 環形通道的實際高度進行縮小；接著采用固定通道高度而改變液膜入口寬度的辦法，分析通道高度對水膜厚度沿流動方向變化的影響。此外，還考察不同邊界條件（液膜入口速度分布、液膜入口雷諾數、空氣入口速度以及空氣流動方向等）對液膜形態以及液膜平均厚度變化的影響，為進一步分析PCCS 系統降膜蒸發傳熱傳質特性提供基礎。

1 模型及求解方法

1.1 物理對象描述

如圖1 所示，PCCS 流道被簡化成一個高度為25 mm（x軸，即降膜厚度），長度為800 mm（y軸）的二維矩形通道，流動介質為水和空氣。水膜在重力作用下始終沿固體壁面（鋼制大平板）由上而下形成降膜流動，而空氣則以一定的速度從入口位置進入計算域，跟水膜形成并流（圖1（a））和逆流（圖1（b））2 種情形。水膜和空氣的相交界面將整個通道的高度分成2 部分，采用3 個不同的水膜入口寬度（分別為1、3、5 mm），以研究水膜入口寬度對降膜流動行為的影響。

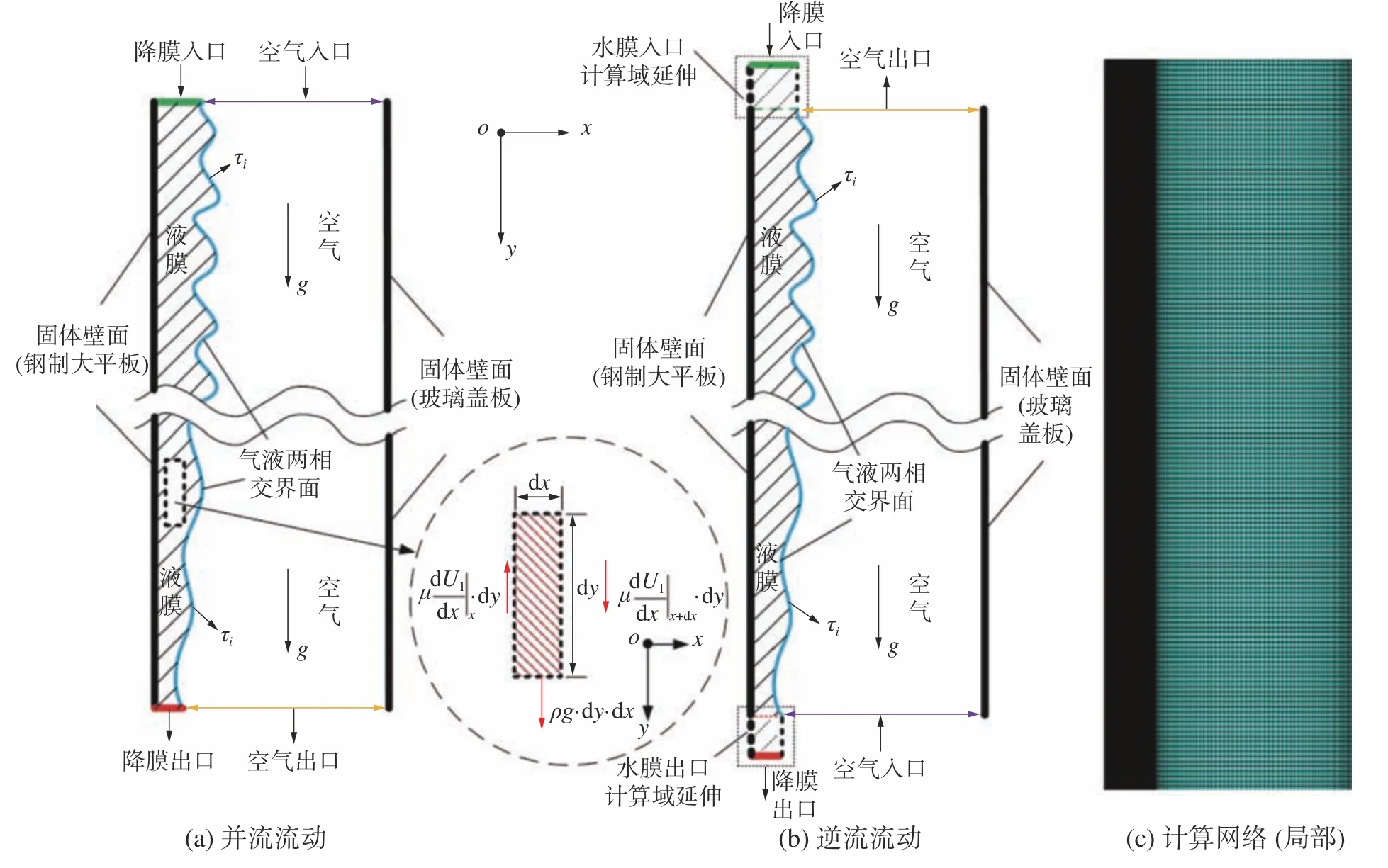
圖1 物理模型及數值計算網格

液膜和空氣的進口設置為速度入口；液膜和空氣的出口設置為壓力出口；左側接觸水膜的鋼制大平板設置為無滑移壁面，接觸角為45°；而右側玻璃蓋板也設置為無滑移壁面，接觸角為90°。空氣的入口指定為均勻速度，而液膜的入口有均勻入口、準對數分布、對數分布3 種方式，如圖2所示。其中圖2（b）、（c）的邊界條件通過Fluent用戶自定義函數（UDF）實現。整個計算域的初始速度為0，只有緊貼鋼制大平板壁面的一薄層區域設置為水膜，該薄層厚度可由式（1）確定，其余部分均為空氣：

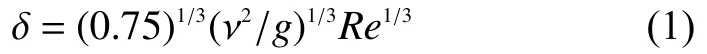
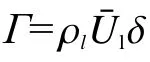
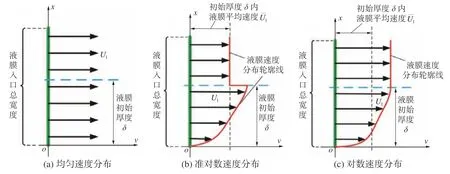
圖2 液膜入口速度分布示意

另外，本文中液膜雷諾數和空氣流速等參數范圍主要依據文獻[12]進行選取。

1.2 數值求解

采用計算流體力學軟件Fluent15.0 研究空氣剪切力作用下垂直鋼板表面水膜流動行為。其中空氣和水膜兩相界面通過幾何重構兩相流模型——流體體積函數（volume of fluid，VOF）捕捉，同時耦合連續表面張力（continuum surface force，CSF）模型求解表面張力；湍流模型選擇可實現的k-ε模型，并采用增強近壁面處理方法。氣液界面剪切力τi根據式（2）確定，通過UDF 實現：

式中： ρg為空氣的密度；ug為空氣的入口流速；f為兩相摩擦阻力系數，可根據Wallis[13]（并流）和Stephan[14]（逆流）曳力系數模型求解：

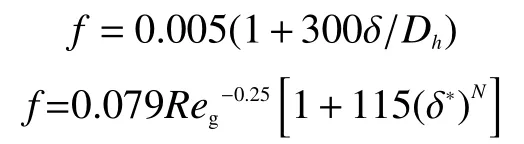
式中：δ*=δ/LL；N=3.95/[1.8+3(LL/Dh)] ；LL=[(ρl-ρg)g/σ]-0.5；σ為氣液兩相之間的表面張力系數；Dh為水力直徑。

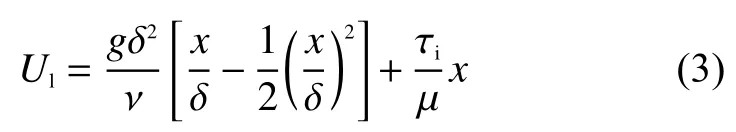
采用基于壓力的瞬態求解器，為提高解的收斂性，開啟隱式體積力選項。時間項采用一階隱式格式，動量和湍流項采用二階迎風離散，壓力項采用PRESTO 算法，壓力和速度的耦合方式選擇PISO 方法。質量、動量及湍流等控制方程迭代殘差的收斂標準設為10-4。時間步長設為10-4s，總模擬時間為1.0 s。當空氣和水膜逆流流動時，為了防止水膜直接從氣相出口流出，對計算域中水膜入口和出口位置進行延伸，延長的長度均為100 mm，同時計算過程改為穩態計算。

由于降膜流動瞬態發展過程中的平均液膜厚度是一個非常關鍵的參數，該參數決定了降膜流動傳熱傳質的阻力。因此，本文主要對流動穩定階段的液膜厚度進行統計，具體按下式進行計算

式中n為流動穩定區域沿流動方向的網格節點總數。

1.3 網格無關性分析及數值模型驗證

采用分區劃分網格的方法，對液膜區域進行加密，選擇結構化網格，如圖1（c）所示，網格在x方向上的分布是不均勻的，尤其是靠近氣液相交界面以及壁面的地方，網格較密集。使用3 種不同數量網格，最小網格尺寸分別為0.05、0.1、0.2 mm（對應網格總數量為43 萬、26 萬、14 萬），以液膜雷諾數Rel=300（均勻入口速度）、空氣雷諾數Reg=0、液膜入口寬度為5 mm 的工況進行網格無關性分析。提取網格單元中液體體積份額等于0.5 時所對應的x坐標值作為液膜厚度。從圖3看出，當網格總數為26 萬和43 萬時，水膜厚度隨流動方向的變化趨勢是一致的，即沿著降膜流動方向，液膜厚度越來越小，最大偏差不超過4%。因此，為節約計算成本，本文選擇網格總數量為26 萬的模型進行模擬。

圖3 網格無關性分析

為驗證該數值模型有效性，選擇文獻[11]中的工況進行比較，主要參數為：Rel=750（均勻入口速度）、Reg=0、入口寬度為1 mm。從圖4 看出，本文所計算的液膜厚度沿流動方向的變化趨勢跟文獻預測結果是比較吻合的，當流動距離超過0.5 m后，降膜的波動頻率和波動幅值都很接近，該段流動距離內液膜平均厚度的最大偏差不超過8%。由此可見，本文所建的數值模型是合理的。

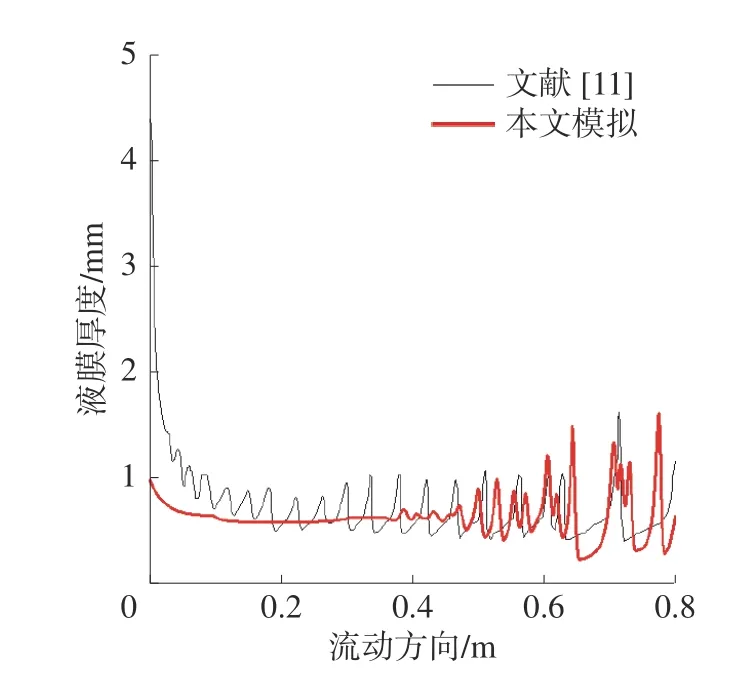
圖4 數值模型驗證

2 模擬結果與分析

2.1 入口速度分布影響

圖5 為3 種不同入口速度分布條件下鋼板表面水膜厚度沿流動方向的變化情況，其中水膜入口寬度5 mm，空氣雷諾數為0，液膜雷諾數分別為300、900、1 500、2 700。

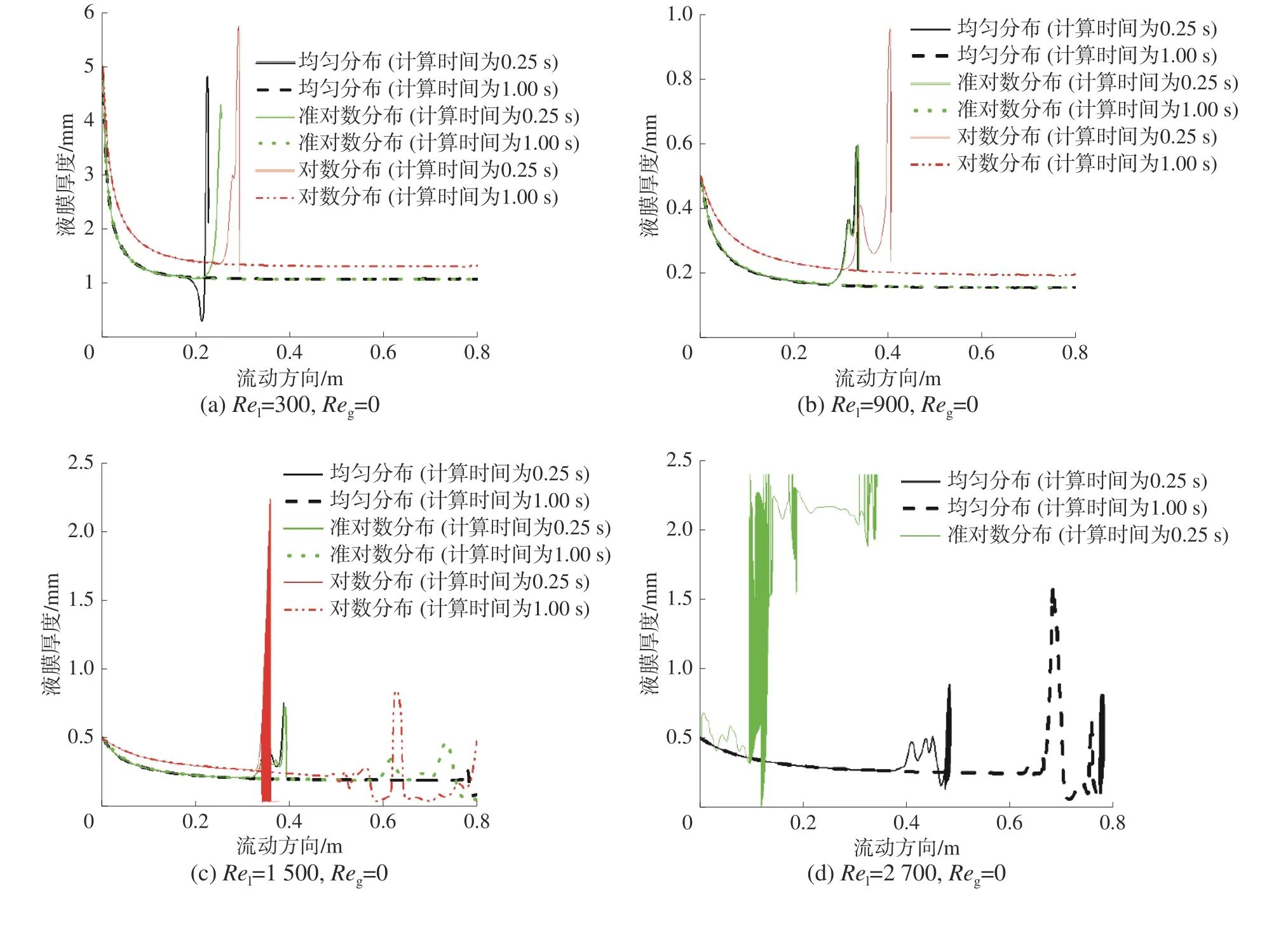
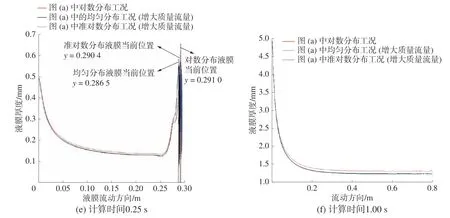
圖 5 入口速度分布對液膜厚度沿流動方向變化的影響

從圖5（a）～（d）看出，當計算時間為0.25 s 時，液膜在均勻分布條件下流動最慢，而在對數分布條件下流動最快；而當計算時間為1.0 s 時，液膜厚度沿流動方向的變化趨勢處于穩定，并且在均勻和準對數2 種分布條件下液膜厚度的變化規律是重合的，液膜厚度均小于對數速度分布條件下的數值。這主要與液膜入口質量流量有關。從圖2 可知，在均勻分布和準對數分布條件下，液膜入口質量流量是相等的，并且小于對數分布條件下的值。另外，當液膜入口雷諾數在300～1 500 遞增時，準對數分布和均勻分布條件下液膜y方向流動速度差值在不斷減少，甚至超過液膜在對數分布條件下y向的流動速度，如圖5（c）所示。這是由于液膜產生較明顯的x方向的流動速度，引起表面波動增強，進而使y向的流動速度減小。如果液膜雷諾數繼續增大，將產生如圖5（d）中所示的液膜“托舉”現象，導致大部分液膜脫離鋼板壁面而沿對側玻璃壁面流動。尹涌瀾[15]認為液膜在重力作用下聚集使其前段速度大于下部的氣相速度，導致液膜產生偏轉。

此外，在相同的液膜入口寬度條件下，入口速度分布的影響作用可能被放大，因為還受到液膜入口質量流量的影響。從圖2 可知，需增大均勻和準對數分布中液膜入口寬度方向上的液膜入口速度，或者減小對數分布中液膜入口寬度方向上的液膜入口速度，從而保證均勻、準對數以及對數分布這3 個工況具有相同的液膜入口質量流量，這樣也就更能評估入口速度分布的影響。圖5（e）和（f）中均勻和準對數分布算例增加了液膜入口寬度方向上的液膜入口速度，從而保證圖5（e）和（f）中的均勻、準對數和對數分布中液膜具有相同的入口質量流量，都等于圖5（a）中對數分布工況下的值。分析圖5（e）、（f）中數據可知，對數分布和均勻分布對平均液膜厚度產生的影響在8% 以內，要小于圖5（a）中對數和均勻分布的影響（約22%）；而圖5（e）、（f）和圖5（a）中準對數分布和均勻分布對平均液膜厚度產生的影響均小于1%。另外，在圖5（c）看到，當液膜雷諾數增大到1 500 時，準對數分布和均勻分布對平均液膜厚度產生的影響將變大（接近5%）。我們比較液膜波動出現的位置、頻率以及產生的波幅，發現液膜波動現象在準對數分布條件下比在均勻條件下明顯。

綜上所述，速度分布對液膜厚度變化規律的影響主要是通過液膜入口質量流量變化來反映。如果液膜入口寬度越小，越接近經典的Nusselt 值，那么速度分布對液膜厚度變化規律的影響可忽略不計。

2.2 液膜入口寬度的影響

圖6 為3 種不同水膜入口寬度（1、3、5 mm）下水膜厚度沿流動方向的變化情況，其中液膜和空氣的雷諾數分別為300 和0，水膜入口速度為準對數分布。當降膜流動時間為0.25 s 時，液膜沿y方向的流動速度隨液膜入口寬度的減小而增加，而最大液膜厚度卻隨入口寬度的增加而增加。可見，液膜在較小的入口寬度下主要表現出沿通道長度方向上的鋪展流動，此時，對應的液膜厚度較薄，所受黏性力作用較弱。隨著液膜入口寬度的增加，液膜在x方向的堆積作用增強，導致液膜明顯增厚，所受的黏性力也逐漸增加。因此，當流動時間增至1.0 s時，流動已處于穩定，液膜表面在入口寬度為3、5 mm 時比較平坦，而在1 mm 時則呈現出波動。另外，根據式（4），很容易得到跟文獻[10] 相同的結論，即液膜平均厚度隨入口寬度增大而增大。

圖6 液膜入口寬度對液膜厚度沿流動方向變化的影響

2.3 空氣入口流速及液膜入口雷諾數的影響

設計4 組空氣和水膜并流流動計算工況，關鍵參數見表1，相應的計算結果如圖7 所示。

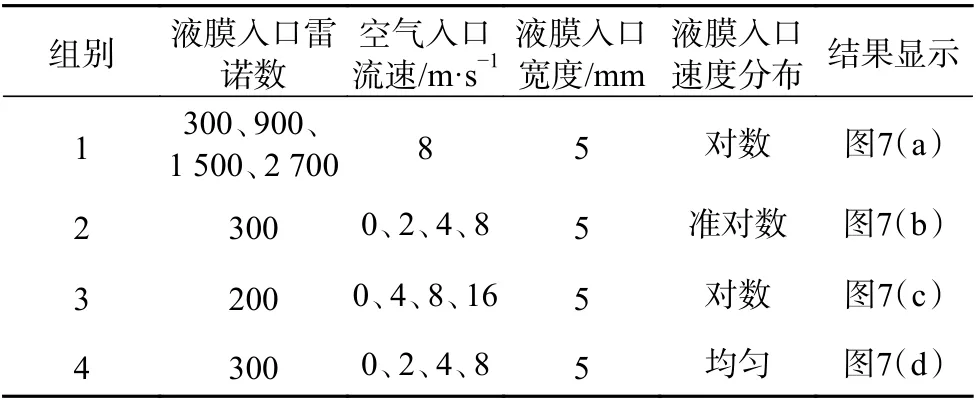
表1 數值計算工況關鍵參數

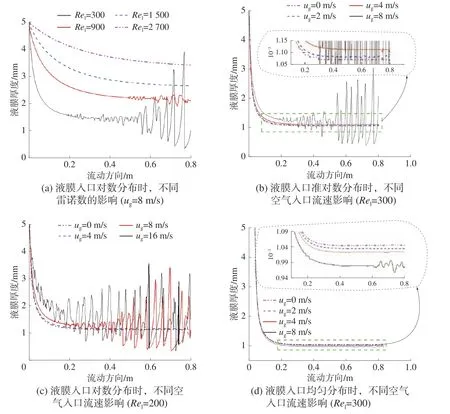
圖 7 空氣入口流速及液膜入口雷諾數對液膜厚度沿流動方向變化曲線(液膜入口寬度5 mm)

圖7（a）主要描述了液膜入口雷諾數的影響，從該圖可知，在液膜入口寬度為5 mm，并流空氣流速為8 m/s 時，隨著液膜入口雷諾數的增加，液膜平均厚度在不斷增加，這與自由降膜流動條件下（圖5）得到的結論是一致的。但也有不同的地方，特別是液膜表面的波動情況。在自由降膜流動條件下，液膜表面波動表現出隨液膜入口質量流量增加而增強的狀態；然而，在較大的空氣剪切力作用下，隨液膜雷諾數增加，液膜表面的波動是逐漸減弱的，甚至消失。這是因為當空氣入口流速固定不變時，液膜表面的流動速度隨液膜入口質量流量的增加而增加，從而導致了氣液兩相之間的速度差減小，因此，在較高的液膜雷諾數下，液膜表面波動不斷減弱。

圖7（b）～（d）主要展示了空氣入口流速的影響，從圖7（b）、（c）中均能看出，液膜表面波動隨著空氣入口流速的增加而顯著增強，這與空氣和水膜兩相之間的速度差有關。然而，平均液膜厚度隨氣流速度增加而增加，這與盧濤等[10]得出液膜平均厚度隨氣流速度增加而減薄的結論相悖，主要是由邊界條件不同所引起的。據式（3）可推知，圖7（b）、（c）中的液膜質量流量是在文獻[10]的基礎上疊加了氣液波動界面剪切力作用而引起液膜質量流量變化。另外，圖7（d）中的結果是在保證液膜入口總的質量流量不變的條件下得出的，相當于僅考慮式（3）右邊第一項的影響。從圖7（d）中也恰好發現液膜平均厚度隨氣流速度增加而減小。因此，當ug增大時，首先，根據式（2）計算，τi會逐漸增大；接著，由式（3）計算Ul的平均值也會增加。在相同的液膜入口寬度條件下，總的液膜質量流量增加，所以，圖7（b）、（c）中液膜平均厚度隨氣流增加而變大。但是Ul的增加值相對于ug而言是比較小的。那么，兩相間的速度差就會隨空氣流速的增大而增大，液膜的波動現象就會變得強烈。在圖7（d）中也發現液膜波動隨空氣流速的增大而增大，但波動幅度明顯小于圖7（b）、（c）。

此外，由于液膜表面流動速度隨液膜入口雷諾數的減少而減慢，當液膜雷諾數減少至200 時，液膜在1.0 s 還沒抵達通道出口位置，所以實際計算的流動時間取2.0 s。

2.4 氣體流動方向的影響

圖8 為液膜入口寬度為5 mm，雷諾數為900，空氣入口速度分別為0、1、2 m/s 時，氣體流動方向對液膜厚度沿流動方向變化的影響。由圖8 可知，空氣流動方向對液膜厚度沿流動方向的變化影響較大，即在逆流條件下，液膜表面處于波動狀態，并且平均液膜厚度要比并流條件下的大。這種影響在較大的逆向空氣流速條件下會更加明顯。因為剪切力τi與氣流速度ug2相關，且隨氣流速度增加而增加，它迫使液膜在逆流條件下做減速運動，而在并流條件下做加速運動。另外，在圖8（a）中得到和圖5（b）相同的結果，即并流液膜厚度在對數分布條件下要比準對數分布以及均勻分布條件下的大。但是在逆流情況下，如圖8（b）所示，對數分布條件下液膜平均厚度跟準對數條件下的差值在逐漸減少，準對數條件下的液膜平均厚度比均勻條件下的小，主要原因是剪切力τi在逆流條件下為負值。

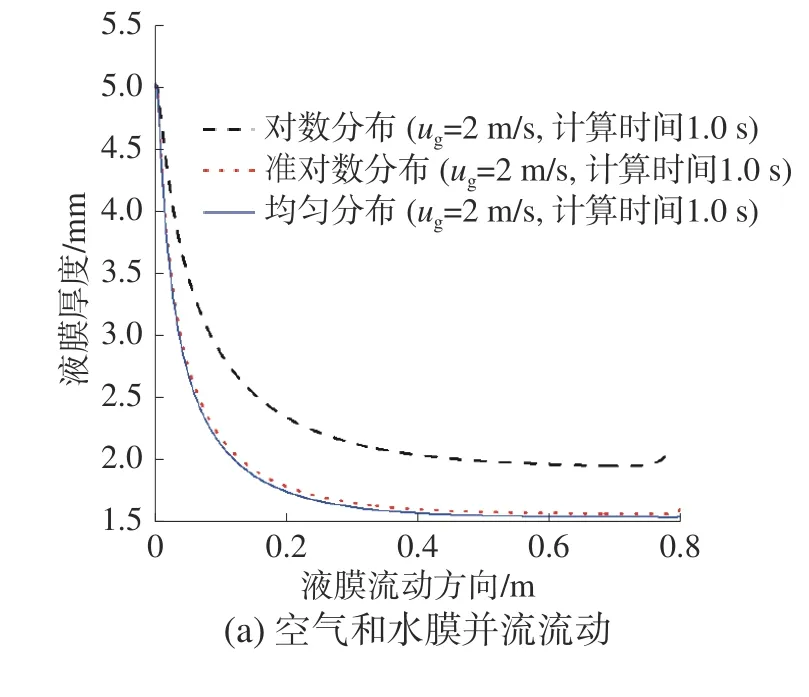
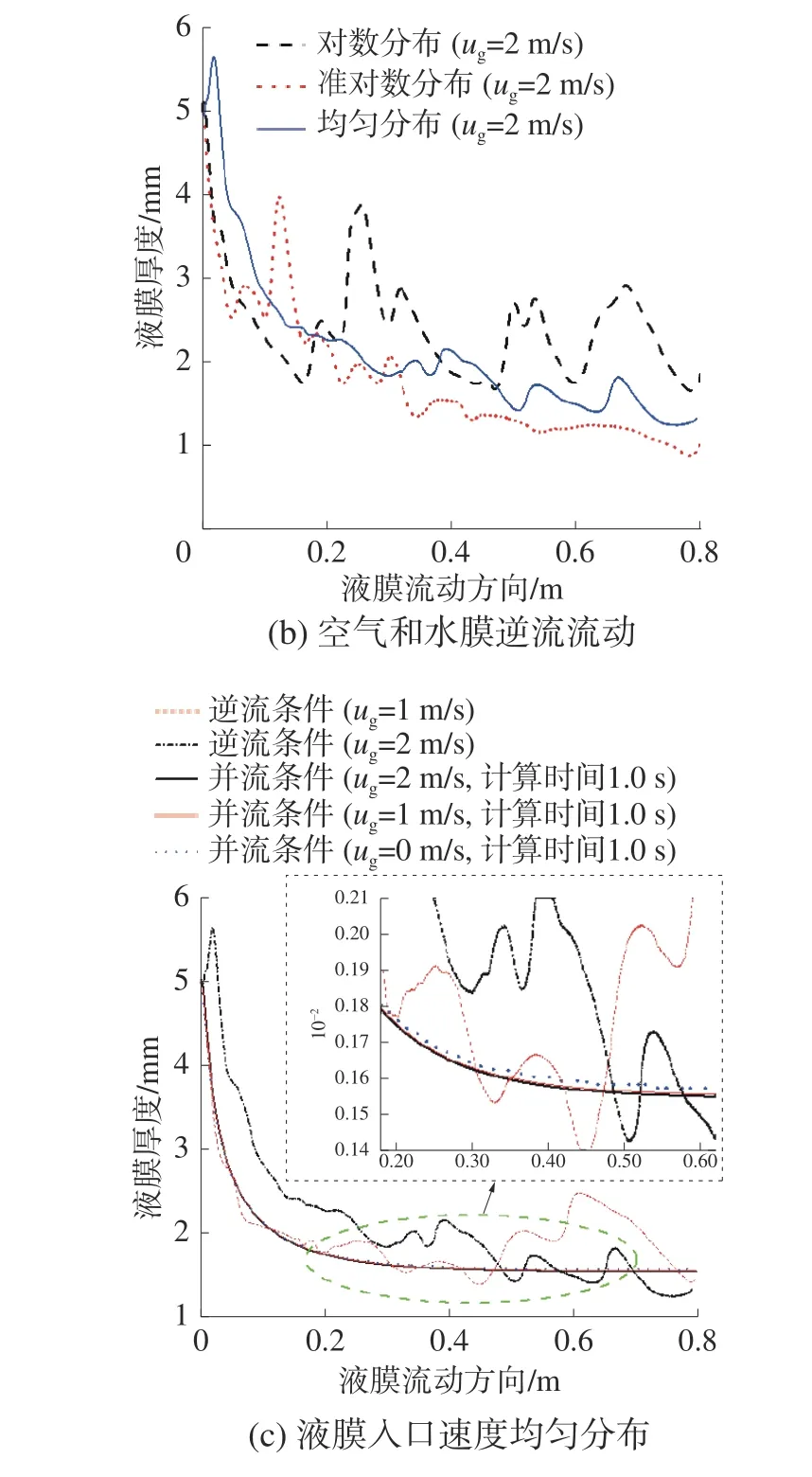
圖8 空氣流動方向對液膜厚度沿流動方向變化的影響

圖9 為平均液膜厚度在液膜入口寬度為5 mm、雷諾數為900 和1 500 時隨氣流速度的變化，從圖9 中看出，不同入口條件下液膜平均厚度隨入口空氣流速的變化趨勢是完全相同的，并且液膜雷諾數較大時，液膜的平均厚度也會越大。另外，還給出理論預測值（基于Nusselt 液膜平均厚度，詳細推導方法參見文獻[12]），結果表明理論預測值和CFD 計算結果的變化趨勢相同，但理論預測值明顯小于CFD 計算值。

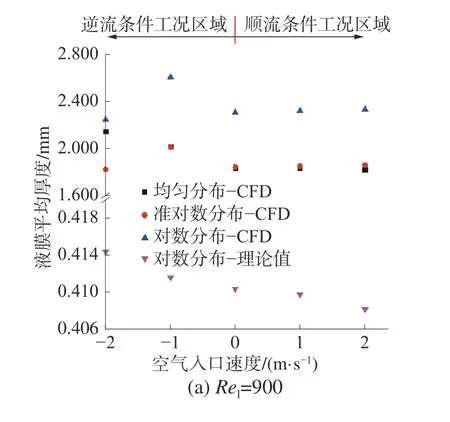
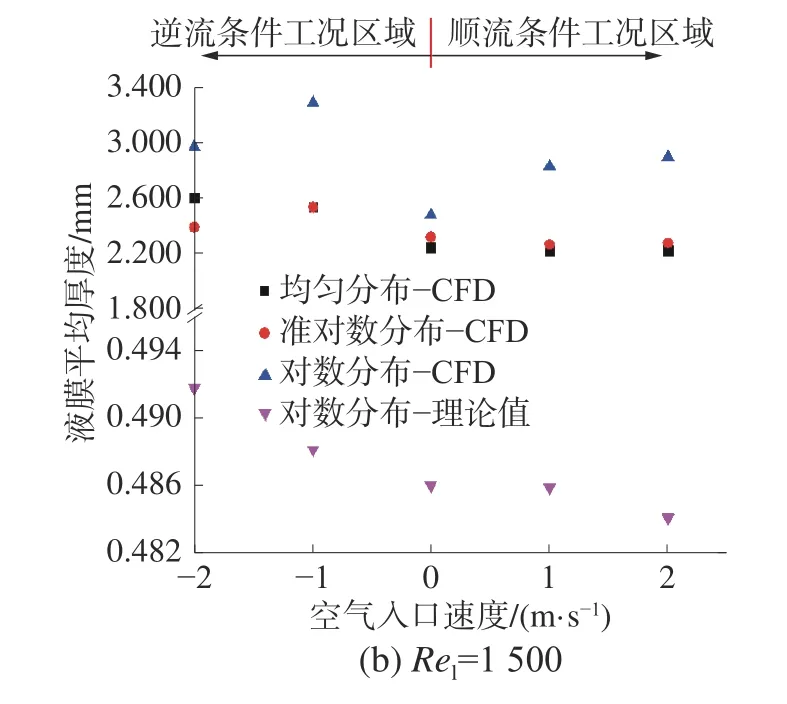
圖9 不同空氣流速條件下平均液膜厚度的變化

主要原因是Nusselt 是基于層流條件而提出的，在大流量下這種平均液膜厚度假設會形成越來越大的偏差[9]。此外，還發現當液膜入口雷諾數和逆向氣流速度較大時，液膜平均厚度在對數分布條件下隨氣流速度的變化也越大，主要原因與氣液界面剪切力的大小和方向相關。

3 結論

本文對二維矩形通道內不同的初邊值條件下降膜流動行為進行了數值研究，主要分析了相應條件下液膜厚度沿流動方向的變化趨勢，得到以下結論：

1）速度分布對液膜厚度沿流動方向的影響主要是通過液膜入口質量流量變化來反映的。對于瞬態流動模擬來說，可用入口準對數速度分布來減少常規均勻分布中流動發展所需的模擬時間。當入口質量流量比較小時，速度分布的影響可以忽略。隨著液膜入口流量增加，準對數分布條件下的液膜波動現象比均勻分布條件下顯著。

2）液膜在較大的入口寬度下呈現出向壁面法向上的堆積，使液膜增厚，所受黏性力增大；而在較小的入口寬度下表現出沿通道長度方向上的鋪展流動，液膜減薄，流速加快，導致液面波動增強。

3）在空氣和水膜并流流動條件下，液膜表面波動現象跟氣液兩相間的速度差有關，兩相間速度差越大，液膜表面波動越劇烈。在液膜入口速度分布為對數分布和準對數分布條件下，氣液波動界面剪切力作用引起液膜入口質量流量的增加對平均液膜厚度的影響較大。

4）氣體流動方向對液膜厚度沿流動方向的變化趨勢影響較大。在并流條件下，重力和界面剪切力合力大于壁面黏性力，導致液膜做加速運動，液膜減薄；而在逆流條件下，壁面黏性力和界面剪切力的合力大于重力，導致液膜做減速運動，液膜增厚。