堰塞壩穩定性快速評估模型
——以小崗劍(上)堰塞壩為例
石振明,程世譽,張清照,薛丹璇
(1.同濟大學 土木工程學院 地下建筑與工程系, 上海 200092;2.同濟大學 巖土及地下工程教育部重點實驗室,上海 200092;3.中國市政工程華北設計研究總院有限公司,天津 300110)
堰塞壩是由火山噴發物、滑坡體、泥石流、冰川堆積物等失穩體橫向阻塞河谷形成的天然壩體。堰塞壩壩體的潰決模式主要有3種:漫頂溢流、管涌、壩坡失穩。堰塞湖蓄水后,上下游產生水頭差,在壩體內形成滲流。當堰塞湖水位低于壩頂時,堰塞壩在滲流力作用下,可發生壩坡失穩和管涌破壞。當堰塞湖水位高于壩頂時,水流沖刷壩體,導致壩體逐漸破壞,即漫頂溢流。堰塞壩可在短時間內發生漫頂潰決[1-2],造成巨大的生命財產損失。1933年四川疊溪和1950年西藏墨脫,均因堰塞壩潰決造成上千人死亡[3]。2008年汶川地震形成257個大小堰塞湖,威脅總人口達130萬人[4]。對不穩定的堰塞壩未及時采取有效的防治手段會對流域內的生命財產安全造成巨大的威脅。而另一方面,對穩定的堰塞壩采取過于保守的處理措施則會造成不必要的資源浪費。
堰塞壩形成初期,有關壩體的工程地質、水文氣象與結構特征等相關資料和信息欠缺,同時受應急治理的時間限制,該階段通常采用經驗方法對堰塞壩的穩定和安全進行快速評估[5],根據歷史上發生的一些堰塞壩案例,選取其中的一些主要控制因素,通過統計擬合分析來預測堰塞壩是否穩定。
在定性分析研究方面,崔鵬等[6]選定壩高、物質組成和堰塞湖的庫容作為判定堰塞湖危險級別的3個指標,并給出危險性分級標準表,建立單個堰塞湖潰決風險評估方法,把堰塞湖潰決風險分為極高危險、高危險、中危險和低危險四個等級,對照分級標準可以快速評定堰塞壩危險等級。堰塞湖風險等級劃分標準[7]根據堰塞湖可能最高水位對應的庫容將堰塞湖的規模簡單劃分為大型、中型、小(1)型和小(2)型,并結合堰塞體物質組成和堰塞體高度將堰塞體危險級別劃分為四個等級。定性分析方法考慮的因素有限,堰塞湖處理條件、匯水面積、水位上漲速度、寬高比、異常滲流、巖基條件等因素未考慮,導致快速評價仍存在不準確性。而且堰塞壩的潰決大多不是一潰到底,如唐家山堰塞壩。以庫容量作為因素之一,使評估結果偏于保守。
在定量分析研究方面,Casagli等[8]提出堆積指數Ib(Blockage Index)和回水指數Ii(Impoundment Index),發現這兩個參數越大,堰塞湖越穩定。其中Ii的規律性較好,統計樣本中的堰塞壩體穩定,則滿足Ii> 0,壩體不穩定,則Ii< 0。Ermini等[9]根據84座堰塞壩資料的統計分析,對堆積體指數法進行修正,利用無量綱堆積指數(DBI)來評估堰塞壩的穩定性。該指數加入壩高這一變量,一方面,壩高影響壩體下游坡度、漫頂時水流速度和沖蝕程度;另一方面,它控制了壩前水位和壩體內水力比降,對壩體的滲流穩定性影響較大。黃來源等[10]利用DBI成功評估了四川什邡青牛沱崩塌群形成的堰塞壩的整體穩定性。但Korup[11]在分析新西蘭的堰塞壩時發現,Ib、Ii和DBI這三個參數并不能很好的區分壩體穩定與否。上述研究表明DBI這種方法的適用具有一定的區域局限性。Hu等[12]采用瑞典條分法計算堰塞壩在不同上下游水位、不同地震荷載等條件下的穩定性,但瑞典條分法不考慮條間作用力,忽略了滲流的影響。年廷凱等[13]根據壩長、壩寬和堰塞湖庫容提出三參數快速評估方法,但選取的參數相對有限。
現有的堰塞壩穩定性評估研究,選取的因素較少,且受區域條件等因素的限制較大。因此,本文從多個評價因素中利用相關性分析選出具有代表性的因素,進行主成分分析建立新變量,提出一種堰塞壩穩定性快速評估模型。實現在較短的時間內,基于易測量、易獲取的相關參數,對堰塞壩的穩定性快速作出定量評價,以便于采取相應應急處理措施,消除堰塞湖潛在風險和隱患,避免產生二次災害。本文以汶川大地震中形成的小崗劍堰塞壩為例,對模型加以應用驗證,進行穩定性分析。
1 小崗劍(上)堰塞壩介紹
四川省綿竹市小崗劍(上)堰塞壩是汶川大地震造成的堰塞壩之一,因清平鄉下游約6 km的綿遠河右岸巖質岸坡發生大規模滑坡阻塞河道形成。小崗劍(上)堰塞壩位于綿竹市綿遠河小崗劍電站上游約300 m處,地理位置為東經104.139 80°,北緯31.493 02°。堰塞湖庫容約1 100萬m3,回水長度4 000 m。堰塞湖河段谷坡高陡,河谷狹窄,為典型的“V”形谷,河道流向整體呈SN向。堰塞體高約70 m~120 m,順河向長約300 m,橫河向長約250 m,總方量約200萬m3。壩頂距滑坡后緣高差約300 m。堰塞體橫河向總體左岸低、右岸高,呈鼓丘狀橫亙在綿遠河上,地形坡度可以分為3段:左側堰體段寬約50 m,地形平緩,坡度2°~5°;中間段堰體寬約120 m,地形坡度18°~20°;右段堰體寬約100 m,地形平緩,坡度0°~5°[14-17]。其主要物質組成為孤、碎塊石,巖性為白云巖、白云質灰巖,巖質堅硬,弱風化為主。堰塞體結構雜亂,架空明顯,原始巖體結構已完全解體。
小崗劍堰塞湖庫容量大,堰塞體較高,且堰塞體單薄,下游地形較陡,大流量、高速度沖刷可能導致堰塞壩局部垮塌,進而導致潰決的可能性極大,對下游漢旺鎮以及綿遠河沿線的城鎮造成巨大威脅。但壩體幾何參數、堰塞湖庫容等多個因素與堰塞壩的穩定性都有緊密聯系,故先通過分析堰塞壩歷史案例各相關參數的情況,確定各影響因素作用下堰塞壩穩定性的計算公式,再利用該判定公式,根據小崗劍(上)堰塞壩的實際參數數值,進行小崗劍(上)堰塞壩的穩定性分析驗證。
2 堰塞壩穩定性評估因素選取
影響堰塞壩穩定性的因素多種多樣,且很多因素并非獨立存在,彼此之間具備相關性。需對各個影響因素作相關性分析,從中選取具有代表性的因素。
2.1 相關性分析
Pearson簡單相關用于衡量兩個數據是否存在線性相關關系,其相關系數計算公式為[18]:
(1)
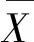
本文選取堰塞壩能快速且定量獲取的穩定性影響因素,包括壩體體積、壩長、壩寬、壩高、回水長度、庫容量。對這些因素進行Pearson相關性分析,從而選取相對獨立的評估因素,得到的結果如表1所示。
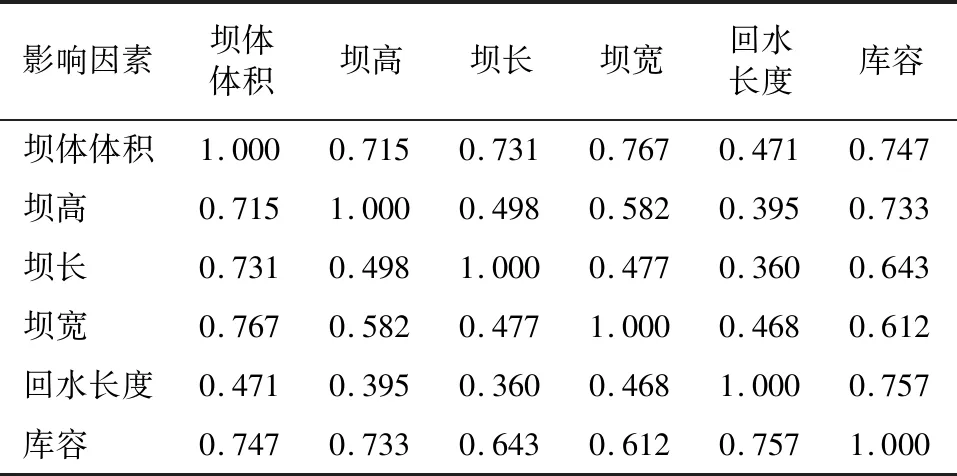
表1 簡單相關系數
表1為各影響因素之間的Pearson簡單相關系數值,數值越大表示兩個變量之間的相關性越強。通過表1可知壩體體積與壩高、壩長、壩寬、庫容相關系數均位于0.7~0.8之間,表明壩體體積與其他四個因素均有強相關關系,應避免壩體體積與壩高、壩長、壩寬、庫容進行組合。故以下穩定性分析不考慮壩體體積,選取其他五個因素進行研究。
2.2 主成分分析
主成分分析是把原來多個變量化為少數幾個綜合指標的一種統計分析方法,通過正交變換將一組可能存在相關性的變量轉換為一組線性不相關的變量。其原理可表述為假定有n個樣本,每個樣本共有p個變量,構成一個n×p階的資料矩陣[19-20]:
(2)
通過變換將原變量指標x1,x2,…,xP轉換為綜合指標z1,z2,…,zm(m≤p)為新變量指標:
(3)
新變量指標z1,z2,…,zm分別稱為原變量指標x1,x2,…,xP的第1,第2,…,第m主成分。每個主成分都能夠反映原始變量的大部分信息,且所含信息互不重復。信息的大小通常用離差平方和或方差來衡量。
本文選取壩長、壩寬、壩高、回水長度、庫容量五個因素進行主成分分析。主成分分析之前先對數據進行KMO和Bartlett 檢驗以確定數據是否適合進行主成分分析。KMO檢驗用于考察變量間的偏相關性,取值在0~1之間。KMO統計量越接近于1,變量間的偏相關性越強,因子分析的效果越好。Bartlett球形檢驗判斷如果相關陣是單位陣,則各變量獨立因子分析法無效[21]。檢驗結果如表2所示。KMO統計量為0.739,說明變量具有相關性;Bartlett球形檢驗卡方值168.641,顯著性P為0.000,達到極顯著水平。兩種檢驗都表明,該數據適合進行主成分分析。

表2 KMO和Bartlett 的檢驗結果
主成分特征值和主成分貢獻率如表3所示。特征值的大小代表了矩陣正交化之后所對應特征向量對于整個矩陣的貢獻程度。選取特征值大于0.5的前三個主成分,第一主成分的特征值為2.887,說明其影響力度較大,第二、第三主成分特征值小于1,說明影響力度相對較小。
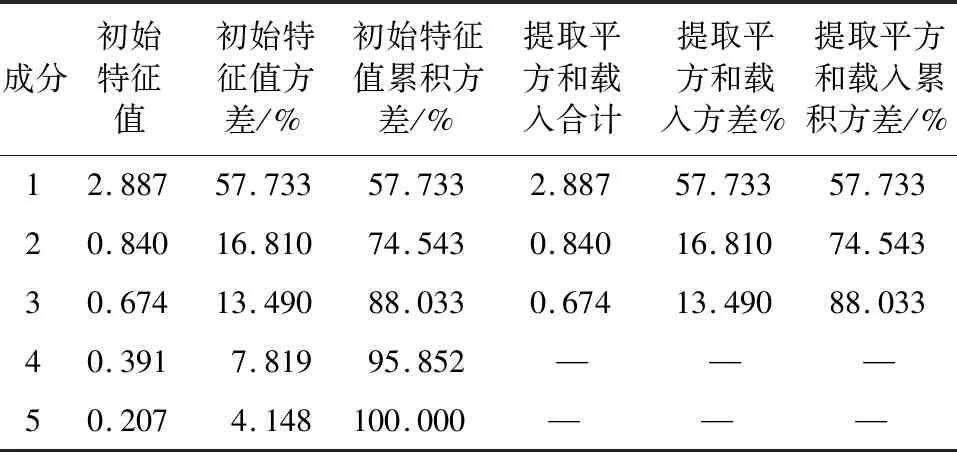
表3 主成分特征值和主成分貢獻率
第一主成分解釋率為57.7%,其重要性遠大于其余主成分,但不能充分包含所有信息,因此,將第二、第三主成分納入分析范圍,共同解釋總方差的88.03%,說明三個主成分綜合原始變量的信息的能力很強。
主成分荷載是主成分分析中原始變量與主成分之間的相關系數。計算各主成分的荷載值得到結果如表4所示。
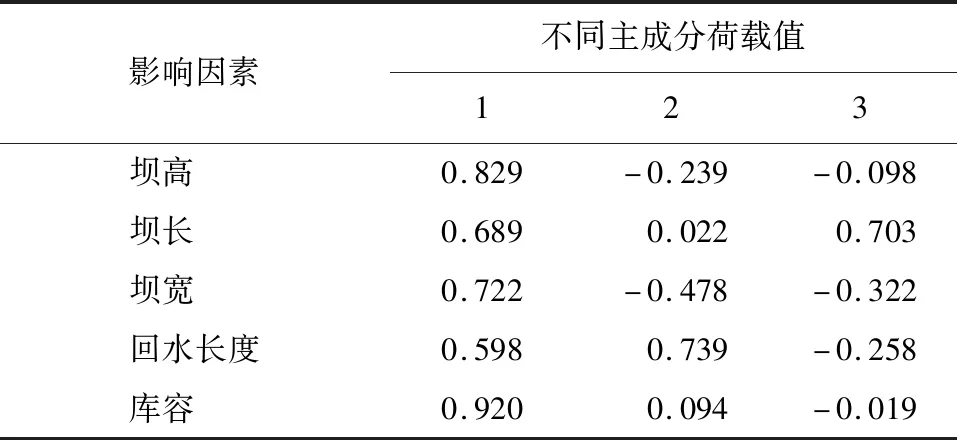
表4 主成分荷載值
表4為三個主成分的荷載值,數值的正負表示影響方向,荷載值的絕對值越大表示變量對主成分影響的強度越大。通過分析表4中荷載值的絕對值可知,在第一主成分中占據主要影響的三個變量是庫容、壩高和壩寬,在第二主成分中占據主要影響的是回水長度和壩寬,在第三主成分中占據主要影響的是壩長和壩寬。由于第一主成分重要性遠大于第二、第三主成分,故壩高、壩寬和庫容的重要性也遠遠大于壩長和回水長度。
3 堰塞壩穩定性評估模型
3.1 邏輯回歸方法
本文采用雙元邏輯回歸模型討論堰塞壩的穩定性,對定性因變量進行回歸分析[22]。
雙元邏輯回歸模型的因變量y是只取0、1兩個值的定性變量,因變量與自變量的關系通常是S型曲線關系。
Z=logit(P)=β0+β1x1+L+βpxp
(4)
式中:P為某種結果的概率;x1、x2…xp為自變量。
以上即為logistic回歸模型。由式(4)可推得:
(5)
P與Z之間的關系如圖1所示。
用雙元邏輯回歸模型討論堰塞壩穩定性,因變量穩定與否用P值表示,其中,P=0代表不穩定,P=1代表穩定,在運算過程中,當0.5 圖1 P-Z函數關系圖 單因素邏輯回歸模型把每個因素單獨作為評估的變量之一。分別建立三變量邏輯回歸模型和五變量邏輯回歸模型,對整理得到的79例堰塞壩案例是否潰決進行判定。 3.2.1 三變量邏輯回歸模型 選取第一主成分的三個因素壩高、壩寬、庫容建立三變量回歸模型,得到模型方程: Z=0.348lnHd+0.254lnWd-0.654lnVl-3.410 (6) 式中:lnHd為取對數后的壩高;lnWd為對數化后的壩寬;lnVl為對數化后的堰塞湖庫容量。利用公式(6)對數據庫中的案例進行穩定性評估并與實際情況對照,模型判斷正確率如表5所示。通過表5可知,三變量回歸模型對不穩定案例的預測結果正確率為91.7%,對穩定案例的預測結果正確率為26.3%,預測結果整體正確率為75.9%。 表5 三變量模型判斷正確率 3.2.2 五變量邏輯回歸模型 三變量邏輯回歸模型準確度不高,不能全面的表征堰塞壩影響穩定性的各個因素,采用全部五變量得到的回歸模型方程為: Z=0.435lnHd+0.076lnLd+0.501lnWd+1.352lnLl-1.122lnVl-15.568 (7) 式中:lnHd為取對數后的壩高;lnLd為對數化后的壩長;lnWd為對數化后的壩寬;lnLl為對數化后的回水長度;lnVl為對數化后的堰塞湖庫容量。 模型判斷正確率如表6所示。由表6數據可知五變量模型對不穩定案例的預測正確率為95.0%,對穩定案例的預測正確率為36.8%,預測結果整體正確率為81.0%,正確率高于三變量邏輯回歸模型。分析原因可能為選取的變量越多,包含的信息越多,可更全面的判斷堰塞壩穩定與否。 表6 五變量模型判斷正確率 單一因素邏輯回歸模型在不穩定堰塞壩的判斷上正確率很高,但在穩定型堰塞壩的判斷上,正確率不足40%。運用此邏輯回歸模型判斷結果過于保守,可能造成處置穩定堰塞壩導致資源的浪費。此外,該評估模型仍存在不穩定堰塞壩判斷為穩定的可能性,可能會影響下游生命財產安全。 為了解決這一問題,考慮到不同影響因素對數化后的值可能不是簡單的線性加減關系,不同變量之間可能存在內在聯系,故采用選取復合因素來進行邏輯回歸分析。 對堰塞壩及堰塞湖的幾何參數進行處理,得到了量綱統一的復合因素,包括壩高因子,高寬比,水流沖擊系數,湖面形狀系數,壩體形狀系數五個定量因素。 采用邏輯回歸法得到的復合因素邏輯回歸模型方程為: (8) 模型判斷正確率如表7所示。 表7 復合因素模型判斷正確率 由表7可知復合因素邏輯回歸模型對不穩定案例預測結果的正確率為98.4%,對穩定案例的預測結果正確率為53.3%,整體正確率為89.9%。與單一因素邏輯回歸變量相比,復合因素模型在穩定堰塞壩、不穩定性堰塞壩及整體正確率上都有提升,尤其是穩定堰塞壩判斷正確率達50% 以上,可以比較準確的判斷堰塞壩穩定與否。 邏輯回歸模型不僅可以預測堰塞壩穩定與否,還可以反映堰塞壩穩定程度。Z值與概率有關,根據概率的不同,可將堰塞壩穩定性劃分為不同的等級。由圖1中S型曲線圖可知,當Z≤-5時,堰塞壩有99%的概率破壞;當Z≥5時,堰塞壩有99% 的概率保持穩定。所以,可根據穩定性系數的不同將堰塞壩穩定性劃分為不同的等級,如表8所示。 表8 堰塞壩等級劃分 邏輯回歸模型對于非穩定堰塞壩的判斷率準確率明顯高于穩定堰塞壩,分析原因可知,實際工程中穩定的堰塞壩案例數明顯少于非穩定堰塞壩,案例數目的差距導致判斷準確性有所差距,本評估模型評估結果偏于保守,但能最大程度的避免將非穩定性堰塞壩判斷為穩定性堰塞壩從而危害下游人民生命財產安全的風險。 將堰塞壩各因素數值代入公式(8),得到堰塞壩穩定性系數Z=-1.54<0,堰塞壩不穩定,會發生潰決。堰塞壩穩定性快速評估模型對不穩定堰塞壩判斷正確率高達98%,故小崗劍(上)堰塞壩判定為不穩定堰塞壩,需采取爆破泄流的應急處置措施,避免對下游造成巨大的生命財產損失。 (1) 采用二元邏輯回歸方法,通過壩高因子、高寬比、水流沖擊系數、湖面形狀系數、壩體形狀系數五個定量因素,建立了堰塞壩穩定性快速評估模型,并具有較高的判定準確率。 (2) 根據堰塞壩穩定性快速評估模型Z值的取值范圍不同,將堰塞壩穩定性進行不同等級的劃分,更加直觀的描述堰塞壩的穩定程度大小,為堰塞壩應急處理的時間和處理措施方式提供有益的參考。 (3) 堰塞壩穩定性快速評估模型是一種定量分析方法,未能考慮堰塞壩物質組成等定性因素,且不能評估堰塞壩成群分布連潰的相互作用,仍有一定的改進空間。但總體來說,堰塞壩穩定性快速評估模型在堰塞壩穩定性評估方面具有積極的實際應用價值,其評價結果可為堰塞壩緊急處置提供一定的理論依據。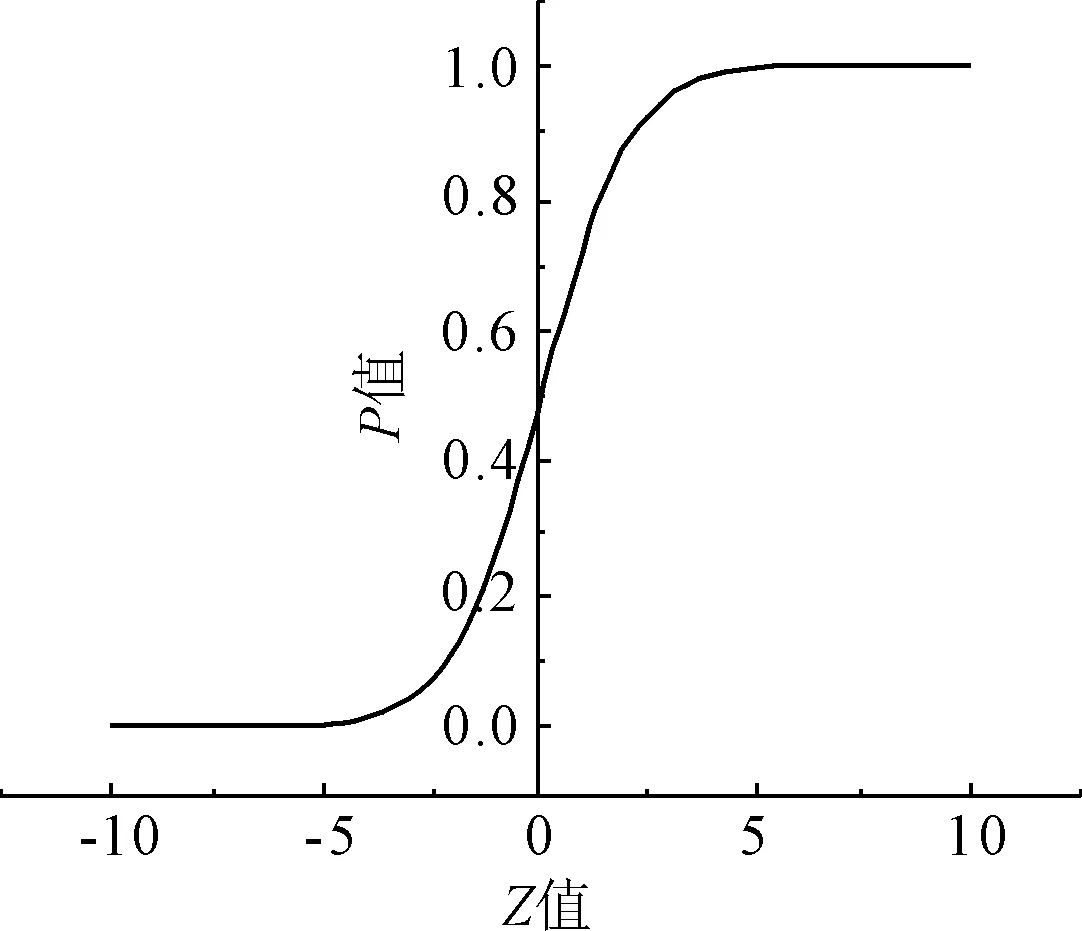
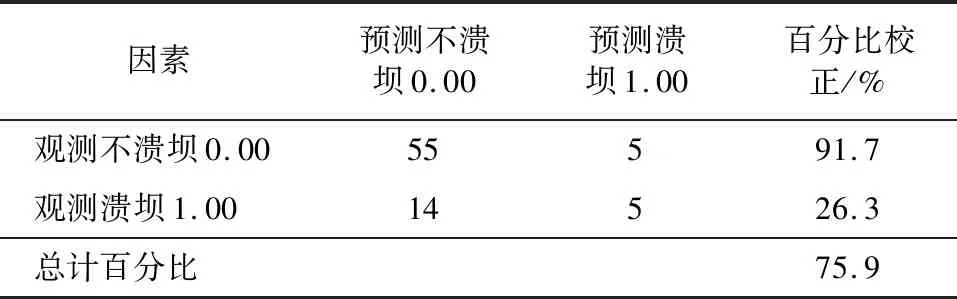
3.2 單因素邏輯回歸模型
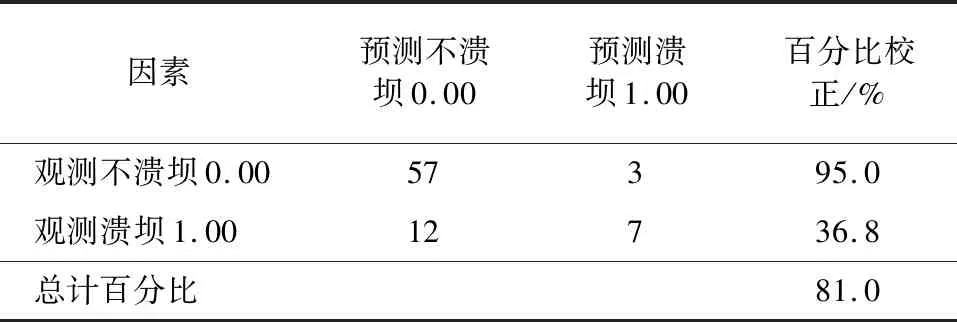
3.3 復合因素邏輯回歸
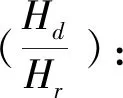
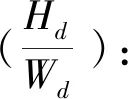
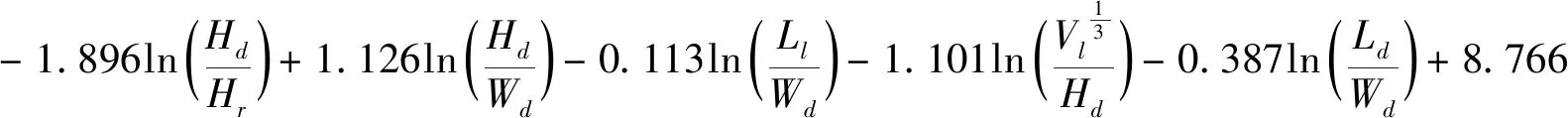


4 結 論

