底部鉸支自復位鋼筋混凝土剪力墻 設計與性能研究

徐龍河，張 焱，肖水晶

(北京交通大學土木建筑工程學院，北京 100044)

鋼筋混凝土剪力墻側向剛度大、承載力高、布置靈活，廣泛用于高層超高層結構中。但當結構遭受較大地震時，易發生墻腳壓潰、墻底出鉸、墻板剪裂等破壞，導致結構殘余變形明顯，無法繼續使用甚至引起建筑倒塌[1]。功能可恢復結構概念[2－3]提出后，國內外學者對剪力墻結構復位方式進行了討論。

Kurama 等[4]基于預應力結構具有變形自恢復特點，首先提出無粘結預應力自復位剪力墻模型，沿墻軸向通長布置預應力筋，放張墻底與基礎連接界面，通過墻體剛性轉動避免墻板損傷，在預應力筋回彈和墻體自重作用下實現剪力墻復位。之后Kurama 等[5]、Holden 等[6]和Marriott 等[7]在預應力自復位剪力墻腳部增設軟鋼棒等耗能裝置以提高墻體耗能能力。黨像梁等[8]提出底部開水平縫自復位剪力墻，墻板與基礎局部放張，僅在墻腳處開水平縫，并在墻內豎向布置通長的預應力筋提供復位力，有效減小開縫導致的墻體承載力下降，復位效果良好。肖水晶等[9－10]提出內置碟簧自復位剪力墻，利用碟簧使用靈活、承載力高、占用空間小等特點設計出可更換型彈性墻腳，代替傳統剪力墻容易破壞的墻腳區域，實現剪力墻側移時墻腳彈性變形并提供恢復力，復位效果良好。趙軍等[11]提出高強筋材混凝土剪力墻，墻內布置鋼絞線或CFRP 筋作為縱筋，通過受力縱筋彈性化的方式減小墻板殘余變形，有效減小墻板破壞區域和裂縫寬度，具有一定的復位能力。目前，剪力墻實現自復位功能的途徑主要有放張墻板與基礎連接界面后布置預應力筋、邊緣約束區底部開水平縫后布置預應力筋、用高剛度高承載力彈性裝置替換易損墻腳和布置高彈性纖維復合筋等幾種方式。

本文從剪力墻塑性鉸區的彈性改造出發，以能實現較大彈性側移為設計目標，將容易受損的鋼筋混凝土墻底替換為能實現彈性轉動的彈性墻底，提出一種底部鉸支自復位鋼筋混凝土剪力墻

(self-centering reinforced concrete shear wall，SC-SW)。基于ABAQUS 有限元軟件對提出的底部鉸支SC-SW 和普通鋼筋混凝土剪力墻(SW)進行模擬，對比了相同受荷歷程下兩者的滯回特性。驗證SC-SW 具有良好復位性能和延性，墻體損傷較低，殘余變形較小，是一種可行的SC-SW 設計方式。

1 SC-SW 力學特性

1.1 SC-SW 設計概念

混凝土彈性變形范圍小，耐壓畏拉，壓應力未達峰值已伴生塑性應變，反復加卸載作用下彈性模量下降明顯。鋼材彈性變形范圍大，屈服強化過程中塑性應變激增。強震作用下鋼筋混凝土發生的塑性應變及混凝土開裂是造成剪力墻殘余變形的主要原因。觀察彎曲型剪力墻破壞模式，墻體多數是由于腳部混凝土壓潰，墻底塑性變形嚴重從而形成塑性鉸，導致殘余位移明顯無法修復，這表明一般鋼筋和混凝土的材料性能難以滿足剪力墻復位功能的實現，因此對受荷過程中應力水平較高的墻底進行彈性改造，不僅可以杜絕墻板絕大部分損傷，還可以賦予剪力墻更優異的性能。本文提出的SC-SW 設計方案如圖1 所示，將型鋼梁與復位支撐組合構造成具有強彈性變形能力的彈性墻底，同時將上部混凝土墻板傳遞的內力解構。由于豎向荷載沿截面分布較均勻，合力作用點偏心小，變形過程中附加彎矩較小，豎向軸力主要由連接梁中部銷軸傳遞，也保證了支撐更換時的豎向承載安全；水平剪力通過中部銷軸傳遞；彎矩通過墻底兩側支撐形成的抗彎力偶傳遞。

圖1 SC-SW 設計方案 Fig.1 Design of SC-SW

高寬比大于2.0 的彎曲型剪力墻具有較好的抗震能力，墻體在軸向壓力和地震水平力作用下，底部截面彎矩最大，墻底混凝土受力最復雜，導致剪力墻在失效過程中大部分損傷集中在墻底，輕則墻腳混凝土壓潰，重則底部裂縫貫通。使用鋼材構造的彎剪分離且具有彈性轉動能力的墻底替換混凝土澆筑的彎剪耦合且塑性明顯的墻底，這種墻底具有材料研究成熟、內力傳遞清晰和性能設計方便的優勢，打破混凝土材料性能約束，適用于高性能剪力墻的設計。

1.2 彈性墻底力學特性

根據本文提出的設計方案，墻腳豎向位移約為1/4 墻頂側移量，而墻腳豎向受力約為2 倍墻頂剪力值。因此，墻底配置的復位支撐要有較大剛度和較強彈性變形能力。本文采用碟簧作為復位支撐的主要受力裝置。為了驗證組合碟簧的受力性能，徐龍河等[12－15]對預壓碟簧自復位耗能支撐進行了循環荷載試驗，表明碟簧具有承載力高、無殘余變形、剛度調整靈活等特點。根據墻體幾何參數和性能需求確定碟簧尺寸及組合方式，以滿足性能目標下的行程需求和剛度需求。將碟簧疊對合兩端加擋板壓縮后限制于內、外管之間，內、外管端部設置與連接梁和基礎梁銷軸連接的耳板。支撐不受外力時，碟簧處于壓縮狀態，對內、外管有一預壓力，當支撐軸力小于等于該預壓力時無法壓縮碟簧，內外管保持靜止，此時支撐剛度由內外管決定(可視為由內管和外管串聯成的鋼管軸向受力變形)。當支撐軸力大于該預壓力時，碟簧開始被進一步壓縮，支撐激活，內外管開始錯動，此時支撐剛度等于碟簧組線剛度。復位支撐構造及原理如圖2 所示。

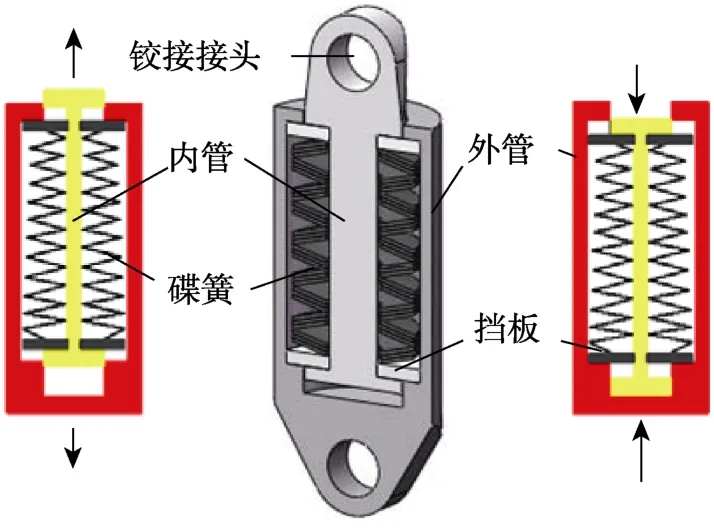
圖2 復位支撐構造及原理 Fig.2 Configuration and principle of self-centering brace

利用ABAQUS 有限元軟件建立復位支撐的實體模型，如圖 3(a)所示。當碟簧組線剛度為20 kN/mm、碟簧預壓力為400 kN、內管抗拉剛度為3.7×105kN/mm 和外管抗拉剛度為1.1×106kN/mm時，支撐在往復荷載作用下滯回曲線如圖3(b)所示，可以看出，支撐初始剛度大，具有雙線性滯回特性；在第一、第二剛度范圍內，均能實現大位移彈性變形，驗證了上述支撐彈性機制的有效性；內管、外管和擋板的變形對支撐剛度有一定的影響，例如支撐受拉時，墊板翹曲、內管拉伸和外管拉伸三種變形可以造成支撐第一剛度與第二剛度間的曲型過渡段，而支撐受壓時內外管因僅端部受力，變形不明顯而不會造成曲線過度段；由于內外管、碟簧組和擋板串聯關系的影響，支撐第二剛度會略小于碟簧組線剛度。增大內外管和擋板的剛度會有效減小這三者變形產生的影響，因此應合理控制這三者的剛度。同時，由于支撐具有穩定簡單的力學特性，不考慮內外管和墊板變形產生的影響時，為提高計算效率，可用雙線性彈簧對復位支撐軸向力學性能進行簡化模擬。

剪力墻彎剪作用下，墻板混凝土應力水平從兩側墻腳向截面中部和墻板上部遞減，因此墻體在彎曲破壞時墻底塑性區域呈現兩邊高中間低的分布形狀，墻底分布的裂縫也向墻板中部傾斜。為簡單有效地替換墻板塑性破壞區，選取V 型界面以下為替換區，用V 型連接梁與上部鋼筋混凝土墻板銜接，承受和傳遞墻體內力。V 型連接界面不僅符合墻板受力特點，而且擁有較大的粘結面，墻內軸壓對粘結面剪力傳遞有增強作用，可使墻底與上部墻板整體性更高。

圖3 復位支撐有限元模型與滯回曲線 Fig.3 Finite element model and hysteresis curve of self-centering brace

1.3 SC-SW 工作原理及理論骨架曲線

圖4 給出了SC-SW 理論骨架曲線。SC-SW 骨架曲線具有雙線性特性，在剛度轉變處，支撐發生激活，彈性墻底進入第二剛度階段，導致SC-SW側向剛度下降，該力學行為與傳統剪力墻屈服相似，但此時SC-SW 各部件仍處于彈性狀態，稱SC-SW 因支撐激活剛度開始下降點為類屈服點。

通過調節彈性墻底兩側支撐第一剛度可調整墻底截面初始轉動剛度，可實現替換區域的轉動剛度與傳統剪力墻相等，使得SC-SW 初始剛度與原墻相等；墻體激活位移由復位支撐設計參數與墻底幾何尺寸決定，可依據性能要求確定SC-SW 激活位移大小，做到側移達到原墻屈服位移時激活；SC-SW 墻底進入第二剛度階段后墻底轉動位移增大的同時內力增長緩慢，上部墻板內力不會激增，仍處于彈性階段，該過程與傳統剪力墻屈服后力學行為相似，通過調節復位支撐第二剛度可對SC-SW激活后剛度和承載力進行設計，做到與原墻承載力相等；由于彈性墻底受力機制清晰，內力解構準確，調節復位支撐有效行程可對墻底轉動行程進行設定，從而可對SC-SW 進行延性設計。

剪力墻是高層結構核心受力構件，應盡量不發生損傷。本文提出的SC-SW 旨在實現墻體目標位移下的彈性變形，不以墻體發生塑性變形甚至破壞為代價換取能量消耗能力，墻體在荷載消失后可在彈性墻底的恢復力矩作用下復位，不產生殘余位移。

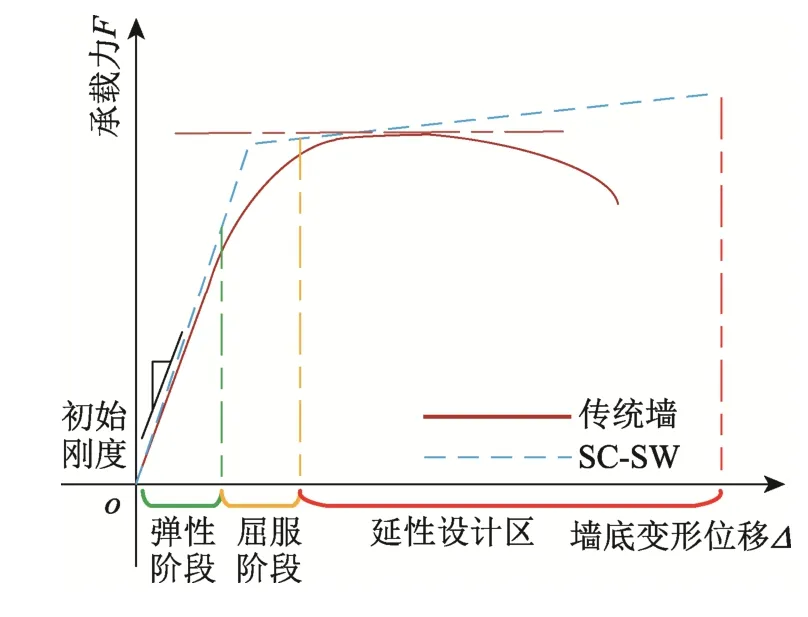
圖4 SC-SW 理論骨架曲線 Fig.4 Theoretical skeleton curve of SC-SW

2 SC-SW 滯回性能模擬

2.1 建模方法

在ABAQUS 軟件中建立普通SW 和底部鉸支SC-SW 的有限元模型，幾何尺寸如圖5 所示，配筋和材料參數均見參考文獻[16－17]。試件SW 軸向受荷為1821 kN，屈服后采用位移控制加載，按位移角為1/275、1/100、1/75 逐級加載，每級加載循環2 次。

混凝土單軸拉壓應力-應變曲線采用《混凝土結構設計規范》(GB50010－2010)中建議的曲線，邊緣約束區混凝土采用錢稼茹曲線[18]，本構采用塑性損傷模型，塑性損傷因子采用文獻[19]中介紹的方法計算。鋼筋采用方自虎等[20]開發的適用于模擬鋼筋混凝土結構滯回行為的本構模型及材料子程序進行模擬。連接梁與基礎梁鉸接，采用理想彈性模型進行模擬。

模型中材料屬性依據試驗實測值確定。鋼材性能較優、加工性好，鋼部件容易進行彈性設計，因此本文模型中不考慮鋼梁和鉸接接頭屈服。

圖5 SC-SW 與SW 構造圖 Fig.5 Configuration of SC-SW and SW

2.2 SW 模型驗證

試件SW 的破壞形態和裂縫分布如圖6 所示。加載過程中，荷載達到一定值時墻板與基礎連接界面出現水平裂縫，最外層豎向鋼筋繼而屈服；隨著荷載增大，墻板形成新的水平裂縫并延伸擴展；當荷載達到峰值時，墻腳混凝土壓潰剝落，試件承載力開始下降；位移繼續增加，墻底混凝土塑性破壞區向中部蔓延，墻體下墩，喪失承載力，最終呈彎曲型破壞形態。

SW 有限元模型如圖7(a)所示，與試驗滯回曲線[16]對比如圖8 所示。模擬所得墻體屈服荷載、峰值荷載和破壞荷載在正向加卸載過程中誤差分別為4.26 %、3.60 %和9.23 %，在反向加卸載過程中分別為2.94 %、4.00 %和1.00 %，誤差較小。正向加卸載與反向加卸載過程中最大殘余位移誤差分別為4.8 mm 和2.11 mm。當荷載位移較大時試件墻腳混凝土損傷嚴重，鋼筋與混凝土滑移明顯，在試件正向卸載向反向加載交替過程中墻體腳部鋼筋由受拉卸載至受壓發生屈曲，滯回曲線表現為明顯捏縮，而有限元模型對該效應模擬能力有限，引起殘余位移存在誤差。總體而言，有限元模型與試驗實測曲線吻合良好。因此，本文所述建模方法可有效模擬試驗試件的力學性能。

圖6 SW 破壞形態與裂縫分布 Fig.6 Failure form and crack distribution of SW

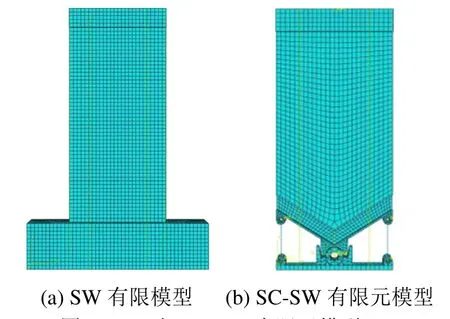
圖7 SW 與SC-SW 有限元模型 Fig.7 Finite element models of SW and SC-SW

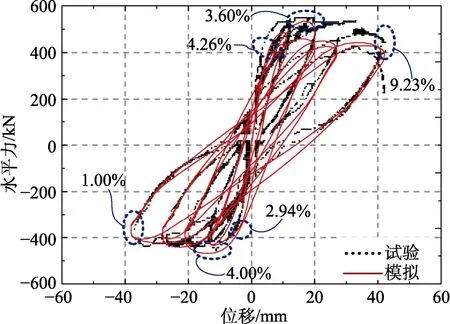
圖8 SW 模擬與試驗滯回曲線對比 Fig.8 Comparison of hysteresis curves between simulation and experiment of SW

2.3 SC-SW 模型

以等初始剛度和等承載力準則對SC-SW 進行設計。為了將SW 中墻底塑性破壞區域進行有效替換，根據剪力墻塑性鉸高度統計經驗，SC-SW 中墻底替換區外側高度h1取600 mm；根據連接梁與基礎梁銷軸連接構造需求，SC-SW 墻底替換區中間高度h2取200 mm；替換區域厚度t與墻板相同，取160 mm。

采用一維等截面懸臂梁模型對SC-SW 與SW進行對比分析。假設SC-SW 與SW 截面特性相同，則相同荷載作用時候，距基礎h1高度處二者截面轉角相同，根據SC-SW 與SW 初始剛度相等，由SW初始剛度K0、墻板高度H、截面抗彎剛度EI和截面高度hw確定SC-SW 墻底兩側支撐第一剛度K1：

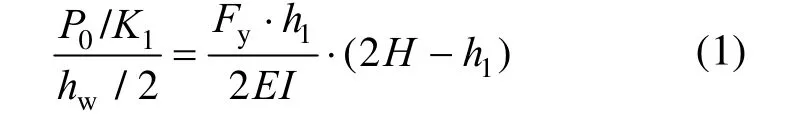
整理得：

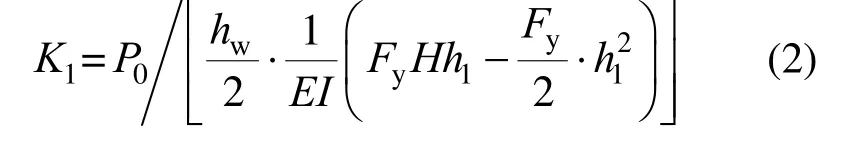
假設SC-SW 在屈服荷載作用下支撐激活，限制SC-SW 類屈服時水平荷載介于SW 屈服荷載與峰值荷載之間(此處選取二者均值)，由SW 屈服荷載Fy與峰值荷載Fp確定支撐碟簧預壓力P0，力矩平衡方程有：

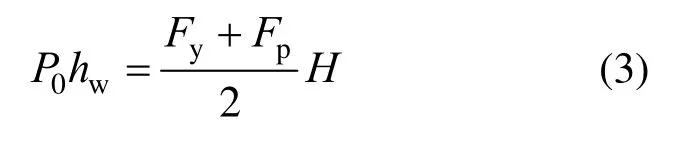
整理得，

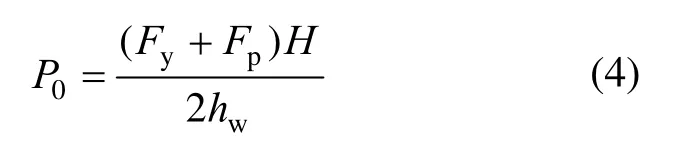
由于SC-SW 支撐激活后內力增長幅度小，假設上部墻板僅發生剛體轉動，根據SC-SW 極限位移不小于SW，承載力不小于SW，由SW 峰值荷載Fp和極限位移δu確定支撐第二剛度K2(此處以SC-SW 位移達到δu前最大承載力不低于Fp為條件)，當墻體頂部發生側移Δ時，有：

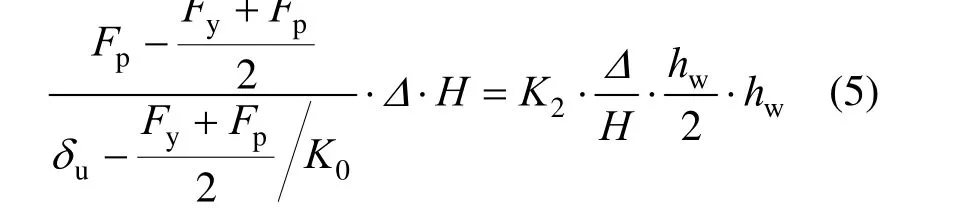
整理得：

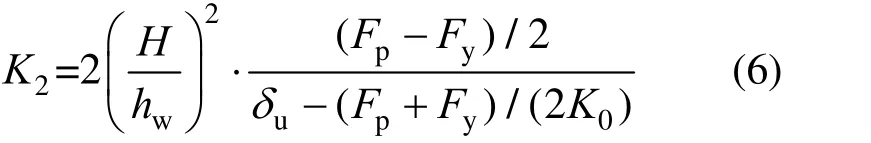
SC-SW 有限元模型如圖7(b)所示。墻體幾何尺寸參考圖5，截面配筋和材料參數設置與SW 一致，連接梁與基礎梁僅考慮彈性變形。由于墻底兩側支撐的力學特性簡單穩定，通過軸向連接器進行等效模擬，并通過K1、P0和K2值對連接器軸向力與位移關系進行設定。

3 SC-SW 性能對比分析

3.1 滯回性能對比

根據SW 力學性能對SC-SW 進行等效設計，由式(2)、式(4)和式(6)計算K1、P0和K2為1850 kN/mm、925 kN 和24 kN/mm，二者滯回曲線對比如圖9 所示。可以看出，SC-SW 滯回曲線具有雙線性特性，支撐激活前剛度下降不顯著。不同加載幅值下滯回曲線基本重合，包絡面積較小，表明墻體損傷程度低。卸載時殘余位移較小，復位性能較好。

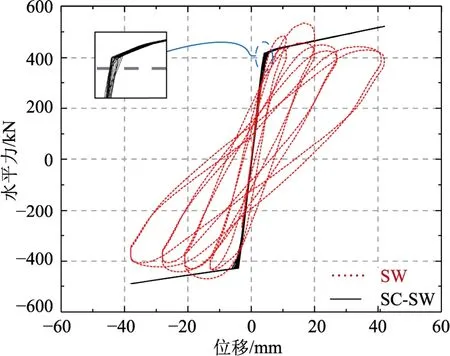
圖9 SC-SW 與SW 滯回曲線對比 Fig.9 Comparison of hysteresis curve between SC-SW and SW

SC-SW 與SW 承載能力對比如表1 所示。其中，由等效彈塑性屈服法求得SW 屈服荷載，對應位移為屈服位移。定義SC-SW 由于支撐激活剛度發生轉變的點為類屈服點，對應的水平荷載和位移為類屈服荷載和類屈服位移，并與SW 的屈服荷載和屈服位移進行對比。定義SW 峰值荷載的85 %為極限荷載，對應位移為極限位移。由于SC-SW 在受荷過程中未發生剛度下降，定義受荷過程中所受最大荷載為峰值荷載，對應位移為峰值位移，位移角達塑性限制0.02 時的位移為極限位移，對應荷載為極限荷載。可以看出，SC-SW 的類屈服荷載和類屈服位移與SW 相近，二者初始剛度分別為90 kN/mm和86 kN/mm。二者峰值荷載相近，但是SC-SW 在剛度轉變后呈現強化特性，沒有出現下降段，峰值荷載與極限荷載出現在最大加載位移處。總體來看，SC-SW 滯回曲線與SW 骨架線相近，實現了屈服荷載、峰值荷載和屈服位移的等效設計。定義極限位移與屈服位移的比值為延性系數，用于衡量剪力墻的延性。SC-SW 與SW 延性系數分別為8.92和7.05，提高了26.52 %，表明SC-SW 具有更好的變形能力。

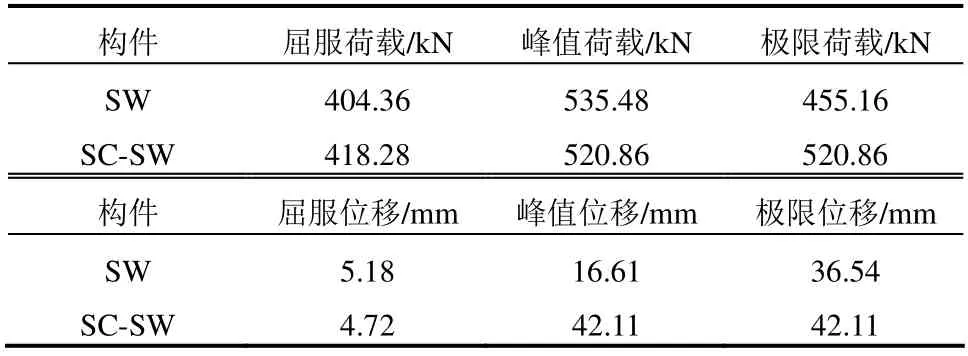
表1 SC-SW 與SW 力學特征對比 Table 1 Comparison of mechanical characteristics between SC-SW and SW

3.2 耗能能力與復位能力對比

不同幅值位移加載過程中SC-SW 與SW 累計耗能對比如圖10 所示。從圖可以看出，二者累計耗能均隨著加載幅值的增加而增加，但SW 累計耗能增加顯著，SC-SW 增加緩慢。加載幅值較小時，二者均處于彈性階段，墻體無損傷，耗能少。隨著加載幅值增大，SW 屈服發生塑性變形，墻板裂縫擴展，墻底混凝土進入塑性破壞階段，墻體損傷逐漸增大，混凝土的塑性變形和鋼筋的屈服耗散大量能量。SC-SW 在側移增加過程中墻底兩側支撐軸力超過碟簧預壓力，支撐激活，墻體剛度轉變，進入第二剛度階段。SC-SW 剛度轉變時上部墻板混凝土應力應變水平低，未進入塑性破壞階段，而剛度轉變后由于墻底轉動，水平荷載增加緩慢，墻體內力不會激增，混凝土大部分仍會處于彈性階段。SC-SW在發生較大側移時，上部混凝土和下部墻底主要發生彈性變形，塑性變形和損傷較少，因此幾乎不耗散能量。同時表明需要在整體結構中增設耗能裝置來耗散因SC-SW 不能發生塑性變形而無法耗散的能量。

SC-SW 與SW 殘余位移對比如表2 所示。可以看出，SW 殘余位移隨加載幅值增加而增大，最大殘余位移角達0.58 %，殘余變形明顯，混凝土破損后修復困難，導致構件喪失完整性無法繼續使用。SC-SW 殘余位移不超過2 mm，殘余位移在加載幅值遞增過程中增加緩慢，驗證了本文提出的設計方案可實現剪力墻大側移下的低損傷彈性變形，具有較好的復位能力。

3.3 損傷分布對比

SC-SW與SW在第一次達到峰值荷載和末次循環加載極限荷載作用下混凝土墻板受壓損傷(DAMAGEC)分布如圖11 所示。

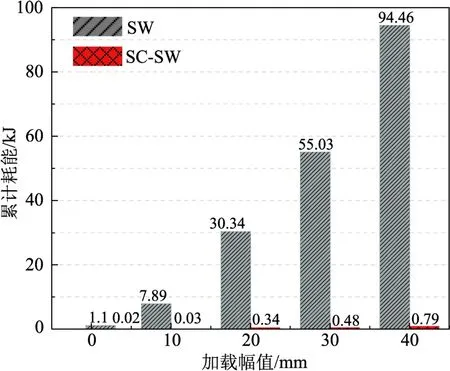
圖10 SC-SW 與SW 累計耗能對比 Fig.10 Comparison of accumulative hysteretic energy dissipation between SC-SW and SW

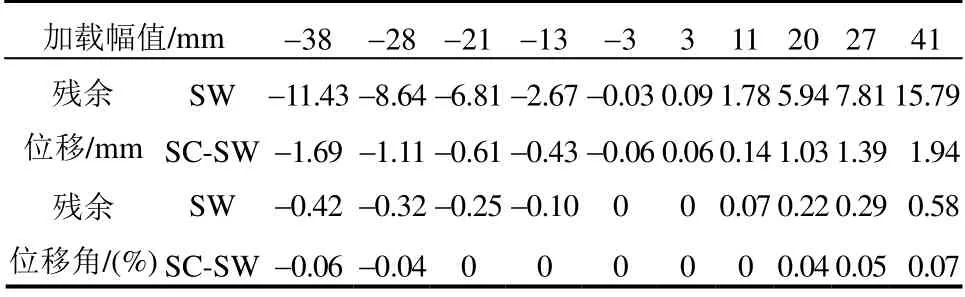
表2 SC-SW 與SW 殘余位移對比 Table 2 Comparison of residual deformations between SC-SW and SW

圖11 SW 與SC-SW 受壓損傷分布 Fig.11 Concrete compression damages of SW and SC-SW

可以看出，SW 受壓損傷主要發生在墻底且集中在兩側墻腳，這與試驗所記錄到的試件破壞現象與彎曲破壞模式一致。峰值荷載作用下，SW 墻腳已經形成一定程度的損傷，而SC-SW 混凝土部分基本沒有損傷。極限荷載作用下SW 損傷程度加重，由于反復加卸載，墻腳損傷逐步積累，損傷較大區域與試件試驗破壞時底部混凝土壓潰剝落區域一致，墻底受損嚴重，兩側墻腳破壞。而SC-SW 僅在連接梁兩端處發生混凝土的輕度損傷。從受壓損傷對比可以看出，本文提出的SC-SW 有效地將SW受荷過程中受壓損傷嚴重的區域進行了替換，在水平荷載移除后，SC-SW 由于在上次荷載激勵過程中未形成明顯受壓損傷，混凝土性能保持在健康水平，剪力墻整體功能完整，實現了功能恢復的目的。

SC-SW與SW在第一次達到峰值荷載和末次循環加載極限荷載作用下混凝土墻板受拉損傷(DAMAGET)分布如圖12 所示。

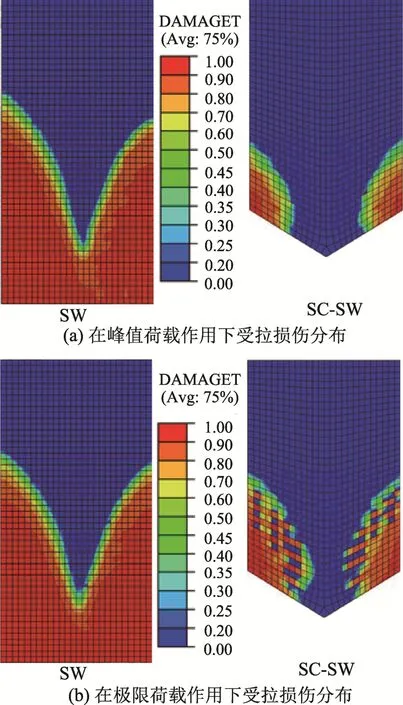
圖12 SW 與SC-SW 受拉損傷分布 Fig.12 Concrete tensile damages of SW and SC-SW

可以看出，SW 在經歷屈服至極限荷載作用過程中受拉損傷發展不明顯，幾乎在屈服荷載作用時已達到最高水平，而受拉損傷程度高的區域與試件試驗過程中墻板開裂區域一致。由于混凝土是與墻內豎向鋼筋共同澆筑，在水平荷載不高時，混凝土與鋼筋共同承擔墻板拉力，鋼筋拉伸，混凝土應力超過受拉極限發生開裂，即使水平荷載遞增，受拉裂縫早已形成。而SC-SW 在峰值荷載作用下混凝土受拉損傷程度較輕，加載至極限荷載過程中損傷會逐步發展，損傷區域從連接梁兩側向墻板中部和上部擴展，最終損傷程度比SW 小。因為連接梁可以整體轉動，變形過程中對上部墻板有承托作用，梁體自身變形較小，比起SW 同等位置混凝土對上部墻板的作用力，連接梁更均勻，使得上部混凝土受力更均勻，受拉損傷程度降低。

通過受拉損傷和受壓損傷對比可以看出，SC-SW 主要減輕的是墻板混凝土受壓損傷，對混凝土受拉損傷有一定程度的控制，但還是有一定程度的發展。對于受彎型鋼筋混凝土構件，損傷和破壞主要因混凝土受壓造成，針對受壓損傷進行改善對構件損傷控制效率更高。

4 結論

本文提出一種底部鉸支自復位鋼筋混凝土剪力墻，并對其構造和工作原理進行了介紹。通過數值模擬對新型自復位墻與普通鋼筋混凝土剪力墻的力學性能進行了對比分析，得到以下結論：

(1) 采用碟簧構造的復位支撐與型鋼梁組合成彎剪解耦的彈性墻底，對傳統剪力墻失效時塑性破壞嚴重的墻底進行替換后，能實現剪力墻較大側移彈性變形，殘余位移顯著降低，復位性能較好。同時可承擔較大豎向荷載并提供較大側向剛度。

(2) 復位支撐具有雙線性滯回特性，可使SC-SW 也具有雙線性滯回特性。通過對復位支撐的參數調整，可實現SC-SW 與傳統墻等初始剛度和等承載力設計。與相同截面傳統剪力墻相比，SC-SW 的延性提高了26.52 %，延性設計方便可行。

(3) SC-SW 在變形過程中損傷小破壞輕，通過混凝土開裂和塑性變形方式耗散的能量少，剪力墻性能可在多次激勵后保持在健康水平。

(4) SC-SW 有效的減輕了混凝土墻板受壓損傷，使剪力墻整體在經歷較大變形后仍處于彈性狀態。對受拉損傷的發展有遲滯作用，損傷程度得到一定程度的控制。