密集橫隔板UHPC箱梁錨固區局部效應分析及配筋設計

李傳習，馮 崢，郭立成，柯紅軍，劉科強

(1.長沙理工大學 橋梁工程安全控制教育部重點實驗室，湖南 長沙 410004；2.佛山市路橋建設有限公司，廣東 佛山 528303)

0 引言

后張預應力混凝土梁橋的錨固區受到預應力集中錨固張拉力的作用、鋼束局部彎曲引起的徑向力作用，存在局部承壓和應力擴散等問題，被認為是混凝土結構中的典型應力擾動區(D區)[1]。錨固區的局部承壓強度及抗裂性能會影響到整個橋梁結構的安全性、耐久性。文獻[1-4]利用有限元及拉壓桿模型對普通混凝土箱梁錨固區進行了系統的受力分析研究，相關研究成果被采納于《公路鋼筋混凝土及預應力混凝土橋涵設計規范》(JTG 3362—2018)[5](后文簡稱為JTG—2018)中。普通混凝土箱梁錨固區在受力分析及配筋設計上已較為明確。但由于普通混凝土材料強度較低，預應力錨固區開裂現象較為普遍。且現有已建大跨度預應力混凝土梁橋在運營過程中普遍出現了主跨過度下撓和梁體開裂的問題[6]，而采用高性能水泥基材料被認為是解決此類問題的最有效方式，也是橋梁建設未來的發展方向。

隨著超高性能混凝土(UHPC[7-9])的快速發展，UHPC已被廣泛用于橋梁結構中[10-11]。文獻[12-13]提出了密集橫隔板UHPC連續箱梁橋的概念，該橋型使得橋梁上部結構的自重可減輕約50%，具有良好的綜合經濟性。采用UHPC建造大跨度橋梁的理念正逐漸深入人心[6]。相應地，UHPC橋梁中預應力錨固區的局壓性能成為了人們關注的重點。雖可以參考普通混凝土局壓區的設計經驗，但UHPC從微觀結構到宏觀力學性能與普通混凝土相比均有較大差異，其內部微裂紋發展、外部開裂直至破壞的整個非線性過程也有其自身特點。并且由于UHPC薄壁箱梁橋頂板、腹板和底板厚度均較薄，預應力鋼束需要采用體外束，大量的體外預應力束通過尺寸較小的轉向塊或齒塊錨固在壁板上。因此，過于薄壁化的結構將會導致預應力UHPC箱梁橋錨固塊、錨固處的頂底板和錨固隔板成為關鍵的受力部位，而國內外相關的技術研究還不夠充分。

文獻[14]對UHPC連續箱梁錨固區進行了線彈性有限元分析，研究了錨固區的4種典型局部效應，并得到了壁板厚度對錨固區局部彎曲效應的影響規律，且經計算發現了將齒塊錨固于相鄰橫隔板之間具有最優的錨固效果，但未對該錨固方式下錨固區的局部效應開展更深入的參數研究，例如未關注錨固處隔板寬度、隔板間距及多齒塊錨固作用對錨固區受力性能的影響，尚需進一步的研究。

拉壓桿模型法是解決錨固區應力復雜問題的一種有效方法，因而確定拉壓桿模型的幾何構形是進行隔板連通式齒塊(齒塊置于橫隔板與橫肋之間或相鄰橫隔板之間)配筋設計的重要手段。但因隔板的存在，隔板連通式齒塊錨固區的應力分布特征和力流傳遞規律與傳統齒塊錨固區[2-4](包括獨立矩形齒塊、獨立三角齒塊、角隅矩形齒塊等)明顯不同。理解這一應力分布特征所抽象的幾種典型局部作用效應及相應的拉壓桿模型應有所區別，但目前針對此方面的研究還較為缺乏。

本研究以某擬建UHPC連續箱梁橋為工程背景，利用ABAQUS對隔板連通式齒塊的局部作用效應進行了多種參數研究，分析了隔板設置情況、隔板寬度、隔板間間距以及多齒塊錨固對隔板連通式齒塊受力性能的影響，并在此基礎上提出了隔板連通式齒塊錨固區拉壓桿模型的構建方法，且給出了配筋設計實例。

1 工程背景與簡化的分析對象

以某擬建UHPC連續梁橋為基本原型進行錨固區的局部效應分析。該橋為三跨(56+103+56) m變截面UHPC連續箱梁橋，梁寬16.75 m，頂板處采用帶肋板，肋板最厚處為25 cm。橫隔板板厚12 cm，橫隔板間距為3 m。在相鄰橫隔板的中間部位設置橫肋，肋板厚為20 cm，肋板高度為60 cm。箱梁腹板厚度為18～25 cm。頂板束齒塊錨固端面高47 cm，寬40 cm。鋼絞線為19束布置，均采用直徑為15.2 mm、標準強度為1 860 MPa的普通無黏結成品索，波紋管的孔徑為12 cm。普通鋼筋采用HRB400級鋼筋。箱梁鋼束錨固示意參見圖1。

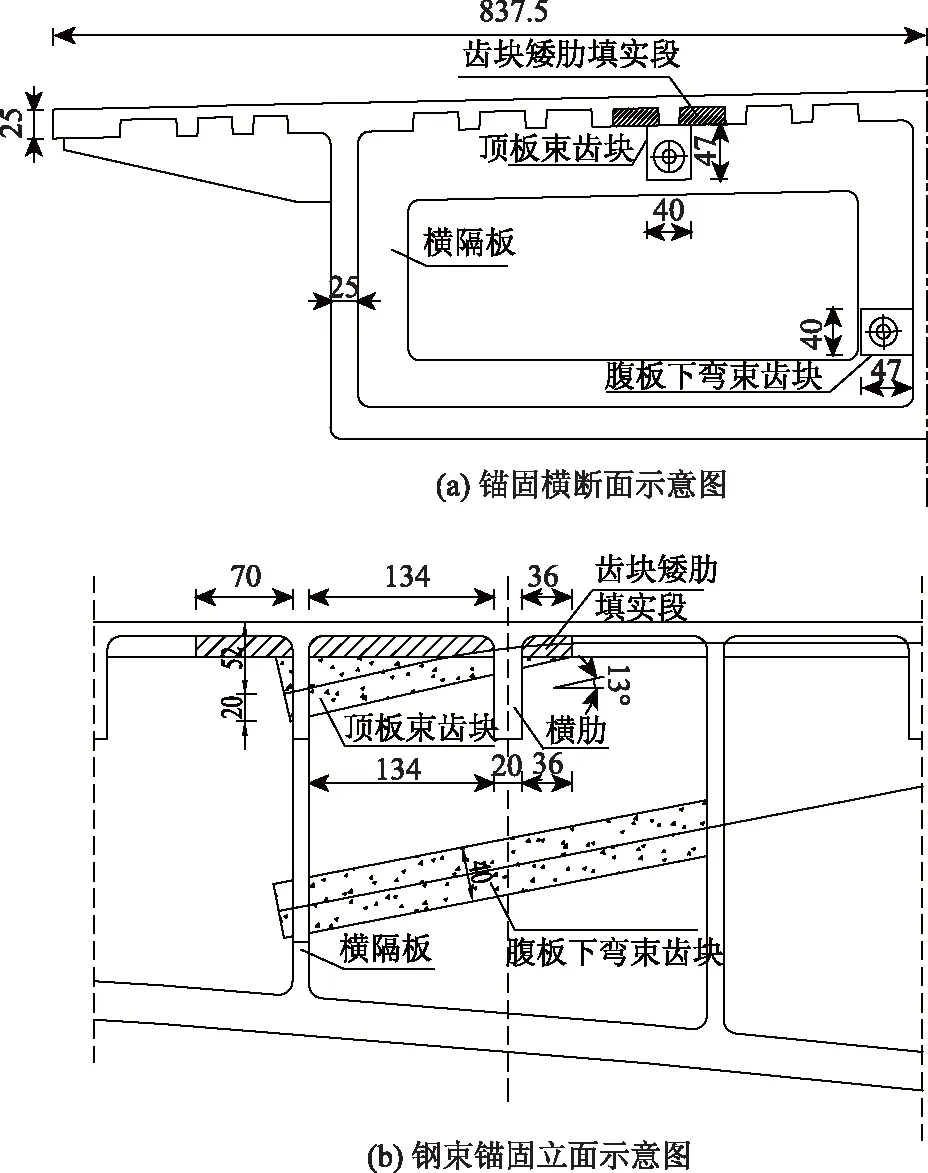
圖1 箱梁鋼束錨固體系示意圖(單位：cm)Fig.1 Schematic diagram of steel stand anchoring system for box girder (unit: cm)

為獲得隔板連通式齒塊錨固區的應力分布特征以及隔板等參數變化下的主應力變化情況，僅取出背景工程中頂板三角齒塊錨固區的基本尺寸進行研究，而箱梁橋錨固區真實的受力情況另文研究。基于此，為便于參數分析，在箱梁原設計的基礎上保持錨固區的基本尺寸不變對結構進行簡化，簡化的分析模型詳細設計尺寸如圖2所示。該模型頂板部位簡化為平板，頂板和底板的厚度分別為220 mm和180 mm；腹板厚度取最小值180 mm；模型高度為2.5 m，長度為4S(S為橫隔板與橫肋之間的距離，無特別說明時取1.5 m)，模型寬度為(L+360) mm(L為相鄰腹板內側面間的距離，即橫隔板寬度)；錨固齒塊設置在簡化模型的正中間(有特別說明時除外)；齒塊、橫隔板和橫肋尺寸與原設計一致；預應力仍按19束鋼絞線設計，計算時荷載按70%的標準強度取值。

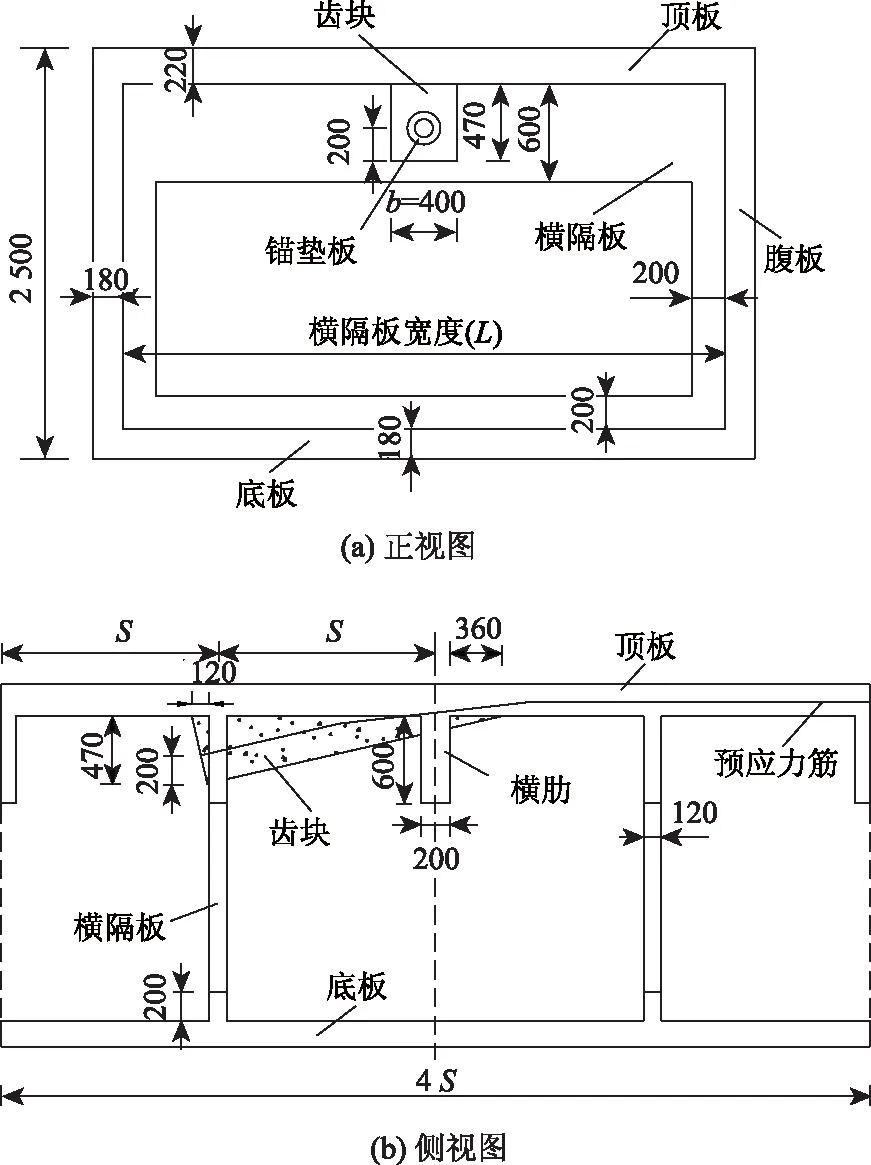
圖2 簡化的分析模型設計尺寸(單位：mm)Fig.2 Dimensional design of simplified analytical model (unit: mm)

利用ABAQUS對簡化的分析模型錨固區進行線彈性分析，UHPC箱梁采用八節點六面體縮減積分單元C3D8R模擬，UHPC材料參數按該橋擬采用的UHPC材性試驗結果取值，彈性模量E取44.0 GPa，泊松比υ取0.2。根據文獻[15]的研究成果，有限元模型考慮了預應力孔道對錨固區受力性能的削弱作用。為對后續拉壓桿模型的構建提供有利的參考，模型未考慮普通鋼筋及錨墊板等對錨固區受力性能的影響。錨固張拉力等效簡化為均布荷載施加于錨板上，作用范圍與錨墊板的受力面積保持一致，鋼束轉向產生的徑向力亦采用均布力施加于轉向位置處。邊界條件設置為約束梁段兩端X，Y，Z，這3個方向上的自由度。對模型錨固區合理密布網格，關注部位網格細化至10 mm，保證各部位的計算結果收斂良好。本研究的各有限元模型均基于該方法建立，由于有限元模型數較多，故后續不再贅述。

2 應力分布特征

2.1 拉應力分布特征

根據有限元結果可知，隔板連通式齒塊與常規獨立三角齒塊在受力效應上大體相同，但由于錨固隔板的受力介入，隔板連通式齒塊受力要更為復雜。去除拉應力量值較小的部分，將錨固區拉應力的集中分布特征歸因于6種典型局部效應，參見圖3。除常規獨立三角齒塊中的錨下劈裂效應、錨后牽拉效應、局部彎曲效應、徑向力效應、懸臂效應外[4-5]，還包括橫隔板部位的隔板彎曲效應。

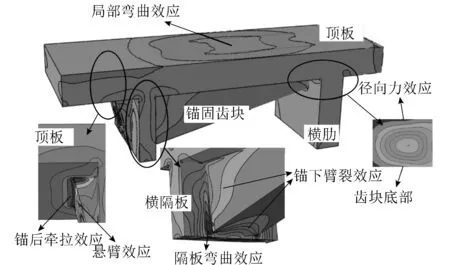
圖3 隔板連通式齒塊典型局部效應Fig.3 Typical local effect of DABIAS

前5種局部效應文獻[4]及規范[5]針對常規獨立三角齒塊已做了詳細的論述，此處不再細述。而隔板連通式齒塊特有的隔板彎曲效應主要體現在橫隔板內側面與齒塊交接區域的橫向拉應力以及豎向拉應力值較大，存在較為明顯的應力集中現象。這是由于錨固處橫隔板在周邊壁板的約束下形成一個三邊固結一邊自由的受力板，在齒塊預應力的作用下產生了局部彎曲，使得該部位面外應力較為顯著。

2.2 壓應力分布特征

圖4為錨固區的壓應力等值線圖，從圖中可以看出錨固區中齒塊體的壓應力值較大。橫隔板與橫肋之間的齒塊部位存在核心受壓區，即壓應力沿縱橋向先增大后減小，并呈拱狀分布，位于距離橫隔板中心線S/4～S/2的一定區域內。這是由于齒塊體在兩端受壓的狀態下會局部壓縮變形并上拱，在頂板區形成局部彎曲效應并在齒塊體形成核心受壓區。此外，橫隔板與齒塊錨固端交界處由于隔板彎曲效應產生了壓應力集中，由此亦反映出橫隔板提供給齒塊一個較大的反向支承力。

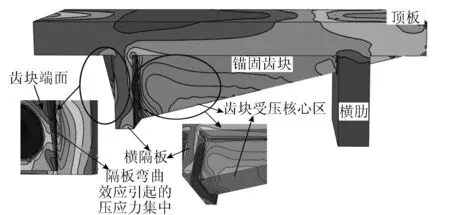
圖4 錨固區壓應力分布特征Fig.4 Distribution characteristics of compressive stress in anchorage zone

3 隔板參數分析與討論

隔板連通式齒塊與常規獨立三角齒塊最大的不同在于齒塊前后隔板提供的錨固支承作用，而已有研究僅分析了壁板厚度、鋼束轉向方式以及是否設錨前隔板(本研究中的橫肋)對錨固區受力效應的影響，但忽略了是否設錨端隔板(本研究中的橫隔板)、橫隔板寬度、橫隔板間距對錨固區受力效應的影響。以簡化的分析模型為基礎對隔板連通式齒塊的隔板參數進行分析。

考慮到UHPC的抗壓強度在150 MPa以上，而有限元中非錨墊板區的壓應力值不足70 MPa，未達到其抗壓強度的1/2，因此參數分析中不再考慮隔板參數對錨固區受壓性能的影響，僅分析錨固區的拉應力情況。根據錨固區的幾種典型局部效應確定拉應力分布的不利點(見圖5)。其中A，B，D，I，G點以及H點均位于齒塊縱向中心線上，I點距橫隔板中線250 mm，G點位于橫隔板與橫肋的正中間，距離橫隔板中線750 mm(該值的確定以橫隔板與橫肋之間的間距S=1.5 m時為基礎，當S變化時，I，G點的位置根據比例類推)。考慮錨固區的應力集中區域有一定的范圍(取值原則為取小區域的最大值)，限于篇幅各關注點詳細的位置情況未逐點解釋說明，可根據圖5中所示位置獲知。

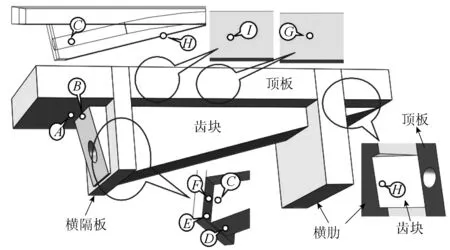
圖5 “隔板連通式齒塊”關注點位示意圖Fig.5 Schematic diagram of key points for DABIAS

3.1 隔板設置情況的影響

以簡化的分析模型為基礎，保持橫隔板與橫肋之間的間距S=1.5 m不變，橫隔板寬度L取1.2 m。設置了4種錨固方案進行對比分析：方案1為設計中隔板連通式齒塊錨固方案，方案2在方案1的基礎上取消了錨固處的橫肋(保留橫隔板)，方案3在方案1的基礎上取消了錨固處的橫隔板(保留橫肋)，方案4在方案1的基礎上取消了錨固處橫隔板與橫肋。

根據有限元分析(FEA)結果，將各隔板設置情況下齒塊錨固區關注點的應力值列入表1中(表中縱向應力(Longitudinal Stress)由L.S表示；橫向應力(Transversal Stress)由T.S表示；豎向應力(Vertical Stress)由V.S表示，下同)，表中只列出了與局部效應有關方向上的應力值。

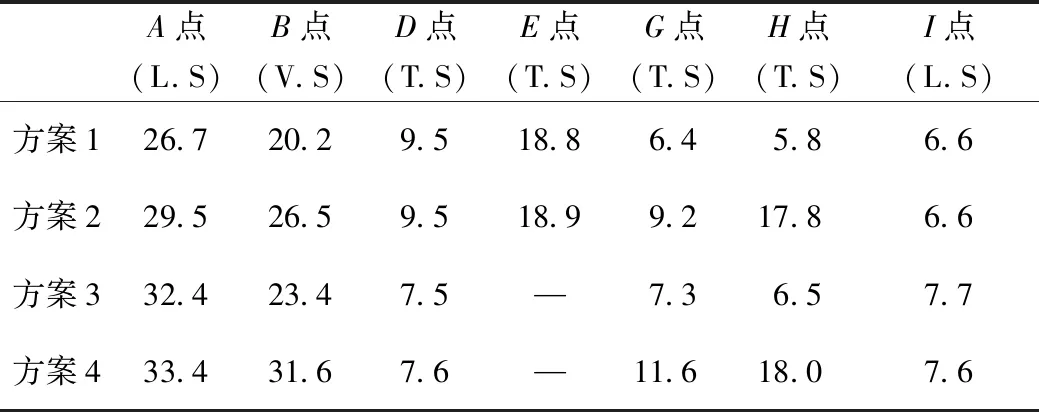
表1 各方案關注部位最大主拉應力值(單位：MPa)Tab.1 maximum principal tensile stress of each point in different schemes (unit: MPa)

根據表1可知，方案1(隔板連通式齒塊)與方案4(常規獨立三角齒塊)相比，A點的縱向拉應力值減小了20.1%，B點的豎向拉應力值減小了36.1%，G點的橫向拉應力值減小了44.8%，H點的橫向拉應力值減小了67.8%，I點的縱向拉應力值減小了13.2%。因此將齒塊錨固在橫隔板與橫肋上可降低錨固區的錨后牽拉效應、懸臂效應、局部彎曲效應和徑向力效應，且大大降低了錨固區的最大主拉應力值。方案2與方案4相比，A點的縱向拉應力值減小了11.7%，B點的豎向拉應力值減小了16.1%，D點的橫向拉應力值增加了25.0%，G點的橫向拉應力值減小了20.7%，H點的橫向拉應力值基本無變化。因此僅將齒塊錨固在橫隔板上可以降低錨固區的錨后牽拉效應、懸臂效應、局部彎曲效應，但對徑向力效應影響不大，且會增強錨下劈裂效應。方案3與方案4相比，無錨固橫隔板對錨固區的錨后牽拉效應、錨下劈裂效應的影響不大，但由于橫肋的作用能顯著降低錨固區的懸臂效應、局部彎曲效應和徑向力效應。綜上可述，隔板連通式齒塊相較于常規的獨立三角齒塊錨固性能更優，大大減小了錨固區的局部效應。

由于頂板中線部位的G,I點在縱橋向和橫橋向的應力值變化趨勢存在差異，為此，將方案1錨固區中頂板中心線位置上緣各點的橫向、縱向拉應力情況列如圖6中，以便更好地獲知隔板連通式齒塊錨固區的局部彎曲效應。圖中橫坐標軸0點對應錨固處橫隔板的中線位置，1 500 mm坐標對應橫肋的中線位置，3 000 mm坐標對應錨固后端橫隔板的中線位置。

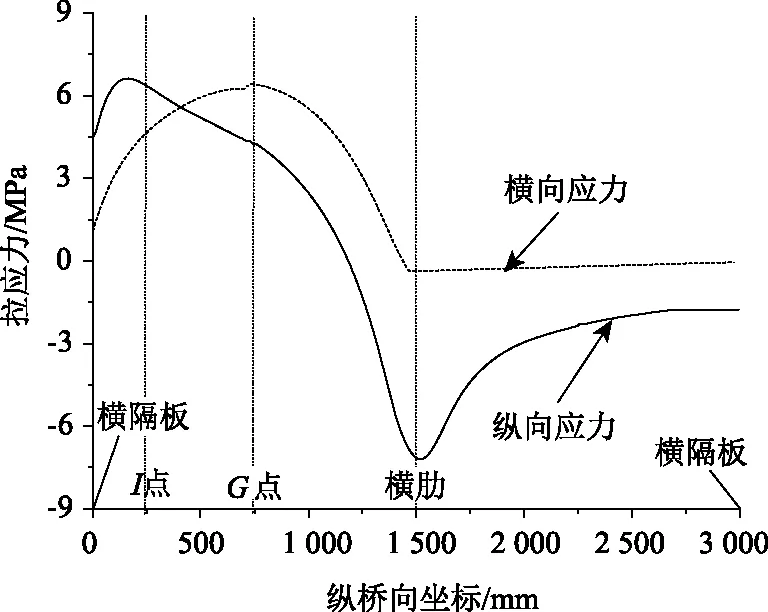
圖6 齒塊中心線位置頂板上緣各點的橫向、縱向應力Fig.6 Transversal and longitudinal stresses at each point on top edge of top plate in center-line position of anchor block

由圖6可知，錨固區橫隔板與橫肋之間頂板區域各點的橫橋向、縱橋向拉應力成波形分布(應力值先增大后減小，在橫肋位置達到最小值)。但G,I點的應力峰值點并未處于同一點，由此說明局部彎曲效應不只體現在一個方向的應力，但以往的研究往往只關注了頂板區域的縱橋向應力[1-5]，而橫橋向的局部彎曲效應應引起同樣的重視。此外，頂板錨固區的拉應力集中部位僅分布于橫肋坐標軸以左，由此說明頂板錨固區的鋼筋布置僅需考慮橫肋中心線以左的部位。

3.2 隔板寬度的影響

保持橫隔板與橫肋之間的間距S=1.5 m不變，橫隔板寬度L取為(n×b)mm(b為錨固齒塊的寬度，取值為400 mm，n依次取值為2，3，4，6，8，10)，橫隔板寬度的增加也意味著箱梁寬度的增加。根據FEA結果將各關注點的主拉應力值隨橫隔板寬度的變化情況列如圖7中，圖中均只列出了關注點應力較大方向上的主拉應力值，下同。

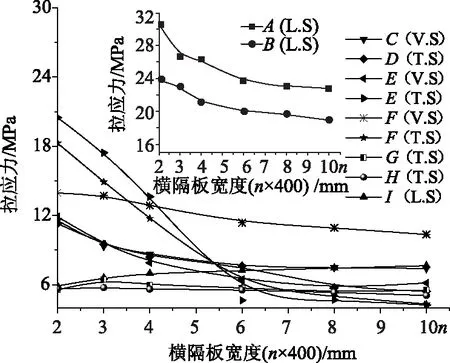
圖7 拉應力值隨橫隔板寬度的變化情況Fig.7 Tensile stress varying with diaphragm width

由圖7可知，A點～F點的應力均隨橫隔板寬度的增加而下降明顯，由此說明增大橫隔板寬度可以有效降低錨固區的錨后牽拉效應、懸臂效應、錨下劈裂效應以及隔板彎曲效應。但當橫隔板寬度達到齒塊寬度的6倍以上時，下降幅度則不再明顯。H點應力值隨橫隔板寬度的增加而變化幅度不大，即橫隔板寬度對錨固區徑向力效應的影響不大。I點應力隨橫隔板寬度的增加而增加，因此增加橫隔板的寬度會略微增加錨固區局部彎曲效應。

綜合上述分析，設計時保證橫隔板寬度在6b以上能大大降低錨固區的局部效應，特別是對于錨后牽拉效應、錨下劈裂效應以及隔板彎曲效應。

3.3 隔板間距的影響

在圖2的基礎上保持橫隔板寬度L=8b(3.2 m)不變，橫隔板與橫肋之間的間距S取1，1.5，2.0，2.5，3 m。各關注點拉應力值隨間距S的變化情況如圖8所示。

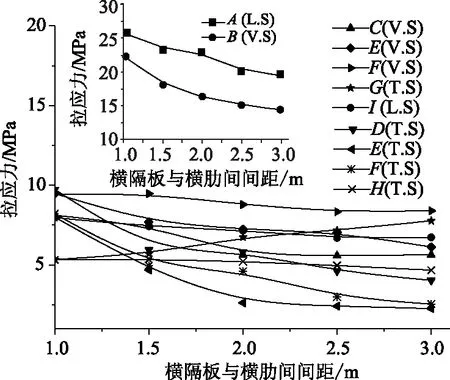
圖8 拉應力值隨橫隔板與橫肋間間距的變化情況Fig.8 Tensile stress varying with spacing between diaphragm and transverse rib

由圖8可知，A，B點的拉應力值隨隔板間距的增加而下降顯著，由此說明增大隔板間距可以有效降低錨固區的錨后牽拉效應、懸臂效應。C～F點的拉應力值隨隔板間距的增加而下降，但當隔板間距達到2 m以上時，應力變化幅度不明顯，由此說明當隔板間距較小時，劈裂效應和隔板彎曲效應才與隔板間距密切相關。G點的拉應力值隨隔板間距的增大而增大，說明隔板間距的增加會增大錨固區的局部彎曲效應。H點的應力值隨隔板間距的增加而變化不大，隔板間距對徑向力效應基本無影響。

基于上述分析，設計時橫隔板與橫肋間的間距不宜太小，綜合考慮橫隔板在整個箱梁中的作用(如抵抗扭轉、畸變等)[10]，間距S宜控制在1.5～2.5 m為宜。或者當箱梁不設置橫肋時齒塊僅錨固在橫隔板上，則錨固處相鄰橫隔板可替代橫肋，此時，相鄰橫隔板之間的間距宜控制在3.0～5.0 m。

4 多齒塊錨固對局部效應的影響

進一步地，開展同一橫隔板處多齒塊錨固及齒塊間距對錨固區局部效應的影響研究。基于圖2模型，設計了5種齒塊間距，分別為0，1，2，4，6 m。橫隔板與橫肋之間的間距S取1.5 m，橫隔板寬度L取8.96 m。為便于與對稱單齒塊錨固進行對比分析(例如圖8中橫隔板寬度等于6b時)，將該模型中關注齒塊縱向中心線距腹板內邊緣的距離定為1.2 m(3b)，參數分析中該齒塊位置不加以改變，僅變化另一齒塊的位置，間距為0時即為非對稱單齒塊錨固。

根據FEA結果將各關注點應力值隨相鄰齒塊間間距的變化情況列如圖9中，圖中C，E點位于關注齒塊中近腹板側，C′，E′與C，E點關于齒塊中心線對稱。

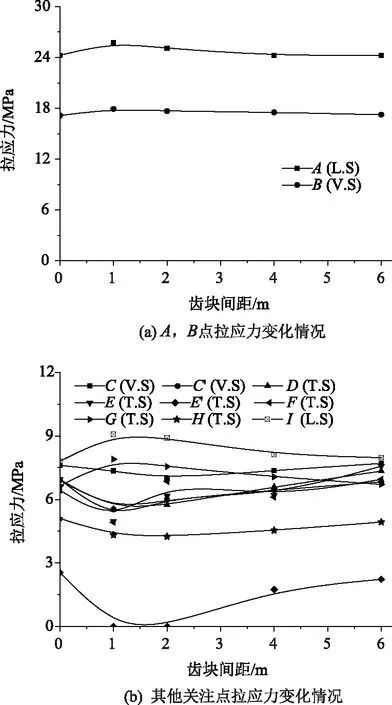
圖9 拉應力值隨相鄰齒塊間間距的變化情況Fig.9 Tensile stress varying with spacing between adjacent anchor blocks

由圖9可知，同一錨固隔板上雙齒塊錨固對錨固區的最大拉應力值影響不大(增幅6.2%)。同時，設置雙齒塊會降低橫隔板和齒塊部位的拉應力值，特別是當齒塊相距為1 m時，齒塊相鄰側的橫隔板部位的拉應力值接近于0。這是由于在雙齒塊的協同作用下齒塊間的橫隔板與齒塊變形協調，導致隔板彎曲效應大大降低。當齒塊間距逐漸增大時，齒塊間的變形協調效應變得不明顯，逐漸轉變為單齒塊作用。此外，E點的應力值要顯著大于E′點的應力值(絕對值均較小)，說明在同一錨固體系中隔板彎曲效應與齒塊所處位置息息相關，越靠近腹板，作用效應越顯著。但設置雙齒塊會增加頂板上緣的拉應力值(增加了18.8%)，而當齒塊間距逐漸增大時，對局部彎曲效應的影響程度會有所下降，特別是當間距S達到6 m時，其影響基本為0。

綜上可知，對于隔板連通式齒塊，同一橫隔板上采用多齒塊錨固對錨固區的整體受力產生的負面影響較小。

5 拉壓桿模型及配筋設計

5.1 拉壓桿模型

考慮到目前國際上尚無針對UHPC箱梁橋隔板連通式齒塊拉壓桿模型的相關設計規定，以及隔板連通式齒塊5種典型局部效應與獨立三角齒塊較為接近，因此可參考獨立三角齒塊的部分規定[5,16-18]、已有案例[4,19]以及本錨固方式下的應力等值線(圖3、圖4)及應力跡線分布特征(圖10)構建拉壓桿模型，如圖11所示。

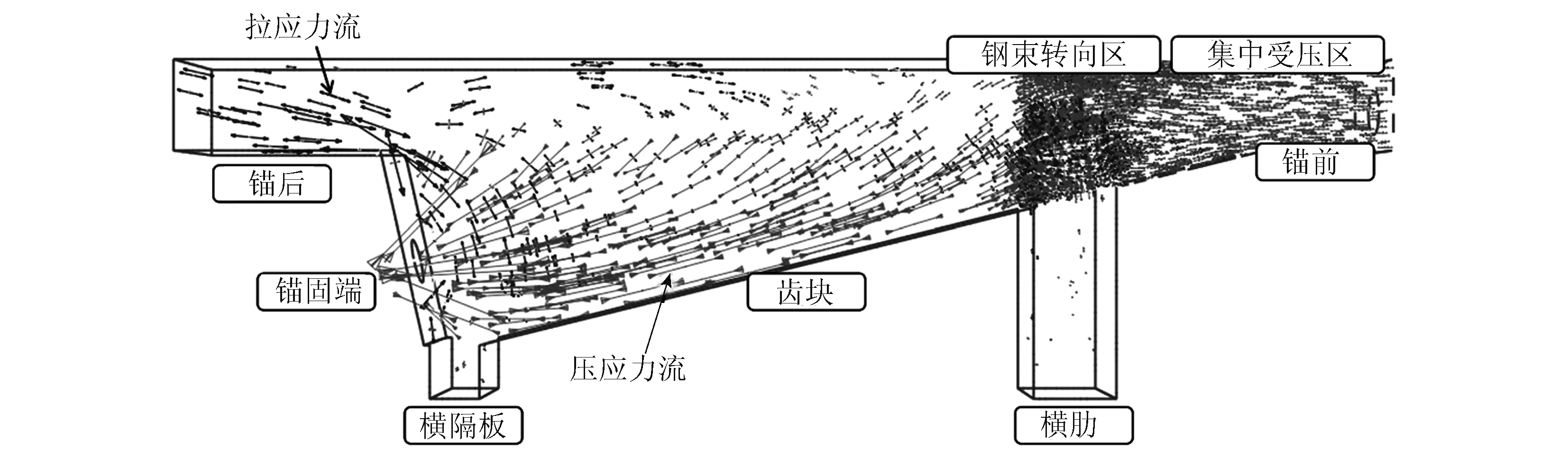
圖10 錨固區應力跡線分布圖Fig.10 Distribution of stress traces in anchorage zone

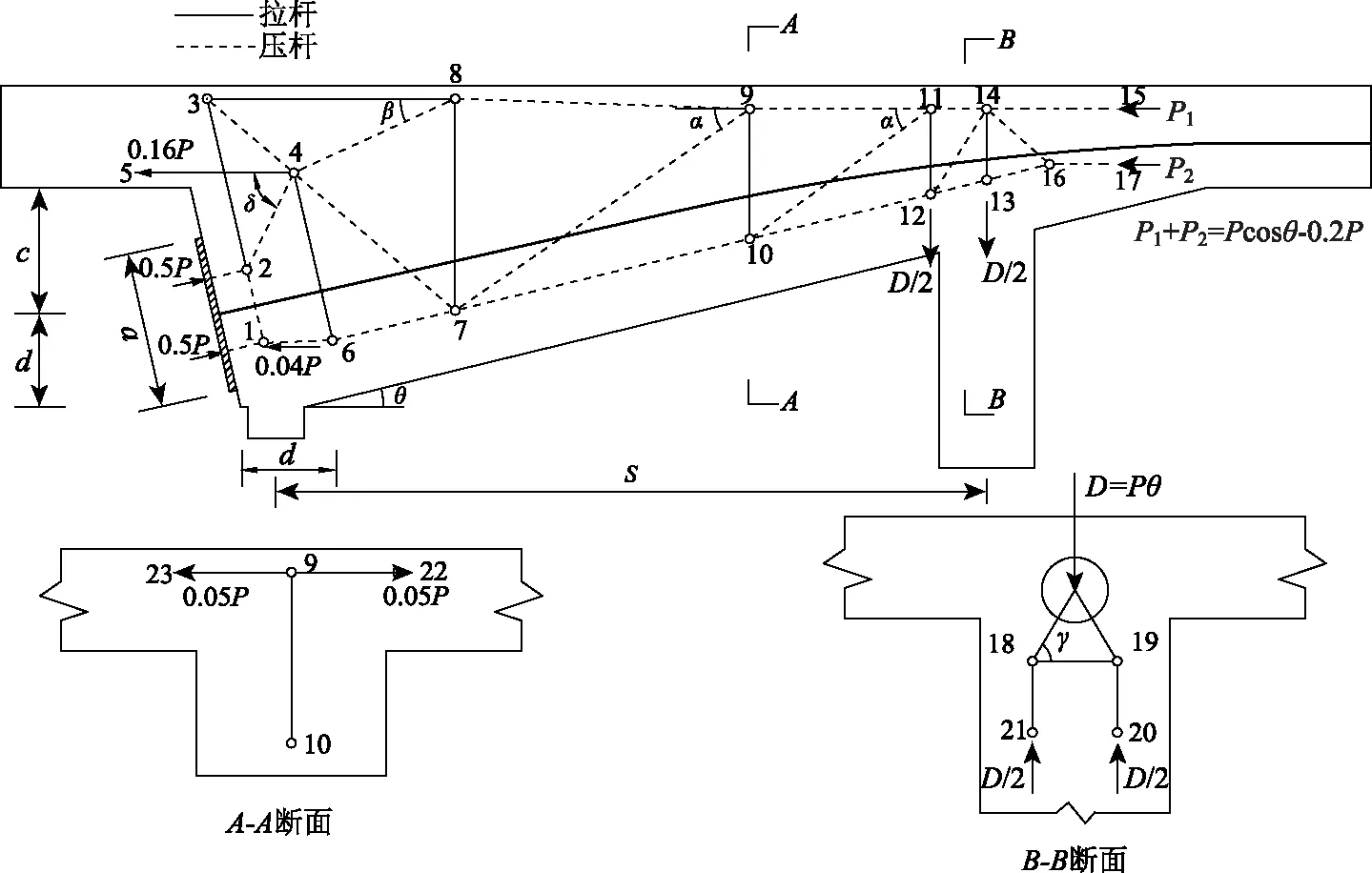
圖11 錨固區拉壓桿模型Fig.11 Strut-and-tie model for anchorage zone

局壓錨固區拉壓桿模型的基本構形及設計符合以下規定：

(1)根據JTG—2018[5]的規定將1～2壓桿至錨固區的距離取為0.25倍錨墊板寬度，1，2號節點的間距取0.5倍錨墊板寬度，由此可確定1，2號節點的位置。

(2)力筋軸線與齒塊縱向邊緣之間均勻分布的壓應力場通過平行于齒塊縱向邊緣的壓桿來模擬，將壓桿邊距取為0.25倍齒塊高度。根據規范[5]錨下劈裂效應作用位置至錨固端面的水平距離d與錨固張拉力中心至齒塊下邊緣的垂直距離相等的原則可確定6號節點位置。

(3)根據應力等值線圖3，7號節點處于距離橫隔板中心線S/4～S/2的核心受壓區內，由此可確定7號節點。4～6號拉桿表示錨下劈裂應力區，已有的研究認為[20]錨下拉桿位置與劈裂應力合力點位置一致時可實現對劈裂開裂的有效控制。基于此并考慮與抵抗錨后牽拉效應的4～5節點重合可確定4號節點位置(4號節點為彌散型節點，必定位于頂板內且靠近與齒塊的交界處部位，起到主應力轉向作用)。

(4)根據規范[18]的建議，規定4～8壓桿與水平向拉桿的傾角β在25°～65°范圍內取值可避免壓桿在壓力作用下強度過于軟化，建議取下限值25°(可確定7，8號節點)，由此可得到該區域豎向拉桿抵抗縱向剪力的最小配筋量。此處豎向拉桿7～8之所以能抵抗齒塊與壁板交界區域的縱向剪切破壞是由于豎向拉桿與斜壓桿之間組成了協同作用機制。

(5)為避免預應力荷載傳遞過程中錨固齒塊與頂板的交界面產生剪切破壞，界面剪力Vu與豎向壓力N需滿足Vu≤μN的關系式，其中Vu，N分別表示(混凝土)斜壓桿內力的水平與豎直分力。根據AASHTO規范[17]壁板與齒塊交界面的摩擦系數取1.4，因此斜壓桿傾角α不應小于arctan(1/μ)。在36°附近取值，可得到錨固區抗剪所需的最小鋼筋計算量。進一步地，根據力流傳遞規律可得到9～12號節點。

(6)考慮橫肋對徑向力的支承作用，因此將13，14號節點布置于橫肋的中心線上。壓桿12～14，14～16僅起到對拉桿13～14的錨固作用，而不影響拉桿本身內力的計算，因此16號節點位置可根據P2受力情況微調。

(7)徑向力按JTG—2018[5]中預應力鋼筋轉向前后的切線夾角(rad)與錨固張拉力的乘積取值，即D=Pθ。橫肋提供的豎向反力根據表1計算結果偏保守地取值為徑向力的50%，因此徑向區的箍筋配置量也可大大減少。徑向力傳遞過程中斜壓桿與橫向拉桿之間的夾角γ應盡可能大，以發揮齒塊中預應力孔道下緣橫向受拉鋼筋的抗裂作用。

(8)根據JTG—2018[5]獨立三角齒塊錨后牽拉力設計值取錨固力設計值大小的20%，但隔板連通式齒塊由于橫隔板以及橫肋提供的水平向支承力可分擔部分錨后牽拉力。根據參數分析結果(表1)近似取錨后牽拉力的20%。因此，本模型錨后牽拉力設計值取錨固力設計值大小的16%，橫隔板以及橫肋提供一個4%錨固力設計值大小的水平向支反力，錨前頂板部分則分擔剩余的水平向支反力。

(9)根據應力等值線圖3以及頂板上緣各點的橫向、縱向應力圖6，局部彎曲效應作用區域位于橫隔板與橫肋中間部位。本模型中局部彎曲效應橫向拉力特征通過9～22桿和9～23桿模擬，橫向拉力值根據參數分析結果(圖7、圖8)偏保守地取錨后牽拉力的1/3，即0.05P。

5.2 配筋設計——算例

以背景工程為例進行配筋設計，抗裂鋼筋的配筋量取值由上述拉壓桿模型中拉桿內力控制。參照規范JTG—2018[5]的建議按照極限狀態法進行錨固區的配筋設計，所需配筋量為：

As=T/fsd,

(1)

式中，As為配筋面積；T為拉桿內力設計值；fsd為普通鋼筋抗拉強度設計值(HRB400鋼筋按規范[5]取330 MPa)。

由于已有的規范中錨固區配筋設計均未考慮混凝土抗拉強度的貢獻，因此本算例配筋設計亦僅將UHPC的抗拉強度作為一種安全儲備(UHPC的直接拉伸強度一般超過7 MPa，抗折強度超過30 MPa)，但也不再對鋼筋強度進行折減。由于UHPC具有超高的抗壓強度(一般超過150 MPa)，因此對壓桿不再加以驗算。背景工程中預應力鋼束采用19束1860型φ15.2 mm鋼絞線，按70%的控制張拉力計算，則預應力設計值為3 463 kN。錨固力設計值為1.2倍的預應力設計值，則錨固力設計值P為4 156 kN。

以上述拉壓桿模型(圖11)為基礎，利用桁架計算理論計算各拉桿內力，可得到背景工程中隔板連通式齒塊的拉壓桿模型，如圖12所示。

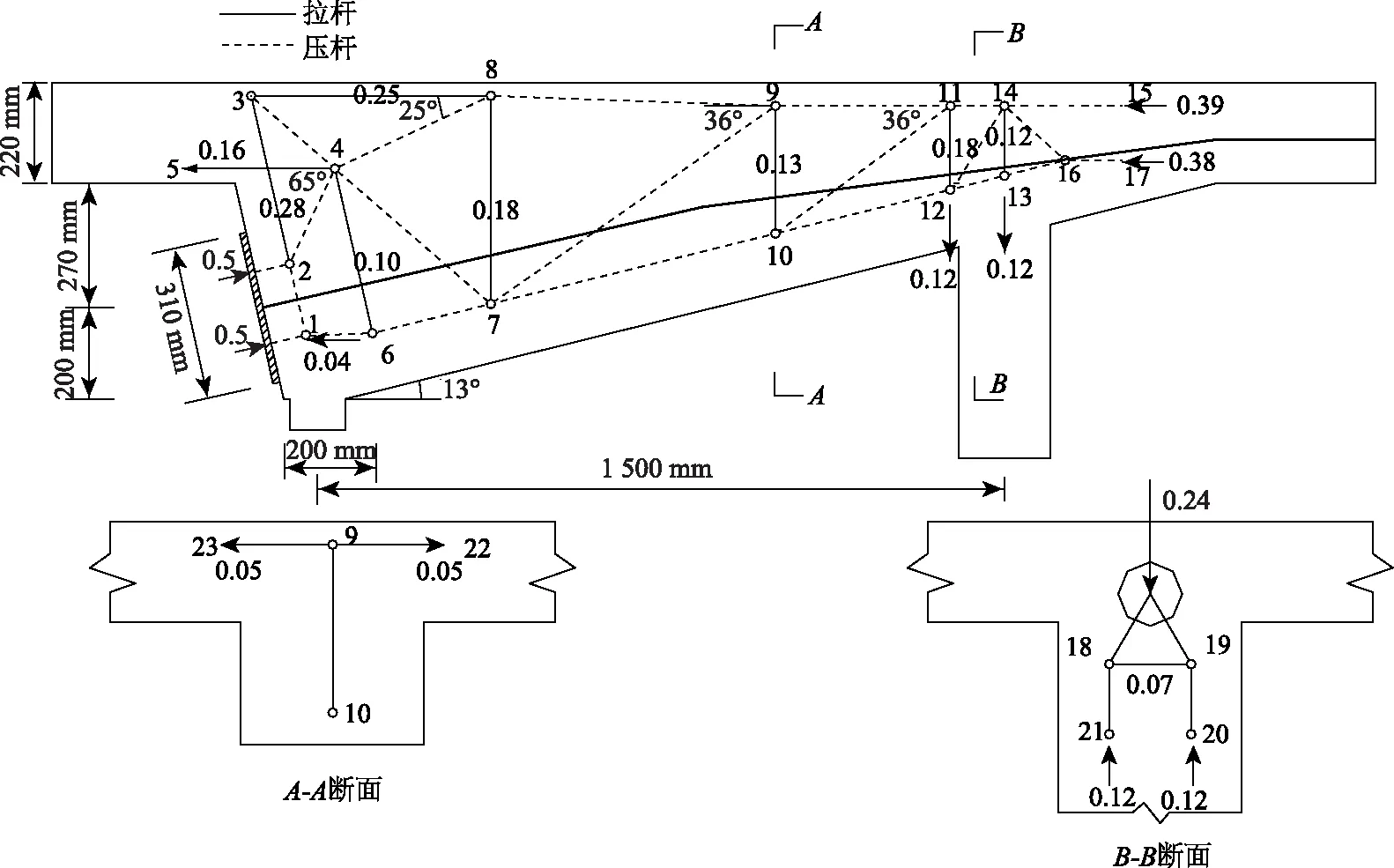
圖12 背景工程中齒塊錨固區拉壓桿模型Fig.12 Strut-and-tie model for anchorage zone in background project

結合規范[5,17]對齒板錨固區關鍵受力部位進行配筋設計，如圖13所示，錨固區配筋量計算情況如表2所示。配筋設計簡述如下：(1)齒塊錨下配置抵抗劈裂效應的閉合式箍筋，間距為100 mm，縱向范圍取1.2倍齒塊高度，并將箍筋插入到頂板區域與頂板縱筋形成鋼筋網；(2)懸臂效應的拉應力方向以及受力范圍與錨下劈裂效應基本一致，因此設計為同類鋼筋共同受力，視為整體進行配筋；(3)錨后牽拉效應在橫向上以錨固點為中心向兩側不斷衰減，其配筋設計的橫向分布范圍取預應力鋼筋軸線兩側各1.5倍齒塊寬度范圍內，鋼筋間距為100 mm，為充分發揮錨后鋼筋的抗裂作用，錨固鋼筋長度取2.5 m；(4)根據前文計算結果(圖7～圖9)，實際上局部彎曲效應拉應力值較小，遠小于錨后牽拉效應，且應力跡線圖10也表明兩種局部效應在頂板區域的界限不明顯，因此配筋設計時將兩種效應視為整體進行配筋；(5)在頂板橫向部位布置2層鋼筋與頂板縱向鋼筋形成鋼筋網絡，亦用于抵抗局部彎曲作用的橫向拉力，橫向分布范圍取力筋軸線兩側各1.5倍齒塊寬度范圍內；(6)預應力鋼束轉向區配置少量閉合式箍筋，分擔部分豎向力及橫向拉應力。

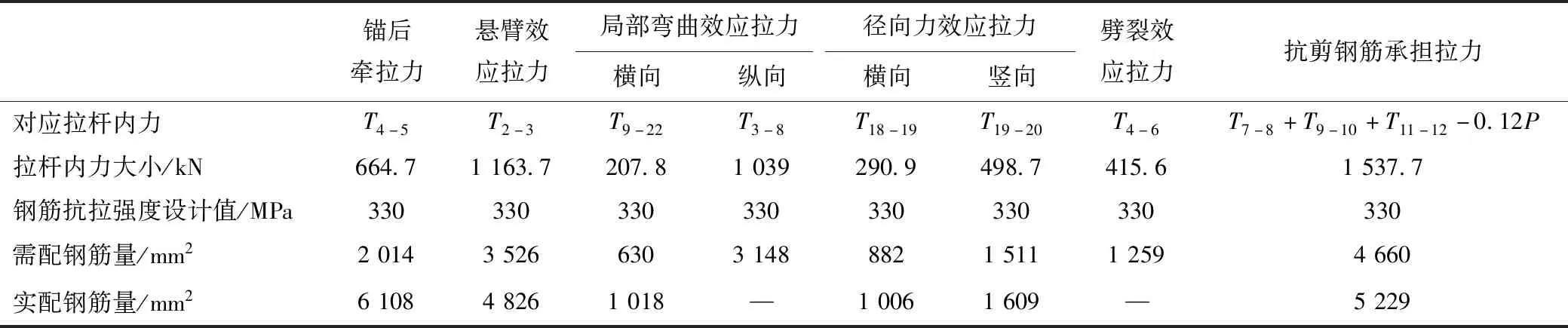
表2 錨固區配筋量計算Tab.2 Reinforcement calculation for anchorage zone

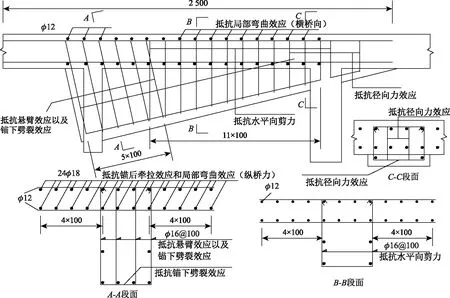
圖13 錨固區的配筋設計(單位：mm)Fig.13 Reinforcement design for anchorage zone (unit: mm)

6 結論

(1)通過應力等值線分析，揭示了隔板連通式齒塊錨固區的6種典型局部效應，即錨下劈裂效應、錨后牽拉效應、局部彎曲效應、徑向力效應和懸臂效應以及橫隔板部位的隔板彎曲效應，其中局部彎曲效應在縱橋向和橫橋向的拉應力集中均較為明顯。

(2)橫隔板與橫肋之間的齒塊壓應力沿縱橋向先逐漸增大隨后逐漸減小，存在核心受壓區，位于距離橫隔板中心線S/4～S/2的范圍內(S為橫隔板與橫肋之間的距離)。

(3)相比于常規獨立三角齒塊，隔板連通式齒塊可大大降低錨固區的拉應力集中情況。增大橫隔板寬度及隔板間間距能有效降低錨固區的局部效應，但當隔板寬度超過6倍齒塊寬度時、隔板間距超過2 m 時，下降趨勢變得不明顯。同一橫隔板在多齒塊錨固下對錨固區的負面影響較小，特別地，當齒塊間距逐漸增大到6 m時，雙齒塊錨固效應逐漸轉變為單齒塊錨固效應。

(4)基于局部效應分析結果、力流特征以及力流平衡關系提出了UHPC箱梁隔板連通式齒塊錨固區拉壓桿模型的基本構建方法，并通過算例展示了密集橫隔板UHPC箱梁錨固區配筋設計過程，適用于該類錨固方式的工程設計。