系統(tǒng)規(guī)劃 整體理解

鐘鳴

一、教材分析

蘇科版七年級上冊教材共6章：第1章“數(shù)學(xué)與我們同行”，介紹數(shù)學(xué)學(xué)習(xí)的基本內(nèi)容和方式;第2章“有理數(shù)”，介紹數(shù)的擴(kuò)充及其運(yùn)算;第3章“代數(shù)式”，介紹代數(shù)式及其運(yùn)算，從算術(shù)計(jì)算到代數(shù)運(yùn)算，體會代數(shù)思想;第4章“一元一次方程”，用代數(shù)式刻畫等量關(guān)系產(chǎn)生方程，用方程解決問題，體會方程思想、建模思想;第5章“走進(jìn)圖形世界”，介紹幾何學(xué)習(xí)的基本內(nèi)容和方式;第6章“平面圖形的認(rèn)識（一）”，介紹平面幾何的基本對象及其性質(zhì)，掌握幾何基本技能。整體可分為三個部分：第1章是從初中數(shù)學(xué)學(xué)習(xí)全局的角度為學(xué)生呈現(xiàn)初中數(shù)學(xué)學(xué)習(xí)的全貌;第2-4章是從小學(xué)的算術(shù)思維走向初中的代數(shù)思維，從小學(xué)的具體形象走向初中的一般抽象;第5-6章是從小學(xué)直觀的實(shí)驗(yàn)幾何走向初中的論證幾何。

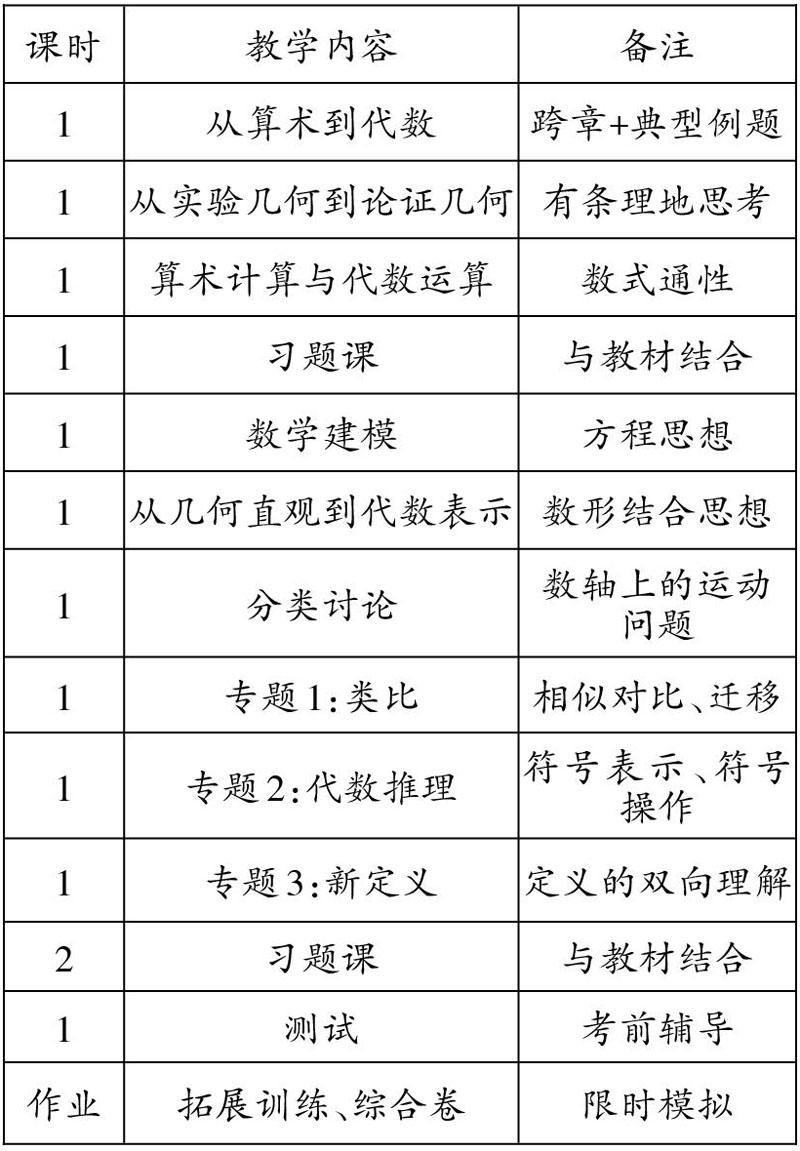
教師在期末復(fù)習(xí)的時候要想讓學(xué)生形成整體理解，就需要幫助學(xué)生打通各章之問的藩籬，溝通知識之問的聯(lián)系，形成跨章視野，融會貫通（這一點(diǎn)與單元復(fù)習(xí)不同）。本節(jié)課作為期末復(fù)習(xí)的第一課時，應(yīng)該對一學(xué)期所學(xué)內(nèi)容作一個總覽式回顧，在此基礎(chǔ)上形成系列的期末復(fù)習(xí)計(jì)劃，如右表。

二、學(xué)情分析

學(xué)生印象深的是最近所學(xué)的幾何內(nèi)容，對于前面的數(shù)與代數(shù)的內(nèi)容有所遺忘。教師應(yīng)通過一些基本題，喚起學(xué)生的相關(guān)記憶，激活相應(yīng)的技能。學(xué)生往往習(xí)慣于零碎的眼前知識，而忽視整體的系統(tǒng)，這就需要教師有意識地引導(dǎo)學(xué)生對所學(xué)習(xí)的整冊內(nèi)容形成整體認(rèn)識。學(xué)生喜歡在具體的問題中進(jìn)行有線索的思考，不喜歡簡單的回憶和空洞的敘述。因此，本節(jié)課應(yīng)該通過具體的問題喚醒學(xué)生的回憶，通過問題鏈幫助學(xué)生形成整體認(rèn)識。本節(jié)課學(xué)生的學(xué)習(xí)難點(diǎn)是在對相關(guān)知識的對比中深入理解知識，形成整體認(rèn)識。

三、目標(biāo)分析

教學(xué)目標(biāo)：形成全冊書的總體結(jié)構(gòu);理解各章的內(nèi)在聯(lián)系;澄清相關(guān)知識認(rèn)識誤區(qū)，理解相關(guān)知識的本質(zhì)。

達(dá)成標(biāo)志：學(xué)生能有順序地說出全冊知識;能說出各章之間的聯(lián)系;能分辨具體問題中的易混淆概念。

四、教學(xué)過程

1.問題情境。

問題1：本冊書都學(xué)習(xí)了哪些內(nèi)容？

問題2：依據(jù)你的理解，怎么將這6章分類？

設(shè)計(jì)意圖：站在學(xué)習(xí)結(jié)束的終點(diǎn)，回頭復(fù)習(xí)所學(xué)內(nèi)容，通過不同學(xué)生的相互補(bǔ)充，喚起全班學(xué)生對全冊內(nèi)容的回憶，為思考分類鋪墊;引發(fā)學(xué)生對不同分類觀點(diǎn)的質(zhì)疑，最終達(dá)成共識，將全冊內(nèi)容分為三個部分。

2.任務(wù)導(dǎo)學(xué)。

活動1：數(shù)的認(rèn)識歷程。

問題3：請回憶并舉例說明，從小學(xué)到初中，我們認(rèn)識的數(shù)發(fā)生了什么樣的變化。

設(shè)計(jì)意圖：教師通過學(xué)生舉例的不斷豐富，借助點(diǎn)評，帶領(lǐng)學(xué)生梳理“從0、正整數(shù)、正分?jǐn)?shù)（與正小數(shù)的區(qū)別和聯(lián)系），到負(fù)整數(shù)、負(fù)分?jǐn)?shù)（與負(fù)小數(shù)的區(qū)別和聯(lián)系），再到整數(shù)范圍大、分?jǐn)?shù)范圍擴(kuò)大（與小數(shù)相區(qū)別）”的認(rèn)識歷程。

追問1：整數(shù)與分?jǐn)?shù)有什么共同點(diǎn)？

設(shè)計(jì)意圖：溝通整數(shù)、分?jǐn)?shù)、有理數(shù)之間的聯(lián)系，讓學(xué)生認(rèn)識到它們能統(tǒng)一成分?jǐn)?shù)形式，所以把整數(shù)和分?jǐn)?shù)統(tǒng)一叫作有理數(shù)。

例：給出下列各數(shù)，-7，10.1，1.212112111…，..389，0，-0.67，13/5，π。請分出正數(shù)、負(fù)數(shù)、整數(shù)、分?jǐn)?shù)、無理數(shù)。

設(shè)計(jì)意圖：復(fù)習(xí)數(shù)的不同分類，理解有理數(shù)和無理數(shù)的根本區(qū)別是，有理數(shù)是有限小數(shù)、無限循環(huán)小數(shù)，無理數(shù)是無限不循環(huán)小數(shù)。

練一練：題目略。

設(shè)計(jì)意圖：通過練習(xí)，鞏固對數(shù)的認(rèn)識。

追問2：數(shù)的范圍擴(kuò)大了，原來的運(yùn)算法則和運(yùn)算律是否發(fā)生變化？如果是，那么發(fā)生了什么樣的變化？請舉例說明。

設(shè)計(jì)意圖：通過舉例，對比有理數(shù)運(yùn)算法則與小學(xué)運(yùn)算法則的異同和轉(zhuǎn)化關(guān)系，復(fù)習(xí)運(yùn)算法則和運(yùn)算律。

問題4：觀察下列兩個算式，說說你的觀察結(jié)果。

7 （1）（-5/8-1/6+7*12）×24+s;（2）（-4）2×（-3/4）+30/（-6）。

設(shè)計(jì)意圖：在這個活動中指導(dǎo)學(xué)生先從整體結(jié)構(gòu)觀察，再從局部細(xì)節(jié)觀察;經(jīng)歷運(yùn)算能力生成的細(xì)致過程：通過觀察理解運(yùn)算對象，確定運(yùn)算順序，選擇運(yùn)算方法，依據(jù)法則運(yùn)算，檢驗(yàn)運(yùn)算結(jié)果。

問題5：化簡求值，5（3a2b-a2b）-4（-a2b+3a2b），其中a=-l，b=-2。

師：觀察一下，你能發(fā)現(xiàn)代數(shù)式有什么特征？

學(xué)生首先發(fā)現(xiàn)的是有“同類項(xiàng)”并進(jìn)行了說明，但這只是局部的特征，學(xué)生還想不到從整體觀察。

師：你們是從局部觀察的。從整體上看，你能發(fā)現(xiàn)什么特征？

學(xué)生發(fā)現(xiàn)整體結(jié)構(gòu)是5A-4B。

師：再聚焦到A和B，你能發(fā)現(xiàn)什么特征？

學(xué)生終于發(fā)現(xiàn)A和B是一樣的，只要用“加法交換律”就可以解釋。于是，原代數(shù)式的結(jié)構(gòu)就是5A-4A，簡便方法出現(xiàn)了。

師：觀察是思維的入口，但是怎么觀察？既需要從局部細(xì)節(jié)入手，也要從整體結(jié)構(gòu)著眼，這樣就不會“一葉障目，不見泰山”，就能夠發(fā)現(xiàn)更為簡便的方法。

追問3：從算式到代數(shù)式，運(yùn)算法則和運(yùn)算律有何異同？

設(shè)計(jì)意圖：一方面，讓學(xué)生進(jìn)一步感悟觀察在代數(shù)式運(yùn)算中的重要性;另一方面，結(jié)合具體問題感悟數(shù)式通性：變化的和不變的。

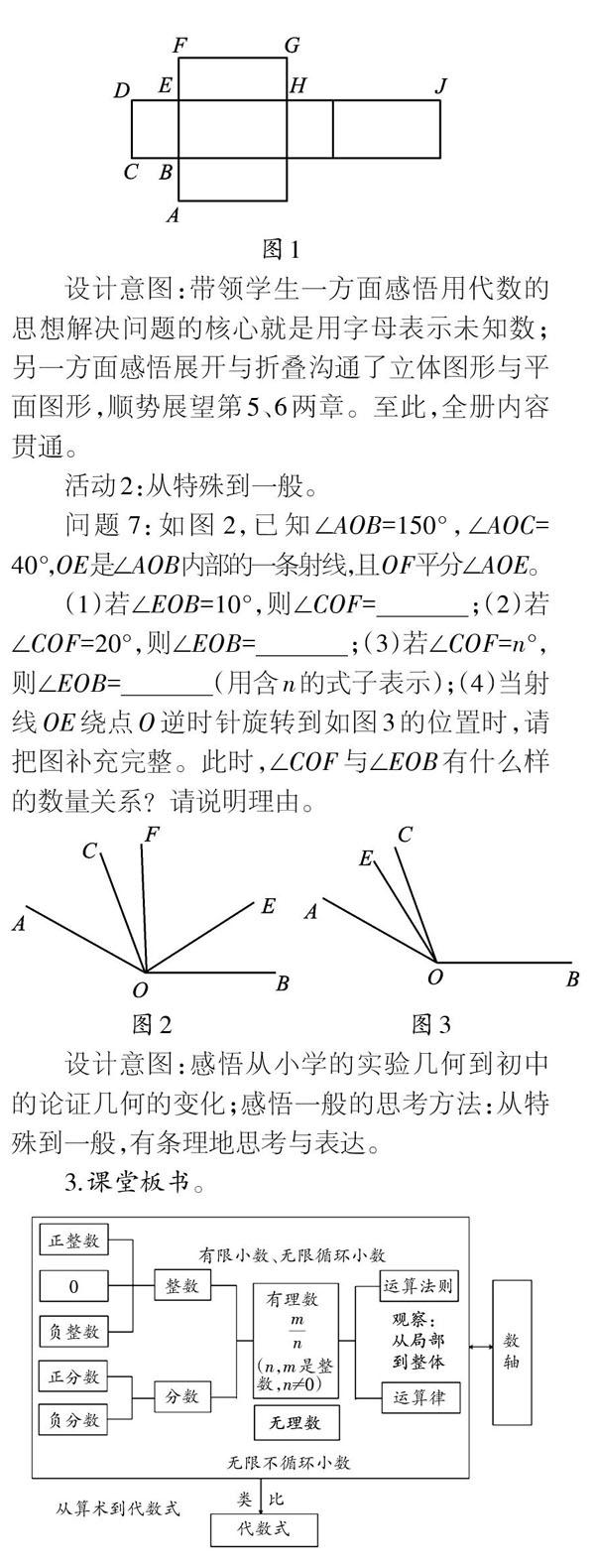
問題6：圖1是某長方體包裝盒的表面展開圖，這個長方體的長FG比寬DC多2cm，且AF的長為20cm，DJ的長為34cm，求這個長方體的表面積。

設(shè)計(jì)意圖：帶領(lǐng)學(xué)生一方面感悟用代數(shù)的思想解決問題的核心就是用字母表示未知數(shù);另一方面感悟展開與折疊溝通了立體圖形與平面圖形，順勢展望第5、6兩章。至此，全冊內(nèi)容貫通。

活動2：從特殊到一般。

問題7：如圖2，已知∠AOB=150°，∠AOC=40°，OE是∠AOB內(nèi)部的一條射線，且OF平分∠AOE。

（1）若∠EOB=10°，則∠COF=____ ;（2）若∠COF=20°，則∠EOB=____;（3）若∠COF=n°，則∠EOB=

（用含n的式子表示）;（4）當(dāng)射線OE繞點(diǎn)O逆時針旋轉(zhuǎn)到如圖3的位置時，請把圖補(bǔ)充完整。此時，∠COF與∠EOB有什么樣的數(shù)量關(guān)系？請說明理由。

設(shè)計(jì)意圖：感悟從小學(xué)的實(shí)驗(yàn)幾何到初中的論證幾何的變化;感悟一般的思考方法：從特殊到一般，有條理地思考與表達(dá)。

3.課堂板書。

4.課堂小結(jié)。

你覺得在本冊書的學(xué)習(xí)中，還有什么收獲值得分享？你將如何進(jìn)行接下來的期末復(fù)習(xí)？

設(shè)計(jì)意圖：引導(dǎo)學(xué)生分享一學(xué)期數(shù)學(xué)學(xué)習(xí)的感悟，啟發(fā)學(xué)生對接下來的期末復(fù)習(xí)自主進(jìn)行整體規(guī)劃，不斷地激發(fā)學(xué)生的自主學(xué)習(xí)意識。

五、教后反思

錢學(xué)森先生把系統(tǒng)看作由相互作用、相互依賴的若干部分結(jié)合而成的有機(jī)整體，也是它從屬的更大系統(tǒng)的組成部分。七（上）的數(shù)學(xué)內(nèi)容就是一個系統(tǒng)，又是其所從屬的初中數(shù)學(xué)大系統(tǒng)的組成部分。小學(xué)數(shù)學(xué)則是從屬于它的小系統(tǒng)。期末復(fù)習(xí)時，教師有必要通過系統(tǒng)規(guī)劃幫助學(xué)生形成整體理解，打通小學(xué)數(shù)學(xué)與初中數(shù)學(xué)的聯(lián)系。因此，本節(jié)課筆者重點(diǎn)比較了小學(xué)與初中在知識、方法和思想上的異同，讓學(xué)生感受成長的獲得感，而不只是“做題、講題、練題”。遺憾的是只完成了數(shù)與代數(shù)部分的溝通。活動2中小學(xué)實(shí)驗(yàn)幾何與初中論證幾何的對比未來得及展開，只能放入下一課重點(diǎn)體會。筆者經(jīng)過研究，認(rèn)為“后建構(gòu)課堂”是課堂教學(xué)活動的高級形式。期末復(fù)習(xí)是“后建構(gòu)課堂”的重要形式。系統(tǒng)規(guī)劃、整體理解是其基本特征。這種課堂能幫助學(xué)生建構(gòu)知識結(jié)構(gòu)、認(rèn)知結(jié)構(gòu)，感悟知識價值和思想方法，對所學(xué)內(nèi)容形成整體理解，更注重學(xué)習(xí)的系統(tǒng)規(guī)劃和知識的整體理解，更關(guān)注思維方式的訓(xùn)練、思維品質(zhì)的形成和數(shù)學(xué)素養(yǎng)的培育。

本文系江蘇省中小學(xué)教學(xué)研究第十三期重點(diǎn)資助課題“指向?qū)W科核心素養(yǎng)的數(shù)學(xué)‘后建構(gòu)課堂設(shè)計(jì)研究”（編號2019JK13-ZB16），江蘇省教育科學(xué)“十三五”規(guī)劃2018年度立項(xiàng)課題“‘概念圖在初中數(shù)學(xué)課堂教學(xué)中應(yīng)用的策略研究”（編號D/2018/02/177），無錫市教育科學(xué)規(guī)劃課題“促進(jìn)學(xué)生思維深度參與的中學(xué)數(shù)學(xué)課堂教學(xué)實(shí)踐研究”（編號D/D/2018/002）階段性研究成果。