思想在前 計算在后

文 張 鋒（特級教師）

數學之所以有生命力，就在于它有趣；數學之所以有趣，就在于它對思維的啟迪。概率統計中的問題同樣也是如此。下面我們一起來看兩個典型的數學思想在概率題中的應用。

一、方程思想

方程思想，就是利用問題中已知量與未知量之間的等量關系列出方程，從而得以解決問題的一種思想方法。與概率有關的計算問題，有時可以通過設未知數，根據概率的定義列出方程來解決。

例1在一個不透明的袋子中裝有2個黃球，3個黑球和5個紅球，它們除顏色外其他都相同。現再將若干個紅球放入袋中，與原來的10個球混合在一起，從袋中隨機摸出一個是紅球的概率為-請求出后來放入袋中的紅球的個數。

【分析】原來口袋中有10個球，其中紅球5個，設再往口袋中放入x個紅球，則現在紅球數為（x+5）個，球的總數為（x+10）個。根據概率的意義，紅球個數與球總個數的比值等于摸到紅球的概率列出方程，解方程便可求出后來放入口袋中的紅球個數。

解：設放入x個紅球，由題意得，解得x=5。經檢驗，x=5是原方程的根，且符合題意。

【小結】本題通過設紅球的個數，根據等可能性概率的計算公式列出方程，體現了方程思想在解決概率問題中的應用。

二、數形結合思想

所謂數形結合思想，就是在研究過程中，把“數”和“形”結合起來，使隱蔽的問題“明顯”化，抽象的問題“直觀”化，復雜的問題“簡單”化的一種解題思路。同學們在遇到有關圖形的概率計算時，應注意運用數形結合思想，對于涉及兩步或兩步以上的隨機事件的概率問題，可以畫樹狀圖（或列表）進行求解。

例2如圖1，四邊形ABCD是菱形，E、F、G、H分別是各邊中點，隨機向菱形ABCD內擲一粒米，則米粒落到陰影區域內的概率是________。

圖1

【分析】∵四邊形ABCD是菱形，E、F、G、H分別是各邊中點，易證得四邊形EFGH是矩形，且∴四邊形EFGH的面積為。

答案：。

【小結】解決本題的關鍵是先證得順次連接菱形各邊中點得到的四邊形是矩形，再借助三角形中位線找到矩形的邊長與菱形對角線的關系，進而找到矩形面積與菱形面積的關系，最后計算面積比求得概率。

小試牛刀

1.在一個不透明的袋子中裝有僅顏色不同的10個小球，其中紅球4個，黑球6個。

（1）先從袋子中取出m（m＞1）個紅球，再從袋子中隨機摸出1個球，將“摸出黑球”記為事件A。請完成下列表格：

事件A m的值必然事件 隨機事件

（2）先從袋子中取出m個紅球，再放入m個同樣的黑球并搖勻，若隨機摸出1個球是黑球的概率等于，求m的值。

2.如圖2，平行四邊形ABCD的對角線AC、BD交于點O，EF、GH過點O，且點E、H在邊AB上，點G、F在邊CD上，向平行四邊形ABCD內部投擲飛鏢（每次都落在內部，且落在內部的任何一處的機會均等）。則飛鏢恰好落在陰影區域的概率為________。

答案：1.（1）4，2或3；（2）2。。

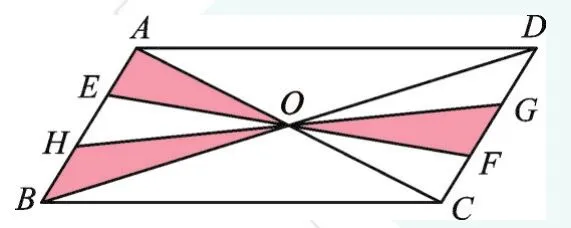
圖2