純彎狀態下高硼硅玻璃棒級聯斷裂的條件研究
王曉萌 倪俊宇 吳曠達 王盛偉 張培偉
(東南大學土木工程學院,江蘇 南京211106)
級聯斷裂這個問題最早可以追溯到理查德·費曼的意大利面試驗。在之后的幾十年的時間內,許多科學家都對此問題進行了研究但都沒有打破規律。
在2005 年,在這個問題被提出來近五十年后,兩位法國科學家Basile Audoly 和Se'bastien Neukirch 在Physics Review Letters 上發表了一篇論文。在文章中,兩位學者考慮了在面條彎曲初始斷裂后的情景[1]。
在他們發表這篇論文前幾個月,美國和法國的一個團隊就意大利面斷裂問題,在Physics Review Letters(PRL)發表了一篇論文。這個小組的視角與他們略有不同,關注的是動態沖擊而不是準靜態載荷,發現面條也是斷裂成幾截[2]。
2018 年,PNAS 上發表了一篇名為《Controlling fracture cascades through twisting and quenching》的文章,文章中通過將意大利面進行扭轉后再對其施加彎矩直至斷裂,此時,面斷成了兩截,打破了費曼的猜想[3]。
在國內也有相似的研究。其中相關度較高的是湖南大學李鳳云對于脆性梁的彎曲波傳播問題的研究[4]。
級聯斷裂是一種災難性的失效形式,目前建筑,橋梁,機械結構中為了避免此類事故的發生,往往是通過采用性能更好的材料,更夯實的結構形式,冗余度更高的結構設計段[5],人們至今對級聯斷裂的機理仍然缺乏完整的理解,也缺乏更經濟高效的解決方手段。本文以高硼硅玻璃棒為例,建立了長細桿件級聯斷裂的理論模型,利用應力波理論分析了長細桿件發生級聯斷裂的機理。
1 試驗概況
1.1 試件及其物理性質
試驗采用高硼硅玻璃棒作為試件,高硼硅玻璃棒的各項性質比較均勻,且易于發生脆性破壞,是理想的作為試件的材料。高硼硅玻璃棒的物理參數參見表1。

表1 高硼硅玻璃棒各項參數
1.2 純彎曲試驗方法
采用萬能材料試驗機進行四點彎加載,恒位移控制加載速率,加載速率為0.5mm/min,計算機自動采集數據。加載至玻璃棒發生斷裂,停止加載。
試驗采用二分法確定純彎曲段的長度,先取150mm 為純彎曲段的初始長度,然后取另一使高硼硅玻璃棒發生不同斷裂狀態(分為是否發生級聯斷裂良種化狀態)的純彎曲段長度,然后逐漸向這兩個值得中間逼近,直至區間長度小于直徑。
2 試驗結果與分析
2.1 純彎曲試驗現象
純彎曲試驗過程中,隨著荷載的增加,高硼硅玻璃棒彎曲程度增大但不明顯,無明顯裂痕,荷載增加到一定值,高硼硅玻璃棒突然斷裂。斷裂的位置大多在高硼硅玻璃棒的三等分點的中間區段,以這種形式斷裂的高硼硅玻璃棒斷裂后的碎片較多且較小,部分高硼硅玻璃棒在壓頭位置斷裂,且多斷裂為兩段。
2.2 純彎曲試驗結果
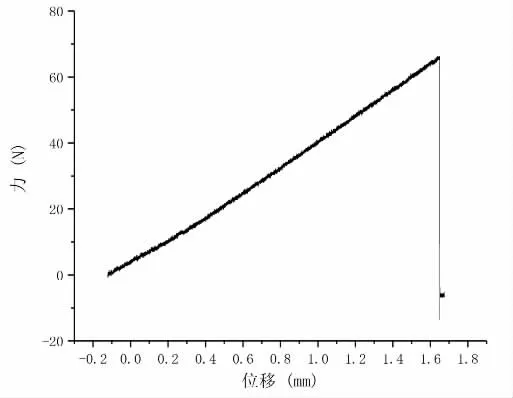
圖1 純彎狀態下高硼硅玻璃棒P-δ 曲線
由高硼硅玻璃棒的P-δ 曲線可見:高硼硅玻璃棒的P-δ曲線大致呈現一條直線,高硼硅玻璃棒在純彎狀態下始終處于彈性狀態。
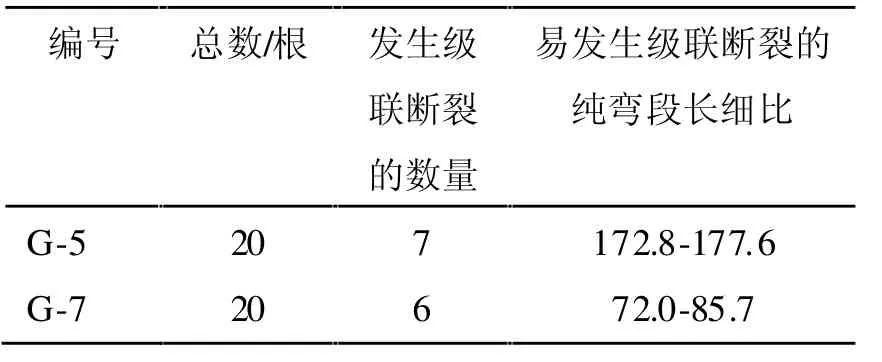
表2 高硼硅玻璃棒數據測量表
表2 是高硼硅玻璃棒發生級聯斷裂時的統計結果。高硼硅玻璃棒發生斷裂時的中點撓度,中點曲率和最大應力的各項數值(這里只列舉發生級聯斷裂的高硼硅玻璃棒)參見表3。
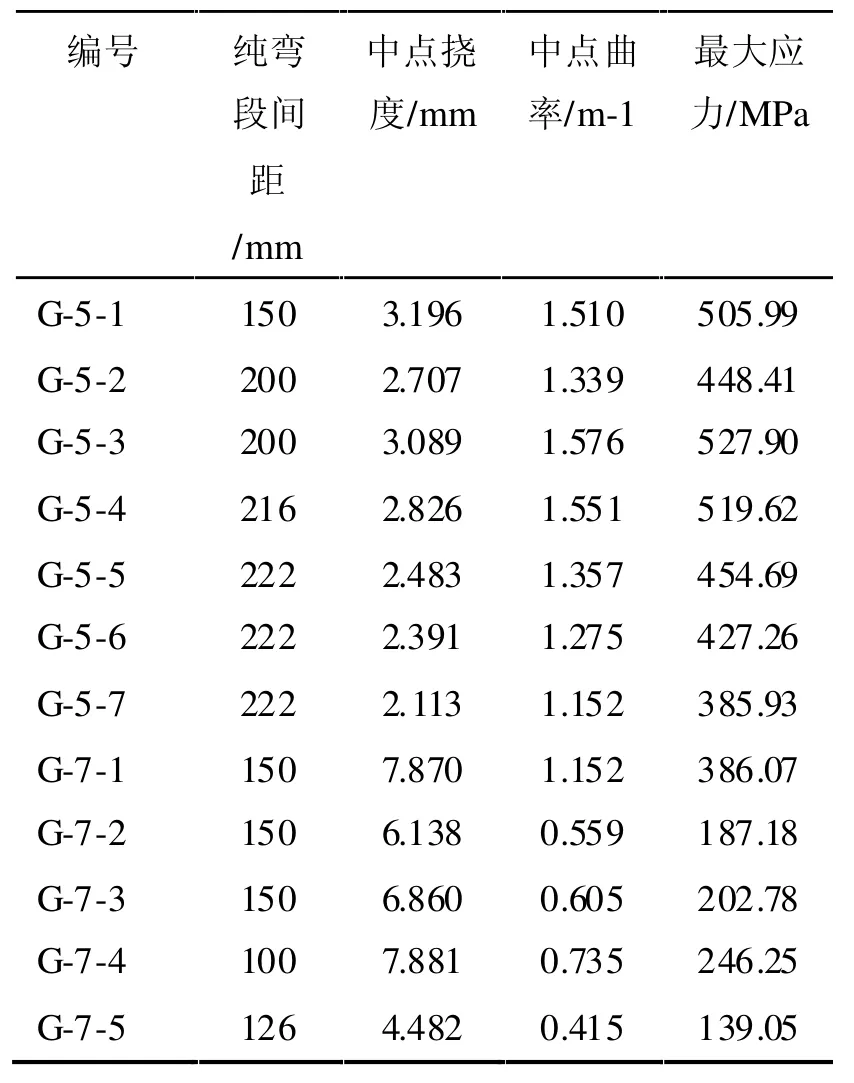
表3 高硼硅玻璃棒發生級聯斷裂時的各項數值
2.3 應力波理論分析
根據純彎曲梁的彈性力學精確解,其橫截面保持為平面,兩端簡支的玻璃棒純彎曲問題可簡化為一維問題[6]。在一維桿的縱向運動中,其連續性方程(相容方程)為:

式中:v 為桿中質點的速度,x 為用Lagrange 方法描述的物質坐標,ε 為應變。
一維桿縱向運動的動力學方程為:

式中:ρ 為桿的密度,為不隨時間與空間變化的常量,σ 為應力。
為了簡化模型,玻璃棒材料的本構關系[7]
采用:

式中:E 為玻璃棒的彈性模量,為不隨空間與時間變化的常量。
引入:

顯然,C 也是一個不隨時間與空間變化的常量。
將上式(4)與本構關系式(3)代入動力學方程(2)得到:

采用特征線法求解得特征線上相容關系:

或

可見C 表示物質波面傳播的速度。上式(7)確定了應力σ與質點速度v 之間的關系,稱ρC 為波阻抗或聲阻抗。
如果u 的一階導數間斷,也即質點速度v 和應變ε 在波陣面上有突躍,則稱為一階奇異面或強間斷,這類應力波也稱為沖擊波。
應力波根據傳播方向分為左行和右行。對于右行沖擊波,根據質量守恒條件,波陣面上的運動學相容條件為:

根據動量定理,波陣面上的動力學相容條件為:

對于左行波,其波陣面相容方程將-C 替換上式中的C 即可。
下面考慮應力波在自由邊界處上的反射。對于被施加了軸向沖擊的一維桿件,假設其左右兩端初始狀態分別為v1,ε1,σ1與v2,ε2,σ2(圖2a),分別對應圖2(f)中的1、2 兩點。之后應力波分別以波速C0 向中間傳播,當兩波相遇時,應力波發生反射,向兩端傳播。相遇點處速度、應力發生突變,設為v3、σ3。
根據波陣面上的相容條件(式9)
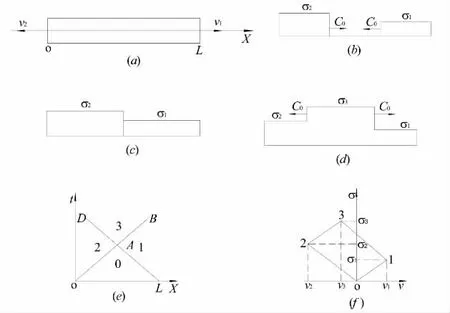
圖2 迎面傳播的兩沖擊波的相互作用
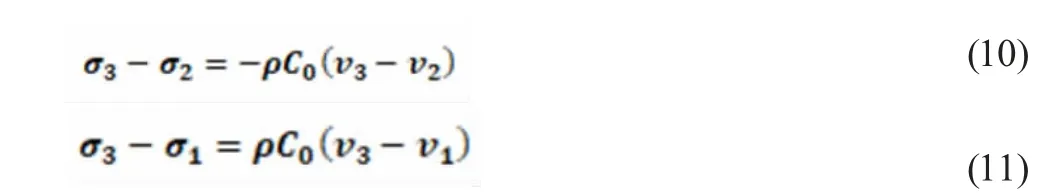
可解得σ3、v3,對應于圖2(f)中的狀態3。也可以根據疊加定理求得。
若在自由端發生反射,則

有v2=v1,v3=2v1。
另外,應力波在不同介質中發生反射與透射時,入射波擾動ΔσⅠ傳遞到界面上時,反射波擾動

式中:F 為反射系數,滿足

式中:n 為兩介質的聲阻抗之比。
純彎曲下的玻璃棒發生斷裂時,斷面的應力突然釋放,相當于在兩端施加了一個沖擊荷載,其在斷面造成的初始應力與靜態彎曲荷載下的應力的疊加為效果為0,即邊界成為自由端。隨后該沖擊荷載造成的應力波分別從兩端向中間傳播,相遇后發生反射,在自由端面再次反射后成為加載波,與靜荷載下的彎曲應力疊加,造成二次斷裂或者多次斷裂。且靜載下的應力越大,一次斷裂后,更容易發生二次或多次斷裂,即級聯斷裂。
此外,與層裂或崩落現象類似,斷裂的玻璃棒碎片會帶著傳遞的脈沖的全部動量飛出,因此碎片具有初始速度。且因為裂縫間存在一定間距,即碎片具有一定長度,其兩端的運動狀態并不一致,速度不相等,因此在飛出的過程中還會產生角速度。
從直接的實驗現象看,玻璃棒因級聯斷裂飛出的碎片的確具有初始速度,與應力波理論相符。
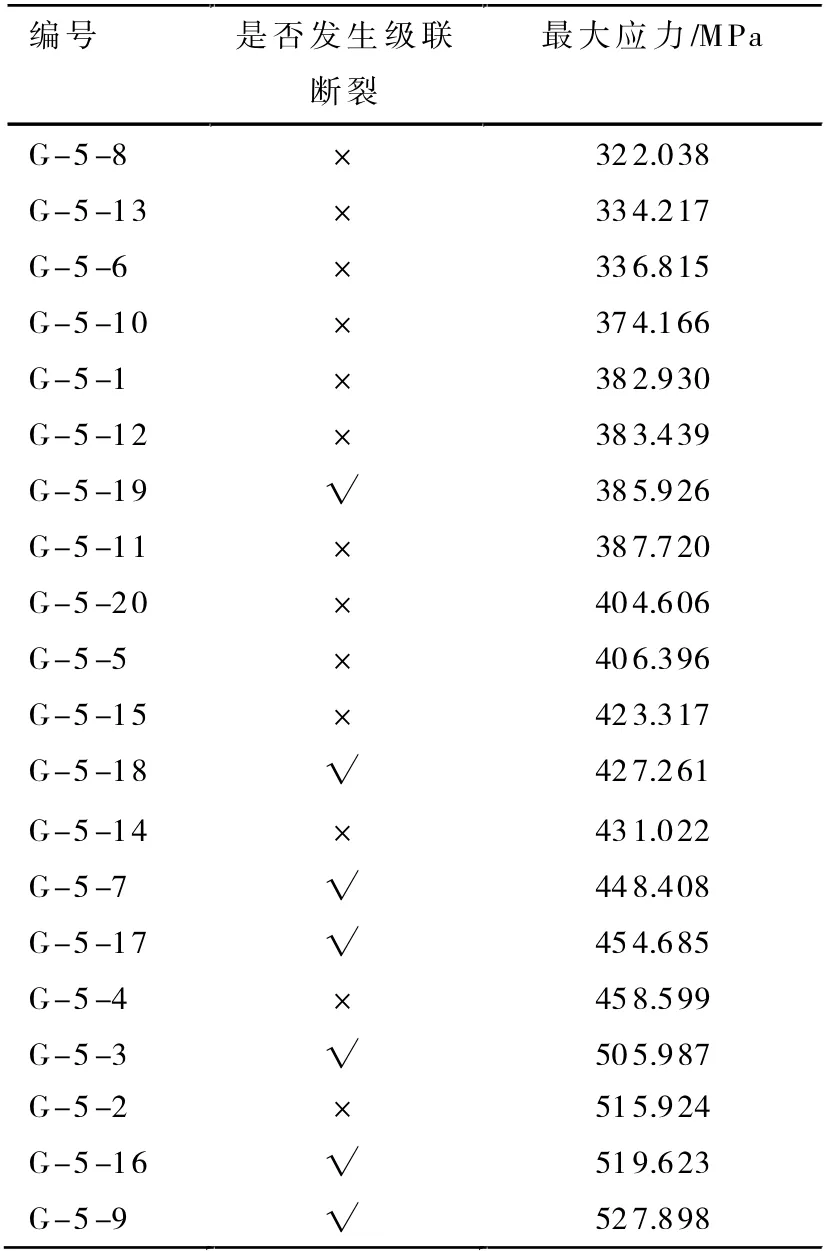
表4 直徑5mm 高硼硅玻璃棒最大應力順序排序

表5 直徑7mm 高硼硅玻璃棒最大應力順序排序
從表4、表5 可以看出,如果玻璃棒有瑕疵,則較早斷裂,不會發生級聯斷裂;如果玻璃棒品質越好,則其斷裂時的撓度越大、最大應力也越大,也更容易發生級聯斷裂,與應力波理論相符。
3 結論
本文通過對不同尺寸的高硼硅玻璃棒進行純彎曲試驗,并用應力波的相關理論對試驗的數據和現象進行分析,得到如下結論:
3.1 在純彎曲狀態下,高硼硅玻璃棒發生級聯斷裂的位置在純彎曲段的三等分點的中間區段。高硼硅玻璃棒發生級聯斷裂時需其純彎曲段曲率很大。
3.2 對于純彎曲狀態下的高硼硅玻璃棒,其中點應力達到一定值后,高硼硅玻璃棒突然斷裂,斷口處的邊界條件突然變為自由邊界,應力突變為0,相當于在兩端突然施加一個沖擊,應力σ 和速度v 突變,產生的沖擊應力波,并向另一端傳播,導致高硼硅玻璃棒發生二次斷裂,甚至多次斷裂。
3.3 猜想:桿件斷裂,由桿件斷口處產生沖擊應力波,應力波在桿件中傳播,反彈,疊加,達到桿件的承載極限,發生再一次的斷裂,斷裂一直持續直至能量不足以引發斷裂。

