基于加權(quán)余弦相似度與極限學(xué)習(xí)機(jī)的電力負(fù)荷短期預(yù)測(cè)

李海俠， 林繼燦， 李 賡， 黃致勇

(桂林理工大學(xué)機(jī)械與控制工程學(xué)院，桂林 541000)

電力負(fù)荷預(yù)測(cè)是通過(guò)對(duì)歷史數(shù)據(jù)進(jìn)行建模分析和推算，對(duì)控制電力系統(tǒng)具有深遠(yuǎn)的意義[1-2]。目前電力負(fù)荷預(yù)測(cè)方法為電力行業(yè)帶來(lái)較好的經(jīng)濟(jì)效益，因此，提高負(fù)荷預(yù)測(cè)的準(zhǔn)確性，對(duì)電網(wǎng)運(yùn)行的操作以及機(jī)組維修具有重要作用。

為提高電力負(fù)荷預(yù)測(cè)的準(zhǔn)確性，兼容于負(fù)荷變化的多樣性、周期性和有條件性，多種負(fù)荷預(yù)測(cè)方法被相繼提出，其中以人工智能算法最受關(guān)注。主要的預(yù)測(cè)方法包括人工神經(jīng)網(wǎng)絡(luò)(artificial neural network)法[3]、支持向量機(jī)(spupport vector machine,SVM)[4]、灰色模型法[5]等。文獻(xiàn)[6]采用組合灰色預(yù)測(cè)模型進(jìn)行短期電力負(fù)荷預(yù)測(cè)，該方法對(duì)預(yù)測(cè)變化要求需要指數(shù)變化，具有較低的推廣性。文獻(xiàn)[7]建立SVM電力負(fù)荷短期預(yù)測(cè)模型，對(duì)后續(xù)SVM研究有一定參考意義。

由于電力負(fù)荷預(yù)測(cè)中，影響電力負(fù)荷變化的各因素包括云量、濕度、溫度等，它們的關(guān)系是具有非線性的，因此，在預(yù)測(cè)模型建立之前進(jìn)行相關(guān)物理數(shù)據(jù)處理能有效提高預(yù)測(cè)的精確性。在電力負(fù)荷預(yù)測(cè)應(yīng)用中較為常見(jiàn)的為K聚類算法、相似日法、連續(xù)時(shí)間段聚類等。文獻(xiàn)[8]采用用戶聚類算法，篩選有效電力數(shù)據(jù)指標(biāo)，對(duì)后續(xù)聚類分析算法的改進(jìn)具有一定參考價(jià)值；文獻(xiàn)[9]采用日相似分類，利用預(yù)測(cè)日期的相關(guān)物理參數(shù)，進(jìn)行相似日的分類規(guī)劃，作為算法訓(xùn)練的輸入，建立風(fēng)電功率預(yù)測(cè)模型，有效提高了預(yù)測(cè)精度。為此，預(yù)測(cè)模型建立前對(duì)電力負(fù)荷相關(guān)物理數(shù)據(jù)進(jìn)行處理具有重要的作用。

極限學(xué)習(xí)機(jī)(extreme tearning machine,ELM)在解決非線性和高維模式識(shí)別問(wèn)題上具有較好的處理性能，在電力負(fù)荷預(yù)測(cè)中獲得較為廣泛的應(yīng)用[10]。文獻(xiàn)[11]將ELM運(yùn)用于短期負(fù)荷預(yù)測(cè)中，并獲得一定的預(yù)測(cè)效果。文獻(xiàn)[12]針對(duì)分類問(wèn)題，提出一種基于優(yōu)化方法的改進(jìn)極限學(xué)習(xí)機(jī)。因此，ELM的學(xué)習(xí)和拓展仍然具有較大的發(fā)展空間，在電力負(fù)荷應(yīng)用中，ELM同樣具有高效性。

基于以上分析，提出加權(quán)余弦相似度與ELM的支持向量機(jī)電力負(fù)荷短期預(yù)測(cè)，利用加權(quán)余弦相似度進(jìn)行數(shù)據(jù)篩選，選取相似日電力負(fù)荷輸出歷史數(shù)據(jù)作為ELM的輸入，簡(jiǎn)化運(yùn)算的輸入數(shù)據(jù)，利用某地區(qū)電力數(shù)據(jù)構(gòu)建預(yù)測(cè)模型，預(yù)測(cè)結(jié)果與SVM以及BP(back propagation)神經(jīng)網(wǎng)絡(luò)進(jìn)行比較分析，該方法能有效提高預(yù)測(cè)精度。

1 加權(quán)余弦相似度模型

在電力負(fù)荷采集的相關(guān)物理數(shù)據(jù)中，挑選與待測(cè)日相近的電力負(fù)荷輸出數(shù)據(jù)作為訓(xùn)練樣本，簡(jiǎn)化計(jì)算量。電力數(shù)據(jù)中包含濕度、日最高負(fù)荷、最低負(fù)荷、風(fēng)速等影響參數(shù)，設(shè)i個(gè)歷史日電力負(fù)荷影響參數(shù)的特征向量為Xi=[xi(1),xi(2),…,xi(m)]T，待測(cè)日為X0，m為影響參數(shù)的數(shù)量，基于相似日的思路中，歐式距離在相似點(diǎn)選取中獲得較為直觀的成果，電力負(fù)荷數(shù)據(jù)各點(diǎn)歐式距離ri的計(jì)算公式為[13]

(1)

對(duì)于文本向量，歐氏距離權(quán)重于絕對(duì)值在數(shù)值維度當(dāng)中的差異作用，而余弦相似度更關(guān)注層面的差異。在文本的電力負(fù)荷物理數(shù)據(jù)相似度篩選中，數(shù)據(jù)點(diǎn)位置在不同日期中同一個(gè)時(shí)間點(diǎn)內(nèi)是否同時(shí)出現(xiàn)，即相同維度上是否同時(shí)相近，是作為判斷相似的指標(biāo)，而對(duì)于數(shù)據(jù)點(diǎn)出現(xiàn)的次數(shù)，即相同維度上數(shù)值的差異，其相對(duì)重要作用程度減小，故此，向量夾角的余弦值在本文電力負(fù)荷處理上更能篩選出負(fù)荷向量間的關(guān)聯(lián)相似度，所以第i個(gè)樣本負(fù)荷參數(shù)與待測(cè)參數(shù)特征向量的加權(quán)余弦相似度為

(2)

為精確物理信息關(guān)聯(lián)的選取，在選取函數(shù)中加入權(quán)重，以平衡影響函數(shù)的比重。權(quán)重一般受限于專家知識(shí)、經(jīng)驗(yàn)的匱乏的影響。熵權(quán)法在權(quán)重確定上可以反映不確定信息量，具有客觀性。利用熵權(quán)法進(jìn)行電力負(fù)荷相關(guān)物理信息的權(quán)重選取。假設(shè)n個(gè)相關(guān)物理信息數(shù)據(jù)中，有m個(gè)參數(shù)，用bij表示第i個(gè)歷史日下的第j項(xiàng)物理信息值，則第j項(xiàng)指標(biāo)的第i個(gè)歷史日的比重[14]:

(3)

第j項(xiàng)指標(biāo)的熵:

(4)

如果aij為0的時(shí)候，lnaij無(wú)意義，此時(shí)修正為

(5)

則第j個(gè)物理參數(shù)的權(quán)重為

(6)

(7)

2 極限學(xué)習(xí)機(jī)

為了提高神經(jīng)網(wǎng)絡(luò)學(xué)習(xí)速度的效率，同時(shí)解決計(jì)算過(guò)程容易陷入局部極小點(diǎn)而無(wú)法獲取全局最優(yōu)解等缺點(diǎn)，Huang等[15]提出極限學(xué)習(xí)機(jī)ELM的單隱含層式前饋神經(jīng)網(wǎng)絡(luò)。ELM訓(xùn)練過(guò)程中無(wú)須調(diào)整隨機(jī)獲取的閾值，只需要一次迭代運(yùn)行就能獲得唯一的最優(yōu)解。

假設(shè)歷史日訓(xùn)練集Q={(x1,y1),…,(xi,yi)}，i=1,2，…,n，其中xi為訓(xùn)練集輸入，yi為訓(xùn)練輸出，n為訓(xùn)練個(gè)數(shù)。含有N個(gè)隱層節(jié)點(diǎn)激勵(lì)函數(shù)為G的極限學(xué)習(xí)機(jī)回歸模型可表示為[16]

(8)

式(8)中：βi為第i個(gè)隱層節(jié)點(diǎn)與輸出神經(jīng)元的連接權(quán)值；ai和bi分別為輸入神經(jīng)元與第i個(gè)隱層節(jié)點(diǎn)的輸入權(quán)值和偏置，同時(shí)在訓(xùn)練開(kāi)始隨機(jī)產(chǎn)生，無(wú)須進(jìn)行變換；h(x)=[G(a1,b1,x1),…,G(aN,bN,xN)]為隱層輸出矩陣。連接權(quán)值通過(guò)求解式(9)中的最小二乘解來(lái)獲得。

(9)

其最小二乘解為

β=H+T′

(10)

式(10)中：H+為隱含層輸出矩陣H的Moore-Penrose廣義逆；T′為網(wǎng)絡(luò)輸出T的轉(zhuǎn)置。

基于以上分析，加權(quán)余弦相似度與ELM電力負(fù)荷短期預(yù)測(cè)流程如圖1所示，回歸模型建立步驟如下。

(1)對(duì)歷史負(fù)荷數(shù)據(jù)數(shù)列按照式(6)求取數(shù)據(jù)目標(biāo)的權(quán)值，再利用式(7)進(jìn)行加權(quán)余弦相似度篩選，獲得相似度負(fù)荷數(shù)據(jù)Q。

(2)利用加權(quán)余弦相似度選取的相似度負(fù)荷數(shù)據(jù)Q={(x1,y1),…,(xi,yi)}作為ELM的訓(xùn)練集，設(shè)置激勵(lì)函數(shù)G和隱層節(jié)點(diǎn)個(gè)數(shù)N。

(3)隨機(jī)生成輸入權(quán)值ai和偏置bi，i=1，…，N。

(4)計(jì)算隱層輸出矩陣H，利用式(10)計(jì)算輸出權(quán)值β。

(5)將輸出權(quán)值代入式(8)，獲得仿真預(yù)測(cè)。

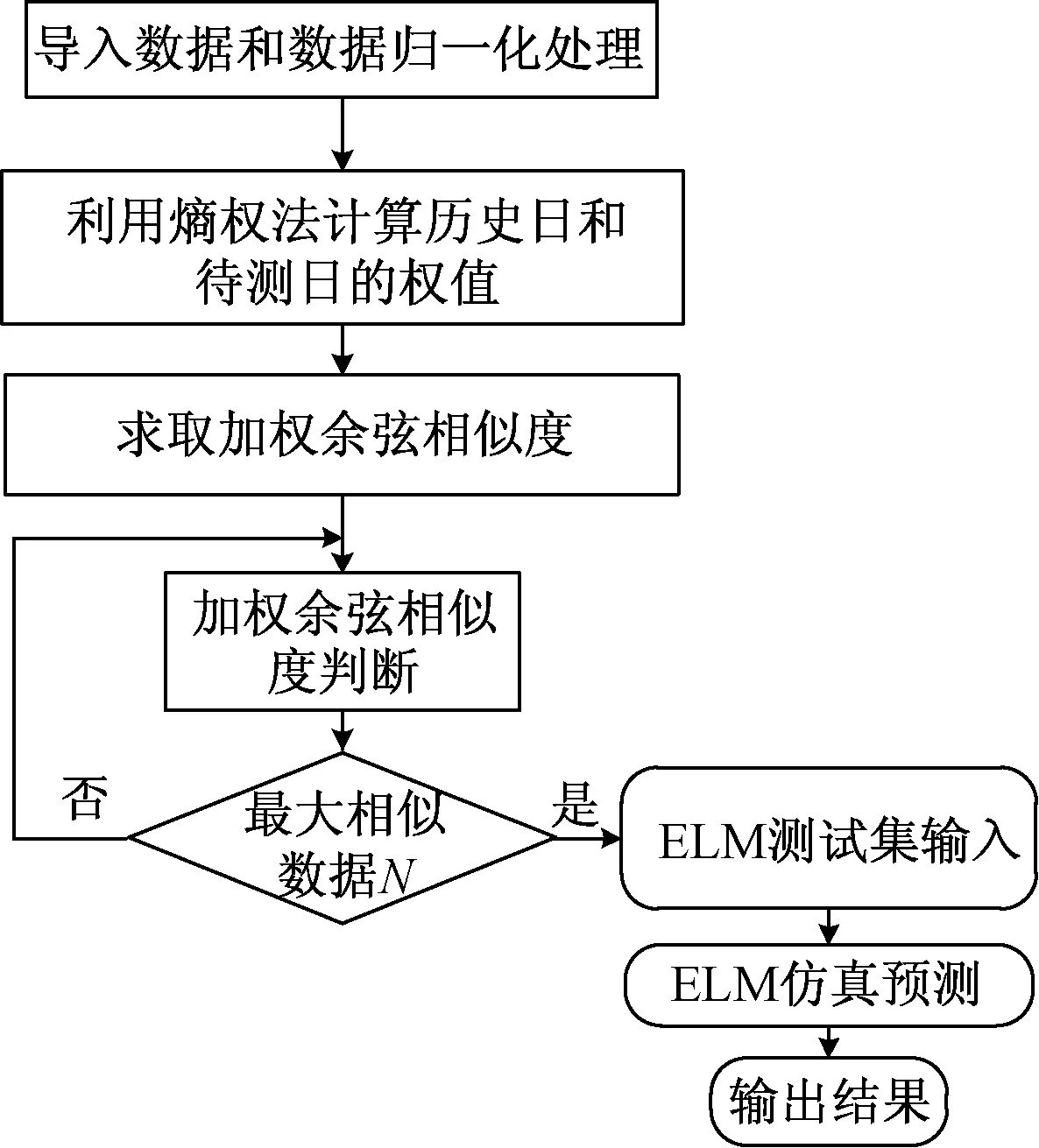
圖1 加權(quán)余弦相似度與ELM流程Fig.1 Weighted cosine similarity and ELM flow chart

3 樣例分析

為驗(yàn)證算法的有效性，利用國(guó)內(nèi)某地區(qū)年度的負(fù)荷及影響數(shù)據(jù)作為樣本。采用周期為0.5 h。選取其中50 d作為訓(xùn)練樣本驗(yàn)證算法，測(cè)試樣本為50 d樣本的后一天數(shù)據(jù)。數(shù)據(jù)讀取方式為間隔0.5 h對(duì)應(yīng)的一天數(shù)據(jù)為一列。預(yù)測(cè)效果評(píng)價(jià)指標(biāo)相對(duì)較多，選取平均絕對(duì)百分比誤差(mean absolute percent error,MAPE)和均方根誤差(root mean square error,RMSE)作為評(píng)價(jià)指標(biāo)。

(11)

(12)

式中：S為實(shí)際電力負(fù)荷；Y為電力負(fù)荷預(yù)測(cè)值。為了驗(yàn)證利用加權(quán)余弦相似度篩選出來(lái)的數(shù)據(jù)作為ELM預(yù)測(cè)輸入比直接利用歷史數(shù)據(jù)作為預(yù)測(cè)輸入效果更好，選取加權(quán)余弦相似度Fj最大的11個(gè)數(shù)據(jù)作為訓(xùn)練樣本，記本文方法為A，極限學(xué)習(xí)機(jī)電力負(fù)荷預(yù)測(cè)方法為B。預(yù)測(cè)結(jié)果對(duì)比如表1所示。

兩種方法一天電力負(fù)荷預(yù)測(cè)輸出對(duì)比如圖2所示。

表1 一天電力負(fù)荷預(yù)測(cè)結(jié)果Table 1 One-day power load forecasting results

圖2 預(yù)測(cè)輸出對(duì)比Fig.2 Predictive output contrast

分析表1和圖2，利用加權(quán)余弦相似度選取出來(lái)的數(shù)據(jù)作為ELM的輸入能有效提高預(yù)測(cè)的精度，同時(shí)減小預(yù)測(cè)誤差。圖3所示為A和B方法訓(xùn)練集的訓(xùn)練輸出對(duì)比。從圖3中能夠看出，加權(quán)余弦相似度篩選出來(lái)的數(shù)據(jù)作為ELM的輸入能夠在減小輸入的情況下保證了輸出預(yù)測(cè)的精度，可以減小系統(tǒng)的運(yùn)行時(shí)間。

圖3 訓(xùn)練集訓(xùn)練輸出Fig.3 Training output diagram of training set

在電力負(fù)荷預(yù)測(cè)中，BP神經(jīng)網(wǎng)絡(luò)受到廣泛應(yīng)用，并獲得較好的成果；GA(genetic algorithm)遺傳算法在SVM局部?jī)?yōu)化中屬于應(yīng)用較廣的一種算法。因此，為了更好地分析本文的算法，利用本文算法與BP神經(jīng)網(wǎng)絡(luò)和GA-SVM電力負(fù)荷預(yù)測(cè)對(duì)比分析。利用歷史負(fù)荷數(shù)據(jù)作為訓(xùn)練集，其中，BP神經(jīng)網(wǎng)絡(luò)中迭代次數(shù)設(shè)置為50，學(xué)習(xí)速率為0.001，訓(xùn)練目標(biāo)為10-20，GA-SVM中，遺傳算法種群規(guī)模為200，交叉率為0.4，變異率為0.01。

表2所示為評(píng)估參數(shù)對(duì)比結(jié)果，圖4和圖5所示分別為預(yù)測(cè)輸出參數(shù)對(duì)比和迭代過(guò)程結(jié)果。

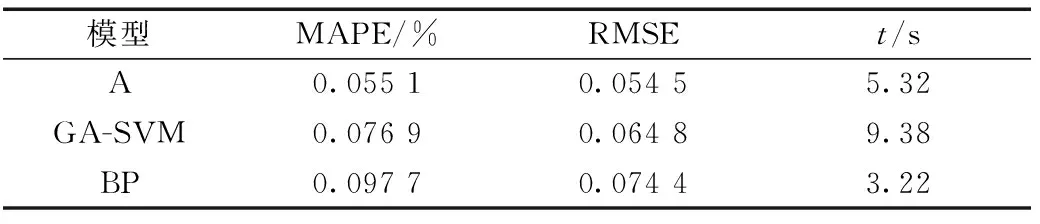
表2 多算法評(píng)估結(jié)果對(duì)比Table 2 Comparison of multi-algorithm evaluation results

圖4 多算法預(yù)測(cè)輸出對(duì)比Fig.4 Multi-algorithm predictive output contrast graph

圖5 多算法迭代效果輸出Fig.5 Multiple Algorithms Iterative Effect Output Graph

分析表2和圖4、圖5，運(yùn)算時(shí)間最短為BP神經(jīng)網(wǎng)絡(luò)，迭代次數(shù)18次就完成精確度的要求，但是預(yù)測(cè)效果為3種算法中最差的，本文提出的算法在運(yùn)算時(shí)間比GA-SVM用時(shí)更短，而且迭代次數(shù)1次內(nèi)就能完成，GA-SVM則需要100次迭代。SVM中核函數(shù)參數(shù)和懲罰因子的求解對(duì)系統(tǒng)預(yù)測(cè)產(chǎn)生較大的影響。為此3種算法中，本文提出的算法對(duì)于文本的預(yù)測(cè)為最佳。

4 結(jié)論

提出了一種基于加權(quán)余弦相似度與極限學(xué)習(xí)機(jī)ELM的電力負(fù)荷短期預(yù)測(cè)方法。該方法根據(jù)電力負(fù)荷相關(guān)物理信息的關(guān)聯(lián)性，利用熵權(quán)法求出對(duì)應(yīng)權(quán)值，賦予余弦相似度來(lái)篩選訓(xùn)練樣本，以減小ELM的輸入，從而有效縮短算法運(yùn)行時(shí)間。同時(shí)，極限學(xué)習(xí)機(jī)能有效改善BP神經(jīng)網(wǎng)絡(luò)和支持向量機(jī)中需要多次迭代達(dá)到修正而耗時(shí)過(guò)長(zhǎng)的缺點(diǎn)，具有較好的學(xué)習(xí)速率和泛化性能。最終利用實(shí)驗(yàn)驗(yàn)證了算法的有效性，同時(shí)具有更好的推廣性和一定的參考價(jià)值。