機械絮凝池內部流場特性的數值模擬研究
舒 在
(合肥工業大學 土木與水利工程學院,安徽 合肥 230009)
0 引 言
絮凝是水處理工藝中的重要一環,絮凝效果的好壞主要由兩個因素決定:一是絮凝劑的性質;其次是水處理構筑物所提供的水力學條件[1]。其中水力學條件對絮體的成長起決定性作用,是決定絮凝效率的關鍵[2]。因此,對絮凝池進行合理的設計,探討出最佳絮凝水力學條件顯得十分重要。機械絮凝是絮凝的重要組成部分,相比于水力絮凝,對其研究較少,目前對機械絮凝主要通過試驗和數值模擬來研究。包雨云等[3]研究不同葉輪直徑對方形槽中機械絮凝的影響,結果表明適當對攪拌漿直徑進行增大,可提高絮凝效果。NO-sukpark等[4]進行了燒杯模型試驗、CFD模擬,以剩余濁度和G值為絮凝效果評價指標,研究方形、圓形、帶有擋板的圓形三種不同燒杯裝置的絮凝效果,研究結果表明,帶有擋板的圓形燒杯裝置絮凝效果最好。熊水應等[5]對不同樣式攪拌器的機械絮凝池中在水廠中的運行性能進行測試比較,發現水翼式的絮凝效果更優。陳衛等[6]基于CFD模擬水流流態,通過研究兩種水力學因素對絮凝效果的影響,即攪拌器的幾何尺寸和在容器中的高度,提出了相應的合理工況。鄢碧鵬等[7]基于CFD對不同槳葉速度組合的機械絮凝池內的流場進行了數值模擬,得到了最佳絮凝效果時的速度組合。
這些對機械絮凝反應器的研究都從改變絮凝水力學條件出發,進而強化絮凝工藝過程,且都是對垂直軸式機械絮凝反應器的研究。在實際工程中,機械絮凝池的進水方式、攪拌器旋轉方向、各級反應格間過水孔洞形狀的改變都會對絮凝水力學條件產生影響,但相關設計規范對這些沒有規定,目前都是依據設計者的經驗進行設計,難免會產生一定的誤差,而這些條件對絮凝效果的影響在現有的研究中還比較少見。采用CFD數值模擬的方法可以對實際尺寸的池體內流動場進行計算,相比試驗研究而言具有更快速、更準確、費用更低等優點。因此,筆者選擇水平軸式機械池為數值模擬研究對象,研究不同進水方式、攪拌器旋轉方向、過水孔洞形狀對絮凝水力條件的影響,這對實際工程中絮凝池的設計與運行有一定的指導意義。
1 模型的建立
1.1 幾何模型的建立
數值模擬中采用三維實體模型來研究,根據《給水排水設計手冊——城鎮給水》設計要點及規范要求,單個絮凝池的設計流量為3 000 m3/d,進水直徑為800 mm,進口流速為0.69 m/s,絮凝時間為20 min,池體長度14 m,池體寬度83 m,池內設3排攪拌器,每排攪拌器上設3個攪拌器,攪拌器上的葉輪呈十字形安裝,葉輪直徑為3.3 m,十字葉輪上安裝4塊槳板,槳板長度為25 m,槳板寬度0.2 m。絮凝池分為3個相同的反應格,第一反應格內攪拌器上槳板中心點的線速度為0.5 m/s,第二反應格內的的槳板中心點線速度為0.35m/s,第三反應格內的槳板中心點線速度為0.2m/s,各排攪拌器之間用隔墻分開以防止水流短路,隔墻上下交錯開孔。圖1為底部進水的水平軸式機械絮凝池模型。
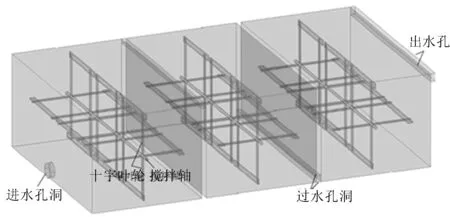
圖1 水平軸式機械絮凝池模型
1.2 數學模型的建立
機械攪拌裝置的數值模擬和實驗研究表明,對于機械攪拌的三維模擬,采用標準k-ε湍流模型較為合適,其結果與試驗數據吻合較好[8,9],因此水平軸式機械絮凝池數值模擬的基本控制方程由k方程、ε方程、連續方程、動量守恒方程組成。
2 邊界條件及模擬方法
2.1 網格劃分
利用Gambit劃分網格,網格單元類型選擇Tet/Hybrid的非結構化網格,主要為四面體。對于含有攪拌模型的處理采用多重參考系法(MRF)[10],將單個反應格分為含槳板的旋轉區域和槳板以外的靜止區域。由于含有攪拌器的旋轉區域水流流場變化劇烈,為了保證計算的精度需要對旋轉區域的網格進行加密處理,網格節點間距取60。對于靜止區域,網格節點間距取80。
2.2 邊界條件及求解器
機械絮凝池進口邊界條件為速度進口,出口邊界條件設為自由出流;近壁區域的處理采用標準壁面函數法[11],攪拌器和攪拌軸的壁面設為移動壁面,其他壁面采用固定壁面邊界條件,旋轉區域和靜止區域的分界面設為interface,自由液面設置為無剪切的對稱邊界條件。選用標準的k-ε湍流模型,采用SIMPLE算法求解。
3 模擬結果與分析
3.1 絮凝效果評價指標
湍動能k越大,湍動強度越大,水流湍動程度越劇烈,膠體顆粒間接觸碰撞概率增大,越有利于絮凝體的形成,絮凝效果也就越佳。湍動能耗散率ε表征流體將湍動能轉化為分子熱運動動能的速率,ε值越大,流體分子獲得的動能越大,絮凝顆粒間碰撞越為頻繁,絮凝效果越好,ε是有效能耗,是對顆粒碰撞起作用的那部分能量。渦旋速度梯度G與ε有關,ε越大,G越大,絮凝顆粒有效碰撞頻率越高,絮凝效果越好。在傳統絮凝池設計中,主要用速度梯度G進行校核,但是近年來許多學者對此提出異議,認為G值僅代表能量的空間平均分布,不能反映各局部能量的分布[12,13],渦旋速度梯度G是速度梯度G的一部分,在紊流情況下,G起主導作用,能反映出絮凝區內部局區域的紊動情況。因此,選用湍動能、湍動能耗散率、渦旋速度梯度為絮凝效果的評價指標。
3.2 模擬方法可行性驗證
在實際水處理絮凝過程中G值范圍一般為20~70s-1,平均GT值范圍為104~105。速度梯度G值和渦旋速度梯度G值計算式如下:
G=102×NμW
(1)
G0=ρεμ
(2)
式中:N為葉輪所耗總功率,kW;μ為水的動力黏度,水溫按20 ℃計,μ=102×10-6kg·s/m2;W為絮凝池的有效容積,m3;ρ為水的密度,1 000 kg/m3;ε為湍動能耗散率,m2/s3。
以底部進水、攪拌器順時針旋轉的水平軸式機械絮凝池為例,由槳板尺寸及轉速計算得到整個池體的平均速度梯度G為37 s-1,通過數值模擬所得到的池體平均渦旋速度梯度G0為36.53 s-1,兩者比較接近。
根據模擬結果,截取Y-Z(X=0 m)截面作為分析截面,其速度云圖和跡線圖如圖2所示。
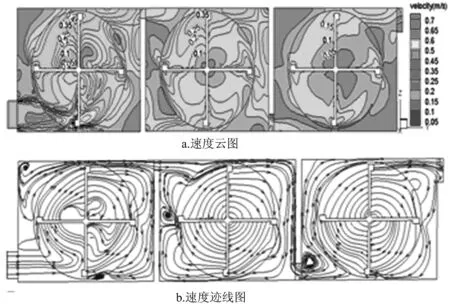
圖2 Y-Z(X=0)處截面速度云圖與跡線圖
機械絮凝池中的水流湍動主要是靠槳板的旋轉驅動水流而形成的,由圖2a可以看出第一反應格內水流的流速最高,第三格最小,從槳板外緣到靠近攪拌軸方向速度逐漸減小,且3個反應格中槳板中心線速度與設計的槳板中心線速度基本相符。由圖2b可以看出,在槳板作用下,水是順時針流動的,當撞擊到側壁上時,水流方向發生了變化,模擬所得到的絮凝池內的水流流態與實際是相符的。因此,絮凝池模型是可靠的,數值模擬中參數的設置是可行的。
3.3 不同進水方式及攪拌器旋轉方向的模擬
利用機械絮凝池不同的進水方式和攪拌器的旋轉方向,可以得到4種不同的模擬方案。不同方案的具體設計見表1所示。

表1不同方案參數設計要求
根據不同方案的模擬結果,可得到不同池體內的湍動能k分布云圖,為便于研究整個池體內部流場流態,取葉輪槳板中心點所在的平面為分析截面,不同方案的湍動能分布云圖如圖3所示。

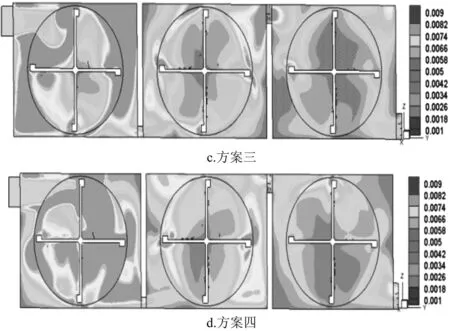
圖3 不同設計方案下湍動能分布云圖
由圖3可知,機械絮凝池內部湍動能在攪拌器附近比其他區域要高,特別是在槳板最外緣高區域較多,攪拌器所在區域使得整個反應格紊動加劇,并且這種加劇程度隨著攪拌器轉速的減小而降低。
由不同方案下機械絮凝池各個反應格的體平均湍動能k和體平均湍動能耗散率ε的模擬結果可以看出機械絮凝池內部紊動情況,具體數據見表2~表5。
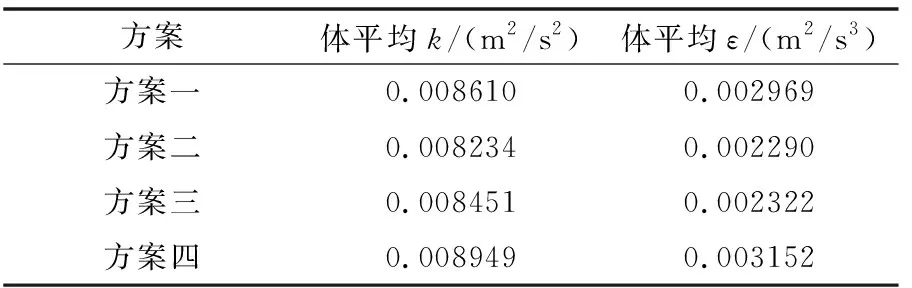
表2 不同方案下第一反應格體平均湍動能k和體平均湍動能耗散率ε
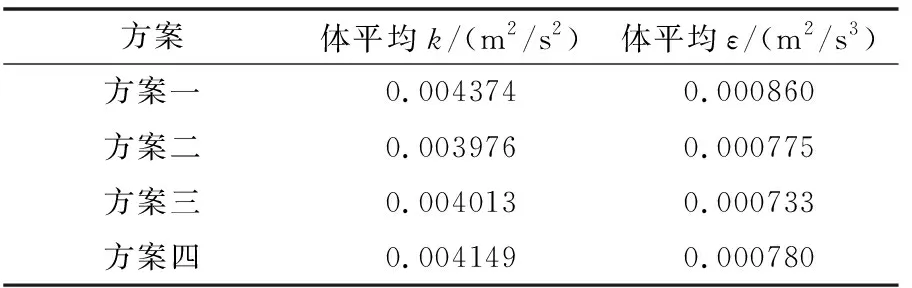
表3 不同方案下第二反應格體平均湍動能k和體平均湍動能耗散率ε
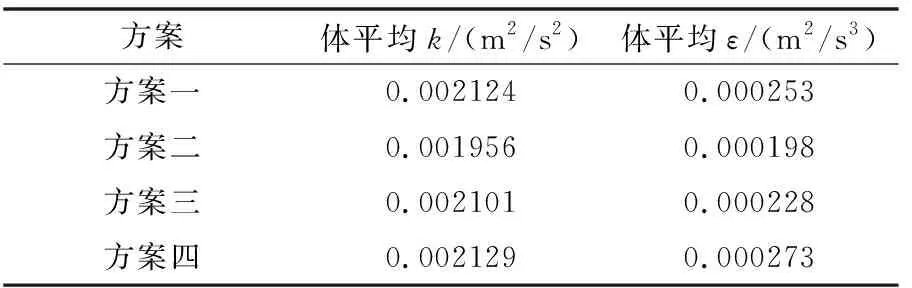
表4 不同方案下第三反應格體平均湍動能k和體平均湍動能耗散率ε
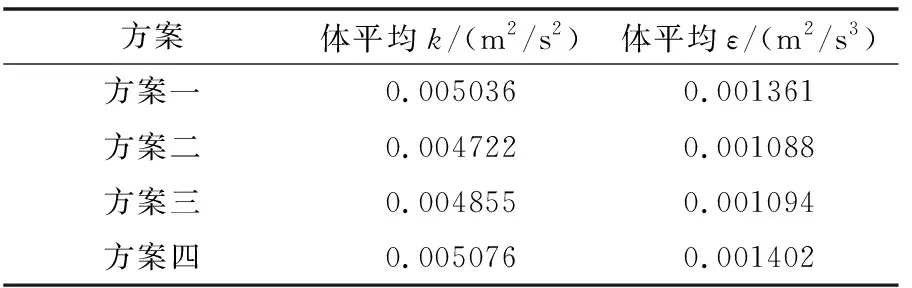
表5 不同方案下機械絮凝池體平均湍動能k和體平均湍動能耗散率ε
由表2~表5可知:
(1)當進水方式同為底部進水,攪拌器順時針旋轉時,水平軸式機械絮凝池各個反應格的體平均湍動能k和湍動能耗散率ε值都比逆時針旋轉相對應反應格的值要高,并且這種差異在第一反應格表現明顯;當進水方式同為上部進水,攪拌器逆時針旋轉的各個反應格體平均湍動能k和湍動能耗散率ε值比順時針相對應反應格的值要高,同樣在第一反應格差異表現明顯。這說明了攪拌器旋轉方向的改變對絮凝水力學條件的影響較大,且當改變進水方式時,最利于絮凝過程發生的攪拌器旋轉方向也發生改變。
(2)當攪拌器旋轉方向同為順時針時,底部進水的機械絮凝池各個反應格都比上部進水的機械絮凝池相對應反應格的湍動能k和湍動能耗散率ε值要高,且差異在第一反應格表現明顯;當攪拌器旋轉方向同為逆時針時,上部進水的機械絮凝池各個反應格的體平均湍動能k和湍動能耗散率ε值比底部進水的機械絮凝池相對應的反應格的值要高,且差異在第一反應格表現明顯。這說明進水方式的改變對絮凝水力學條件的影響較大,攪拌器旋轉方向改變時對應絮凝效果最好的進水方式發生改變。
綜合四種方案模擬所得的體平均湍動能k和體平均湍動能耗散率ε值進行分析,方案四即采用上部孔洞進水、攪拌器逆時針旋轉的水平軸式機械絮凝池第一反應格體平均湍動能k和體平均湍動能耗散率ε值比其他方案要高出許多,在絮凝的初始階段,絮凝顆粒能發生快速有效的碰撞凝聚成密實的絮凝體,第二、三反應格體平均湍動能k和體平均湍動能耗散率ε值與其他方案相比相差不大,且從整個池體的體平均湍動能k和體平均湍動能耗散率ε值來看,方案四的最高,絮凝效果最好。
由體平均湍動能耗散率ε值計算出渦旋速度梯度G,4種絮凝池設計方案所對應的渦旋速度梯度如圖4所示。
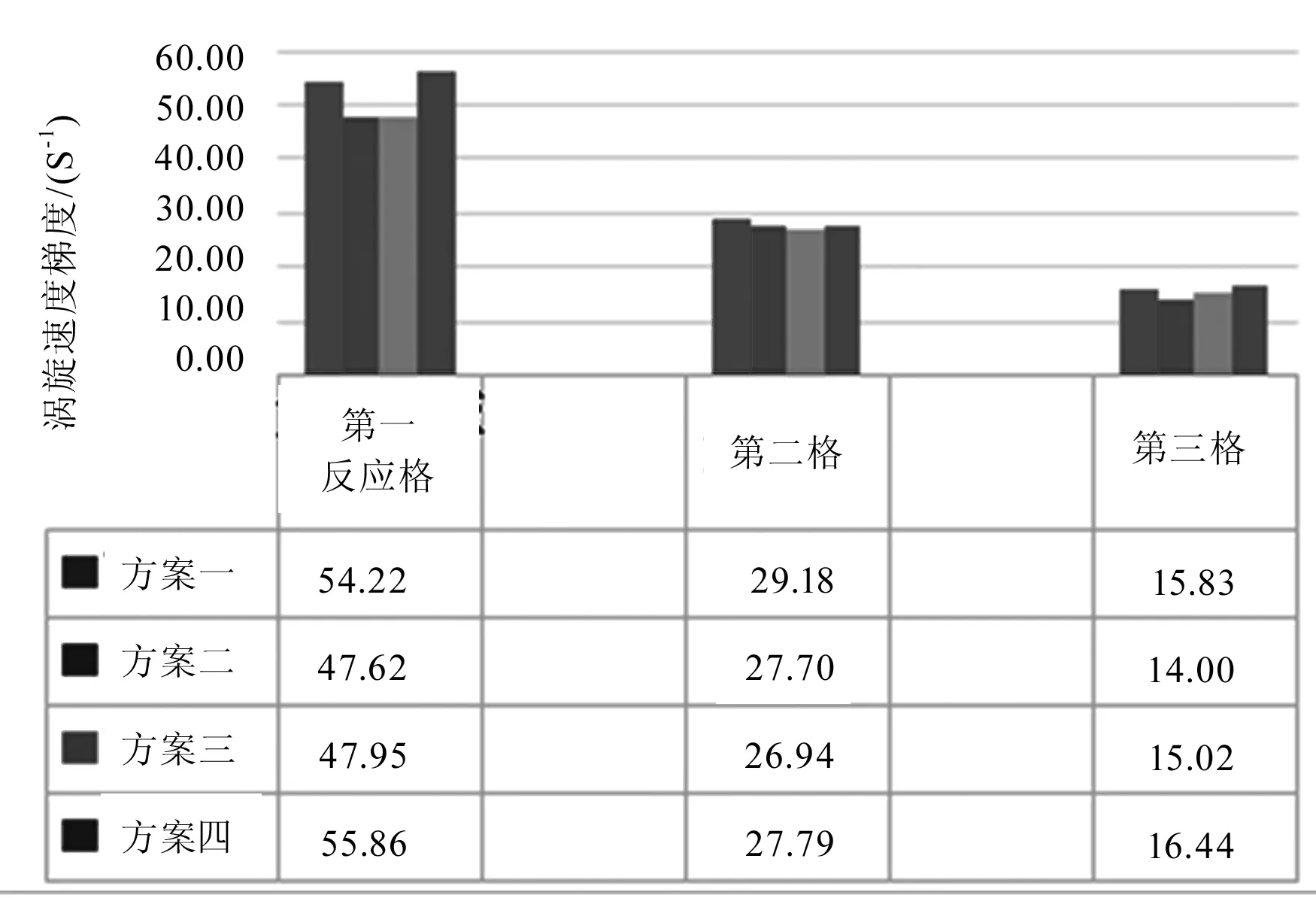
圖4 不同方案下各反應格渦旋速度梯度
由圖4可知,每種方案下,三格反應池的體平均G相差程度逐級下降,這是因為機械絮凝池水流的紊動主要是靠攪拌器的旋轉造成,攪拌器轉速越大,速度梯度越大,紊動越強,絮凝顆粒碰撞頻率越高。方案四中第一反應格體平均渦旋速度梯度達到最大55.86 s-1,第二反應格相對較高,第三反應格與其他方案相差不大,在機械絮凝過程中,第一反應格速度梯度在合理范圍內越大,則紊動越強,絮凝顆粒碰撞頻率也就越大,更有利于后續反應格絮凝反應的進行,絮凝效果也就越好,從整個池體的體平均渦旋速度梯度來看,4種方案所對應的體平均渦旋速度梯度依次為36.70 s-1、32.82 s-1、32.91 s-1、37.70 s-1,方案四最高。因此,采用上部孔洞進水、攪拌器逆時針旋轉形式的水平軸式機械絮凝池絮凝水力學條件最好,絮凝效果最佳。
3.4 不同過水孔洞形狀的模擬
基于3.3所得到的結論,對上部孔洞進水、攪拌器逆時針旋轉的機械絮凝池反應格之間過水孔洞的形狀進行數值模擬研究,3.3中機械絮凝池模型中過水孔洞為長方形孔道,寬為池寬,在控制孔洞面積及孔洞中心位置不變的情況下,對孔洞形狀為正方形及圓形的水平軸式機械絮凝池孔進行數值模擬,得出湍動能k和湍動能耗散率ε值,模擬數據見表6、表7。
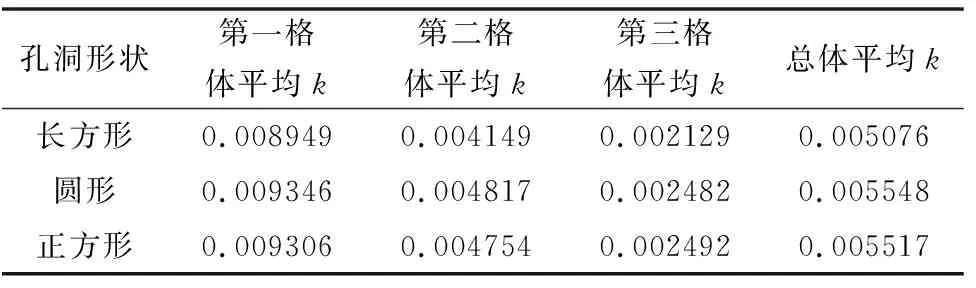
表6 不同形狀孔洞機械絮凝池體平均湍動能k(單位:m2/s2)
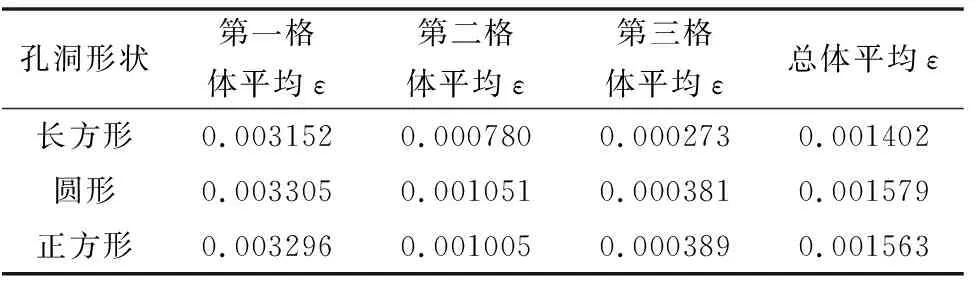
表7 不同形狀孔洞機械絮凝池體平均湍動能耗散率ε(單位:m2/s3)
在機械絮凝過程中,第一反應格應快速高效地發生碰撞凝結成粗而密實的絮凝體,第一反應格湍動越強,則絮凝效果越好;第二反應格應保持一定的湍動程度使得在第一反應格內沒有充分接觸的絮凝顆粒再次發生碰撞聚集,同時還可以將未完全壓實的大絮凝體打碎,使其重新發生碰撞,以形成致密的絮凝體;在第三反應格內水體應保持較小的湍動強度,防止已形成的絮凝體因湍流剪切過大而破碎形成小體積的礬花,由表6、表7可知,圓形孔洞的機械絮凝池第一、第二反應格體平均湍動能和體平均湍動能耗散率比另兩種形狀孔洞的要高,三種池體的第三格體平均湍動能和體平均湍動能耗散率相差不大,且從整個池體的體平均湍動能和體平均湍動能耗散率來看,圓形孔洞的最高,由湍動能耗散率算得長方形、圓形、正方形過水孔洞的機械絮凝池渦旋速度梯度分別為37.07 s-1、39.35 s-1、39.15 s-1,可知圓形孔洞的渦旋速度梯度最大。由湍動能、湍動能耗散率、渦旋速度梯度作為絮凝效果評價指標可知對于上部孔洞進水、攪拌器逆時針旋轉的水平軸式機械絮凝池,連接各反應格隔墻上的過水孔洞形狀為圓形時,絮凝效果最好。
4 結 論
本文研究了不同進水方式及攪拌器旋轉方向對水平軸式機械絮凝池絮凝水力學條件的影響,結果表明,進水方式為底部孔洞進水時,對應最佳絮凝水力條件的攪拌器旋轉方向為順時針,反之亦然,即攪拌器旋轉方向為順時針時,采用底部孔洞進水的方式絮凝水力條件最佳;進水方式發生改變時,對應最佳絮凝效果的攪拌器旋轉方向發生改變,反之亦然;4種不同進水方式及攪拌器旋轉方向的機械絮凝池的模擬結果表明采用上部孔洞進水、攪拌器逆時針旋轉的機械絮凝池絮凝效果最好;在進水方式為上部孔洞進水、攪拌器旋轉方向為逆時針的基礎上,通過對3種不同過水孔洞形狀的模擬,結果表明圓形過水孔洞的絮凝水力條件最好。
機械絮凝池中絮凝主要依靠改變攪拌器的旋轉方向、提高轉速來改善絮凝,因此結構及運行方式的優化設計顯得尤為重要。現行的相關設計規范中對水平軸式機械絮凝池的進水方式、攪拌器旋轉方向、過水孔洞形狀沒有規定,主要基于設計者的經驗,容易造成設計的隨機性,在實際工程中不能提高絮凝效果。本研究為機械絮凝池的優化設計提供了一定的理論依據,對實際工程的應用有一定的指導意義。

