社交網絡影響的不良信息擴散建模及最優控制策略

馮麗萍，韓 琦，周志剛，白增亮

（1. 山西財經大學信息學院，太原030006； 2. 忻州師范學院計算機系，山西忻州034000；3. 中北大學信息與通信工程學院，太原030051； 4. 重慶科技學院電氣與信息工程學院，重慶401331）

（*通信作者電子郵箱fenglp@yeah.net）

0 引言

在網絡信息時代，網絡空間安全已經成為從國家、組織機構到個人全民關心的一個重大問題。網絡空間安全包括網絡中信息的內容安全、傳播安全、管理安全等［1-2］。社交網絡作為目前流行的社交平臺，已經作為人們日常工作、生活、學習等活動的重要媒介。尤其是移動終端的普及，極大地提高了微信、QQ、微博等社交軟件使用的時空頻率與效率。與此同時，一些不良信息也會非常容易地通過社交網絡快速傳播，不良信息的大量傳播不僅會使網絡安全管理需要更大的經濟投入，也會影響人們的思想價值取向，對社會安全和穩定造成極大困擾。本文即是從現實需求的角度出發，利用非線性動力學和控制學理論探究網絡空間中的傳播安全問題。

自從1991年Kephart等［3-4］把人類疾病流行病模型引入計算機病毒研究，非線性動力學模型在刻畫網絡病毒及網絡不良信息傳播的研究中一直發揮著重要的作用［5-7］。但是傳統的傳播模型大都假設影響網絡中節點狀態轉換的參數為常數［8-10］，事實上，在實際網絡管理中，這些參數是根據網絡當前狀態以及各個時段組織機構對網絡安全投入的多少等因素變化的［11］。有少量文章考慮了這種現實情況，建立了控制策略的強度隨時間變化情況下，網絡中惡意軟件傳播控制模型［12-14］；但是，這些模型只針對同構網絡中惡意軟件傳播情況，沒有考慮社交網絡特性。文獻［15］研究了社交網絡影響的網絡病毒傳播控制模型和相應的控制策略，可是，該模型假設管理員采取的控制策略強度是不變的。文獻［16］基于SIR（Susceptible Infected Recovered）模型對微博信息傳播規律進行了仿真分析，沒有從理論分析的角度提出最優控制措施。鑒于以上情況，本文構建一個新的社交網絡相關的不良信息傳播模型，并基于控制理論提出控制不良信息傳播的最優控制策略。

1 模型建立

本文模型建立的基本思想是:同一社交網絡中節點之間會相互感染，不同社交網絡中節點之間也可能會間接感染。以目前流行的微信社交網絡為例，假設用戶a（a=1，2，…，m）存在某個微信群i（i=1，2，…，n）中，用戶b（b=1，2，…，m）存在某個微信群j（j=1，2，…，n）中，如果用戶a和用戶b是微信朋友關系，那么用戶a發送的不良信息既可能直接感染微信群i中的所有成員，也可能通過用戶b間接感染微信群j中的所有成員。社交網絡中節點之間的相互聯系可以通過全聯通無向圖1來表示，圖1中無向圖（a）、（b）、…、（n）分別表示不同的社交網絡群，無向圖中節點Cnk表示第n個社交網絡中的第k（k=1，2，…，m）個節點用戶，邊表示節點之間會直接相互感染，當兩個節點之間的邊數大于1時，表示這兩個節點會間接感染。

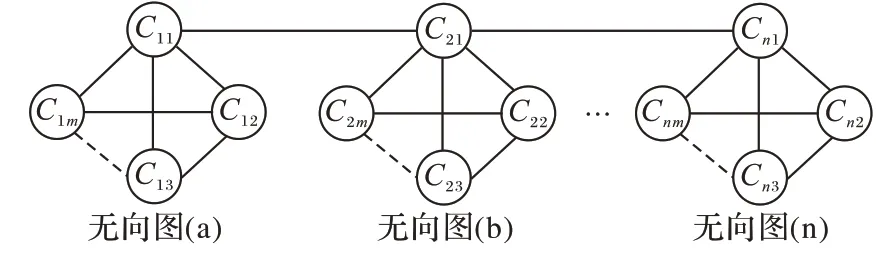
圖1 用戶社交網絡結構Fig.1 User social network structure

根據流行病建模原理［17］，假設每個社交網絡中的節點用戶分為3種狀態，分別為:易感染狀態（Susceptible，S）、已感染狀態（Infected，I）和免疫狀態（Recovered，R）。處于S 狀態的節點表示對應的用戶缺乏安全意識，容易打開一些來源不明的信息鏈接；處于I 狀態的節點表示對應的用戶會傳播不良信息或不良信息的鏈接；處于R 狀態的節點表示對應的用戶安全意識高，不會輕易打開來源不明的不安全鏈接。為了清晰，表1列出模型中用到的符號及其對應的物理含義。

表1 模型符號及其物理含義Tab. 1 Model symbols and their physical meanings

根據以上描述，建立相應的微分方程動力學模型，用式（1）表示:

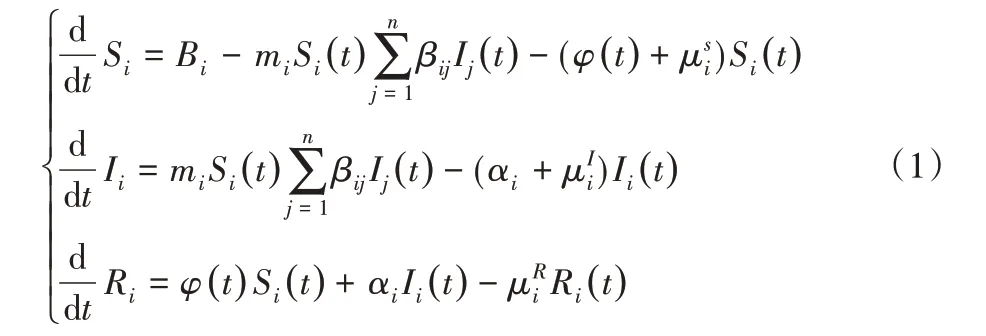
其中:φ(t)的值會隨著社交網絡中用戶的網絡安全意識、管理員的信息安全管理強度以及當下網絡安全形勢等因素而變化。當社交網絡個數n為1，φ(t)的值為常數時，模型（1）即成為文獻［16］所反映的傳統的不考慮社交網絡相互感染情況的網絡病毒傳播模型。

2 最優控制策略求解

本章的目標是找到一個控制函數滿足如下兩個條件:1）任意一個社交網絡中的已感染數達到最小值（意味著不良信息擴散的范圍達到最小）；2）實施控制策略所需的投資最少。為此，式（1）中控制函數的優化問題可以用求解式（2）的最小值表示:

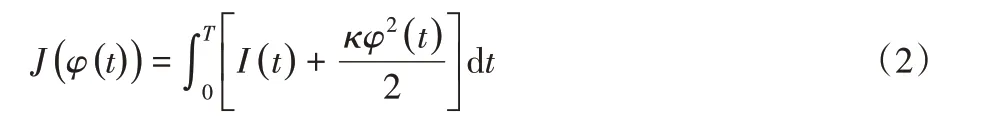
其中κ是調節因子。

顯然，式（1）和式（2）的優化控制問題，有拉格朗日方程:

為了得到式（3）的最小值，需要求解φ(t)，為此，定義相應的哈密頓方程如式（4）:

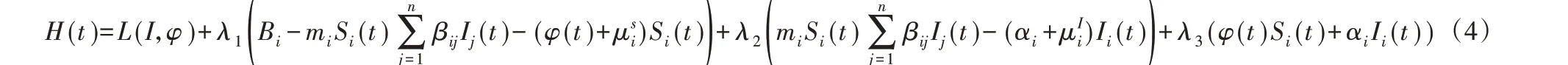
證明 容易驗證:1）式（1）的控制變量和狀態變量都大于等于0；2）集合φ是閉區間上的凸集；3）式（1）右邊是與狀態變量相關的線性時變系統；4）L(I，φ)是關于有界區域φ的凸函數；5）存在一個常量?＞1，和兩個正數ζ1和ζ2滿足L(I，φ) ≥ζ1+ζ2(|φ|)?/2。根據文獻［18］的結論，定理1得證。

式（5）需滿足邊界條件:λij（T）=0（j= 1，2，3），而且優化控制變量φ*（t）由式（6）給定:

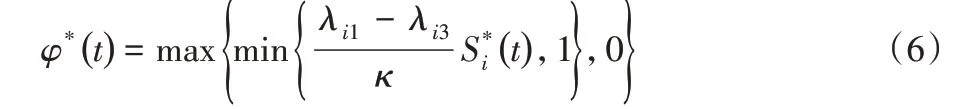
證明 對式（4）各狀態變量求導，并結合λij的含義，得:

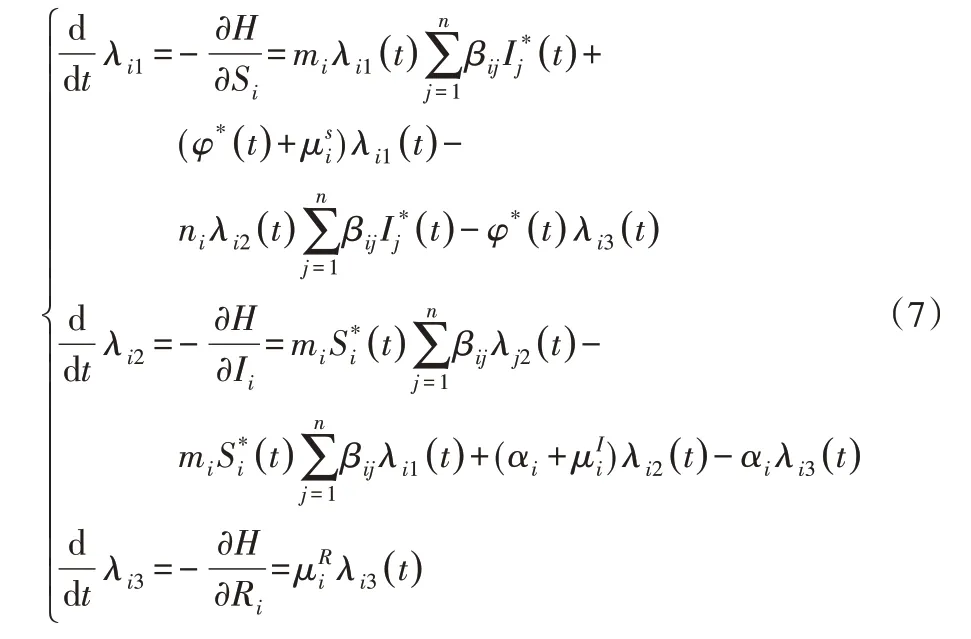
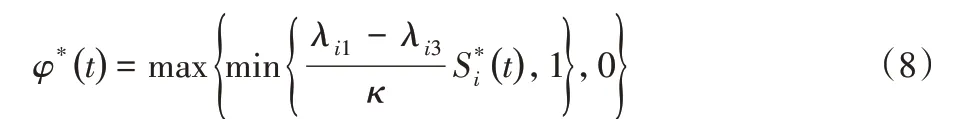
定理得證。

把式（8）代入式（1），得優化系統式（9）:

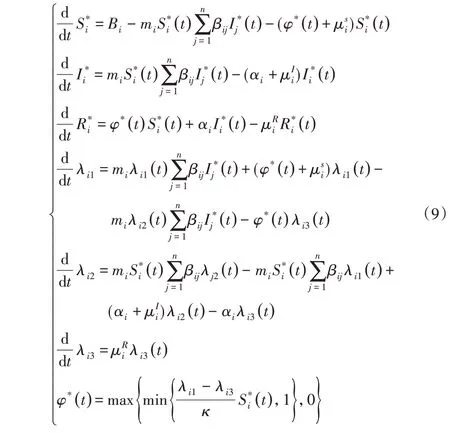
3 實驗仿真

為了觀察微分方程（1）和（9）反映的不良信息的擴散過程，本章采用龍格-庫塔（Runge-Kutta）法對微分方程（1）和優化系統（9）進行數值求解，在Matlab 2016R 環境下進行仿真驗證。模型（1）和（9）中的參數分為兩種類型:系統參數（Bi和μi）和狀態轉換參數（除系統參數之外的其余參數），其中系統參數反映社交網絡中用戶的流動速率，狀態轉換參數反映社交網絡用戶行為以及控制措施對不良信息擴散的影響程度。另外，系統的初始狀態，即Si(0)，Ii(0)和Ri(0)對社交網絡間不良信息的擴散也會產生很大影響。不失一般性，實驗時假設Ii(0)和Ri(0)的取值較小。仿真實驗主要是:1）比較引入控制策略和不引入控制策略兩種情況，社交網絡間不良信息的擴散過程；2）比較變化的控制策略和固定控制策略對不良信息擴散影響的不同；3）對比有交叉感染和沒有交叉感染兩種情況下不良信息擴散過程。

1）首先，比較模型引入優化控制策略和不引入控制策略時不良信息擴散的結果，也就是對式（1）和式（9）刻畫的不良信息擴散過程進行數值模擬。為了比較，式（1）和式（9）中系統參數和狀態轉換參數的取值對應相同。考慮只有一個社交網絡內部的成員相互感染的情況，即取n= 1。根據實際物理意義，參數的取值以“小時”為單位，假設社交網絡中每小時新加入的成員平均為1，所以取B= 1，社交網絡用戶退群的用戶比率比較小，假設為10-3數量級，取μS=μI=μR= 0.008，已感染節點的免疫率取α= 0.003，感染率取β= 1×10-6，另外，假設社交網絡中活躍用戶數為m= 50。當不引入預先控制措施時，式（1）中取φ的值為0。式（9）中φ的值是隨時空變化的，其值通過迭代計算求得，其中，取κ= 10。S，I，R和λ的取值分別為:S(0)= 990，I(0)= 1，R(0)= 1，λ1=λ2=λ3= 0。仿真結果如圖2所示。

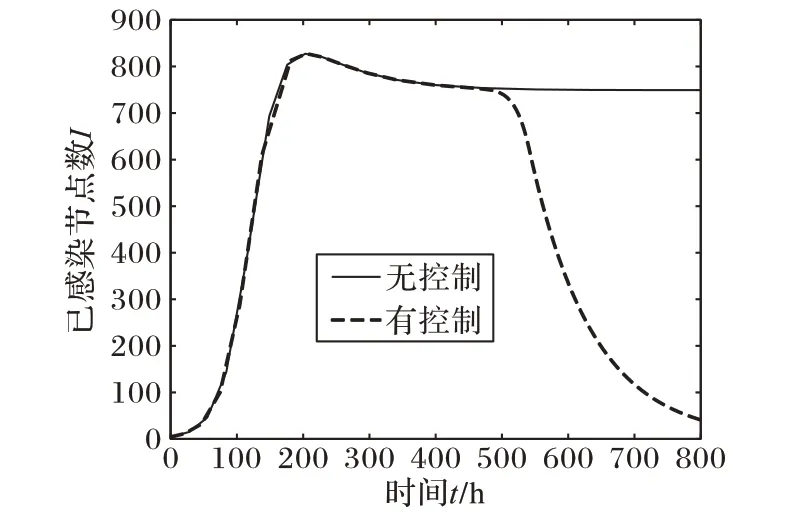
圖2 系統（1）和（9）的比較Fig.2 Comparison of system（1）and（9）

觀察圖2發現，在不良信息擴散的前期（t＜500），有控制策略和無控制策略的傳播速度和規模沒什么區別，當t＞500時，采取控制措施明顯抑制了不良信息的擴散。出現這種現象的原因是，在不良信息擴散的前期，控制函數的φ的值一直持續為0，隨著時間的推移，控制函數的取值不斷增大，從而控制策略發揮作用。圖2對應的控制函數φ的變化曲線如圖3所示。

圖2和圖3表明，控制函數取值的變化對不良信息擴散的控制有顯著效果，說明建立帶有優化控制函數的信息擴散模型，可以有效刻畫信息擴散過程，而且可以通過調節控制函數的取值隨機控制信息擴散過程。這一結論揭示了，從理論上可以將自動控制理論和網絡信息擴散模型融合起來，實現不良信息擴散以及控制規律的建模，從而為不良網絡信息傳播控制提供理論指導。另一方面，依據模擬結果，從現實管理角度來看，可以根據實際網絡運行狀態采取不同等級的時空控制策略。

2）當式（1）中控制策略φ的值固定，且社交網絡個數n=1時，本文式（1）就是傳統的SIR模型。將本文引入優化控制策略后和傳統模型進行比較，取式（1）中φ=0.003，其余參數取值同圖2，數值模擬式（1）和式（9），仿真結果如圖4所示。

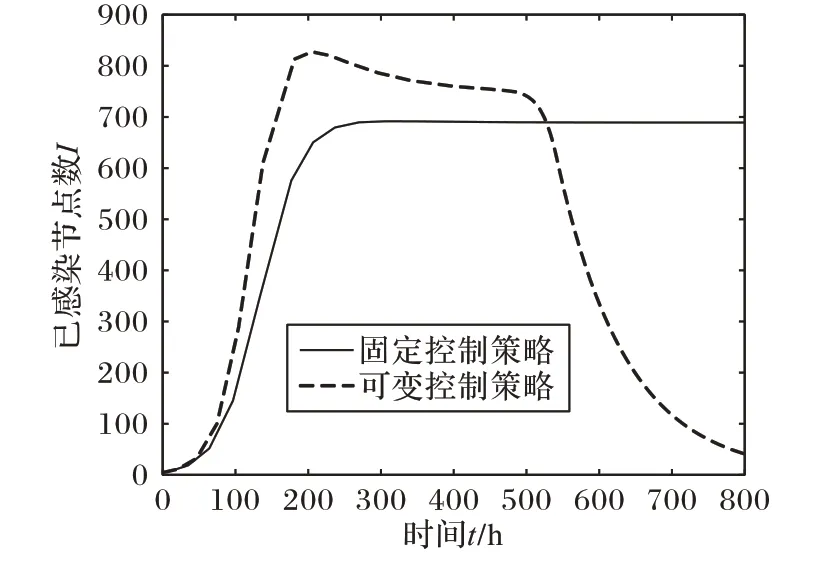
圖4 固定控制策略和可變控制策略比較Fig.4 Comparison of fixed control strategy and variable control strategy

從圖4 可以看出，在感染的初始階段（大約t＜250），不管是采用固定控制策略還是可變控制策略，已感染節點數都是呈快速上升趨勢，這是因為，初始階段社交網絡中大多數都是易感染節點，單位時間內轉化為已感染節點的數目也多。另外，在感染期t＜500時段，采用可變的控制策略反而會導致已感染節點增長速率和規模更大，這是因為控制措施在起初比較弱的原因（見圖3），隨著時間的推移，控制策略逐漸增強，已感染節點數呈明顯下降趨勢。這表明，在實際網絡安全管理中，應該結合安全態勢感知系統，靈活調節控制策略，以達到安全投入最佳性能。

3）為了比較本文模型和傳統模型的不同（即，考慮交叉感染和不考慮交叉感染），觀察不同社交網絡間交叉感染對不良信息擴散的影響程度，取系統（1）中社交網絡個數為1 和2兩種情況進行比較，即取n= 1 和n= 2，其余參數的取值和圖2相同。比較結果如圖5所示。

圖5 有交叉感染和沒有交叉感染的比較Fig.5 Comparison of condition with cross infection and condition without cross infection

圖5 表明當出現交叉感染時，明顯不良信息的擴散從速度和規模上都遠遠大于沒有交叉感染的情況，出現這種現象的原因主要是當一個感染源可以感染多個社交網絡的節點時，易感染節點數會增多，這種現象與現實中的認識是一致的。而事實上，在線社交網絡是現實社交群體的映射，存在交叉感染是一定的，所以從圖5 的曲線可以看出，傳統不考慮交叉感染的模型（即n=1）存在對不良信息擴散規模與速度偏低估計的情形。

4 結語

考慮到在線社交網絡的形成是現實社會中人們社交關系的體現，本文將社交關系網看作無向連通圖，根據圖論中節點間的連通性構建了社交網絡中不良信息擴散模型，與已有模型的不同之處是，本文將最優控制理論引入模型中，將不良信息擴散的控制策略設置為一個變量，管理員可以根據當前網絡運行狀態采取不同程度的控制措施。根據最優理論證明了最優控制策略的存在性，并且求出最優控制策略的數學表達式，得到了具有最優控制策略的不良信息擴散控制模型。最后，數值仿真實驗結果表明，采取優化控制策略可以有效抑制不良信息的擴散，并且在給定相應參數的情況下，得到了優化控制函數的變化曲線。實驗結果表明，可以通過調整相關參數改變不同時段控制策略的強度。另外，實驗模擬了社交網絡間相互有信息傳遞和無信息傳遞時，信息擴散的快慢和規模。結果表明，社交網絡間如果是相互連通的，也就是說信息可以互相傳遞，那么不良信息擴散的規模和速度都會增大。這一現象與現實反映的情況是一致的。今后將收集實際數據驗證模型的效果。