基于SEM 圖像的煤層氣滲流裂隙開度影響的模擬研究

曹栩樓，劉江峰，倪宏陽，楊典森，孟慶彬

（1.中國礦業大學 深部巖土力學與地下工程國家重點實驗室，江蘇 徐州221116；2.中國礦業大學 力學與土木工程學院，江蘇 徐州221116；3.中國科學院武漢巖土力學研究所，湖北 武漢430071）

煤作為一種復雜的多孔介質材料，其表面和內部遍布了各種孔隙和裂隙結構。在這些孔裂隙結構中蘊藏著大量的煤層氣，是氣體吸附存儲和游離擴散的主要場所，因此煤的孔裂隙結構特征是決定煤層氣儲存和運移的主要因素。由于煤的非均勻性和各向異性，對其進行有效的表征并在煤層氣滲流運移規律的研究中考慮其影響變得十分重要。對于掃描電鏡技術（SEM），由于其較低的測試成本和良好的成像效果，被廣泛應用于各個領域[1-6]。常規的煤滲透率是通過宏觀氣體滲透實驗獲得的，但該方法無法了解氣體的滲流運移過程，無法對其細觀機理進行有效的研究。使用數字圖像技術提取出煤體裂隙結構，通過求解Stokes 方程來計算氣體的動力特性，同時建立了對應的滲透率計算模型，為探究氣體滲流運移機理提供了一種重要的方法。另外通過定量化的建模，模擬了煤層氣在不同開度的裂隙中運移過程，研究了滲透率與裂隙開度之間的關系。

1 電鏡掃描和圖像處理

采用中國礦業大學現代分析與計算中心的Quanta250 型掃描電子顯微鏡對來自陜西榆林的煤樣進行SEM 成像。SEM 掃描得到煤樣微觀結構數字圖像一般不能直接用于定量研究，需要對圖像進行一系列的后處理，其中最重要是對圖像進行準確的分割、二值化，來提取出其中的孔裂隙結構[7-8]。

從原始的SEM 圖像中可以看到明顯的煤裂隙結構，其為氣體運移的主要通道。使用MATLAB 開發相應程序，設定合理的分割閾值對數字圖像進行二值化，提取出其中的裂隙結構，煤SEM 圖像及對應二值圖如圖1。

圖1 煤SEM 圖像及對應二值圖Fig.1 SEM image of coal and corresponding binary diagram

2 氣體運移及滲透率計算模型

在COMSOL Multiphysics 中，對于氣相流體，通過求解Stokes 方程可以模擬裂隙中氣體運移的過程，其表達式為：

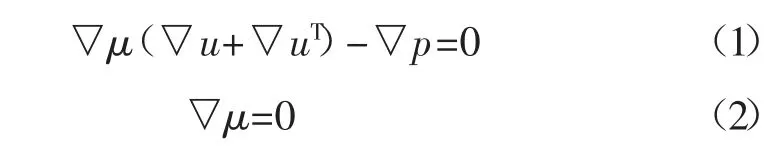
式中：p 為氣體壓力，Pa；u 為流體速度場；μ 為流體的動力黏度，Pa·s。

根據SEM 數字圖像二值化后的裂隙形態進行建模，煤樣的尺寸為510 μm×595 μm，由于裂隙尺度遠大于孔隙，流體主要通過裂隙管道進行運移，因此只考慮氣體在裂隙中流動，對裂隙進行網格化，氣體運移數值模型如圖2。模型參數取值：流體密度ρ 為0.716 kg/m3，流體動力黏度μ 為11.067 Pa·s，入口端氣體壓力p0為1 MPa。

通過求解Stokes 方程可以得到流體穩態后在裂隙中的速度分布，對裂隙出口端的流體速度進行積分，可以求得出口端的流量，其表達式為：

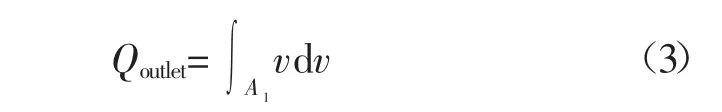
式中：Qoutlet為裂隙出口端流量，m3/s；A1為裂隙出口端面積，m2；v 為裂隙出口端速度m/s。

煤樣的滲流可以用Darcy 定律來描述：

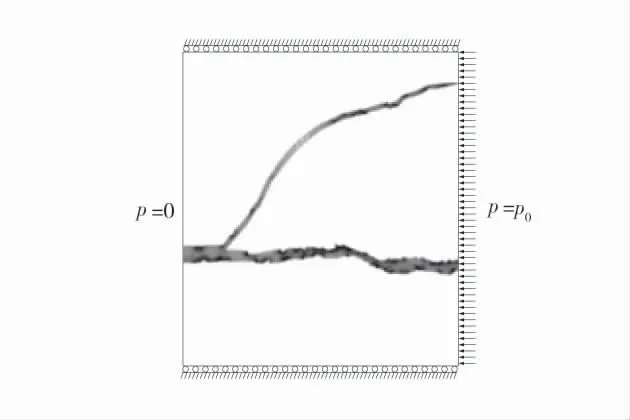
圖2 氣體運移數值模型Fig.2 Numerical model of gas migration

式中：Q 為通過煤樣的氣體流量，m3/s；k 為滲透率，m2；A2為煤樣的橫截面積，m2；l 為煤樣長度，m；△p 為裂隙入口端與出口端的壓力差。

氣體主要是在裂隙結構中運移，因此裂隙出口端流量近似等于通過煤樣的總流量，所以推導出基于圖像裂隙結構模型的滲透率計算模型，表達式為：

3 模擬結果

3.1 原圖中煤層氣運移結果

通過模擬得到了煤層氣在圖1 裂隙結構中運移的動力特性，煤層氣在裂隙中的滲流速度分布如圖3。

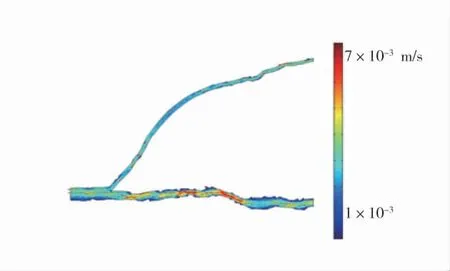
圖3 煤層氣在裂隙中的滲流速度分布Fig.3 Seepage velocity distribution of coalbed methane in fractures

從圖3 可以看出，當煤層氣從裂縫開度較大處運移到裂縫開度小的地方，流體速度會明顯增加。根據設置在裂縫中的監測點，計算得到裂縫開度較大的通道，其平均流動速度較大。而流體速度會影響試樣的滲透率，因此裂隙開度與滲透率之間存在一定的相關性。

根據式（6）計算出煤樣圖像對應的滲透率，并將結果與實驗室使用穩態法測試得到的滲透率結果進行對比，滲透率數值模擬結果與實驗結果對比如圖4。

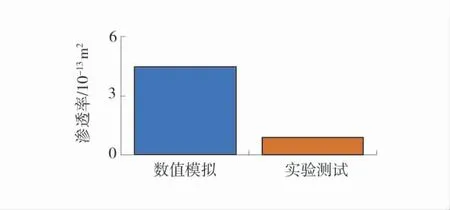
圖4 滲透率數值模擬結果與實驗結果對比Fig.4 Comparison of permeability results between numerical simulation and experiment

由于在實驗室測試中，不可避免的需要施加圍壓，因此會導致煤樣的孔隙率下降，進而使煤樣的滲透率與拍攝SEM 圖像時煤樣的滲透率相比，結果偏小，存在一定的誤差。基于數字圖像建立的滲透率模型預測結果與實驗相比，該誤差在合理范圍。因此本文的滲透率計算模型是有效、合理的，為滲透率的預測提供了一種新的有效方法。

3.2 煤層裂縫開度的定量研究

為了定量化研究裂縫開度對氣體運移的影響，通過建立不同裂縫開度的模型，并通過式（6）計算其滲透率，來探究裂縫開度對滲透率的影響。在保持裂隙結構其他變量不變的前提下，分別建立了裂隙開度b 為5.5、11、22、44 μm 的數值模型，同時在裂隙中設置6 個監測點，用以觀察不同開度的裂隙中速度變化，不同裂縫開度模型的氣體速度場分布及監測點位置示意圖如圖5，不同裂隙開度監測點氣體流速如圖6。從圖中可知，改變裂隙開度對流體運移的速度分布密度沒有影響。通過計算監測點的速度，發現裂隙的開度越大，流體的速度也越大。

通過式（6）計算出圖5 中不同開度模型的滲透率，不同裂隙開度下煤層氣滲透率見表1。

可以發現，隨著裂隙開度的增大，滲透率變化明顯，最大相差2 個數量級。為了定量分析裂隙開度與滲透率之間的關系，將裂隙開度與滲透率之前進行擬合，不同裂隙開度滲透率及基本流動模型曲線圖如圖7。

根據裂隙流動基本模型[9]，滲透率kf與裂隙開度b 之間滿足如下關系：

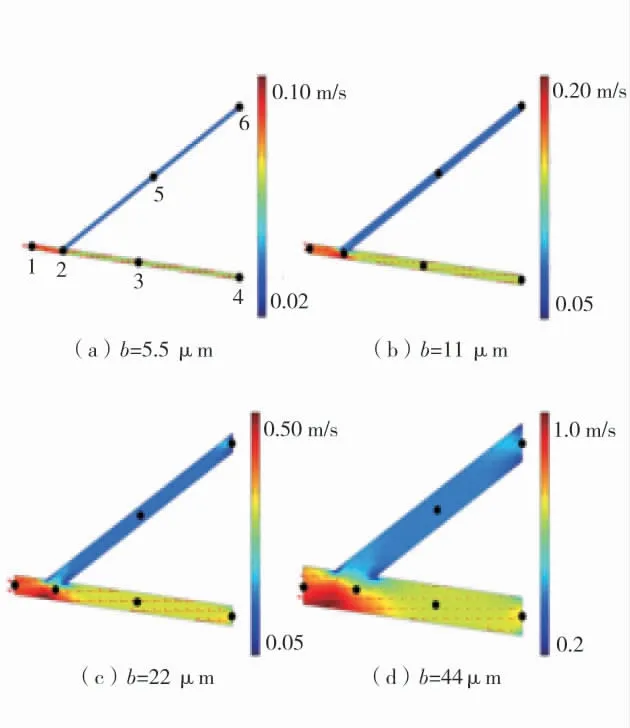
圖5 不同裂縫開度模型的氣體速度場分布及監測點位置示意圖Fig.5 Distribution of gas velocity field and location of monitoring points for fracture models with different opening degrees

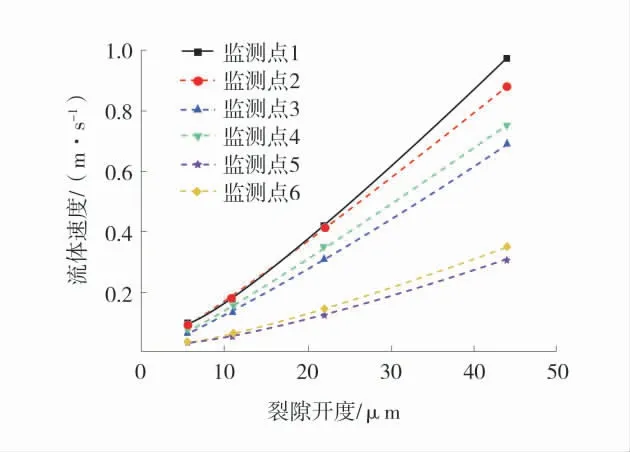
圖6 不同裂隙開度監測點氣體流速圖Fig.6 Gas velocity diagram of monitoring points with different opening degrees

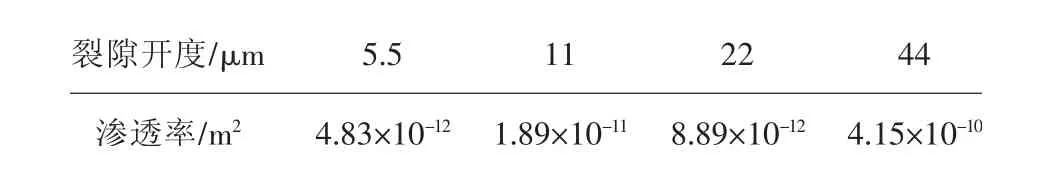
表1 不同裂隙開度下煤層氣滲透率Table 1 Coalbed methane permeability of fracture models with different opening degrees

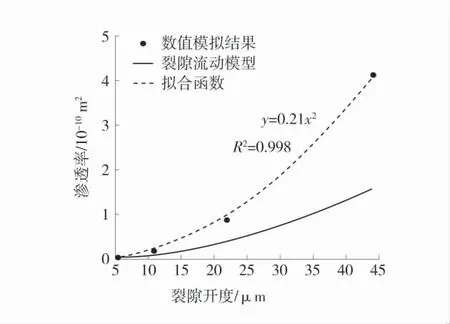
圖7 不同裂隙開度滲透率及基本流動模型曲線圖Fig.7 Curves of permeability and basic flow models with different fracture opening degrees

從圖7 可以發現，裂隙流動基本模型與擬合的模型之間存在一定的誤差，數值模擬的滲透率結果要大于絕對滲透率。這是由于煤層氣滲流運移過程中存在克林肯伯格（Klinkenberg）效應，氣體分子在裂隙中運移時，并不會完全附著在管道上，而會沿著管壁滑動。根據Klinkenberg 的研究，有效滲透率與氣體壓力之間的關系為[10]：

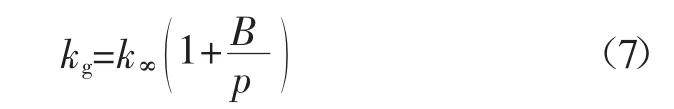
式中：kg為考慮Klinkenberg 效應的氣體滲透率，m2；k∞為流體壓力很大以至于Klinkenberg 效應不再起作用時的絕對滲透率，m2；B 為Klinkenberg因子，Pa。

k∞和B 取決于試樣本身的性質。考慮Klinkenberg 效應時，通過規劃求解求出煤樣的Klinkenberg因子B＝1.5 MPa。修正后裂隙流動模型為：

4 結 論

1）SEM 數字圖像能夠直接觀察到煤樣裂隙形態特征，通過實際裂隙結構來建立數值模型，是一種對煤樣非均勻性表征的有效方法。

2）基于數字圖像中煤裂隙結構建立的氣體滲透率預測模型，通過與實驗室測試結果比較，具有良好的準確性，是一種有效的滲透率計算方法。

3）定量化分析裂縫開度對氣體滲透率的影響，發現裂隙開度越大，氣體流速增加，滲透率變大。

4）氣體在裂隙運移過程中存在Klinkenberg 效應，通過擬合求出煤樣的滑脫因子，并修正了氣體裂隙流動模型。