鋼絲繩股內鋼絲張力分布及鋼絲間摩擦力研究

陳 穩，李 倫，李濟順，鄭培培，許世鈺

1河南科技大學河南省機械設計及傳動系統重點實驗室 河南洛陽 471003

2河南科技大學機電工程學院 河南洛陽 471003

鋼 絲繩作為一種高強度柔性構件，具有良好的拉伸性能，因而廣泛應用于工業、礦山、交通和旅游等領域。在長期的軸向拉力作用下，鋼絲繩在軸向方向會產生較大的變形。同時，側絲與中心絲間會因拉伸變形而產生相對滑動，在摩擦力作用下側絲與中心絲間產生磨損[1]，在磨損處產生應力集中及疲勞微裂紋，降低鋼絲的疲勞壽命和抗拉強度[2]。因此，有必要對鋼絲繩股內鋼絲的張力分布、側絲與中心絲間的摩擦力進行研究。

諸多學者已對鋼絲繩內鋼絲的張力分布和繩絲間的摩擦力做了大量的理論和仿真研究，但由于鋼絲繩具有復雜的空間螺旋纏繞結構，使得理論分析、有限元仿真和試驗研究等單一的方法難以對繩絲的張力分布和繩絲間的摩擦力進行準確分析。文獻 [3]基于細桿理論對鋼絲的受力進行了數值分析，但其忽略了鋼絲間的摩擦力。文獻 [4]在文獻 [3]的基礎上在接觸點處加入界面力，建立了具有徑向接觸的力學模型，分析了側絲的軸向滑移對中心絲的影響，但模型較為復雜，同時結論表明隨著軸向拉伸載荷的增加，鋼絲繩股內鋼絲間接觸狀態由側絲-芯絲-側絲接觸轉變為芯絲-側絲接觸。文獻 [5]利用微單元法，根據微弧兩端的力與微弧纏繞角的關系建立了平衡方程，推導出鋼絲間接觸力的公式。文獻 [6]推導出一個細絲纏繞在一個圓柱上時所承受的徑向壓力公式，但其忽略了側絲的半徑。文獻 [7]采用解析方法，研究了鋼絲之間的接觸對鋼絲繩力學性能的影響，并利用共軛梯度法和快速傅里葉變換計算出鋼絲間的接觸變形。文獻[8]通過有限元軟件分析了繩絲間接觸摩擦力對有限元結果的影響，結果表明摩擦力對于鋼絲應力分布、軸向位移的影響很重要。文獻 [9]等利用有限元軟件對直線拉伸狀態下 1+6 型鋼絲繩進行了受力分析，結果表明芯絲比側絲承受的拉伸載荷大。文獻 [10]對彎曲狀態下鋼絲繩進行了有限元仿真，得到了鋼絲繩股內鋼絲張力分布規律。

上述文獻大多通過單一的理論分析或有限元方法對鋼絲繩股內繩絲的力學性能進行了研究，但并未涉及繩絲張力與繩絲間摩擦力的關系。筆者以直線拉伸狀態下的 1+6 型鋼絲繩作為研究對象，基于圓柱螺旋彈簧理論建立鋼絲繩股內側絲的受力模型，依據側絲與中心絲在鋼絲繩軸向承載方向變形量相等建立其側絲-中心絲的力-位移平衡方程，推導出側絲與中心絲間的摩擦力關系式；同時結合試驗測試和有限元分析等方法對鋼絲繩繩絲的張力分布及側絲與中心絲間的摩擦力進行分析研究，為鋼絲繩繩絲張力的測試和繩絲間的摩擦力計算分析提供理論和試驗依據。

1 側絲-中心絲摩擦力分析

1.1 建立力學模型

鋼絲繩是由鋼絲按照一定的規則捻制而成的且具有復雜空間螺旋結構的柔性構件。圖 1 所示為 1+6 型鋼絲繩結構示意，該鋼絲繩是由 1 根中心絲和 6 根繞中心絲螺旋纏繞的側絲組成，7 根鋼絲直徑均等。

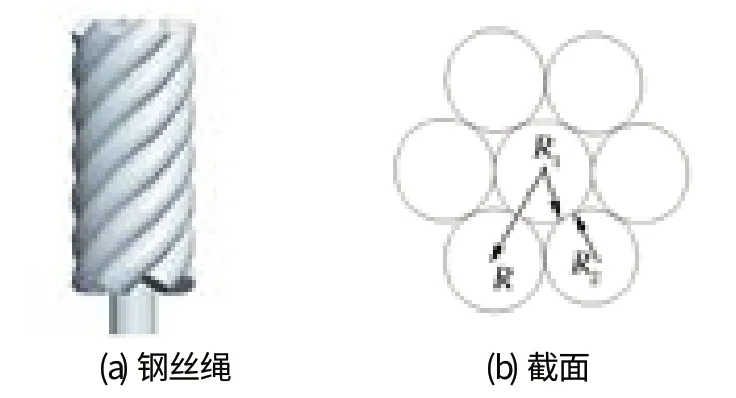
圖1 1+6 型鋼絲繩結構示意Fig.1 Structural sketch of 1+6 type wire rope

繞中心絲螺旋纏繞的側絲與圓柱螺旋彈簧具有類似的螺旋結構，且兩者在軸向載荷作用下產生的徑向變形均遠小于軸向變形，因此可把鋼絲繩股中的每根側絲視為一個圓柱螺旋彈簧模型。在建立側絲圓柱彈簧模型時需做以下假設：

(1) 僅考慮側絲與中心絲間的相互作用；

(2) 忽略側絲間的相互作用，即 6 根側絲可視為 6個獨立的并聯彈簧；

(3) 側絲與中心絲間的摩擦力方向與鋼絲繩所受拉力的方向一致；

(4) 側絲與中心絲間的摩擦力與測試鋼絲繩長度呈線性關系。

1.2 鋼絲受力分析

截取一微段 1+6 型鋼絲繩，結合文獻 [11]中側絲受力分析圖，對側絲和中心絲進行受力分析，如圖2 所示。鋼絲繩在拉力F作用下，當側絲與中心絲間不存在摩擦力時，中心絲在拉力方向上僅存在軸向力FH，側絲在拉力方向上僅存在軸向力FT；當側絲與中心絲間存在摩擦力時，中心絲在拉力方向存在軸向力FH和摩擦力 6f，二者的合力為軸向張力Fh，側絲在拉力方向存在軸向力FT和摩擦力f，二者的合力為軸向張力Ft。

圖2 側絲與中心絲的受力分析Fig.2 Force analysis of outer wire and central wire

側絲在中心線切線方向的張力

式中：E為鋼絲的彈性模量，MPa；A為側絲的橫截面面積，mm2；ε為側絲應變。

側絲在鋼絲繩拉力方向的軸向張力

式中：α為側絲的螺旋角，(°)。

在實際使用過程中，鋼絲繩的中心絲與側絲在拉力方向均產生相等的變形。根據文獻 [12]和文獻 [13]關于拉伸桿件剛度和彈簧剛度的相關理論，可以求得中心絲剛度KH和側絲剛度KT。若忽略鋼絲繩內摩擦，即中心絲和側絲僅受軸向力FH和FT作用時，由力、剛度和變形之間的關系可得

式中：KH為中心絲的剛度，N/mm；KT為螺旋側絲的剛度，N/mm。

當中心絲和側絲間存在摩擦時，摩擦力為鋼絲繩的內力，則有

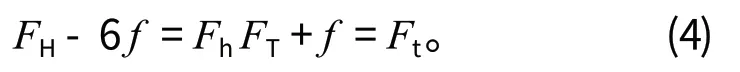
由式 (3)、(4) 可得

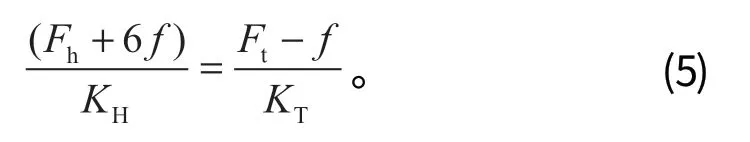
根據中心絲的軸向張力Fh和側絲的張力Fc之間的關系可得

令KH/KT=λ，由式 (2)、(5)、(6) 可得

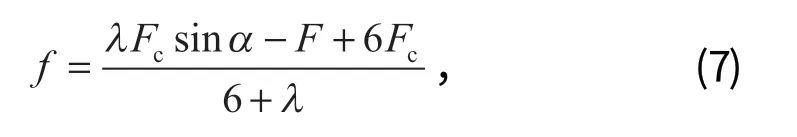
式中：f為單根側絲與中心絲間在拉力方向的摩擦力。

則一個捻距內鋼絲繩股內側絲與中心絲間在拉力方向上摩擦力

式中：n為鋼絲繩在測定長度為L時的捻距數量，個。

由式 (8) 可知，只要測量出鋼絲繩在直線拉伸狀態下其側絲在中心線切線方向的張力Fc，依據鋼絲繩所施加的軸向拉力載荷F和鋼絲繩的長度L，即可定量計算出鋼絲繩側絲與中心絲間的摩擦力。

2 直線拉伸鋼絲繩張力試驗

2.1 試驗設計

搭建鋼絲繩直線拉伸狀態張力測試實驗臺，如圖 3 所示。實驗臺由機架、立柱、天輪和加載裝置等部分組成。試驗鋼絲繩由兩部分組成：試驗鋼絲繩段6 以及牽引鋼絲繩段 4 和 9。試驗鋼絲繩作為被測對象，其主要技術參數[14]如表 1 所列。牽引鋼絲繩段 4一端通過拉力傳感器與試驗鋼絲繩段連接，另一端經過左滑輪纏繞并固定在加載裝置的卷筒上；牽引鋼絲繩段 9 一端通過與拉力傳感器與試驗鋼絲繩段連接，另一端經右滑輪固定在機架底座上，通過加載裝置手輪以手動方式對鋼絲繩施加拉力載荷。

圖3 實驗臺模型Fig.3 Model of test bench

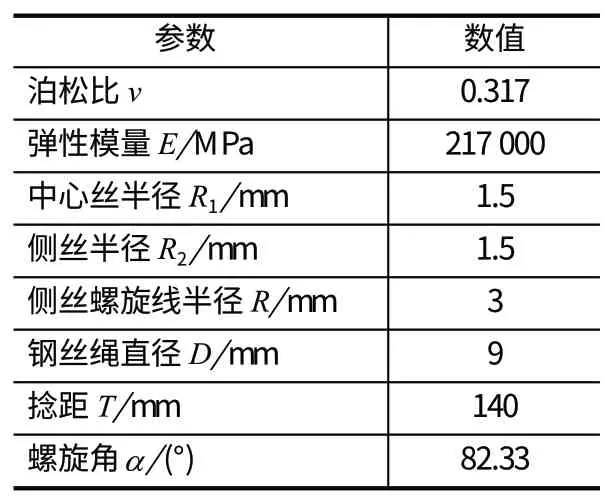
表1 試驗用鋼絲繩的主要技術參數Tab.1 Main technical parameters of testing wire rope

在試驗鋼絲繩段上粘貼光纖布拉格光柵傳感器(Fiber Bragg Grating，FBG)，如圖 4 所示，共a、b、c3 組傳感器、21 根傳感器，其中 18 根光纖傳感器粘貼在側絲上，每個通道的最后一根光纖傳感器懸空放置作為溫度補償。試驗測定沿側絲中心線切線方向的張力值，通過加載裝置手輪施加拉力至指定的數值，由拉力傳感器確定鋼絲繩拉力值，待光纖傳感器的測試值穩定后，記錄數值并根據文獻 [15]計算側絲的張力值。

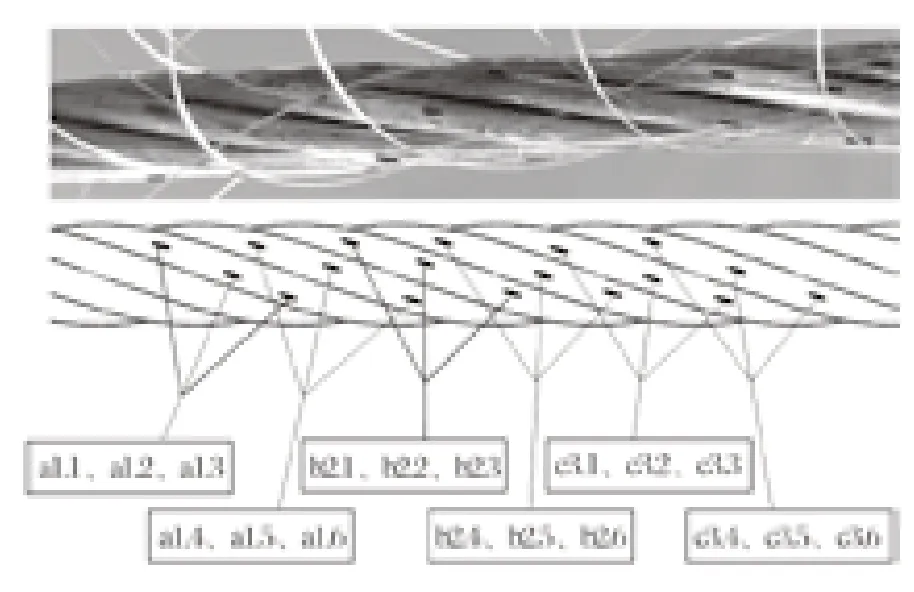
圖4 FBG 傳感器的粘貼方式Fig.4 Sticking mode of FBG sensor

2.2 試驗結果

試驗選取的拉力值為 6 000、7 000、8 000、9 000和 10 000 N，取各拉力下側絲張力的平均值作為沿側絲中心線切線方向的張力值，依據試驗張力值并根據式 (2) 和式 (8) 計算得到側絲沿拉力方向的軸向張力和側絲與中心絲間的摩擦力，如表 2 所列。

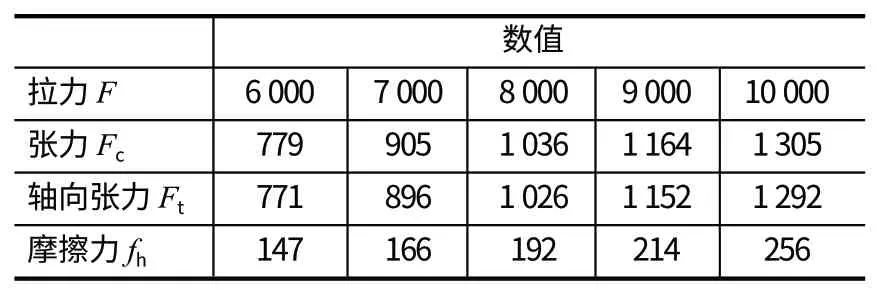
表2 不同拉力下的試驗結果Tab.2 Test results at various tension N

3 鋼絲繩有限元仿真

3.1 鋼絲繩三維模型與有限元模型

在直線拉伸狀態下，1+6 型鋼絲繩股內側絲中心線是一次空間螺旋線，螺旋線的參數方程[16]為

式中：t為螺旋線轉角，(°)。

利用 Pro/E 軟件建立鋼絲繩的三維實體模型，所需技術參數如表 1 所列。Pro/E 軟件具備插入曲線的功能，在 Pro/E 軟件中插入側絲中心線的參數方程，繪制側絲中心線，分別通過可變截面掃掠命令和拉伸命令生成各側絲的實體[17]，三維實體模型如圖 1(a) 所示。

將三維實體模型導入 ABAQUS 軟件中，建立有限元模型。根據表 1 中的主要技術參數賦予實體模型材料屬性。設置網格單元類型為八節點線性六面體單元，使用掃掠劃分技術對鋼絲進行網格劃分[18]。設置側絲與中心絲間的接觸類型為通用摩擦接觸，在鋼絲繩使用初期，鋼絲間的潤滑性良好，鋼絲間的摩擦力較小，設定摩擦系數為 0.05[19]。在鋼絲繩兩端面中心處各建立一個參考點，利用 coupling 命令將參考點與端面耦合，沿鋼絲繩的軸線方向對參考點施加拉力，分析步時間為 0.01 s，選取拉力為 6 000、7 000、8 000、9 000 和 10 000 N，有限元模型如圖 5 所示。

3.2 有限元仿真結果

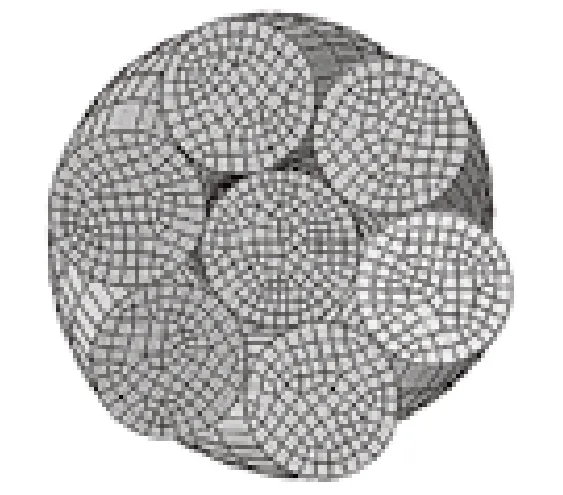
圖5 鋼絲繩有限元模型Fig.5 Finite element model of wire rope

在 ABAQUS 軟件后處理模塊中，通過 Report 工具中 Free Body Cut 指令可以得到沿鋼絲繩中心線方向側絲截面的軸向張力。

以鋼絲繩中心線方向作為橫坐標，側絲截面的軸向張力為縱坐標，繪制在拉伸時側絲軸向張力分布如圖 6 所示，圖中 B、C、D、E、F 和 G 為各側絲軸向張力曲線編號。由圖 6 可知，各側絲軸向張力具有相同的分布趨勢，側絲張力隨著鋼絲繩拉力的增強而呈現增大趨勢；不同拉力下同一根側絲各截面最大差值為 7 N，同一根側絲各截面上軸向張力基本相等。因此，可以認為同一拉力下各側絲的軸向張力基本相等，取各側絲軸向張力的平均值作為側絲的軸向張力。

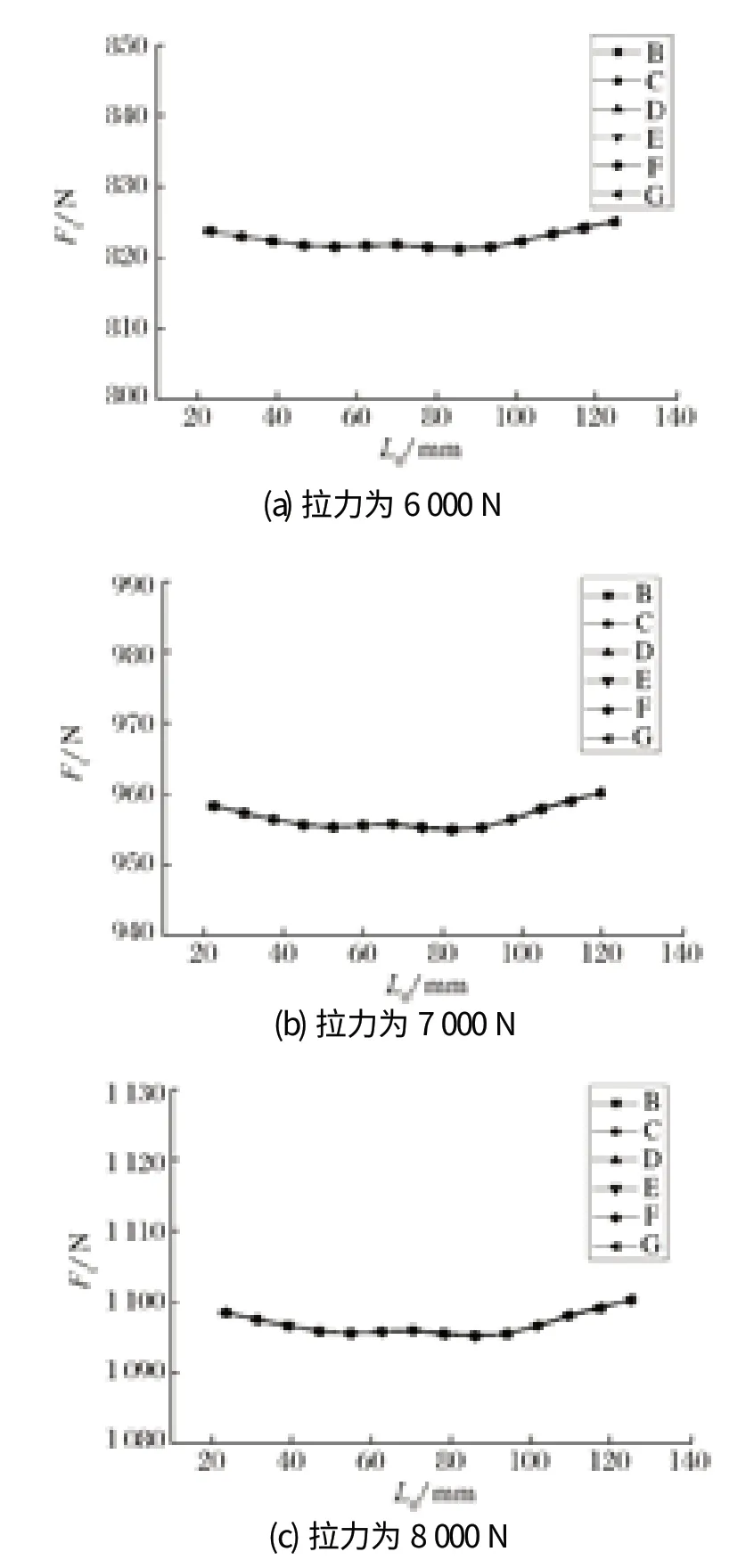
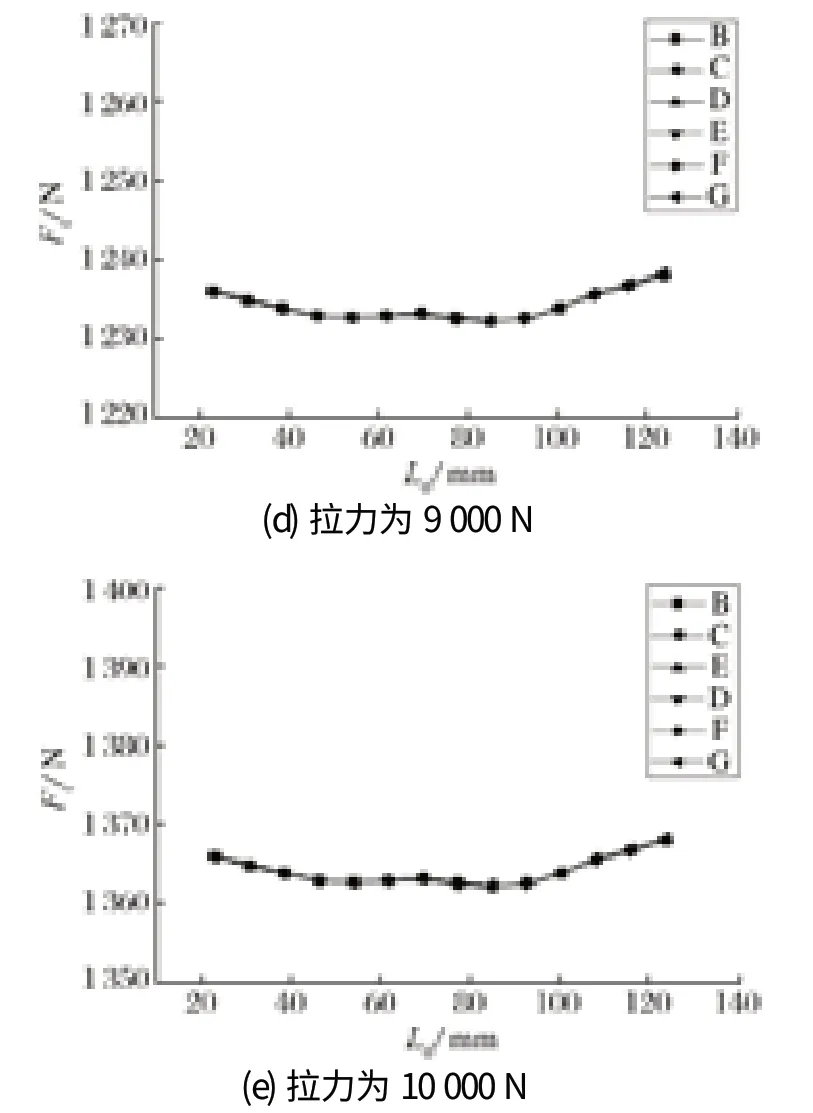
圖6 拉伸時側絲的軸向張力分布Fig.6 Distribution of axial tension of outer wire in stretching mode

側絲與中心絲外表面均為曲面，無法通過ABAQUS 軟件直接計算兩者之間的摩擦力，可以通過庫倫模型計算[20]，即

式中：P為側絲與中心絲間的法向接觸力，N；Q為側絲與中心絲接觸區域上所有節點的接觸壓強之和，MPa；S為側絲與中心絲接觸面積，mm2；N為側絲與中心絲接觸區域上節點數量，個；μ為摩擦因數。

不同拉力下側絲與中心絲間接觸面上的節點數和接觸面積基本相同，只是接觸面上的接觸壓強大小不同。現僅給出拉力為 10 000 N 時，一個捻距內側絲與中心絲間的接觸壓強和接觸面積，如圖 7、8 所示。

根據提取的仿真數據和式 (10)、(11)，計算不同拉力下側絲的軸向張力和一個捻距內側絲與中心絲間的摩擦力，結果如表 3 所列。

4 驗證及分析

4.1 側絲軸向張力試驗與仿真對比分析

以鋼絲繩拉力值作為橫坐標，以側絲軸向張力的試驗值和仿真值作為縱坐標繪制對比結果，如圖 9 所示。由圖 9 可知，試驗值與仿真值基本吻合，說明本文使用粘貼光纖的方法測定側絲的張力具有一定的可行性。

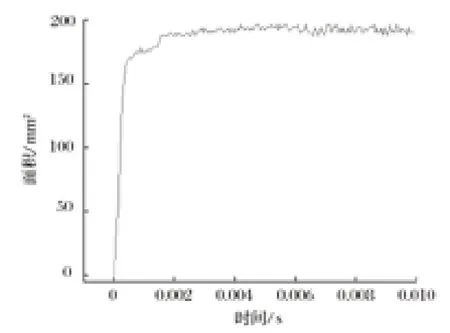
圖7 側絲與中心絲間的接觸面積Fig.7 Contact area between outer wire and central wire

圖8 側絲與中心絲間的接觸壓強Fig.8 Contact pressure between outer wire and central wire

表3 不同拉力下的仿真結果Tab.3 Simulation results at various tension N

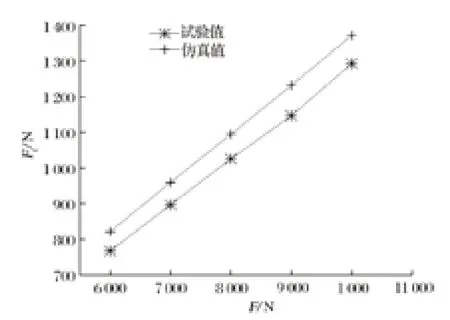
圖9 側絲軸向張力的試驗值與仿真值Fig.9 Tested values and simulated ones of axial tension of outer wire

同時試驗值與仿真值也存在誤差，主要原因有以下兩方面。

(1) 模型誤差 在分析鋼絲繩受力模型時，忽略了側絲與側絲之間的作用力，而實際上鋼絲繩側絲與側絲之間不但存在擠壓力，同時還存在著摩擦力。因此，建立理想化鋼絲繩受力模型時忽略側絲之間的作用力是本研究結果產生誤差較大的原因之一。在本研究中，該誤差無法消除和減小。

(2) 測試誤差 筆者采用光纖傳感器測量鋼絲的張力，使用粘接劑將光纖傳感器與鋼絲粘貼在一起，由鋼絲的變形引起粘接劑的變形，進而引起光纖的透射譜和反射譜發生變化。根據光纖的透射譜和反射譜發生變化，可以計算得到鋼絲的應變和張力，這是利用光纖傳感器測量張力的基本原理。膠貼式的方法雖具有線性好、操作簡單的優點，但由于鋼絲與光纖傳感器的直徑尺寸比較小，光纖粘貼的方位、粘接劑層的厚度難以精確控制，致使試驗產生誤差。

上述造成試驗存在誤差的因素暫時沒有更好的辦法克服。目前雖然有新型的光纖金屬化焊接方法，但同樣由于鋼絲與光纖傳感器的直徑尺寸比較小，難以保證焊接精度，所以未采用該方法。為減小試驗誤差，可以增加試驗次數，對數值接近的張力求平均值。

4.2 側絲-中心絲摩擦力計算與仿真對比析

以鋼絲繩拉力值作為橫坐標，以一個捻距內摩擦力的仿真值和計算值作為縱坐標繪制對比結果，如圖10 所示。由圖 10 可知，計算值與仿真值基本一致，說明本文所建側絲模型和推導的摩擦力關系式具有一定的合理性。

圖 10 側絲與中心絲間摩擦力的試驗值與仿真值Fig.10 Tested values and simulated ones of friction between outer wire and central wire

同時計算值與仿真值也存在誤差，主要原因有以下兩方面。

(1) 模型誤差 本研究把側絲簡化為彈簧模型，而該彈簧模型的直徑與側絲的直徑相差不大，其受力情況與真實的彈簧存在一定誤差，這是產生計算值與仿真值誤差的主要原因。

(2) 假設誤差 忽略了側絲與側絲的相互作用。實際上側絲間是有相互作用的，這種作用對側絲-中心絲的摩擦力也有一定的影響。此外，筆者研究摩擦力與張力之間的關系，張力測定試驗中存在的誤差也直接導致計算值與仿真值出現誤差。

5 結論

推導了側絲與中心絲間的摩擦力關系式，通過鋼絲繩側絲的張力測定試驗，得到了側絲的張力分布，并以此計算得到側絲與中心絲間的摩擦力。通過有限元分析軟件分別仿真計算出側絲的張力分布和側絲與中心絲間的摩擦力。

(1) 側絲與中心絲間的摩擦力隨著鋼絲繩拉力的增加而呈現增大的趨勢，一個捻距內摩擦力約占軸向載荷的 2.7%。

(2) 鋼絲繩股內各側絲張力均隨著鋼絲繩拉力的增加而增大。同一拉力下鋼絲繩股內各側絲張力相等，中心絲比側絲承受的載荷大，中心絲和側絲分別承擔約 18.4% 和 81.6% 的軸向載荷。