基于HNC-21T數控系統非圓曲線輪廓宏指令編程的應用研究

楊光龍 王華麗 劉芳

摘?要：非圓曲線輪廓即公式曲線輪廓，宏程序在解決非圓曲線輪廓和復雜工件輪廓加工中得到了廣泛的應用，但對于很多計算機高級語言編程基礎較差或者是數學計算能力較差的數控車削加工編程人員來說常常難以掌握。通過對華中數控車削HNC-21T系統公式曲線輪廓宏指令編程的分析、計算研究，形成了數控車削系統公式曲線輪廓宏指令編程的模板，使數控編程人員在生產實踐中，只要能看懂生產零件圖，根據編程模板，就可以快速、準確地編寫出復雜工件輪廓的數控加工程序。

關鍵詞：數控車;非圓曲線;宏指令;編程

中圖分類號：TG527文獻標識碼：A開放科學（資源服務）標識碼

doi：10.14031/j.cnki.njwx.2020.06.006Open Science Identity（OSID）

Application Research on Macro Command Programming of Non-circular

Curve Profile Based on HNC-21T CNC System

Yang Guanglong，Wang Huali，Liu Fang

（Guizhou Agricultural Vocational College，Guiyang 551400，China）

Abstract： Non-circular curve contour is the formula curve contour.?Macro program has been widely used in solving non-circular curve contour and complex workpiece contour machining， but it is often difficult for many CNC turning programmers who have poor basic programming language or poor mathematical calculation ability.By analyzing and calculating the macro command programming of formula curve contour of HNC-21T system in Huazhong CNC turning， the macro command programming template of formula curve contour of CNC turning system is formed， which enables CNC programmers to quickly and accurately write the CNC machining program of complex workpiece contour as long as they can understand the production part drawing and according to the programming template in production practice.

Key words：NC turning ; non-circular curve; marco-instruction; programme

0?引言

在數控車削加工中經常會碰到非圓曲線輪廓的工件，所謂非圓曲線輪廓即公式曲線輪廓，其工件輪廓曲線可以用函數公式來描述，比如拋物線、橢圓等。對于這類車削零件在編寫數控加工程序時，如果采用傳統的手工編程方法，其計算的工作量較大、處理的時間較長，并且很容易出現錯誤，難以滿足數控車削加工生產實際的需求。隨著計算機技術的不斷發展，先進的數控系統不斷涌現，為數控編程操作者提供了廣闊的空間，運用宏指令編程是現代數控系統的一個十分重要的新功能，在數控加工領域應用十分廣泛。在各級數控技能大賽和數控操作工技能等級考試中，宏指令編程是主要的考核知識點之一[1]。在企業的生產實踐中，用數控車削機床來加工非圓曲線輪廓的工件時，經常也要用到宏指令編程，然而，許多數控操作工人因為數學基礎較差對數控宏指令編程并不是十分熟悉，對非圓曲線輪廓宏指令編程難以掌握。因此，以基于華中世紀星HNC-21T數控車削系統為例，分析研究車削非圓曲線輪廓宏指令的編程方法、編程步驟，形成公式曲線宏指令編程模板，使數控操作人員在生產實踐中，只要能看懂零件生產圖，根據非圓曲線輪廓宏指令變量編程的步驟，經過簡單的函數公式變形與變換，套用宏指令變量編程模板，就能快速、準確地編寫出復雜工件輪廓的數控加工程序，并能滿足圖紙的加工精度要求，同時結合編程實例，介紹了非圓曲線輪廓宏指令編程模板的具體應用。

1?非圓曲線輪廓宏指令編程方法分析與計算

工件上的非圓曲線輪廓是可以用函數表達式來描述的，如橢圓輪廓用橢圓方程式來描述，通過對函數表達式進行變形與變換，重新確定函數的自變量和因變量;根據曲線輪廓的坐標值來確定函數變量的取值范圍，具體分析與計算過程如下。

1.1?公式曲線函數中自變量確定方法

（1）在華中數控車削編程系統中常用Z坐標來表示軸向尺寸值，用X來表示徑向尺寸值，即直徑值。因此，將公式曲線函數中的兩個變量對應地更換為X和Z，并對公式曲線函數式進行變形與變換，定義其中任意一個變量X或Y作為自變量，其零件的加工效果相同。

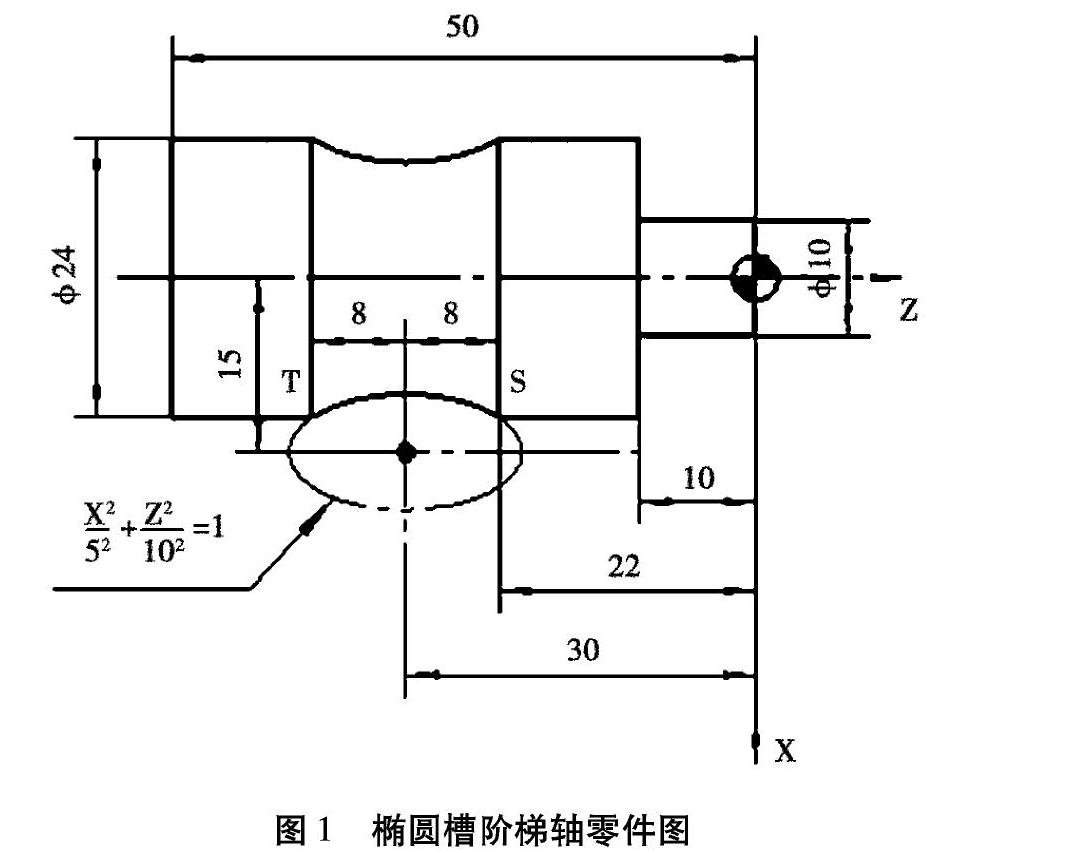
（2）在確定公式曲線函數的自變量時，由于變量范圍越大，可走刀次數越多，零件的加工精度就越高。因此，通常要選擇變量X或Z的變化范圍較大的一個變量作為公式曲線函數的自變量。如圖1所示的橢圓槽階梯軸零件，橢圓槽的輪廓曲線是從起點S到終點T，其變量Z坐標值的變化范圍是0～16 mm，X坐標值的變化范圍從圖中明顯可以看出比Z坐標值的變化范圍要小得多，因此，取變化范圍較大的Z坐標作為該公式曲線函數的自變量比選定變化范圍較小的X坐標作為自變量更合適，加工精度更高。在企業的生產實踐中設計資料證明，由于軸類零件的長度尺寸一般均大于徑向尺寸，所以軸類零件常常選定Z坐標作為公式曲線函數自變量。

（3）根據公式曲線函數表達式在變換或計算時的簡便情況來決定選擇X或Z作為自變量。在圖3所示的三次方函數非圓曲線輪廓零件圖中，其非圓曲線輪廓的函數表達式為

Z=0.005X3（1）

式（1）中含有變量X的多次方，如果我們將變量Z坐標定義為自變量，則關于Z坐標自變量的公式函數表達式變換為

X=3Z0.005（2）

這不難看出式（2）中含X有三次開方函數，使得在采用宏指令編程時不便于用宏指令來表達，因此，如將X坐標定義為自變量則比較合適，同時也方便程序的表達與計算。

（4）華中世紀星HNC-21T數控車削系統變量表示形式為#號后面跟1～4位數字，其中，#0～#49是宏程序中使用的局部變量，常用于存放宏程序中的坐標數據，斷電時丟失為空。為了清楚和方便表達X和Z坐標變量，在這里將與X坐標相關的函數變量設為以#1開頭的數據形式，例如：#1、#11、#12、#13等變量，同時將與Z坐標相關的函數變量設為以#2開頭的數據形式，例如：#2、#21、#22、#23等變量。在生產實踐中，其宏變量的定義也可以完全根據數控程序員或操作工人的習慣來進行定義，不會影響數控加工的質量和效果[2]。

1.2?確定函數中自變量的起始點和終止點的坐標值

公式曲線函數圖像均有自身的平面坐標系，自變量的起始點和終止點的坐標值就是相對于函數圖像自身坐標系的坐標值。這里起始點的坐標值為公式曲線函數自變量的初始值，終止點的坐標為公式曲線函數自變量的終止值，這些坐標值都是結合零件實際輪廓與函數圖像來計算的。在圖1所示的橢圓槽階梯軸零件中，首先確定橢圓線段的Z向坐標為自變量（#2），橢圓曲線起始點S相對于自身的坐標系的Z向坐標值為Z1=+8 mm，橢圓曲線輪廓實際的終止點T的Z向坐標值為Z2=-8 mm。所以公式曲線函數自變量#2的初始值為+8 mm，終止值為-8 mm。在如圖2所示的拋物線非圓曲線輪廓零件圖中，首先確定拋物線段的Z向坐標作為公式曲線函數的自變量，仍用宏變量#2表示，不難看出起始點S的Z向坐標值是Z1=25.626-10=15.626 mm，終止點T的Z向坐標值是Z2=25.626-10-14.026=1.6 mm。因此自變量#2相對于函數自身坐標系的初始值為15.626 mm，終止值為1.6 mm。

在圖3所示的零件圖中，因公式曲線函數表達式中變量X含有三次方，因此選擇X坐標為公式曲線函數的自變量比較合適，計算也較方便，宏變量用#1表示，起始點S相對于函數自身坐標系坐標值

X1=28.171 - 12 = 16.171 mm（3）

終止點T的坐標為

X2=320.005=7.368 mm（4）

因此如式（3）（4）自變量#1的初始值為16.171 mm，終止值為7.368 mm。

1.3?通過函數變換，建立關于宏變量的函數表達式

華中世紀星HNC-21T數控車削系統配備了較強的類似于高級語言的宏程序功能，用戶可以使用宏變量進行算術運算、邏輯運算和函數的混合運算。在圖1所示零件中，公式曲線輪廓函數表達式如果設X坐標為因變量，Z坐標為自變量，則公式曲線函數表達式為式（5）

X=5*SQRT[1-Z*Z/10/10]（5）

根據HNC-21T數控系統宏變量編程表示方法，用宏變量#1表示X，用宏變量#2表示Z，即得公式曲線函數宏變量表達式（6）

#1=5*sqrt[1-#2*#2/10/10]（6）

在如圖2所示零件中，設X坐標為因變量，Z坐標為自變量，則公式曲線函數表達式為式（7）

X=SQRT[Z/0.1]（7）

將X、Z分別用宏變量#1、#2表示，即得#1相對于#2的公式曲線函數宏變量表達式（8）

#1=SQRT[#2/0.1]（8）

在如圖3所示零件中，設Z坐標為因變量，X坐標為自變量，則公式曲線函數表達式為式（9）

Z = 0.005 * X * X * X（9）

根據HNC-21T數控系統宏變量編程表示方法，用宏變量#1表示X，用宏變量#2表示Z，即得公式曲線函數宏變量表達式（10）

#2 = 0.005* #1 * #1 * #1（10）

1.4?確定編程坐標系原點與公式曲線函數自身坐標系原點間的關系

編程坐標系即工件坐標系，公線曲線輪廓是相對于函數自身的坐標系生成的圖像曲線。HNC-21T數控系統宏指令編程必須要明確編程坐標系原點與函數曲線自身坐標系原點的關系，即他們之間在坐標軸上的偏移距離。在如圖1所示的零件中，橢圓曲線自身圖像的原點相對于右端面中心編程原點在X軸方向上的偏移量為ΔX=+15 mm，在Z軸方向上的偏移量為△Z=- 30 mm;如圖2所示的零件圖相關特征為：非圓曲線輪廓函數自身圖像原點相對于右端面中心的編程原點在X軸方向上的偏移量為ΔX=+20 mm，在Z軸方向上的偏移量為△Z=- 25.626 mm。

在如圖3所示的零件中，三次方函數曲線圖像自身坐標原點相對于右端面中心的編程原點在X軸方向上的偏移量為ΔX =+28.171 mm，在Z軸方向上的偏移量為△Z=-9.144 mm。

2?非圓曲線輪廓宏指令編程模板

2.1?將函數中的X作為自變量的宏指令編程通用方法

以X作為自變量，對公式曲線函數表達式進行變換，用宏變量#1替代表達式中的自變量X，用宏變量#2替代表達式中的因變量Z。根據零件加工精度設自變量步長為ΔU，則非圓曲線輪廓段的精加工宏程序編程通用方法如下

#1=X1 （X1是函數自身坐標系下曲線輪廓起始點S的X坐標值，并將該值賦值給自變量#1）

WHILE#1 GE X2（循環條件判斷，X2是函數自身坐標系下曲線輪廓終止點T的X坐標值）

#2=f（#1）（以#1為自變量，#2為因變量，進行函數變換）

#11=±#1+ΔX（#11為編程坐標系下的X坐標值，如編程選用正輪廓，則自變量#1前冠以正，反之冠以負。ΔX為函數自身坐標系原點相對于編程坐標系原點在X軸上的偏移量）

#22=#2+ΔZ（#22為編程坐標系下的Z坐標值，ΔZ為函數自身坐標系原點相對于編程坐標系原點在X軸上的偏移量）

G1 X[2*#11] Z[#22]（G1為直線插補加工指令）

#1=#1-ΔU （自變量#1以步長ΔU作自減運算）

ENDW（結束WHILE循環）

2.2?將函數中的Z作為自變量的宏指令編程通用方法

以Z作為自變量，對公式曲線函數表達式進行變換，用宏變量#2替代表達式中的自變量Z，用宏變量#1替代表達式中的因變量X。根據零件加工精度設自變量步長為ΔW，則非圓曲線輪廓段的精加工宏程序編程通用方法如下：

#2=Z1 （Z1是函數自身坐標系下起曲線輪廓起始點S的Z坐標值，并將該值賦值給自變量#2）

WHILE#2 GE Z2（循環條件判斷，Z2是函數自身坐標系下曲線輪廓終止點T的Z坐標值）

#1=f（#2）（以#2為自變量，#1為因變量，進行函數變換）

#11=±#1+ΔX （#11為編程坐標系下的X坐標值，如編程選用正輪廓，則因變量#1前冠以正，反之冠以負。ΔX為函數自身坐標系原點相對于編程坐標系原點在Z軸上的偏移量）

#22=#2+ΔZ（#22為編程坐標系下的Z坐標值，ΔZ為函數自身坐標系原點相對于編程坐標系原點在Z軸上的偏移量）

G1 X[2*#11] Z[#22] （G1為直線插補加工指令）

#2=#2-ΔW（自變量#2以步長ΔW作自減運算）

ENDW（結束WHILE循環）

3?非圓曲線輪廓宏指令編程模板的具體應用

根據華中世紀星HNC-21T數控車削系統指令格式，運用非圓曲線輪廓宏指令編程模板，結合HNC-21T數控車削系統粗加工循環指令，可以實現公式曲線輪廓的快速、準確編程，具體應用示例如下：

根據圖1所示零件進行工藝分析，設毛坯直徑為25 mm，確定切削參數，則外輪廓的粗加工和精加參考程序如下：

%1（程序頭）

T0101（調用01號車刀，選用01號刀具偏置補償）

G90 M3 S800（絕對坐標編程，機床主軸正轉，轉速800 r·min-1）

G0 X35 Z2 （刀具快速移動到粗車循環指令的起點）

G71 U1 R0.5 P10 Q20 X0.6 F120（G71為粗車循環指令，精車余量為0.6 mm）

N10 G1 X10 F60 S1200（精加工程序的起始段）

Z-10

X24

Z-22 （非圓曲線輪廓的起始點S）

#2=8 （將8賦值給為自變量#2）

WHILE #2 GE [-8]（循環條件判斷，自變量#2的終止值為-8）

（用#1、#2代替函數表達式中的X、Z）

#11=-#1+15（選用負輪廓編程，因些變量#1前冠以負號;ΔX=15）

#22=#2-30 （ΔZ=-30）

G1 X[2*#11] Z[#22] （直線插補加工指令）

#2=#2-0.5（自變量#2以步長0.5作自減運算）

ENDW（循環結束）

N20 G1 Z-50（精加工程序終止段）

G0 X120 Z85（快速定位到退刀點）

M30 （程序結束）

4?結語

宏程序是數控系統的一種特殊功能，它可以實現對零件的復雜形狀或非圓曲線輪廓用簡短的加工程序進行描述，程序具有易讀性和易修改性。運用非圓曲線輪廓宏指令編程模板，只要看懂生產零件圖，直接套用編程模板，就可以快速、準確地編寫出復雜工件輪廓的數控加工程序。數控加工生產實踐證明，不論采用什么方法，在最短的時間內，快速編寫出合格的數控加工程序，并加工出合格的零件，這才是我們所要追求的[3]。

參考文獻：

[1] 禹誠.數控車削加工中公式曲線宏程序編程模板在數控大賽中的應用[J].CAD/CAM與制造業信息化，2007（3）：22-24.

[2] 馬莉.數控車宏程序編程模板的設計及應用[J].科技傳播，2012（5）：25-27.

[3] 馬莉.基于宏程序的橢圓手柄數控編程加工研究[J].湖北農機化，2019（11）：15-17.