基于分組一致性協議的多微網分層優化調度方法研究

國網甘肅省電力公司電力科學研究院 趙龍 張珍珍 丁坤 周強

北方工業大學電氣與控制工程學院 萬慶祝 李俊濤

微網優化調度的方法主要有集中式控制和分布式控制，文獻[1]研究了基于一階離散一致性協議的分布式經濟調度算法，無需中央處理器，即可實現系統的運行成本最小化；文獻[2]分析了儲能單元、柔性負荷參與下的分布式經濟調度控制效果；文獻[3]引入了分布式靜態參數估計方法，加快了基于一致性協議的經濟調度計算速度；文獻[4-5]分別討論了結合下垂控制與經濟調度的直流、交流微電網分布式控制策略。上述文獻所研究算法在微網內任一單元控制量波動時，需要所有智能體參與調節，由于可再生能源發電方式具有隨機性、間歇性，智能體將隨功率的波動而頻繁調節，對系統穩定運行造成隱患。

本文提出一種適用于多微網的分布式優化調度算法。該方法無需中央處理器，僅需有限個鄰居節點間的信息交互。通過分組一致性迭代，既保證了各子微網運行于符合各自需求的控制目標，消除了全局跟隨調節效應，又實現了降低多微網系統運行成本的目的。

1 多微網運行調度模型

針對多微網經濟調度模型，首先計算各子微網的經濟成本，對所有子微網的經濟成本求和，線路損耗可忽略不計，無功功率發電成本不在本文考慮范圍內。

1.1 目標函數

多微網的優化調度需保障系統運行穩定條件下，并使系統總成本在運行周期內最小，即CMGx=min(ΣCx(PG,t)+ΣCx(PL,p)+ΣCx(PB,q))，式中Ctotal、CMGx分別為多微網系統、子微網x的最小運行成本；Cx(PG,t)、Cx(PL,p)和Cx(PL,q)分別為子微網x中第t個可控微源、第p個可控負荷和第q個儲能單元的運行成本。

1.2 成本算式與約束條件

1.2.1 各單元成本

1.2.2 約束條件

等式約束主要考慮區域切分或由多個子微網組成的多微網系統，其內部各子系統的功率平衡。不等式約束主要以各運行單元的輸出或吸收功率上下限為界限。等式約束條件：式中PRG,c為子微網x中第c個可再生能源發電單元輸出有功功率。

不等式約束條件：

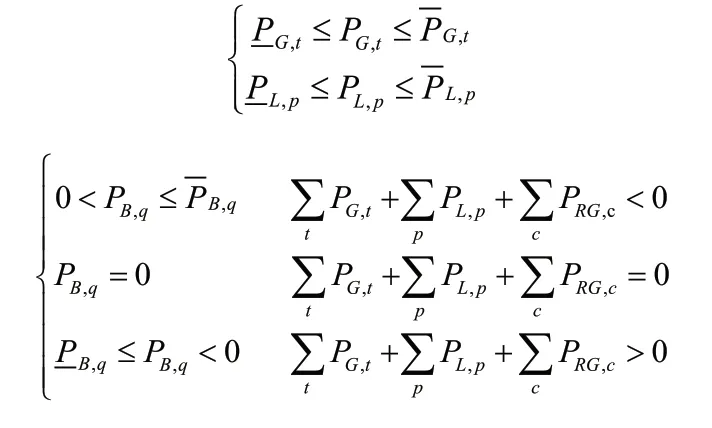
2 基于分組一致性協議的多微網優化調度

2.1 單微網分布式經濟調度算法

基于多智能體系統的分布式經濟調度算法一般以微增率成本為控制量，結合一階離散一致性協議，給出計算方程：

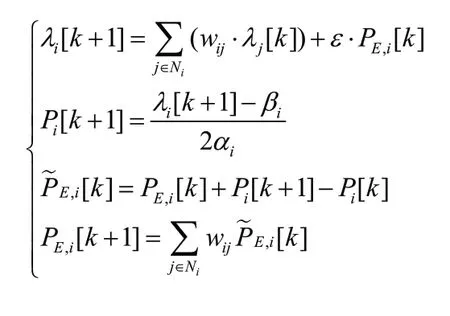
式中λi[k]為可控單元i在第k次迭代時的微增率成本；ε為收斂系數，通過改變收斂系數的取值可以改變系統的收斂效果；PE、i[k]為本地功率誤差估計的第k次迭代值。

2.2 多微網分布式優化調度算法

單微網分布式經濟調度算法無需中央處理器，大大減小系統計算負擔，但系統內部任何一個單元的功率需求變化都要求所有可控單元參與調節，以達到新的平衡狀態。本文所提分組一致性算法各子系統分別實現各子系統的控制目標，而不影響其他子系統的平衡狀態，有利于解決單微網全局跟隨調節問題，因此本文引入分組一致性協議進行多微網優化調度。以微增率成本為控制變量，有式（1）：

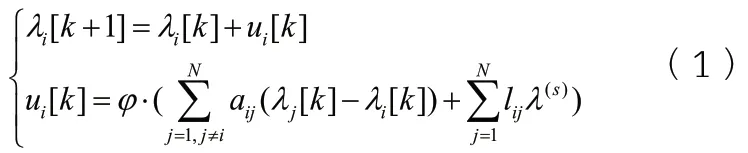
式中λ(s)為子系統s的一致性平均值。

為獲取各子微網的微增率成本一致性平均值，需要設置一個可獲取所有單元控制量初值的中央處理器，這與分布式控制的思想存在矛盾。為此本文采用兩階段計算方式，首先通過單微網分布式調度算法求解各子微網的一致性平均值；其次考慮各子微網間智能體的交互影響，基于分組一致性協議進行各可控單元的微增率成本運算（圖1）。

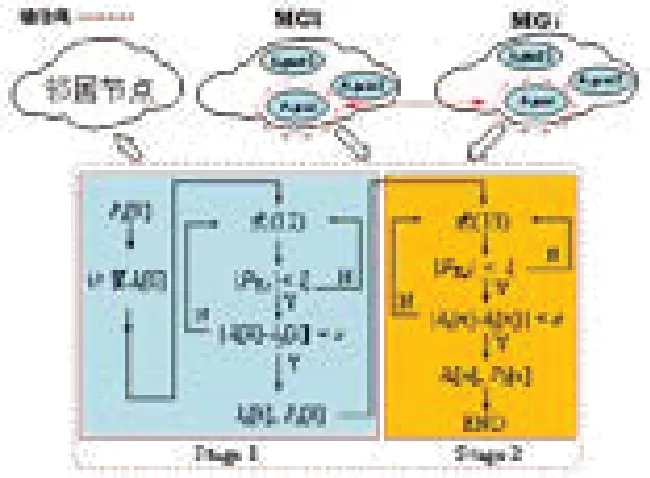
圖1 基于分組一致性協議的多微網分布式優化調度算法

3 仿真分析

3.1 系統結構與參數

本文基于IEEE14節點電氣拓撲結構，構建智能微電網，其中通信拓撲的連接線路與電氣拓撲的連接線路相同（圖2）。

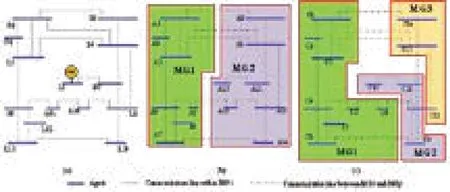
圖2 微電網通信拓撲結構

圖2(a)所示為基于IEEE14節點結構所搭建的單微網通信拓撲。負荷L8所在的母線處，接入了采用最大功率輸出的可再生能源發電單元。圖2(b)和(c)分別為以IEEE14節點為基礎框架的含兩個微電網和含三個微電網的多微網系統。本文假定圖2所示的系統隸屬于同一個利益集體，即多微網的控制目標為在保障各子微網內部供需平衡的前提下實現多微網系統的運行成本最小化。圖2(b)、(c)中，為便于區分，分別采用A和C表示其內部單元。圖2所示的單微網及多微網，系統參數如表1所示。系統參數確定后，基于微增率準則的經濟調度算法，在外界功率需求為零時，可控單元的最優微增率存在且唯一；當外界功率發生波動時，各可控單元微增率將收斂至新的一致性平均值。

3.2 單微網運行

表1 系統參數

以新能源發電單元為功率需求來源，仿真從微增率成本求解精度和迭代次數兩個角度，分析收斂系數的取值對系統收斂效果的作用。

圖3 收斂系數對收斂效果的影響

由圖3可知，功率需求為零時系統的一致性平均值為3.0668。收斂系數在[-10×10-3,0]區間上，收斂系數的增大，使得迭代次數先減小后增大，并且收斂系數取-8×10-3時迭代次數最少。當收斂系數取值在[-10×10-3,-6×10-3]上時微增率收斂值偏離3.0668較遠，而在[-6×10-3,0]區間上計算誤差小于0.001。綜合考慮收斂速度與計算誤差，本文取收斂系數ε=-2×10-3。考慮新能源發電單元出力為零和出力增加至50kW兩種情況，單微網分布式經濟調度算法仿真結果如圖4。

圖4(a)中，新能源發電單元出力為零時，微網內所有可控單元參與調節，最終實現一致性收斂。由圖4(c)和(d)可知，系統達到一致性時，本地功率誤差和系統功率不平衡度均降至0kW。當新能源出力增加至50kW，原有功率平衡被打破，各可控單元在一致性協議的作用下重新進行調節，并達到新的收斂值2.9084，此時各單元的本地功率誤差仍為0kW。

3.3 多微網運行

針對圖2（b）進行仿真如圖5。可知功率需求為零時，MG1和MG2實現一致性，收斂值分別為2.2877和3.9872，實現了多微網系統的經濟調度。

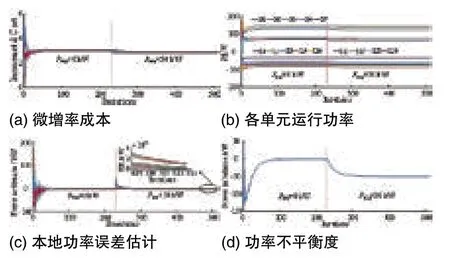
圖4 考慮新能源功率波動的單微網一致性計算結果

圖5 MG1與MG2內部各單元的微增率成本

3.4 運行成本分析

圖6 多微網運行成本

單微網和多微網系統在功率需求為零時的運行成本結果如圖6，可知多微網運行成本為10904.24$，單微網運行成本為27528.42$，多微網運行低于單微網運行成本，隨著微網數量的增加多微網運行成本進一步下降，但成本下降幅度不高。