考慮道路交通狀態的公交運行時間預測
祝佳莉, 陳 鵬, 劉 濱, 池賢昭, 耿小情
(武漢理工大學 交通學院,湖北 武漢 430063)
0 引 言
公交運行時間能夠為乘客出行提供路徑選擇依據,對乘客出行決策而言非常重要。而目前由于交通擁堵等原因,公交運行時間的預測不準確,不光給乘客帶來麻煩,也給公交運營調度、計劃排班等帶來一系列問題。因此建立一種準確的公交運行時間預測模型具有重要的意義。國內外諸多學者對其展開了研究。Teng Jing[1]等基于公交自動定位數據建立預測模型,但沒有考慮道路交通狀態的影響。辛建霞[2]采用歷史數據均值法、時間序列法預測公交路段運行時間,忽略了對運行時間的影響因素的考慮。Marko和Marjan[3]根據歷史數據采用回歸算法預測公交運行時間,雖然預測結果較好,但是預測模型比較復雜。由于公交車運行時間受到實際交通狀況的影響很大,在基于不確定性因素的條件下,任遠等[4]考慮了運行時間的非線性、非高斯特點,采用粒子濾波算法實時預測公交到站時間。陳科宇[5]提出了一種基于支持向量回歸和區間上下界估計方法的公交行程時間預測方法,考慮了公交運行過程中的不確定影響因素,然而該方法只是將點預測值變成預測區間,并沒有將道路交通狀態作為變量進行研究。
公交運行時間的不確定性來源有很多,其中道路交通狀態的變化是導致不確定性的一個重要因素,已有的方法對于公交車運行過程中受到的道路交通狀態影響考慮得較少,缺乏對其指標的深入分析。在考慮以上問題的基礎上,本文提出將前車的速度均值及方差作為道路交通狀態指標,以量化公交在路段上運行過程中道路交通狀態的不確定性,并通過指標相關性分析進行深入研究,在此基礎上構建了隨機森林模型,用以進行公交運行時間預測。
1 道路交通狀態指標選取
1.1 符號表達
為了描述方便,本文中所涉及的字符描述統一如下:
Ω:站點集合。
A,B:站點編號,其中A,B∈Ω,A,B>0,且為整數。
lAB:表示A、B站點之間的路段。
N:公交車集合。
i,k:公交車編號(i,k為自然數),表示公交車到達路段的時間順序;其中i,k∈N,k ti:第i輛車的運行時間(ti>0),s。 Δtk,i:第i輛車與第k輛車的車頭時距,s。 vari:第i輛車的速度方差,km2/h2。 道路交通狀態是指交通運行的整體情況在某一路段或者區域內的客觀表現,在一定程度上可以用來表示道路的擁堵情況[6]。公交車在運行過程中主要受到道路交通狀態的影響,由于其具有隨機性和變化性,如何量化道路交通狀態成為提高公交車到站可靠性的關鍵。 道路交通狀態反映了道路的擁擠程度,而車速會由于擁堵程度而變化,路段越暢通,行車速度越快。參考《城市交通管理評價指標體系》,本文采用前車的車速作為衡量道路交通狀態的指標[7,8]。 如圖1所示,以路段lAB上第i輛公交車為研究對象,第k輛車是在第i輛車之前的某一輛車,假設公交車在路段上不發生串車。 圖1 公交運行過程圖 決策樹[9]是經典的有監督學習方式,由根節點、內部節點和葉子節點三部分組成。決策樹在進行屬性劃分時容易出現過擬合現象,無法很好地在數據上實現泛化,并且對數據的變化很敏感,不夠穩定,無法確保返回全局最優。隨機森林算法[10]是對決策樹算法的改進,通過構建決策樹的時候對數據進行隨機訓練,預測時綜合多棵決策樹的結果,能夠處理高維度的數據,對誤差使用無偏估計,模型泛化能力強,如果有特征遺失,仍可以維持準確度,具有更強的魯棒性。 隨機森林算法可以處理分類問題和回歸問題,因此本文構建隨機森林回歸模型預測公交運行時間,其預測算法流程如圖2所示。 圖2 隨機森林公交運行時間預測算法流程 基于隨機森林的公交運行時間預測算法流程為: (1)從原始數據集D中采用有放回隨機抽樣法抽取λ個子集Di,Di中樣本的容量與D相同。若D中樣本為n,每個樣本被抽取的概率為1/n,循環抽取n次,D中每個樣本抽取的概率為(1-1/n)n,當n足夠大時(1-1/n)n≈0.368,保證了子集樣本的差異性。 (2)假設模型共有M個特征變量,對每個子集Di隨機抽取m個特征,根據基尼系數重復選擇決策樹最優特征用于分裂節點,直到基尼系數小于設置的閾值,此時生成一棵分類回歸樹。 (3)每一棵決策樹得到一個公交運行時間預測值,計算λ個預測結果的均值作為最后的預測結果,計算公式為: (1) 式中:λ表示隨機森林中決策樹的個數,Ti(x)表示第i棵決策樹預測的公交運行時間。 本文以MSE(mean square error,均方誤差)和MAPE(mean absolute percentage error,平均絕對百分比誤差)作為模型的性能評價指標,其計算公式分別為: (2) (3) 本文選取了天津市35路公交的自天塔南至東風里路段2017年10月8-24日的公交數據為實驗對象,共800個樣本。在進行研究之前需要對原始數據進行預處理,去除對于GPS數據偏離較大的點,對于缺失數據,采用插值填補,將前后兩個數據的平均值作為插入數值。以二進制“0”和“1”表示事件發生有無標記高峰和周末。經過處理后得到的預測模型輸入數據見表1。選取10月8-22日的700個數據作為公交運行時間預測的學習模型,10月23-24日的100個數據用于分析預測模型的性能。 表1 預測模型輸入數據 由于目標車輛i與前車之間有一定的時間間隔,時間間隔的取值決定了用前車的速度作為衡量指標的效果。若取值過大,雖可以有效地定性分析交通狀態,但無法反映其時變特征,若取值過小則會導致計算量增大,判別效率低下[11,12]。因此在進行指標選取之前需要分析前后車的車頭時距是否滿足標準。 通過隨機選取路段上車頭時距(圖3)進行統計分析可知,Δti-1,i的分布基本符合均值為254、方差為59.7的高斯分布,Δti-1,i落在3~7 min范圍內的有91%,Δti-2,i也基本上在6~15 min范圍內,滿足3 min≤Δtk,i≤15 min的要求[13]。因此可以將前面兩輛車的速度均值、方差作為衡量目標車輛運行時道路交通狀態的指標。 圖3 車頭時距分布圖 本文采用隨機森林回歸模型進行公交運行時間預測,為保證預測模型的精度,首先需要對指標進行多重共線性判斷,選取有效的預測模型輸入變量。一般可以采用Pearson相關系數來篩選存在共線性的變量。兩個變量之間的Pearson相關系數定義為它們的協方差和標準差的商,計算公式為: (4) 計算自變量兩兩之間的相關系數及自變量與因變量之間的相關系數,當自變量之間的相關系數大于0.7,且自變量與因變量的相關系數小于0.05時,則可以認為自變量之間存在共線性,反之可認為不存在共線性。相關性分析結果如圖4所示。 圖4 共線性判斷 圖4中,公交運行時間預測模型的輸入變量為前車的速度均值、前車的速度方差、前車的運行時間、前車的車頭時距、高峰與否、周末與否。從圖4中可以看出自變量之間的Pearson相關系數均小于0.7,可認為自變量之間不存在共線性。 在隨機森林算法中,決策樹的數量和每棵樹使用的最大特征數是兩個關鍵參數,構建公交運行時間預測模型的關鍵是確定這兩個參數的取值。隨機森林允許單個決策樹使用特征的最大數量,因此將該值設置為9。決策樹的數量通過試驗來決定,試驗發現當決策樹數量大于100時模型的誤差基本穩定,因此在保證模型精度的條件下,本次實驗將決策樹的數量設置在200。 為分析隨機森林預測模型的性能,本文選取了在回歸預測方面適用性較廣泛的人工神經網絡[14](artificial neutral network,ANN)作為對比。構建單層的ANN預測模型,隱藏單元設置為4個。 將考慮道路交通指標與不考慮道路交通指標的隨機森林模型進行對比,結果如圖5所示。對比兩個模型誤差,增加了本文所提出的指標之后,考慮道路交通指標模型的MSE降低了42.71 s2,平均絕對百分比誤差降低了15.44%,選取的道路交通狀態指標提高了公交運行時間預測模型的精度。 圖5 不同指標間的隨機森林預測結果曲線圖 同時在考慮道路交通狀態指標的基礎上,構建了隨機森林和ANN預測模型進行對比,如圖6所示。 圖6 ANN與隨機森林模型預測結果曲線圖 由圖6可知,隨機森林模型預測曲線更加能夠反映公交運行時間的變化趨勢,擬合效果更好。對比模型的均方誤差和平均絕對百分比誤差(表2),隨機森林模型的MSE為43.66 s2,相較于ANN誤差降低了36.15 s2;MAPE為11.66%,相比于ANN,預測精度提高了11.91%。兩個指標都說明基于隨機森林的公交運行時間預測模型優于ANN。 表2 模型的預測性能比較 本文在提出將前車的速度均值和方差作為目標車輛的道路交通狀態指標的基礎上,構建了基于隨機森林的公交運行時間預測模型。通過天津市35路公交的自天塔南至東風里路段2017年10月8-24日的公交數據進行實例分析,得出以下的結論: (1)前車的速度均值和方差能夠作為目標車輛的道路交通狀態指標,將其作為公交運行時間的輸入變量后對預測模型的精度有很大的改善。 (2)基于隨機森林的公交運行時間預測模型比基于人工神經網絡的公交運行時間預測模型精度更高,并且參數較少,操作簡單,能夠為高精度的運行時間預測提供參考。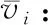
1.2 指標選取


2 公交運行時間預測模型




3 實例分析
3.1 數據采集與處理

3.2 指標合理性分析

3.3 輸入變量的選取


3.4 參數設置
3.5 結果比較



4 結 論

