簡支轉連續橋的動載測試分析及數值模擬
肖 波, 黃 禹
(武漢理工大學 交通學院,湖北 武漢 430063)
0 前 言
隨著交通運輸行業的發展,橋梁荷載的等級也隨之增加,現有的部分橋梁已無法滿足交通運輸行業發展的需要,加之車流量的急劇增加以及嚴重的車輛超載現象,給公路橋梁帶來了較嚴重的損傷,使得橋梁的使用年限大大縮短[1]。部分既有橋梁由于惡劣的運營環境,長期受到酸堿鹽腐蝕和凍融循環等因素的影響,橋梁耐久性降低,已經不能提供安全使用的能力[2]。因此,通過對仍具有一定可利用價值的公路橋梁進行檢測、評估,應用一定的技術手段對其加固,以達到提升性能,減少資源浪費,節約大量資力,具有較高的技術經濟價值和社會價值。
簡支轉連續橋梁結構是兩跨及兩跨以上的預應力混凝土梁架設在支座上,通過現澆混凝土并張拉預應力鋼束形成的連續結構體系。對比簡支梁橋而言,簡支轉連續梁橋具有剛度大、變形小、伸縮縫少和行車舒適等優點[3];預制的簡支梁的預應力鋼束在工廠進行張拉,當轉為連續結構體系時在負彎矩區的預應力鋼束布置及張拉均可以在梁上進行,避免了因施工過程對橋下船只運行或車流的影響[4]。簡支變連續梁橋,能增強橋梁整體結構的穩定性,而且使行車更舒適;尤其是對于橋墩高度比較高、橋墩高度相差懸殊大、橋上縱坡比較大的橋梁,做成多孔簡支變連續,有利于橋梁的整體穩定以及橋墩能均衡受力,而且使梁受力明確,消除單跨不均衡受力狀態[5]。由于簡支轉連續梁橋中在現澆混凝土中存在著結構體系轉換過程,橋梁的實際受力情況存在著不準確性,因此需要對橋梁進行動載測試及動力響應分析。
1 橋梁自由振動理論分析
將試驗橋梁簡化為Euler-Bernoulli梁研究橋在自由振動下的自振模型表達,試驗橋梁的主要參數用如下的符號表示:EI(x)為梁單位長度下的剛度,m(x)為梁單位長度下的質量,對于等截面勻質梁EI(x)、m(x)為常量EI、m,y(x,t)為梁截面任意位置在某一時刻t的豎向撓度,豎向荷載p(x,t)、剪力Q(x,t)隨著荷載位置x和時間t變化。
根據牛頓第二運動定律,建立運動方程:
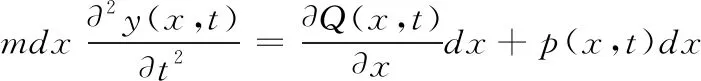
(1)
根據材料力學公式

(2)

(3)
式中:M(x,t)為距離梁左端x截面處的彎矩。將式(2)、式(3)代入式(1),得

(4)
當梁處于自由振動時,此時沒有外力作用于梁上,將p(x,t)=0代入式(4),梁的運動微分方程化為:

(5)
運用分離變量法,將豎向撓度y(x,t)分解為:
y(x,t)=Y(x)T(t)
(6)
將式(6)代入式(5)中得:

(7)
變化式(7)得:

(8)
則w2為x和t無關,w2為常數,式(8)左側可得:
(9)

(10)
則T(t)、Y(x)的通解為:

(11)
Y(x)=A1sinβx+A2cosβx+A3shβx+A4chβx
(12)
第i階結構的自振頻率為:

(13)
橋梁的自由振動函數可以寫為各階主振型函數的疊加,其中wi為梁的第i階自振頻率,則梁的自由振動函數為:
(A1isinβix+A2icosβix+A3ishβix+A4ichβix)}
(14)
2 工程概況
某橋上部結構采用5×30 m+6×30 m+5×30 m預應力簡支變連續T梁橋,橋梁為左右獨立的兩幅橋,橋梁單寬:0.5 m(防撞護欄)+14.75 m(行車道)+0.5 m(防撞護欄)=15.75 m,全橋為雙幅橋,兩幅橋中間寬0.5 m,整幅橋寬32 m,設計洪水頻率為1/100,橋面橫坡為行車道2%,地震動峰值加速度系數0.05,選取該橋左幅第一聯作為實驗跨,如圖1所示。

圖1 實驗跨橋跨布置圖
3 有限元模擬及振型分析
通過有限元軟件MIDAS Civil建立實驗跨的有限元模型,采用梁格法對結構進行計算分析,共建立1 057個節點,1 956個單元。橋梁左幅第一聯成橋階段模型如圖2所示。

圖2 左幅第一聯成橋階段橋梁模型
根據橋梁的實際情況計算橋梁的前三階模態及對應的振型,表1給出了MIDAS有限元計算得到的橋梁固有頻率及對應的基本自振周期,圖3為橋梁的前三階振型圖。

表1 橋梁固有頻率及周期計算結果

圖3 橋梁的前三階對應振型圖
4 橋梁的動載試驗
車輛荷載在橋面行駛時對橋梁結構有沖擊和振動作用,主要分為兩部分,第一部分是車在橋面上時車輛與橋梁組成車橋聯合振動體系,第二部分是在車輛駛出橋面后橋梁結構自身的自由衰減振動。有障礙行車試驗在橋面跨中設置高度為6 cm的弓形木板,一輛400 kN載重車以20 km/h的速度勻速駛過橋面,測定橋梁在車輛荷載作用下的強迫振動響應及振動衰減過程[6]。試驗載重車示意圖如圖4所示。主要技術指標為:前軸1距前軸2為1.4 m;前軸2距中軸為4.5 m;中軸距后軸為1.9 m。

圖4 加載汽車軸載、尺寸示意圖
試驗跨有障礙行車試驗的豎向加速度時程響應曲線如圖5所示。
橋梁動載試驗采用高靈敏度隨機信號與振動分析系統、傳感器和放大器以及濾波器,測量由試驗車所引起的橋梁微小且不規則的振動,通過放大器和濾波器對數據進行采集,并進行譜分析,最終得到橋梁結構的動力特性。實際數據采集在橋梁的第二跨跨中附近設1個豎向振動測點,以測量在脈動工況下的豎向加速度響應信號。測量結果如圖6所示。

圖6 試驗跨豎向加速度響應譜圖
由加速度的響應譜圖可以看出,實測試驗跨的一階固有頻率為4.75 Hz,大于MIDAS試驗跨有限元模型一階自振頻率的計算值,說明了橋梁的整體剛度滿足承載力要求。
5 結束語
在預應力混凝土連續梁橋的承載力評估過程中,橋梁的動載試驗是必不可少的。通過建立橋梁的自由振動的理論模型,結合橋梁脈沖試驗及橋梁的動載試驗得到橋梁的固有頻率及豎向加速度響應曲線,這對橋梁動力參數進行檢測及橋梁的損傷識別及養護加固措施有理論的指導意義,同時也說明了橋梁動載試驗的可靠性,為今后預應力混凝土連續梁橋的橋梁試驗提供了參考。

