基于五階容積-二階平滑變結構濾波算法的捷聯慣導系統初始對準技術

陳 帥，王婉晨，王逸辰，朱 瑋

（1.遼寧石油化工大學信息與控制工程學院，撫順 113001；2.北京航天控制儀器研究所， 北京 100039）

0 引言

捷聯慣導系統因其自主性強、隱蔽性好、抗干擾能力強以及其全信息服務等優點被廣泛應用于航空、航天、航海等各個領域［1］。初始對準技術是捷聯慣導系統的關鍵技術之一，用于求解慣導系統導航解算過程所需的初始方向余弦矩陣。初始方向余弦矩陣是由初始對準過程得到的初始姿態角和方位角確定的，初始對準過程的時間和對準結果的精度是影響后續導航解算過程的兩個非常重要的因素。然而，初始對準時間的減小與對準精度的提高兩者之間是矛盾的關系。在一般情況下，初始對準時間越長，初始對準結果的精度才會越高。為了解決這一矛盾，很多學者對此進行了不同方式與方法的改進研究。

為了提高初始對準過程中方位失準角的收斂速度，文獻［2］提出了一種快速初始對準方法，該方法采用水平失準角的估計值來計算方位失準角。而為了增加初始對準過程的對準精度，文獻［3］建立了東向陀螺漂移的估計模型用于補償方位失準角的估計精度。但是，這兩種方法都依賴于低通濾波器的設計與使用，方位失準角的估計結果對慣性傳感器的噪聲很敏感［4］。為了解決慣性傳感器的未知噪聲特性和穩定性問題，很多學者對此做了大量的研究工作，提出了很多新穎的濾波算法，如KF/UPF［5］、CKF［6］、五階CKF［7］等。即便如此，在精對準過程當中，假設量測噪聲滿足量測噪聲和過程噪聲方差值已知的Gauss分布，那么Kalman濾波方法始終是最優的線性估計器［8］。

然而，Kalman濾波對準方法是一種線性濾波方法，其不適用于非線性初始對準過程。二階平滑變結構濾波方法是一種不需要誤差協方差矩陣的預測—校正估計方法［9］，其能夠克服噪聲和干擾影響，是一種簡單且實用的魯棒濾波方法。為了改善捷聯慣導系統初始對準過程中方位失準角的對準精度，本文提出了一種基于組合對準結構的二階平滑變結構濾波對準方法。該組合對準結構將Kalman濾波對準方法和羅經對準方法相結合，構建了一個狀態變量與量測變量維數完全相同的初始對準模型，由二階SVSF來完成對此組合對準模型的狀態估計過程。實驗仿真結果表明，該方法對準得到的方位失準角對準結果優于一些目前較為常見的初始對準方法。

1 組合對準模型

1.1 誤差傳遞模型

在大方位失準角的非線性模型中，方位失準角的估計誤差仍舊是影響導航精度的主要因素。因此，為了改進精對準過程中失準角的估計性能，本文采用了基于Kalman濾波對準方法的非線性誤差傳遞模型。選取當地的東北天坐標系作為導航坐標系，即n系［10］。在n系中，大方位失準角和速度誤差方程表示如下

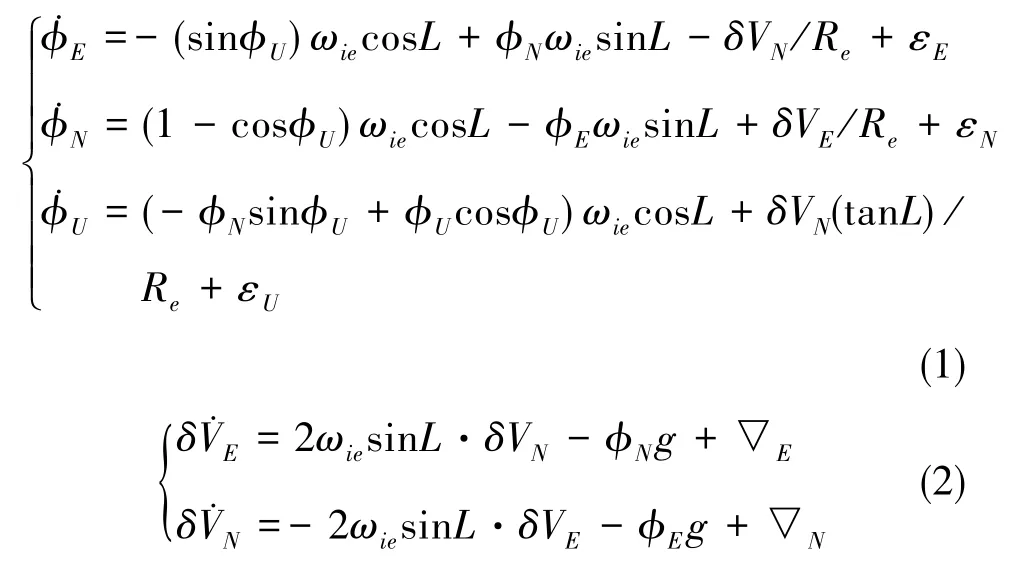
式（1）和式（2）中，φE、φN和φU分別為俯仰失準角、橫滾失準角和方位失準角；ωie為地球自轉速率；ε和▽為陀螺的常值漂移率和加速度計的常值零偏，下標E、N和U分別代表n系的東北天三個軸的指向；δV為速度誤差；g為當地的重力加速度；L為當地的緯度；Re為地球的半徑。

為了縮減狀態變量、增加量測變量從而使狀態變量維數與量測變量維數得到統一，本文實際采用的非線性對準模型為上述對準模型的降階形式，僅失準角和速度誤差作為狀態變量，由其構成的狀態方程表示如下

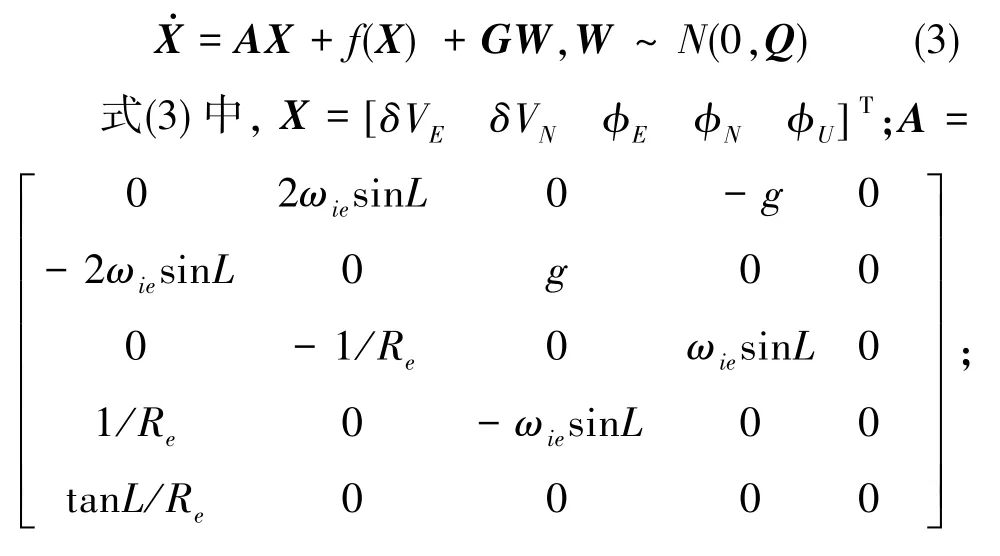
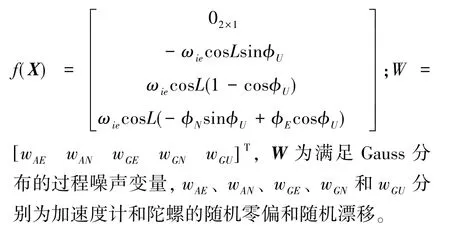
常見的初始對準過程中的零速量測模型表示如下

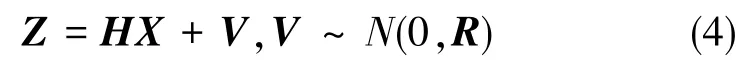
式（4）中，Z＝［δVEδVN］T；V＝［vEvN］T，V為滿足Gauss分布的量測噪聲變量，vE和vN分別為東向和北向速度變量的隨機誤差；H＝［I2×2O2×3］為量測轉移矩陣。

1.2 羅經對準方法

為了改善一定時間區間內的對準精度，本文采用了變參數羅經對準方法。在靜基座的情況下，姿態方程和速度方程可以表示為

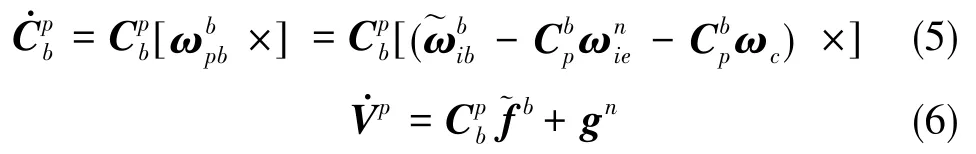
水平羅經環路和方位羅經環路的示意圖分別如圖1和圖2所示。

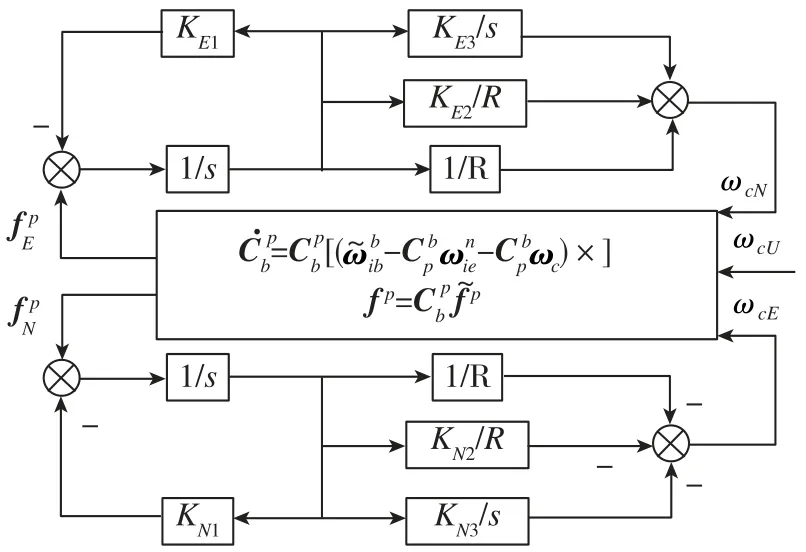
圖1 水平羅經環路示意圖Fig.1 Diagram of horizontal compass loop

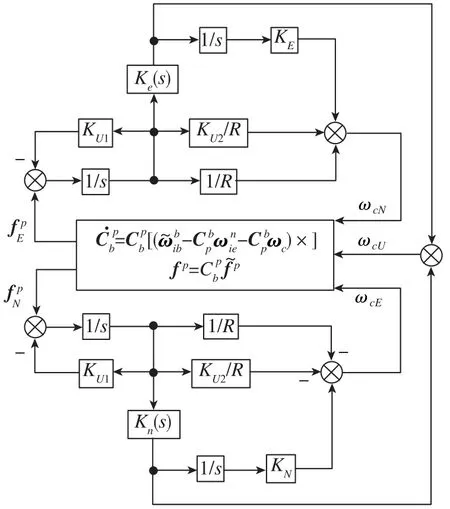
圖2 方位羅經環路示意圖Fig.2 Diagram of azimuth compass loop

由圖1和圖2可知，變量KEi、KNi和KUj（i＝1，2，3；j＝1，2，3，4）是控制參數，其值可通過式（7）、式（8）計算得到

式（9）中，HE＝HN＝1，東向速度誤差和北向速度誤差同時用于計算方位軸的控制角速率，這樣圖2才能夠用于大方位失準角的對準過程。為了縮短對準過程的收斂時間，方位對準環路中需采用一種變參數方法，即

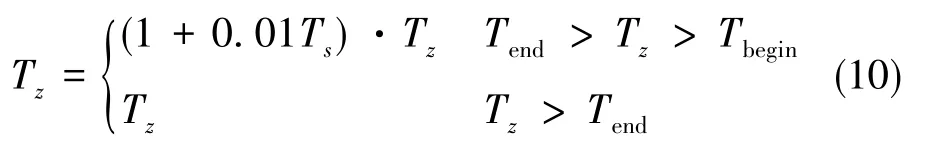
式（10）中，Tbegin為方位羅經對準的起始時間，Tend為確保方位對準角收斂到小角時所需的最長時間節點。當Tz＞Tend時，控制參數Ke（s）為零。

1.3 組合對準機制示意圖

在捷聯慣導系統的初始對準過程中，系統是不完全可觀和可控的，因為Kalman濾波方法不能夠準確估計慣性傳感器的常值漂移，這也就導致了失準角會存在一定的理論誤差值。通常，這些傳感器的常值漂移可以通過旋轉調制技術進行一定的補償，但旋轉調制技術的引入會加大慣導系統的復雜度，而且會引入額外的誤差。為了簡化系統的復雜程度，減少額外誤差的引入，本文提出了一種組合對準方法用于解決因慣導系統不完全可觀可控而導致的狀態變量可觀測度低的問題。該方法在羅經對準進入理論誤差范圍內后將Kalman濾波模型中的速度量測模型切換到組合過程中的增量模型，該增量模型的量測狀態由速度誤差、姿態角誤差和方位角誤差構成。

為了實現這一組合對準過程，有兩點是需要明確知道的。第一點就是增量量測模型的建立是為了實現完全可觀測模型的構建，增量量測模型采用三個失準角和水平速度誤差作為量測狀態，從而構成了五維量測模型。其中，三個失準角可以通過在同一時間節點下求得的Kalman濾波方法中未補償的方向余弦矩陣與羅經對準方法中補償后的方向余弦矩陣乘積并求解得到。失準角的計算過程可以按式（11）和式（12）來進行求解

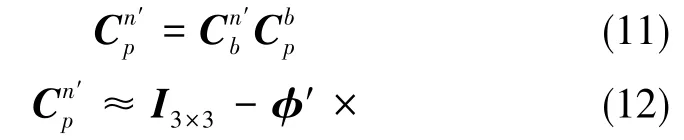
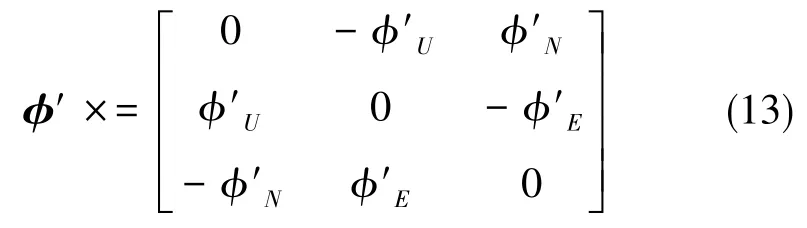
因此，增量量測模型可以用式（14）來表示

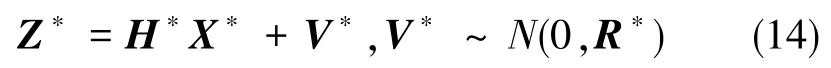
式（14）中，Z?＝［δVEδVNφ′Eφ′Nφ′U］T，V?＝［vEvN0 0 0］T，H?為一個5×5的單位矩陣。所以，由式（5）和式（14）便可構成完全可觀測的組合對準模型。由于在大方位失準角對準過程中，方位失準角不能同小失準角一樣進行線性等效，因而需要通過姿態矩陣來進行姿態的計算。

實現組合過程的第二點就是切換時間的選擇。Kalman濾波對準方法收斂到理論精度的速度要比羅經對準方法快，為了得到更加準確的量測值就需要選擇羅經對準結果進入理論精度區域后的時間作為兩種方法的組合時間。組合對準機制流程圖如圖3所示。

在圖3中，Kalman濾波對準方法和羅經對準方法同時運行。t1為水平角對準時間，t2與t3之和為方位角對準時間。t2時間段為方位角穩定階段，即羅經對準結果收斂到理論精度范圍內的階段。在方位角穩定之后，式（4）切換到式（14），由式（3）和式（14）來完成后續的組合對準過程。

因為兩種對準方法的方位失準角的理論精度計算不盡相同，作為量測狀態變量的方位失準角誤差與狀態變量的方位失準角誤差在組合過程中會部分抵消。因此，組合對準得到的方位失準角估計值略優于常規對準方法。

2 五階容積-二階平滑變結構方法

二階平滑變結構濾波方法在其預測更新過程中是一個預測-校正的形式。在預測過程中，先驗狀態估計通過k時刻的系統先驗知識來進行計算。在更新過程中，計算得到的先驗估計值用來產生后驗狀態估計值。在這種方法中，校正增益用于將估計的狀態和其一階導數限制在滑動超平面的臨近區域，這個臨近區域也就是其存在子空間。為了便于描述二階平滑變結構濾波過程，假設通過離散時間狀態轉移模型表示的一類非線性系統為

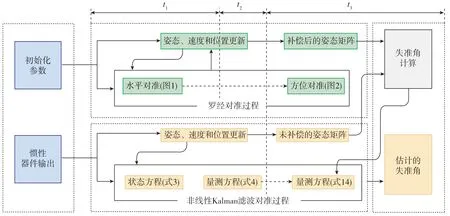
圖3 組合對準過程示意圖Fig.3 Schematic diagram of integrated alignment process

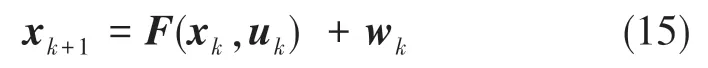
式（15）中，F：Rn+p→Rn為非線性狀態轉移函數，xk+1∈Rn×1為狀態變量，uk∈Rp×1為控制變量，wk∈Rn×1為過程不確定變量。假設量測方程為線性或分段線性的，那么其可具體表示如下

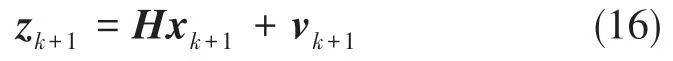
式（16）中，zk+1∈Rm×1為量測變量，vk+1∈Rm×1為量測噪聲，H∈Rm×n為一個已知的正對角線或偽對角線測量矩陣。

二階平滑變結構濾波算法是針對線性系統進行設計的，為了解決該系統的非線性問題，本文提出采用五階容積規則進行一步預測，從而構建成了五階容積-二階平滑變結構濾波算法，該算法在非線性系統中的應用主要可歸納為以下5個步驟［10］：

1）由系統的狀態轉移矩陣得到的先驗狀態估計向量的預測為

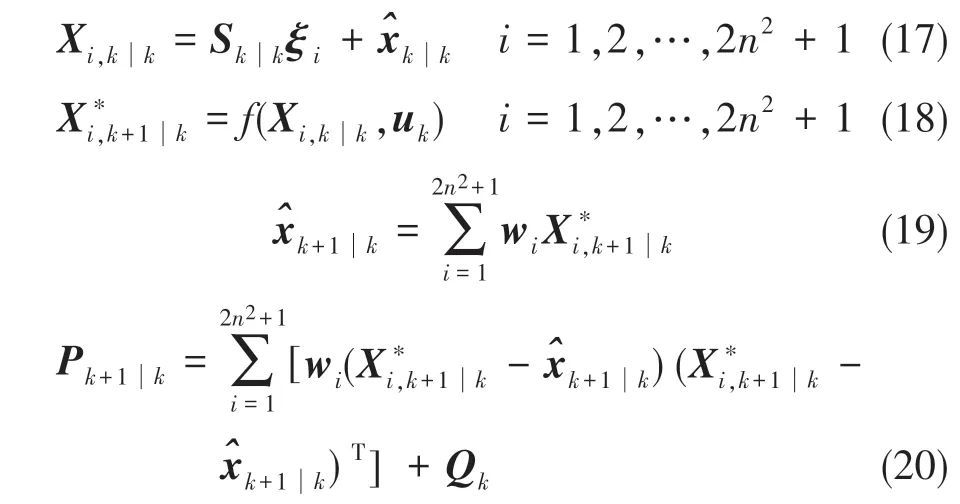
其中，容積點和權重表示如下

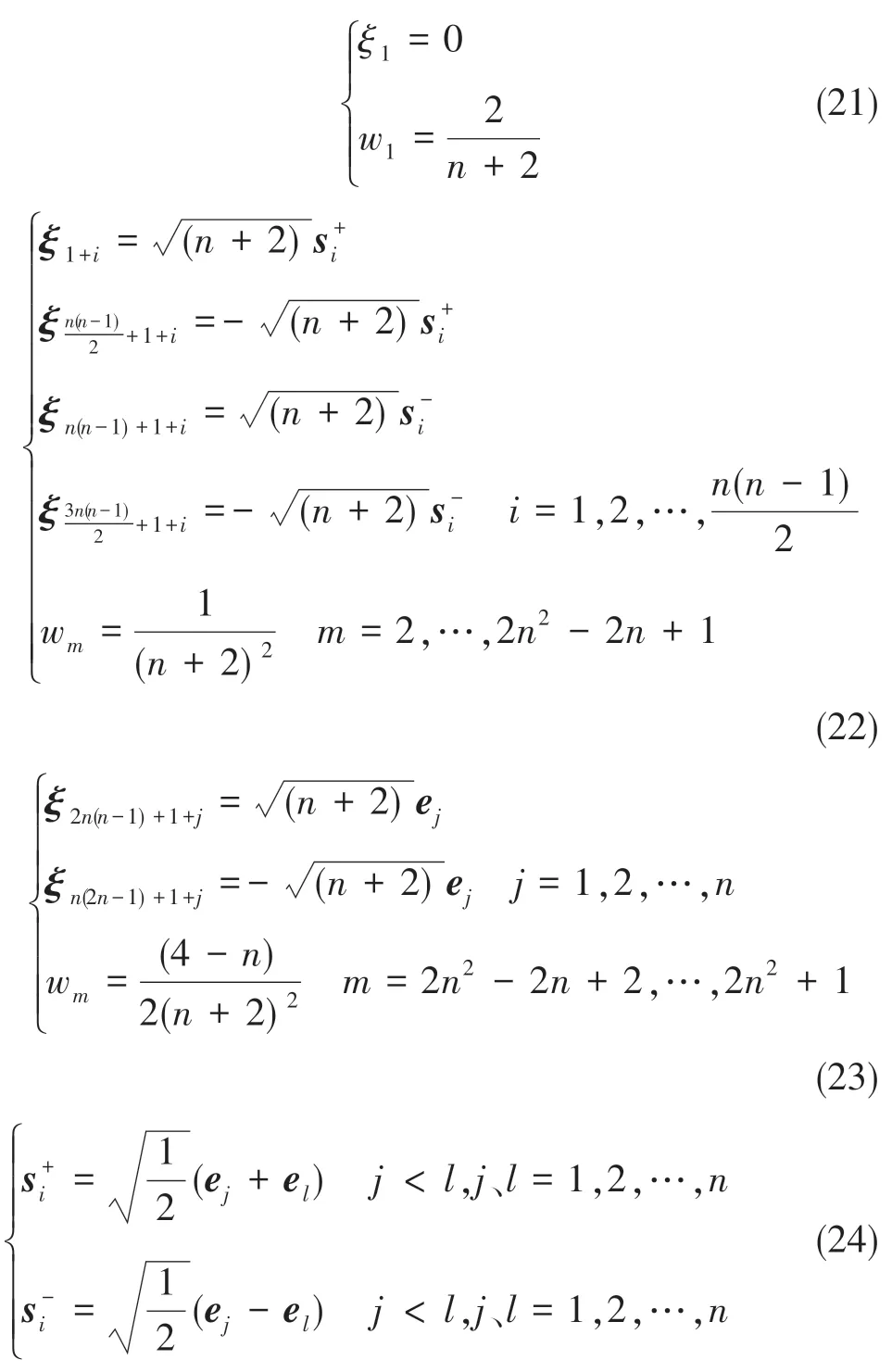
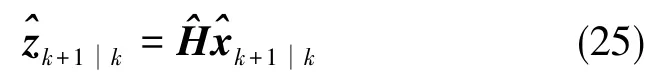
式（25）中，為準確的量測模型H的估計。

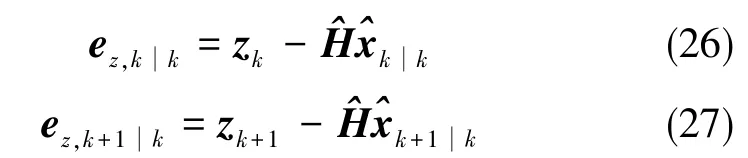
3）二階平滑變結構濾波算法校正增益向量Kk+1∈Rn×1可通過一個包含了先驗量測誤差、后驗量測誤差和前一時刻的后驗量測誤差的函數來表示

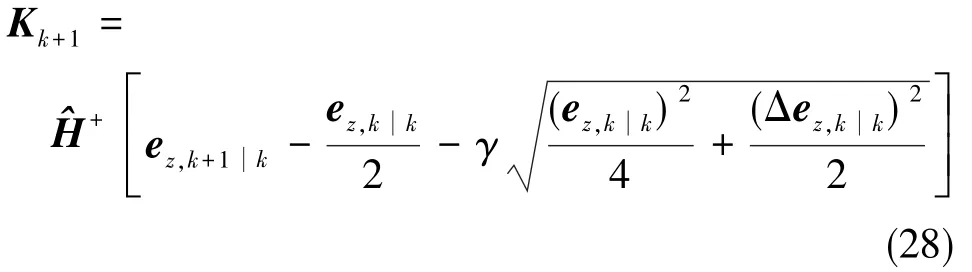
式（28）中，為量測矩陣的偽逆。假設初始時刻所有狀態是可測的，那么和H在初始時刻就是方陣，。γ＝diag（γii）∈Rm×m為一個對角矩陣，其對角元素滿足0＜γii＜1。

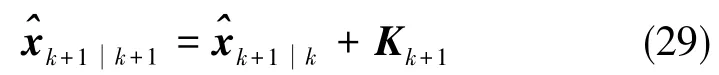
5）在每個采樣時間點進行步驟1～步驟4的迭代重復就是整個算法的具體實現過程，需要特別說明的是后續的迭代過程中，需要將作為來使用。

3 仿真驗證

3.1 仿真參數

初始對準過程的仿真參數如表1所示。一般地，大方位失準角不會超過15°，因此將初始方位失準角設為15°，水平失準角設為1°。

常規非線性Kalman濾波方法（UKF、CKF和五階CKF）的初始參數如下所示：

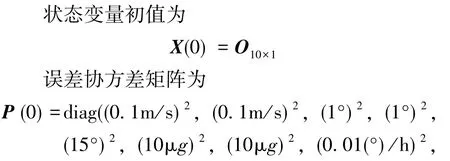
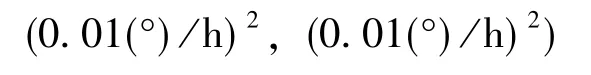
表1 仿真參數Table 1 Simulation parameters

五階容積-二階平滑變結構濾波算法的初始參數表示如下：

3.2 仿真結果與分析

仿真過程持續600s，五階容積-二階平滑變結構濾波算法可以通過圖3中的組合對準方法來實現。組合對準過程開始于200s之后，失準角誤差曲線如圖4～圖6所示。

在圖4中，很明顯俯仰失準角誤差不是最小的，但卻是穩定的。同樣的現象在圖6中也可以看到，而且在所有估計方法中，其方位失準角誤差是最小的，方位失準角誤差是精對準過程的關鍵。因此，五階容積-二階平滑變結構濾波對準方法能夠較好地解決大方位失準角對準問題。

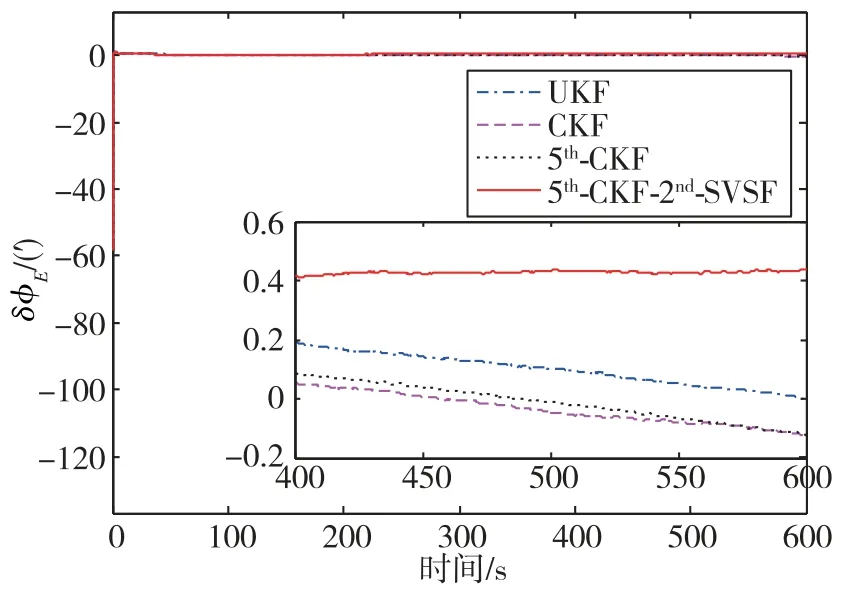
圖4 俯仰失準角估計誤差曲線Fig.4 Estimation error curves of pitch misalignment angle

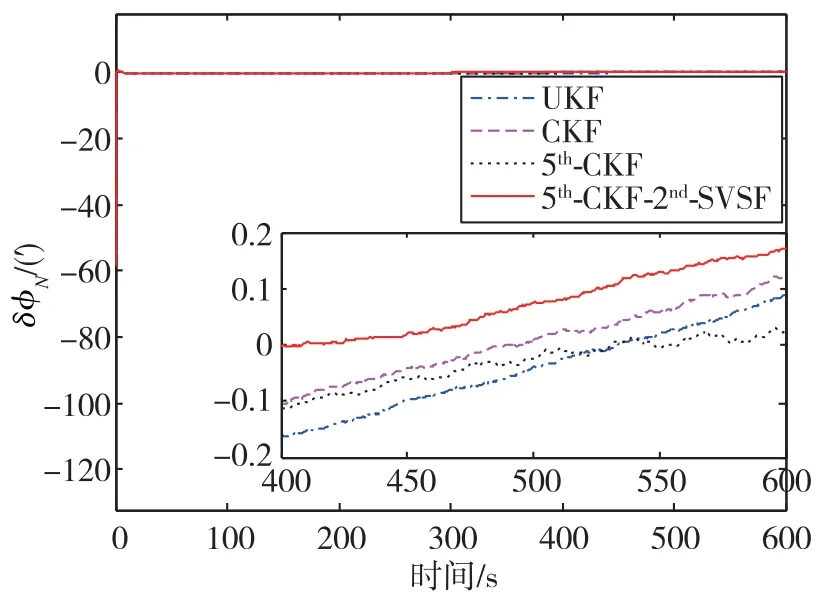
圖5 橫滾失準角估計誤差曲線Fig.5 Estimation error curves of roll misalignment angle

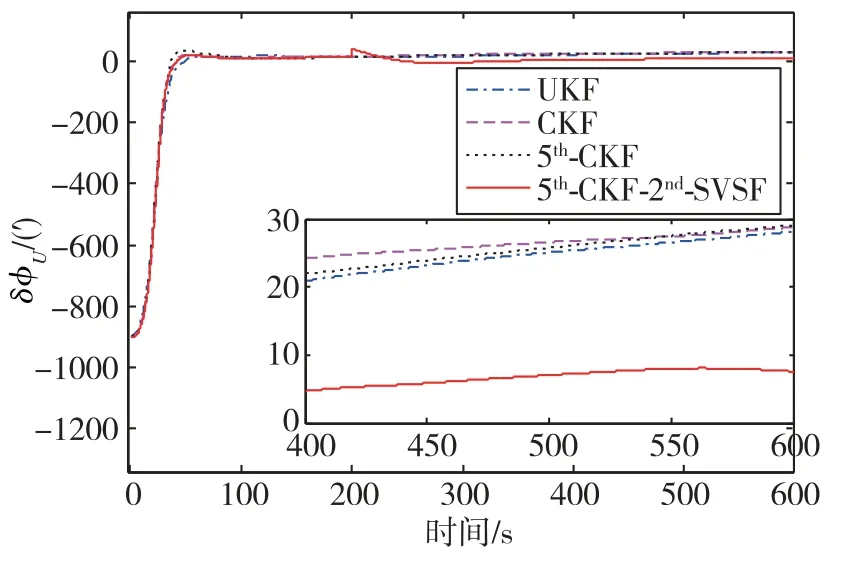
圖6 方位失準角估計誤差曲線Fig.6 Estimation error curves of azimuth misalignment angle

為了表明五階容積-二階平滑變結構濾波算法的有效性，在誤差測量條件下進行了100次Monte Carlo仿真模擬，均值和標準差如表2和表3所示。

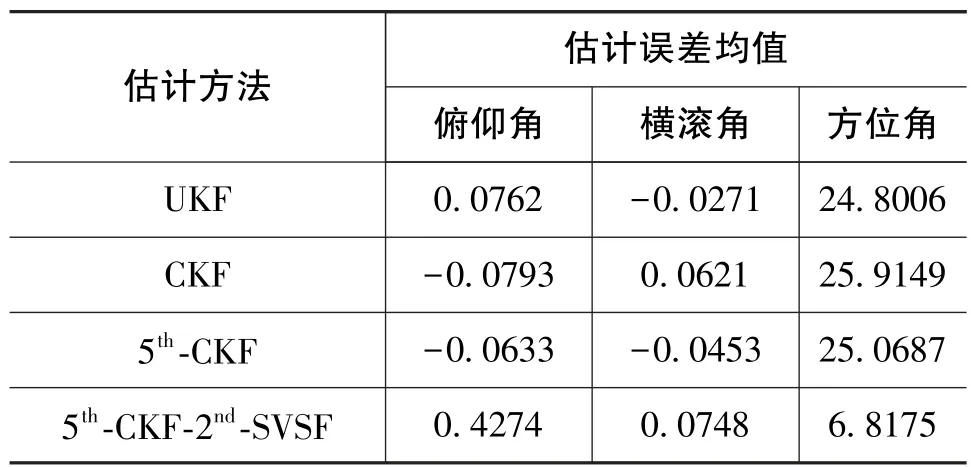
表2 估計誤差均值Table 2 Mean of estimation errors

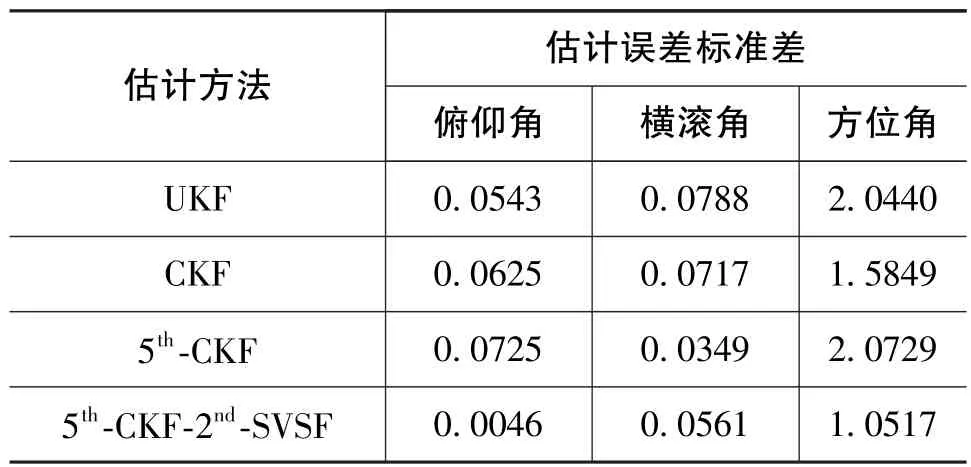
表3 估計誤差標準差Table 3 Standard deviation of estimation errors

從表2可以看出，五階容積-二階平滑變結構濾波方法的水平對準誤差不比其他方法的結果更好，但是其方位失準角估計精度明顯比其他幾種方法高。表3中的標準差表明了估計結果的穩定性，同時也說明了本文提出的方法具有更好的重現性。總之，五階容積-二階平滑變結構濾波方法能夠用于捷聯慣導初始對準過程中，并且能夠得到很好的估計精度和穩定的估計結果。

4 結論

本文提出了一種五階容積-二階平滑變結構濾波對準方法，該方法提高了大方位失準角對準過程中方位失準角的對準精度。五階容積-二階平滑變結構濾波方法需通過Kalman 濾波對準方法和羅經對準方法組合的方式才能得以實現。五階容積-二階平滑變結構濾波是一個魯棒估計方法，仿真結果表明該方法比其他常規對準方法有更好的估計精度。此外，需要特別指出的是，五階容積-二階平滑變結構濾波對系統構成還有其特殊要求，即系統狀態變量維數與量測變量維數要相同，且要求系統完全可觀和可控。本文通過組合對準方法和量測模型的切換，很好地解決了其在捷聯慣導系統初始對準中的應用這一問題。