股票市場的高維動態(tài)因子模型及其實證分析

鄭紅景，蔣夢夢，周 杰

西安電子科技大學 數(shù)學與統(tǒng)計學院，西安710126

1 引言

收益率和波動率是諸多經(jīng)濟和金融研究的重要方面。收益率反映了金融市場的價格波動，波動率則體現(xiàn)了價格波動的劇烈程度。收益率及其波動情況關系到證券組合的選擇和風險管理。現(xiàn)實中一些國內(nèi)政策及隨機性事件，如宏觀調(diào)控、市場突發(fā)事件等都會對股票市場產(chǎn)生影響。目前對這些因素的研究主要有主成分分析、線性回歸分析等，但這些方法僅能處理低維數(shù)據(jù)，尤其是線性回歸分析，只能分析特定因素對結果的影響，因此本文構建了動態(tài)因子模型（DFM）。動態(tài)因子模型可以從數(shù)據(jù)集中提取少量公共因子，來反映其對股票收益率和波動率的影響。

從現(xiàn)實情形看，科學技術不斷發(fā)展，政府統(tǒng)計的數(shù)據(jù)也在增多，由此帶來了處理高維數(shù)據(jù)的難題。動態(tài)因子模型是傳統(tǒng)因子模型在時間序列方面的推廣與發(fā)展，擅長處理觀測時間點個數(shù)大于觀測變量個數(shù)的數(shù)據(jù)[1-2]。若觀測變量維數(shù)較高，且因子的影響有限，觀測方程的因子載荷矩陣往往是稀疏陣。目前為止動態(tài)因子模型的估計方法有三種，一是狀態(tài)空間和極大似然估計法[3]，但它只能處理低維的動態(tài)因子模型。二是提取主成分法[4]，三是主成分和狀態(tài)空間的混合估計法[5]，后面兩者都不能得到稀疏的因子載荷矩陣。為解決以上問題，本文引入ERM（Expectation-Regularization-Maximization）算法[6]，利用ERM可得到高維動態(tài)因子模型的稀疏參數(shù)估計，而稀疏性也符合金融市場的實際情況。

將提出的模型及算法，應用到深滬交所的股票數(shù)據(jù)中，發(fā)現(xiàn)了收益率模型和波動率模型中都包含共同因子和行業(yè)因子，本文也分析了這些因子的波動趨勢及其原因。此外，還引入因子貢獻率來對比兩種因子對行業(yè)股票的影響程度。

2 動態(tài)因子模型

動態(tài)因子模型將n維可觀測變量yt描述成由幾個不可觀測的少量的公共因子xt和均值為0的特質(zhì)因子εt組成，其基本形式是：

其中，yt,εt∈Rn×1，動態(tài)因子的個數(shù)是q，所以xt,et∈Rq×1,t=1,2,…,T，滯后算子多項式矩陣λ(L)∈Rn×q，Ψ(L)∈Rq×q,L是滯后階數(shù)，假定Q和R均為對角陣。這里已對yt進行了標準化，去除截距項。

式（1）中模型在沒有任何約束的情況下是不可識別的，為使模型可識別[7-8]，加入以下約束條件：

（1）本文假定因子載荷矩陣λ(L)的滯后階數(shù)為1階，并記為C，且限定C的前q-1行，當i=1,2,…,q-1且j＞i時，Cij=0。

（2）Ψ(L)為單位陣。

此時，模型可以簡寫為狀態(tài)空間模型[9]的形式：

其中， x1～N(μ0,Σ0)。

通過對因子載荷矩陣C的估計，可以得到y(tǒng)t與隱含的公共因子xt的相關關系。若Cij≠0，代表在其他因素保持不變的前提下，股票的公共因子xt每增加一個單位，股票i的取值改變Cij個單位，若Cij=0，則此公共因子不影響股票i。

3 高維因子模型的參數(shù)估計

在模型中待估計的量為θ=(C,Q,R,μ0,Σ0)，核心問題是因子載荷矩陣C的估計。通常可以通過極大似然估計來計算θ，但在高維情況下，矩陣C是稀疏的，狀態(tài)空間和極大似然估計法只能處理維度較低的模型，提取主成分法和主成分與狀態(tài)空間的混合法都無法將C中極小的數(shù)值壓縮為0。因此，本文采用帶懲罰的EM算法（ERM），即在EM算法中加入正則項，以此得到矩陣C的稀疏估計。

ERM算法分三步：E步用卡爾曼濾波和光滑[10]來計算公共因子xt其統(tǒng)計量，并求出條件期望似然函數(shù)；R步利用正則化，得到因子載荷矩陣C的稀疏估計；M步極大化條件期望似然函數(shù)，得到其余未知參數(shù)Q,R,μ0,Σ0的估計，具體算法如下。

E步，動態(tài)因子模型的聯(lián)合似然函數(shù)為：

則其對數(shù)似然函數(shù)的條件期望為：

計算θr時用到的狀態(tài)變量及它的充分統(tǒng)計量有：

式（6）統(tǒng)計量可由卡爾曼濾波和光滑過程得到。

R步，利用自適應lasso[11]、彈性網(wǎng)[12]和自適應彈性網(wǎng)[13]實現(xiàn)正則化。

首先利用EM算法，通過最大化對數(shù)似然函數(shù)的條件期望來得到因子載荷矩陣C的不稀疏估計。即Ψ關于C求偏導，有：

令式（7）等于0，C的極大似然估計為：

然后通過極小化損失函數(shù)加正則項的方法，用LARS算法實現(xiàn)自適應lasso、彈性網(wǎng)和自適應彈性網(wǎng)估計，來得到稀疏的C。先將式（2a）寫成偽回歸形式，令：

這里 vec是拉直算子， ?表示Kronecker積。則偽回歸為：

最大化對數(shù)似然函數(shù)等價于極小化損失函數(shù)，帶懲罰的損失函數(shù)為：其中，λ是一個調(diào)優(yōu)參數(shù)，L(c)是正則項。自適應lasso對應的是，其中，彈性網(wǎng)對應的是，自適應彈性網(wǎng)對應的是

用LARS算法求解式（10），得到c的估計，然后將維數(shù)為nq×1的向量c變形為n×q維的矩陣C。隨著λ逐漸變大，C中的部分元素會逐漸被壓縮為0，當λ足夠大時，元素可能全部被縮小為0。因此，適當?shù)卮_定調(diào)優(yōu)參數(shù)λ是很重要的，本文采用的評估依據(jù)是擴展的貝葉斯信息準則（EBIC）[14]。

M步，用E步的充分統(tǒng)計量和R步得到的Cr-1，對條件期望似然函數(shù)關于Q,R,μ0,Σ0分別求偏導數(shù)，令偏導數(shù)等于0，得到這些參數(shù)的估計：

4 仿真實驗

本文共設定了三個仿真實驗，且采用三種不同的正則化方法實現(xiàn)估計：

實驗1 n=40,q=4,T=300，待估計的因子載荷矩陣C中元素有160個，非0元素占比p分別為10%、20%、30%。

實驗2 n=60,q=4,T=300，待估計的因子載荷矩陣C中元素有240個，非0元素占比p分別也是10%、20%、30%。

實驗3 n=60,q=4,T=500，待估計的因子載荷矩陣中C元素有240個，非0元素占比p分別也是10%、20%、30%。

三個實驗都設定Q=0.01?In×n,R=0.01?Iq×q。按照以上設計，用100個不同的因子載荷矩陣隨機產(chǎn)生100組數(shù)據(jù)，重復實驗。為了評價ERM算法的性能，計算了因子載荷矩陣C的假陽率（FP）和假陰率（FN），計算方法為：

表1 實驗1仿真結果(n=40,q=4,T=300)

表2 實驗2仿真結果(n=60,q=4,T=300)

表3 實驗3仿真結果(n=60,q=4,T=500)

（1）對比三種正則化方法，自適應彈性網(wǎng)的效果優(yōu)于自適應lasso和彈性網(wǎng)。

（2）對比表1和表2，在控制其他因素不變的前提下，當待估計的元素個數(shù)逐漸增加時，F(xiàn)P和FN都會略有增加。

（3）對比表2和表3，在控制其他因素不變的前提下，當觀測時間點個數(shù)增加時，F(xiàn)P和FN都有減少，這是因為當觀測數(shù)據(jù)增加時，包含的信息也會越來越準確。

5 股票市場收益率和波動率

本文隨機選取了深滬交所上市的120支股票（即A股）其中包含通信行業(yè)、制造業(yè)和互聯(lián)網(wǎng)行業(yè)各30支，其余30支為其他行業(yè)股票，數(shù)據(jù)為2018年1月2日到2018年12月28日（除節(jié)假日）的共242天的收盤價。

股票i的第t天收盤價為sit，對數(shù)收益率為yit=ln sitln si(t-1)。股票的歷史波動率[15]為由于n+1為股票價格時間區(qū)間，而本文計算的是日化波動率，則n=1，且對y已進行標準化處理，故hit=|yit|，此時hit全為正數(shù)，為使數(shù)據(jù)更好地服從正態(tài)分布，本文將收益率的平方取對數(shù)作為對數(shù)波動率git=。

5.1 股票收益率模型

在模型估計時，首先要確定公共因子個數(shù)，常用的方法有陡坡圖法[16]和IC信息準則法[17]等，但當因子相關性較高時陡坡圖法會造成重復。除此之外，由于因子載荷矩陣的稀疏性，經(jīng)IC信息準則法估計出的因子載荷矩陣的某一列可能全部為0，不符合所確定的因子個數(shù)，因此也不適用。為解決以上問題本文提出一種新的方法：預先給定不同的因子個數(shù)，根據(jù)估計的稀疏的因子載荷矩陣，直接得到公共因子的實際個數(shù)及實際的因子載荷矩陣。

先假定因子個數(shù)分別為q=5,8,9,由此得到了股票收益率模型的參數(shù)估計。雖然q個數(shù)不同，但因子載荷矩陣C中都只有3列元素有非0元素，且其對應元素位置和大小相似，因此實際上公共因子個數(shù)為3。此外因子載荷矩陣中元素絕大部分為正數(shù)，可知公共因子與大部分股票收益率呈正相關，即因子向上波動時對收益率有積極影響，反之有消極影響。

5.1.1 通信因子

由于因子載荷矩陣的稀疏性，表4列出的是因子載荷矩陣的第1列中前12支非0元素（按絕對值大小排序）及其對應的股票和所屬行業(yè)。

從表4可知這些股票大部分屬于通信行業(yè)，因此可將該公共因子歸結為通信因子。通信因子隨時間變化的線圖，如圖1。

圖1 通信因子隨時間變化線圖（收益率模型）

分析圖1，發(fā)現(xiàn)通信因子在年初、7到8月有小幅度的向上波動，5月因子也有明顯的向上波動。

結合政策因素分析，發(fā)現(xiàn)在通信行業(yè)，2月份發(fā)改委通知5G規(guī)模組網(wǎng)建設工作逐步展開，5月底，5G已經(jīng)完成第一階段全功能標準化工作，進入了沖刺新階段，7月到8月底，5G技術研發(fā)實驗第三階段逐步完成。由此說明了此因子與5G技術的研發(fā)有關。

5.1.2 共同因子

因子載荷矩陣的第2列元素大部分非0，表5列出的是前20個（按絕對值大小排序）的非0元素及其對應的股票和所屬行業(yè)。

由表5可知此公共因子對應的因子載荷矩陣中元素大部分非0，即對大部分股票都有影響，因此可稱其共同因子。共同因子隨時間變化的線圖，如圖2。

圖2 共同因子隨時間變換線圖（收益率模型）

由圖2可知共同因子在年初、3月下旬、6月15日左右、10月中旬都出現(xiàn)了明顯的向下波動，而10月下旬出現(xiàn)了向上波動的趨勢，其余時刻處于相對平穩(wěn)狀態(tài)。

究其原因，3月份美國推出多項針對中國的貿(mào)易措施，導致A股大幅下跌。6月份美國再度加息，同時對華貿(mào)易爭端升級，對國內(nèi)股市影響加大。而10月底，面對A股滬指的弱勢，央行、銀保監(jiān)會全力維穩(wěn)市場，同時也推出各項改革政策致力于穩(wěn)定我國股票市場。

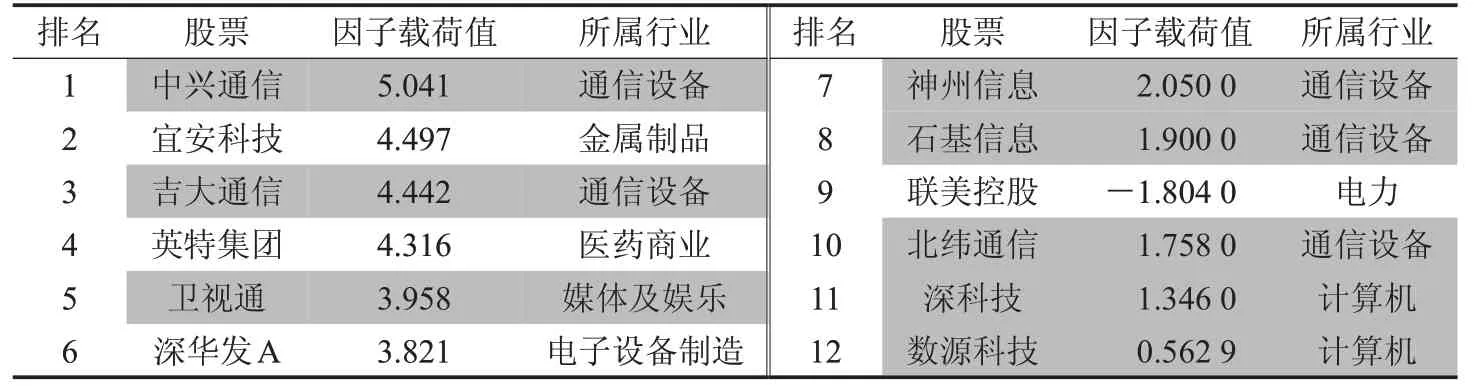
表4 通信因子影響的股票（收益率模型）

5.1.3 制造因子

表6是因子載荷矩陣的第4列中前12支非0元素（按絕對值大小排序）及其對應的股票和所屬行業(yè)。

從表6可以看出，這些股票大多是制造業(yè)，故將此公共因子歸為制造因子。制造因子隨時間變化線圖，如圖3所示。

圖3 制造因子隨時間變換線圖（收益率模型）

由圖3知，制造因子在6月中下旬有明顯向下波動的現(xiàn)象，而在10月下旬到11月初因子向上波動。結合當前形勢，這與中美貿(mào)易戰(zhàn)爭有關。6月份，美國加大了中國出口貨物的稅率。但在10月份，我國深入實施推進制造業(yè)建設解決深層次矛盾，對制造業(yè)產(chǎn)生了積極影響。

5.2 股票波動率模型

與收益率模型一樣，也假定因子個數(shù)分別為q=5,8,9,由此得到了股票波動率模型的參數(shù)估計，所有因子載荷矩陣C中都只有2列元素有非0元素，且其對應元素位置和大小相似，因此實際上公共因子個數(shù)為2。且因子載荷矩陣中元素絕大部分為正數(shù)，可知公共因子與大部分股票波動率呈正相關。

5.2.1 共同因子

因子載荷矩陣的第1列元素大部分非0，表7列出的是前20個的非0元素（按絕對值大小排序）及其對應的股票和所屬行業(yè)。

由表7可知此公共因子影響全國大部分股票，故稱其為共同因子。共同因子隨時間變化的線圖，如圖4。

表5 共同因子影響的股票（收益率模型）

表6 制造因子影響的股票（收益率模型）

表7 共同因子影響的股票（波動率模型）

圖4 共同因子隨時間變換線圖（波動率模型）

由圖4可知共同因子在1月下旬、5月底、10月中下旬都出現(xiàn)了明顯向下波動，其余時刻波動相對較小。

從政策方面看，1月金融監(jiān)管政策密集出臺，貨幣政策也致力于維持流動性穩(wěn)定，5月中美貿(mào)易關系日趨緊張，美國以貿(mào)易戰(zhàn)為突破口實施對華遏制戰(zhàn)略，旨在打擊我國對外貿(mào)易，10月份外圍氛圍爭端持續(xù)升級，國內(nèi)經(jīng)濟增長已然持續(xù)承壓。由此可見，中美貿(mào)易戰(zhàn)爭對我國金融市場產(chǎn)生了很多負面影響。

5.2.2 互聯(lián)網(wǎng)因子

表8是因子載荷矩陣的第3列中前12支非0元素（按絕對值大小排序）及其對應的股票和所屬行業(yè)。

表8中股票大多為互聯(lián)網(wǎng)行業(yè)，可將此公共因子歸為互聯(lián)網(wǎng)因子。互聯(lián)網(wǎng)因子隨時間變化的線圖，如圖5。

圖5可以看出，互聯(lián)網(wǎng)因子在2018年大多數(shù)時間都是呈現(xiàn)向上的波動，這與2018年人工智能領域的快速發(fā)展有關。因子在8月7日和11月中下旬有兩次明顯的波峰，這應該是與國家政策有關，8月有20多個省市發(fā)布相關文件和扶持政策，10月31日中共中央政治局進行的集體學習中，習總書記強調(diào)了人工智能發(fā)展的重要性。

圖5 互聯(lián)網(wǎng)因子隨時間變換線圖（波動率模型）

5.3 收益率模型和波動率模型的異同

5.3.1 公共因子類型異同

分析兩個模型的兩個共同因子，發(fā)現(xiàn)兩者波峰和波谷出現(xiàn)的時間和原因有相似之處，這是因為國內(nèi)金融市場的重大事件如中美貿(mào)易爭端和政府出臺的政策措施，對兩者均有影響。但其他因子只對二者之一產(chǎn)生影響，如在收益率模型中的通信因子只對通信行業(yè)的收益率產(chǎn)生了影響；而波動率模型中的互聯(lián)網(wǎng)因子只對互聯(lián)網(wǎng)領域的波動率有影響。

5.3.2 模型中各公共因子的貢獻率

由于共同因子影響大部分股票，而行業(yè)因子只影響某行業(yè)股票，為研究兩種因子對行業(yè)股票的影響程度，本文進一步利用方差分解的方法進行度量。基本原理是：計算每個行業(yè)因子和共同因子的方差vi占總方差的比例作為因子的貢獻率，即。具體結果見表9。

由表9可知，在收益率模型的通信行業(yè)和制造業(yè)，共同因子的貢獻率比行業(yè)因子的貢獻率略大，說明共同因子對股票收益率的影響要大于行業(yè)因子。但在波動率模型中互聯(lián)網(wǎng)行業(yè)的行業(yè)因子貢獻率要遠大于共同因子，也就是說股票波動率受行業(yè)因子的影響更大。

6 結束語

本文基于高維動態(tài)因子模型，建立了金融市場的收益率和波動率模型，引入ERM算法得到了稀疏的參數(shù)估計。通過對滬深交所股票市場的分析，兩個模型中都有一個因子影響大部分股票，為共同因子，而其他因子是只對部分行業(yè)股票有影響的行業(yè)因子。本文分析了這些因子產(chǎn)生波動趨勢，并給出了可能的解釋，此外，通過計算因子貢獻率，發(fā)現(xiàn)通信行業(yè)和制造業(yè)股票的收益率更易受共同因子的影響，而互聯(lián)網(wǎng)行業(yè)股票的波動率更易受行業(yè)因子的影響，這些發(fā)現(xiàn)為研究金融市場的收益與風險提供了新的視角。以上研究是對金融市場動態(tài)因子模型的初步探討，也可從其他方面進行研究，如分層動態(tài)因子模型，這些研究對理解金融市場的影響因素也有重要的意義。

表8 互聯(lián)網(wǎng)因子影響的股票（波動率模型）

表9 各因子方差及貢獻率