基于遞歸神經網絡的多機器人智能協同控制*

程韜波，李曉曉 ，徐智浩，周雪峰

（1.廣東省智能制造研究所，廣州 501070；2.廣東省現代控制技術重點實驗室，廣州 501070）

0 引言

機器人被譽為“制造業皇冠頂端的明珠”，是實現智能制造的重要載體[1]。近年來，隨著機器人技術的推廣應用，其操作要求越來越復雜化、精密化，單個機器人難以滿足當前柔性化生產的市場需求，主要表現在[2]：（1）單機器人負載能力有限、工作空間較小，難以適應大空間加工任務；（2）單機器人加工的作業效率有限；（3）單個機器人的自由度有限，難以滿足實現復雜度高的加工任務。多機器人協作系統具有高冗余自由度、結構靈活多變等特點，是解決上述問題的有效途徑之一。其中，多機協同控制指通過設計協同控制策略，使多機器人執行共同的任務，在多機搬運、裝配、焊接等領域應用廣泛[3-5]。

針對快速切換的加工任務，傳統示教或離線編程方式效率不足；實時運動控制工程意義較強，但同樣面臨技術挑戰：需要根據多機器人加工任務實時設計控制量，實現對給定任務軌跡的跟蹤，同時能夠實時避免機器人超越其關節約束。此外，區別于傳統單機控制，多機器人系統之間可能存在結構閉鏈，機器人之間的相互影響對系統的同步性有很高的要求。

針對上述挑戰，金龍等[6]利用遞歸神經網絡（RNN）的實時處理性能為雙機器人提出一種基于RNN的同步控制方案，但未提及機器人之間的通信方式。李帥等[7]提出一種樹形結構通信的多機器人協同控制方法，之后他們從博弈論的角度再次探討了該問題，提出一種分布式協同控制方案[8]。張海濤等[9]為實現機器人圓形編隊提出一種多機器人系統控制算法，通過使用排斥力/轉向力和相位調節機制，避免機器人之間或機器人與墻壁的碰撞。查延麟[10]結合量化通信和區間算術方法提出一種考慮系統不確定性的多移動機器人協調控制策略。陳梅等[11]提出一種隊形軌跡跟蹤控制方法，可使各機器人較快形成期望隊形，以期望隊形追蹤期望軌跡。Alessandro[12]提出一種分布式自適應控制策略，在機器人未知系統完整狀態的情況下實現協同控制。

上述多機器人協同控制策略大多基于系統狀態信息全局未知的情況，在設計控制方案時需要考慮期望軌跡信息獲取等因素。受益于5G通訊技術的發展，使得多機協同控制過程中可實時獲取各機器人的狀態信息，保證了集中式控制策略在工業多機器人的系統實現。機器人跟蹤控制問題通常分為兩類：關節空間跟蹤和任務空間跟蹤。關節空間跟蹤目標是設計一個控制器控制機器人的每一個關節去追蹤一條預定軌跡。任務空間跟蹤是在笛卡爾空間建立期望軌跡，將控制命令發送給關節的每個驅動器，然后控制末端執行器在笛卡爾空間執行。由于笛卡爾空間和關節空間之間映射關系的高度非線性，任務空間跟蹤比關節空間跟蹤更困難。

本文研究關節約束下多機器人任務空間跟蹤的智能協同控制問題，以軌跡追蹤為主要任務，首先構建同步跟蹤誤差并設計外環控制策略，選取關節速度范數最小化為次級任務，進一步考慮關節速度和關節角限幅，將多機協同運動控制問題建模為一個二次型優化問題，然后設計一個動態神經網絡控制器實時求解控制量，最后建立MATLAB與V-REP聯合仿真實驗平臺以驗證多機協同控制策略的有效性。

1 問題描述

1.1 機器人模型

機器人的正向運動學模型可以描述為：

式中：r(t)∈?n，為機械臂末端執行器t時刻在笛卡爾空間中位置和方向的n維向量；θ(t)∈?m，為關節空間中的m維向量，它的每一個元素表示一個關節角，不失一般性，本文考慮機器人存在冗余自由度的情況，即m＞n；f(·)為笛卡爾空間到關節空間映射關系的非線性函數，通常由機械臂的結構和參數決定。

對式 （1）求導可得速度層r˙(t)與 θ˙(t)的映射關系：

式 中 ： J(θ(t))=?f(θ(t))/?θ(t)∈?m×n， 為 雅 可 比 矩 陣 ；r˙(t)和θ˙(t)分別為機械臂末端執行器的笛卡爾速度與關節角速度。

由于f(·)的非線性和冗余性，給定期望軌跡r(t)→rd(t)很難獲得相應的關節角θ(t)。式（2）速度層從關節空間到笛卡爾空間的映射簡化了該問題。

1.2 控制目標

本文研究多機器人任務空間跟蹤的智能協同控制問題，考慮機械臂關節角和關節速度限幅，定義第i個機械臂的關節角 θi和角速度的上下界分別為，期望軌跡為rd(t)，各機器人相對其初始位置的位移為ri(t)-ri(0)，i=1,2,…,N。智能協同控制的目標可以描述為：設計關節速度指令使機器人協同完成軌跡追蹤任務且不發生相對位移，即r1(t)-r1(0)=…=rN(t)-rN(0)=rd(t)-rd(0)。

2 協同控制器設計

2.1 二次型問題描述

機器人逆運動學指給定笛卡爾空間期望速度r˙(t)和機器人模型雅可比矩陣J(·)已知情況下計算機器人對應位置的關節速度θ˙(t)。偽逆法求解機器人逆運動學相對簡單，然而該方案未考慮機器人關節約束。由于機器人的物理結構和機械臂關節通常由一個伺服電機驅動，關節旋轉角度和關節角速度有限。如果違反關節限幅，機器人協同追蹤將會產生大追蹤誤差或造成對機械臂的損害甚至是協同追蹤任務失敗。由于m＞n，冗余機械臂的逆運動學解不唯一，機械臂冗余的性質可以使得根據某些特定的優化標準（如關節速度范數最小化、重復性優化、關節加速度范數最小化等）和約束條件（關節角、關節速度或關節加速度約束）在所有可行解中選擇最優的一個。

基于約束優化思想，將機械臂的物理約束抽象為不等式約束，機械臂末端執行器笛卡爾空間到關節空間的非線性映射抽象為等式約束，優化目標函數選擇關節速度范數最小化，將多機器人協同運動控制問題建模為一個二次型問題如下：

為提高機器人之間的同步精度，設計一個同步機制并將式（4）改寫為：

如果期望機器人末端執行器以速度r˙i運動，式（4）描述了機器人關節角速度θ˙i需要滿足的條件，同時也是系統協同跟蹤誤差收斂到零的充分必要條件。由于約束式（5）和式（6）描述在不同層，很難直接求解該二次型問題。因此利用速度逃逸法[13]將式（5）和式（6）共同描述在速度層，得到：

2.2 RNN控制器

對于上述得到的速度范數最小化約束優化問題，定義拉格朗日函數為：

式中： NΩi(θ˙i)為集合 Ωi在 θ˙i處的正規錐。

式（12）可以進一步描述為：

式中：PΩi為投影算子。

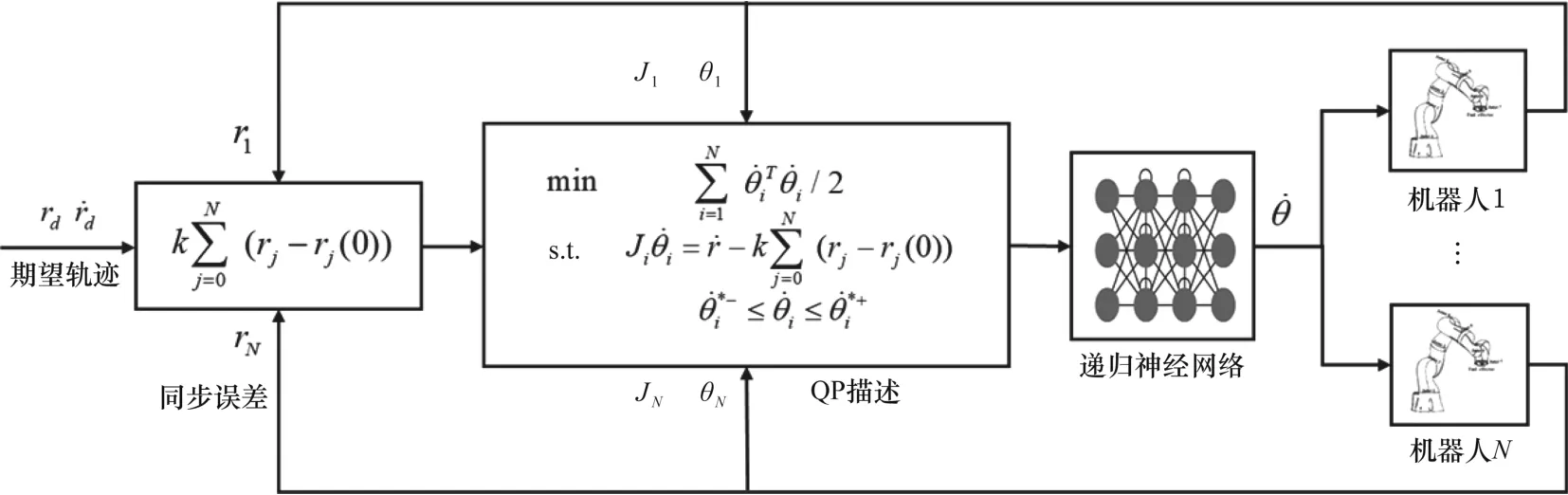
圖1 基于RNN的多機器人協同控制框圖

由于多機器人系統的非線性性質，式（8）具有高度非線性的特點，目前尚沒有可以直接求解式（8）的解析方法，而且利用數值算法求解的效率很低且功能有限，利用RNN并行計算性能優化的特點，本文設計了RNN神經動態求解器求解：

式中：ε＞0為正常數。

基于RNN的多機器人智能協同控制框圖如圖1所示。

綜上所述，基于RNN的多機器人系統協同控制問題可歸納為三步：（1）建立同步誤差，選擇優化目標函數并將機械臂協同控制問題建模為約束二次型優化問題（見式（8）～（10））；（2）在對偶空間中研究該問題，以非線性方程的形式建立其解表達式（見式（16）～（17））；（3）設計一個收斂的神經動力學系統，其穩態解與非線性方程組的穩態解相同（見式（16）～（17））。

3 仿真實驗

為驗證所提協同控制方案的有效性，本文建立了MATLAB+V-REP[14]聯合仿真實驗平臺。以圖2所示的7自由度iiwa R800機械臂為對象，機器人個數為3，期望運動軌跡設定為三環路徑：

式中： μ=πt/T，實驗設置中T=10；參數lx，ly和lz分別設置為-0.191 5，0.511 0和0.656 0。神經網絡參數ε1=…=ε3=0.000 5。3個機器人的關節角初始值θ（0）分別設置為[0 , 20,0,-60,0,30,0]T·π/180°rad ，[0,20,0,-60,0,30,0]T·π/180°rad， [0,-20,0,60,0,-30,0]T·π/180°rad 。控制增益參數設置為k=1，α=8。關節角和關節速度的上下限分別為=-1.5 ，-0.7。仿真實驗中本文僅考慮了3D空間中的位置控制，表1所示為iiwa R800機械臂的DH參數。

表1 DH參數表

圖2 7自由度iiwa R800機械臂模型

圖3 對三環曲線的協同控制結果

實驗結果如圖3、4所示。圖3（a）所示為軌跡誤差曲線，末端執行器位置誤差通過計算e=r-rd∈?3獲得，基于所設計的控制器，機器人實現的軌跡與期望軌跡之間的誤差可達到10-4量級。圖3（b）～（d）分別為λ，關節角θ和關節速度的曲線圖。在t=8時關節速度θ達到了最大值（±1.3 rad），在t=1和t=5時關節速度達到了最大值（±0.4 rad/s），但是關節角和關節速度皆在所設置的約束范圍之內，并且在協同控制方案的控制下，曲線都比較平滑，處于一個相對平穩的狀態。圖4（a）所示為三環曲線跟蹤過程中V-REP環境下截取的跟蹤效果，圖4（b）所示為最終狀態下機器人實現的曲線跟蹤結果，可以看到在神經網絡協同控制器控制下所有機器人最終都精確實現了期望的三環路徑軌跡。

圖4 V-REP環境下對三環曲線的跟蹤效果

4 結束語

本文針對多機械臂協同運動控制問題提出了一種基于RNN的協同控制方案。機器人關節角和關節角速度限幅描述為不等式約束，設計了一個動態RNN控制器實時控制機器人的運動。MATLAB與V-REP聯合仿真實驗驗證了在神經網絡協同控制策略的控制下，多機器人系統成功地實現了期望軌跡跟蹤，跟蹤誤差可達到10-4量級，且關節角和關節速度值都在所設置的限幅內。

對多機器人系統而言，障礙物避免方案不僅要考慮機器人與環境的碰撞，還要考慮機器人之間的碰撞，這是一個值得探討且充滿挑戰的問題。未來工作將致力于多機器人系統障礙物避免策略研究。