基于兩種本構模型的堆石壩應力變形比較研究

朱俊高，單一峰*，鄭惠峰，劉 忠

(1.河海大學 巖土力學與堤壩工程教育部重點實驗室，江蘇 南京 210098；2.河海大學 巖土工程科學研究所，江蘇 南京 210098；3.中國電建集團華東勘測設計研究院有限公司，浙江 杭州 330110；4.黃河水利委員會黃河水利科學研究院，河南 鄭州 450003)

近年來，隨著堆石壩筑壩高度的增加，有限元分析在壩體設計中起到了不可或缺的作用。有限元計算對選取的本構模型及其模型參數具有較大的依賴性，不同的本構模型在計算堆石壩的應力變形時，計算結果相差較大[1-3]。因此，在有限元計算中，本構模型的合理選取至關重要。在我國堆石壩的有限元分析中，彈性非線性模型(如鄧肯模型、K-G模型)和彈塑性模型(如南水模型、橢圓-拋物雙屈服面模型)都得到了不同程度的應用。鄧肯E-B模型[4]，參數確定簡單，模型參數的物理意義明確，為彈性非線性模型的代表模型，被廣泛應用于堆石壩的有限元分析中[5-7]，但該模型基于廣義胡克定律，不能反映剪脹性。殷宗澤提出的橢圓-拋物雙屈服面彈塑性模型[8]，綜合了單屈服面模型的優點，能較好反映土的剪縮剪脹性及復雜應力路徑對土體變形的影響，具有較好的實用性。

目前，已有學者比較了這幾類模型在有限元計算中的差異[9-10]，如趙曉龍[11]等比較了鄧肯-張模型和橢圓-拋物雙屈服面模型土石壩應力變形的計算結果。朱俊高[12]等人結合糯扎渡心墻壩實例，分析比較了鄧肯-張模型和鄧肯E-B模型在有限元計算中的差異。結果表明使用不同模型計算所得到的壩體變形和應力分布均有所區別。盡管上述研究對比眾多，但少有學者對鄧肯E-B模型和橢圓-拋物雙屈服面模型計算的堆石壩應力變形進行全面的分析比較。基于此，本文以兩岔河心墻堆石壩為例，分別采用鄧肯E-B模型與橢圓-拋物雙屈服面模型進行三維有限元計算，并對計算結果進行了對比分析，探究兩種模型在應力和變形的差異，為心墻堆石壩有限元計算本構模型的選取提供了參考依據。

1 工程概況和有限元模型

兩岔河水庫位于四川省涼山州會東縣。擋水建筑物為粘土心墻堆石壩，壩頂長度247.00 m，寬10 m，最大壩高74.50 m。心墻頂寬4.0 m，上、下游坡比1∶0.25，心墻最大底寬39.25 m，心墻與兩岸壩肩混凝土墊層接觸部位采用厚度2.0 m的高塑性粘土過渡。壩基覆蓋層防滲采用一道混凝土防滲墻，墻厚1.2 m。防滲墻頂通過廊道與防滲心墻連接，底部嵌入基巖。壩體分區見圖1。

壩體各分區的鄧肯E-B模型和橢圓-拋物雙屈服面模型的計算參數分別見表1和表2。其中鄧肯E-B模型參數通過常規三軸試驗確定，雙屈服面模型參數通過河海大學巖土所研制程序[13]由E-B模型參數轉換得到，具體如下：由已知E-B模型參數計算出對應土石料應力應變曲線族，再用最優化方法擬合，從而獲得橢圓-拋物雙屈服面模型參數。

大壩共劃分59 480個結點、56 848個單元。單元網格劃分時，對土石料、混凝土等單元，大部分用8結點6面體單元，少數用6結點5面體、4結點4面體等單元過渡，邊界條件設置為底面xy雙向約束，壩體兩岸yz雙向約束，同時采用接觸面單元模擬各種材料邊界力與變形的協調關系。為了更好地模擬現場實際工程情況，計算采用分級加荷對大壩逐級施工及蓄水過程進行有限元計算，分19級進行加載，其中前15級為施工加荷，后4級為蓄水加荷，不考慮滲流的影響，僅作為附加水荷載。大壩三維有限元網格見圖2，河谷段最大斷面網格見圖3。

表1 鄧肯E-B模型計算參數Tab.1 Parameters of Duncan E-B model

表2 橢圓-拋物雙屈服面模型計算參數Tab.2 Parameters of ellipse-parabolic double yield surface model

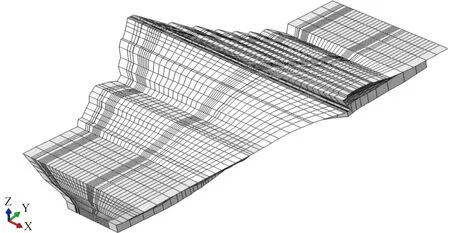
圖2 大壩三維有限元網格Fig.2 Three-dimension finite element mesh

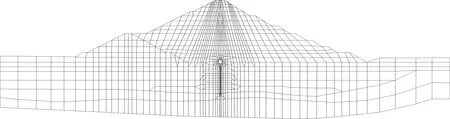
圖3 河谷段最大斷面網格Fig.3 The maximum cross section of valley segment

2 有限元計算結果及分析比較

本文采用河海大學巖土工程研究所研制的TDAD三維有限元軟件，進行兩種不同本構模型的應力變形計算，計算整理得到的最大沉降和水平位移見表3。為研究應力變形分布規律，整理出了(正常高水位)滿蓄期壩體及防滲墻的沉降和順河向水平位移等值線，見圖4—圖7，以及滿蓄期大主應力和小主應力等值線，見圖8—圖11。

2.1 壩體位移分析

由表3可知，鄧肯E-B模型和雙屈服面模型計算的最大沉降量很接近，雙屈服面模型計算的上下游水平位移小于鄧肯E-B模型計算結果，壩軸向整體水平位移(左右岸位移之和)較鄧肯E-B模型也偏小。總體上，兩種模型的沉降差異很小，水平位移差異稍大。說明了兩種模型在反映土石料性質能力上存在差異。

表3 滿蓄期壩體沉降位移結果Tab.3 Settlement and displacement of dam after water storage

注：表中正值代表位移指向壩體下游或沿壩軸指向右岸，負值代表位移指向壩體上游或沿壩軸指向左岸。

圖4給出了滿蓄期壩體沉降等值線，可以看出，兩種模型計算的等值線圖分布規律基本相似，壩體沉降分布呈對稱形狀。總體上壩體沉降不大，壩體最大沉降在同一區域，位于心墻自底向上約1/3壩高處中心位置。滿蓄期兩種模型計算的最大沉降量分別是113.6、116.2 cm，分別占最大壩高119.5 m(含覆蓋層)的0.95%和0.97%。

經收集各大壩體的實際沉降數據資料發現[14]，一般情況下，滿蓄期的堆石壩最大沉降值約為壩高的0.52%～1.36%，最大位移比為0.029～0.749，鄧肯E-B模型和雙屈服面模型計算的位移比分別是0.294與0.240，均在合理范圍內。同時需要注意的是，在使用鄧肯E-B模型進行有限元計算的過程中，若泊松比μ大于0.5，勁度矩陣發生異常，無法進行下一步計算，因此該模型不能反映土體的剪脹性，并且，該模型也無法反映土體壓縮及剪切變形的交叉影響。綜上，使用可以反映剪脹性的雙屈服面模型進行有限元計算所得到的應力變形結果在理論上更加合理。

從圖4還可以看出，廊道與高塑性黏土區內的等值線分布比較密集，說明此處沉降梯度較大，這是由于廊道及防滲墻的支撐頂托作用導致該處產生較大的剪切變形。從沉降等值線圖還可以看出，覆蓋層的沉降等值線分布較為稀疏，相比于壩體沉降并不大。

圖5給出了滿蓄期壩體順河向水平位移等值線，其中，正值表示向下游位移，負值表示向上游位移。可以看出兩個模型計算的水平位移分布規律相近，由于土體自重作用，壩體在沉降的同時會產生向上下游的水平位移，但蓄水后由于水壓力向下游最大水平位移都明顯大于向上游的位移，蓄水后壩體向上游的最大水平位移位于靠近原地面線的上游壩殼內。滿蓄期壩體向下游的最大位移，用鄧肯E-B模型計算為30.2 cm，用雙屈服面模型計算為27.9 cm；滿蓄期壩體向上游的最大位移，用鄧肯E-B模型計算為9.3 cm，用雙屈服面模型計算為7.1 cm。相比鄧肯E-B模型，雙屈服面模型計算的上下游最大位移均更靠近中軸線。

圖6、圖7分別給出了滿蓄期防滲墻的沉降等值線和滿蓄期順河向水平位移等值線。圖中可見，防滲墻在河谷中央頂部沉降最大，往左右兩邊及底部逐漸減小，鄧肯E-B模型和雙屈服面模型計算的最大沉降分別為1.8和2.4 cm，雙屈服面模型計算的沉降較大，等值線變化梯度更大。蓄水后，防滲墻受覆蓋層土體側向擠壓均表現為向下游的位移，呈凹向上游變形。防滲墻最大水平位移位于近河谷中央的位置，往左右兩岸、頂部及底部位移逐漸減小。比較兩種模型計算結果，鄧肯E-B模型計算結果稍大，最大順河向水平位移為5.8 cm。

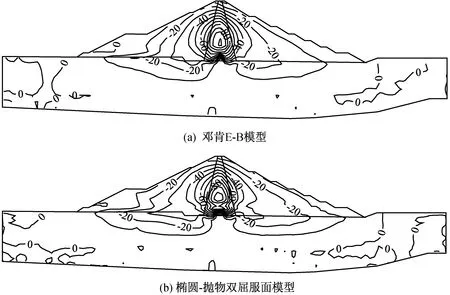
圖4 滿蓄期沉降等值線圖(單位：cm)Fig.4 Contour lines of settlement after water storage

圖5 滿蓄期順河向水平位移等值線(單位：cm)Fig.5 Contour lines of horizontal displacement along the river after water storage

圖6 滿蓄期防滲墻沉降等值線(單位：cm)Fig.6 Contour lines of settlement of cutoff wall after water storage

圖7 滿蓄期防滲墻順河向水平位移等值線(單位：cm)Fig.7 Contour lines of horizontal displacement along the river of cutoff wall after water storage

2.2 壩體應力分析

圖8給出了滿蓄期壩體典型橫斷面大主應力等值線。無論鄧肯E-B模型還是雙屈服面模型，滿蓄期壩殼內大主應力的等值線分布基本平行于壩坡，由外向內大主應力逐漸增加。受拱效應的影響，心墻內大主應力等值線比過渡層的大應力等值線更為稀疏[15]，尤其在心墻的中上部更為顯著。在心墻下部由于心墻及高塑性粘土受到下部廊道及防滲墻的頂托作用，心墻向下的沉降受到影響，使得這種拱效應作用下降，因此在心墻下部，心墻內大主應力較過渡層降低不明顯。由于雙屈服面模型考慮了塑性變形，能較為全面地反映土體的剪脹剪縮性及剪切變形的交叉影響，該模型下計算得到的壩體應力分布比較合理。

壩體典型橫斷面蓄水工況下的小主應力等值線見圖9。圖中可見，小主應力在壩體內的分布也近似呈平行于壩坡的形式，由外向內逐漸增加。由于拱效應，心墻內小主應力與過渡層的應力相比數值也有所下降，但與大主應力相比拱效應作用不明顯。鄧肯E-B模型計算的壩殼小主應力相比雙屈服面模型的結果降低得更為顯著。上游壩殼的小主應力由于蓄水影響明顯減小，心墻內靠近上游側小主應力也有所減小，但仍為正值(此處正值代表壓應力，負值代表拉應力)，說明心墻內并未出現拉應力。

對河谷段設有廊道和防滲墻的大壩，由于蓄水時在廊道和防滲墻上下游面存在水頭差，廊道和防滲墻將產生向下游順河向水平位移，而廊道兩端和防滲墻周邊受到基巖的約束，有可能在防滲墻和廊道部分區域產生拉應力，故需要特別關注。圖10給出了滿蓄期防滲墻中線處大主應力等值線圖，可以看出，大主應力等值線基本呈對稱分布，由防滲墻頂往左右兩邊及底部逐漸減小。大主應力均為壓力，防滲墻墻頂中部區域應力值最大，鄧肯E-B模型和雙屈服面模型計算值分別為15.5和20.5 MPa。

圖11為滿蓄期防滲墻中軸面小主應力等值線，由于受到周邊基巖的約束作用，小主應力在左右岸坡邊角部出現一定的拉應力。鄧肯E-B模型和雙屈服面模型計算的拉應力值分別為1.56和1.89 MPa。雙屈服面模型計算的拉應力的值及變化梯度均大于鄧肯E-B模型，且左岸拉應力差異較右岸更為明顯。

圖8 滿蓄期大主應力等值線圖(單位：MPa)Fig.8 Contour lines of major principal stress after water storage

圖9 滿蓄期小主應力等值線圖(單位：MPa)Fig.9 Contour lines of minor principal stress after water storage

圖11 滿蓄期防滲墻中線處小主應力等值線圖(單位：MPa)Fig.11 Contour lines of minor principal stress at the midline of cutoff wall after water storage

由大小主應力等值線圖可以看出，兩種模型計算的應力差異較大，故整理了截斷面中軸線的應力計算結果，對應力作進一步分析比較。圖12給出了心墻與防滲墻在最大斷面中軸線位置上的豎向應力σz和順河向應力σy的分布，可以看出，雙屈服面計算的應力均比E-B模型結果大。這是由于雙屈服面模型計算的沉降值大，而水平位移又較小，壩體材料擠壓效果更明顯。對于心墻部分，其雙屈服面模型計算的內部應力越大，對其防滲效果的發揮更好，如果心墻內應力太低，則可能產生心墻裂縫，甚至水力劈裂。對防滲墻，雙屈服面模型計算的應力比E-B模型的結果要大5 MPa左右，盡管都沒有超過C30混凝土強度，但對于高壩或更深厚的覆蓋層，還是應該引起注意，E-B模型計算的防滲墻應力可能偏小。

3 結論

1)鄧肯E-B模型與橢圓-拋物雙屈服面模型，兩種模型計算的壩體沉降十分接近，壩體水平位移有所差異。與雙屈服面模型相比，鄧肯E-B模型計算的上下游水平位移稍大，其壩軸向水平位移也比雙屈服面模型計算結果大。鄧肯E-B模型與雙屈服面模型計算的最大沉降分別占最大壩高(含覆蓋層)的0.95%和0.97%，位移比分別是0.294和0.240，與多個堆石壩工程監測數據比較，兩種模型計算的結果均符合實際工程沉降規律。

圖12 滿蓄期河谷中心壩軸線位置應力分布對比(單位：MPa)Fig.12 Stress comparison diagram of dam body truncated surface during full storage period

2)對于兩種模型計算得到的大小主應力，鄧肯E-B模型受拱效應的影響較為明顯，相同高程下，心墻內的大小主應力比過渡層的應力下降得更為明顯。心墻內的小主應力均為正，心墻處于受壓狀態。

3)雙屈服面模型計算的沉降較大，水平位移較小，使得壩體側向擠壓效果比鄧肯E-B模型更明顯，導致防滲墻大小主應力及應力變化梯度均大于鄧肯E-B模型。受周邊基巖的約束作用，防滲墻中軸面小主應力在左右岸坡區域均出現拉應力。兩種模型計算的防滲墻應力都在其混凝土的容許應力范圍內，其中左岸拉應力差異較為明顯，雙屈服面模型計算的拉應力的值及變化梯度較鄧肯E-B模型大。

鄧肯E-B模型和橢圓-拋物雙屈服面模型計算的心墻及防滲墻處的應力變形有明顯差異，可供設計綜合參考。基于雙屈服面模型能反映土體壓縮及剪切變形的交叉影響，且采用其計算結果設計更為保守。綜合考慮，在滿蓄期工況條件下，采用雙屈服面模型進行有限元計算更加合理準確。本文研究成果可為類似工程設計時的模型選用提供一定的參考依據。