基于流固耦合法的儲罐地震響應分析

翁 羽， 鄧志安，劉佳倫，潘 杰，吳 剛

(西安石油大學，陜西 西安 710065)

0 引言

早在上世紀中期，研究者就開展了剛性儲液罐的液體晃動研究。Housner[1]提出了基于剛性罐壁假設的儲液罐晃動流體域固體耦合問題的質量-彈簧系統的簡化模型。Haroun[2]使用彈性殼單元模擬罐體，流體部分使用附加質量法，從而獲得了改進的儲液罐地震響應分析方法。Broc等[3]使用ALE(Arbitrary Lagrangian Eulerian)描述法與有限元法結合，來求解瞬態流固耦合問題。Amabili等[4-5]針對該問題使用勢函數分解法進行分析，假設液體為理想流體、儲液罐為剛性。國內也有學者使用不同方法進行相關研究[6-8]。在能源領域，Sigrist等[9-10]使用均質模型來考慮流體及結構間的相互耦合作用，并成功將該方法用于各類承壓容器。

本文旨在使用CFD和FEM交替耦合的數值分析方法研究儲罐在地震條件下的內部流體晃動和結構響應特性，分析中考慮更為真實的氣液兩相黏性湍流態流體與結構之間的相互作用。

1 研究方法

1.1 研究模型

本文研究的儲罐采用臥式布置，設計運行壓力為0.3 MPa，本分析選取容器典型液體裝量(50%裝液量)作為分析條件。容器剖開示意圖如圖1所示。

對于結構計算模型和流動計算模型，網格剖分根據不同離散方法分別生成，分別使用四邊形殼單元和六面體單元進行網格劃分，其中FEM模型網格數量為60 000，CFD模型網格數量為3 790 000。儲罐計算網格模型如圖2所示。

1.2 數值計算方法

本文使用交替法由流體CFD程序和固體FEM程序分別在獨立的控制區域求解[11-13]，兩者分別用于計算兩相流體瞬態運動和固體結構瞬態變形。流固耦合的流程如圖3所示，CFD和FEM計算的數值模型選取如表1和表2所示。

圖1 儲罐結構示意圖

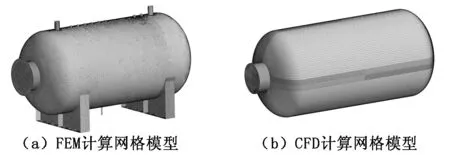
圖2 儲罐計算網格模型

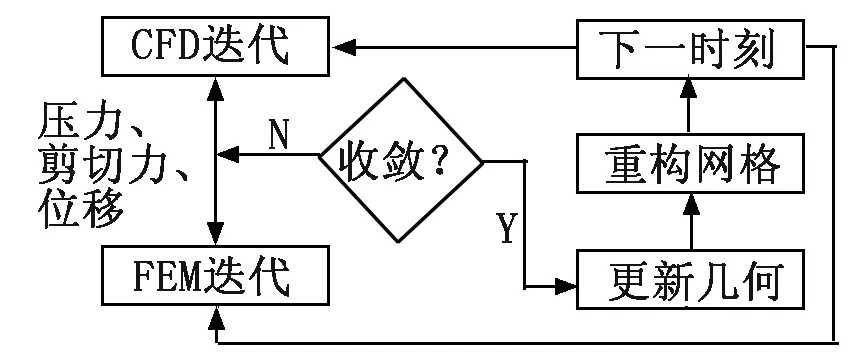
圖3 流固耦合流程示意圖

在計算中，CFD多相流控制方程主要包含質量守恒和動量守恒方程：

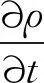
(1)

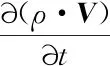
(2)

其中：ρ為密度；t為時間；為微分Hamilton算子；V為速度矢量；P為壓力；S為質量源項；μ為黏度；T為溫度；g為重力加速度；Tσ為相界面上的表面張力。各物理量為混合相參量。

FEM計算中主要控制方程為：

[B]=[φ][N].

(3)

{ε}=[B][D].

(4)

{σ}=E{ε}.

(5)

其中：[B]為單元應變矩陣；[φ]為四維(時間、空間)梯度矩陣；[N]為單元形狀函數；{ε}為應變向量；[D]為節點位移矩陣；{σ}為應力向量；E為彈性模量。

表1 CFD數值計算模型選取

表2 FEM數值計算模型選取

1.3 計算條件

本研究并不需要考慮流體的化學屬性，因此近似將流體介質考慮為熱工物性接近的純凈物，其中液相為不可壓縮流體，氣相為理想氣體。本研究選取當地基準地震譜的典型時程數據進行計算，計算選取10 s時長。地震加速度時程曲線如圖4所示。

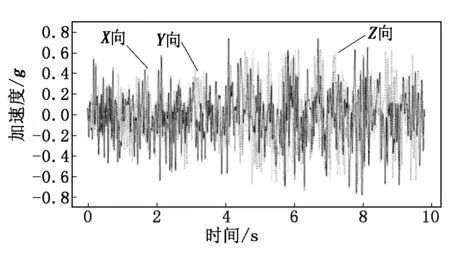
圖4 地震譜時程曲線

2 結果及分析

2.1 耦合法計算結果

分析得到的容器壁位移分布如圖5所示，容器內自由液面分布如圖6所示。由于地震加速度在初始一段時間內幅值較小，直接造成的容器及其支承結構的變形量并不大，從而導致的流體晃動不明顯，如圖5、圖6中(a)和(b)所示。當時間達到5 s時，液體晃動幅值顯著增大；對于容器結構響應，位移量顯著增大；這一階段的結構響應增加主要是由于液體晃動作用導致，如圖6(c)所示；圖5(c)中容器位移的高、低頻位移脈動同時出現的特性也是該現象的體現。在7 s之后，圖5(d)中“波浪”在上升至容器最高點后開始有液體團垂直落入液體自由表面。圖7為波浪高度變化情況，在7 s后的波谷變化反而不如5 s左右時劇烈。

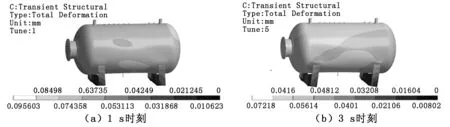
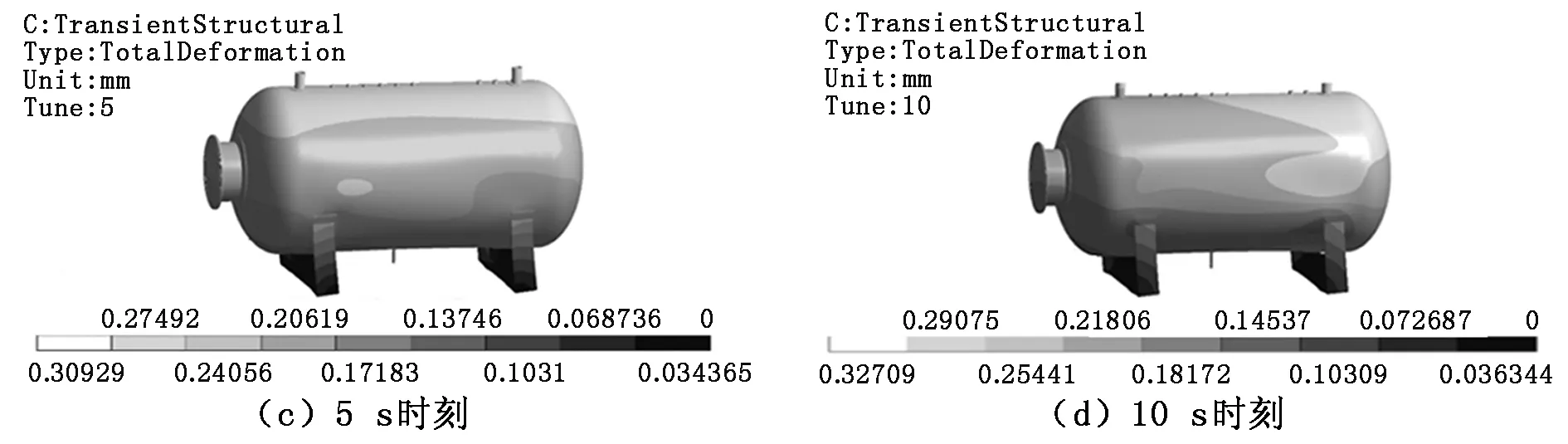
圖5 容器壁位移分布圖

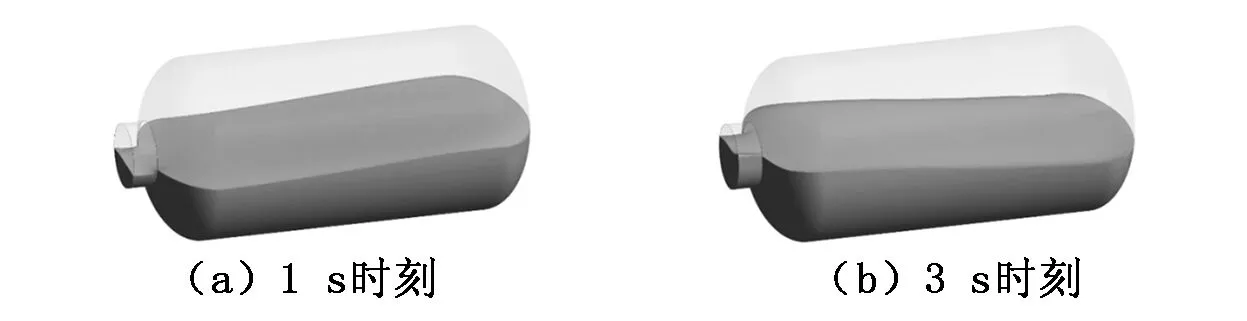
圖6 容器內自由液面分布圖

2.2 耦合法與附加質量法比較

為了比較本文所用的耦合法和傳統的流體附加質量法之間的差異，使用附加質量法重新計算。在容器下半部分內壁面上施加隨液體深度變化的質量。

圖8為兩種方法下的容器筒體部分最大位移時程。由圖8可知：附加質量法在地震開始階段獲得的位移量很大，遠高于耦合法，耦合法在地震中后期的位移量顯著大于附加質量法，由此可以得到液體的晃動將對結構響應產生很大的影響。圖9所示的容器筒體最大應力也與位移規律相同。

綜上，由于液體晃動所導致的結構響應非常重要，在總體結構響應中為主要因素，因此在分析本問題時，應重點考慮液體的晃動影響。

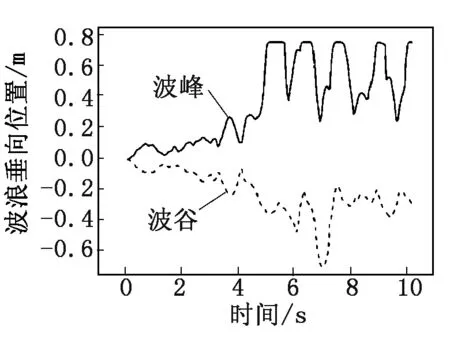
圖7 液面波浪高度隨時間分布圖

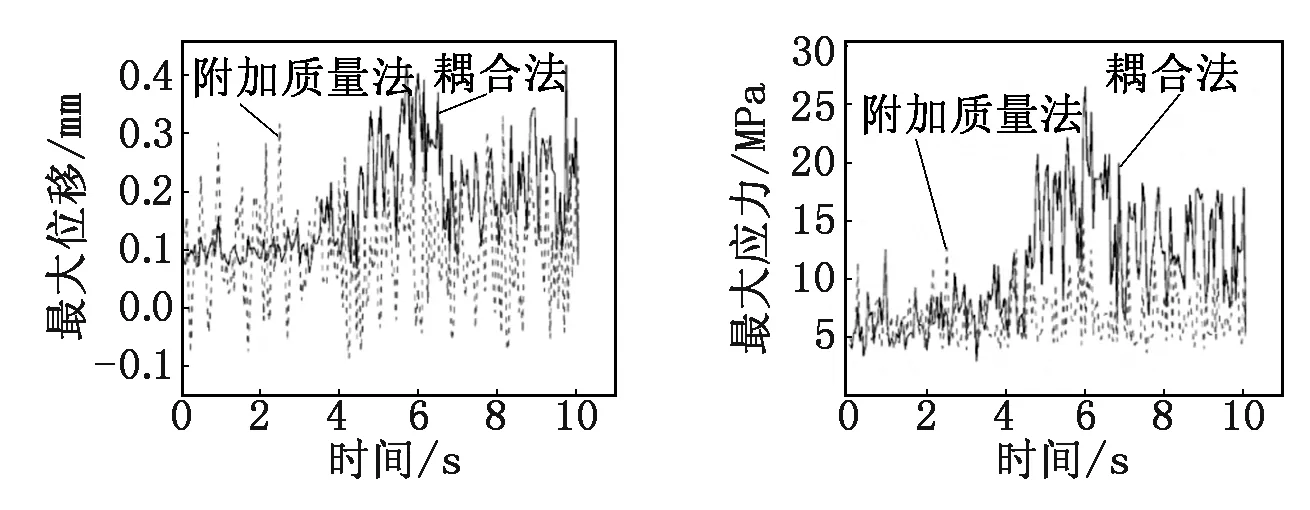
圖8 兩種方法容器壁最大位移隨時間分布圖 圖9 兩種方法容器壁最大應力隨時間分布圖

3 結論

經過上述分析，最終得到下列關于儲罐地震響應分析的結論：

(1) 使用CFD程序來直接對持續震蕩流動區域內的氣液兩相黏性湍流態流體進行計算可以捕捉到液體自由表面的詳細動態變化形式，進而通過流固耦合的方式獲得其對結構的影響特性。

(2) 在典型地震時程作用下，容器內液體自由表面的“波浪”高度逐漸增大，最終波峰和波谷維持在一定范圍內。

(3) 在典型地震時程作用下，容器結構的響應(位移、應力、支反力等)由初始的小幅振動發展為高幅值振動，隨著流固相互作用的充分發展，容器響應受液體晃動主導。

(4) 通過與附加質量法比較，判斷在本文所研究問題中，液體晃動所導致的結構響應非常重要。在液體和結構的相互作用下，結構響應遠大于僅考慮液體的剛性質量的情況，且響應的時域變化也受液體晃動影響巨大。因此在分析相似問題時，應重點考慮液體的晃動影響。